命题实践促进教师专业发展——从一道圆锥曲线解答题的原创历程谈起

广东 潘敬贞 杜龙安

教学考试杂志社主办的“优师计划”以“互联网+”为依托，创新教研模式，整合优质教育资源，共享优质教研成果，促进教师专业发展.笔者有幸参加了“优师计划”方向五“二轮知识体系巩固与测评”项目，收获颇多.本文主要谈笔者在本次项目研发中的一道圆锥曲线解答题的原创历程，与同行分享、交流.

一、试题命制过程

原创试题是以知识为载体、能力为导向、素养为落脚点，因此原创一道试题首先要确定考查内容与知识、考查能力与素养；然后选择合适的试题素材服务于能力与素养的考查；最后全面考虑试题主要考查目标方向、试题区分度，设置合适的问题.

1.考查内容

解析几何是高中数学教学的重点和难点内容.在考题中圆锥曲线解答题常以中档题或压轴题的形式出现，考查用代数方法解决几何问题，主要考查圆锥曲线的定义、方程、性质，还涉及平面几何的性质、韦达定理、直线方程、点到直线的距离公式、分类讨论思想和方程思想等解析几何核心内容.

2.考查能力和素养

因为圆锥曲线解答题主要以中档题或压轴题的形式出现，试题的解答对学生的能力要求比较高.主要考查学生的推理论证能力、运算求解能力、分析问题与解决问题的能力，考查学生逻辑推理、数学运算等数学核心素养，考查数形结合思想、转化与化归思想、分类讨论思想、方程思想等数学思想方法.

3.几点思考

首先考虑教材内容、考纲要求以及近几年高考的命题风格和考查思路.近几年全国卷文科数学圆锥曲线解答题多数考查直线与圆的位置关系和直线与抛物线的位置关系，第一问通常求曲线方程.求动点的轨迹方程没有指定曲线作定向的提示，问题的开放性较大，更能考查学生的能力，但求指定曲线方程还可以兼顾对所指定曲线的性质和特征的考查，两种考法各有千秋.第二问主要是结合一条动直线与指定曲线的位置关系，根据试题素材提出有意义的问题.试题的解答过程力求更好地展现学生的思维过程，展现学生的推理论证能力、运算求解能力、分析问题与解决问题的能力，展现学生对数形结合思想、转化与化归思想、分类讨论思想、方程思想等数学思想方法的理解与掌握情况，展现学生数学运算和逻辑推理等数学核心素养的水平.

其次考虑学生的特点.文科生的数学能力总体水平没有理科生高，在试题难度和运算量的要求相对理科试题有所降低，因此问题“宽度”不宜太宽，问题指向要尽量明确.

最后考虑试题的区分度.控制试题解答长度，如果试题的解答长度太长或太短都会影响试题的区分度.试题入口要宽，问题由浅入深层层递进，有利于学生的解答和提高试题的区分度，这与全国卷的命题风格和命题思路基本吻合.

4.试题的命制

结合抛物线定义，求动点的轨迹方程作为试题的第一问，已知一条动直线与抛物线相交，坐标原点与两个交点连线的斜率之积为一个常数，两交点与坐标原点所围成的三角形面积为一个定值，要求学生根据题意列出两个方程并解方程，最后求出直线的方程.本道题的解答用代数方法解决几何问题，考查抛物线的定义和标准方程、韦达定理、直线方程、点到直线的距离公式等解析几何核心内容.能很好地考查学生的推理论证能力、运算求解能力、分析问题与解决问题的能力，考查学生逻辑推理和数学运算核心素养，考查数形结合思想、转化与化归思想、分类讨论思想、方程思想等数学思想方法，符合文科学生的特点.

二、试题与解答

题目：在平面直角坐标系xOy中，已知动圆M经过定点F(0,1)且与直线y+1=0相切，记动圆M的圆心M的轨迹为曲线C.

(1)求曲线C的方程；

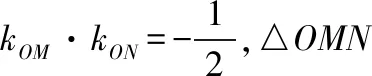
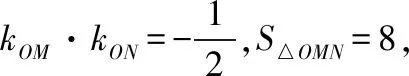
解：(1)设点M(x,y)，点M到直线y+1=0的距离为d，

依题意得|MF|=d，

根据抛物线定义可知，曲线C是以F(0,1)为焦点，直线y+1=0为准线的抛物线，

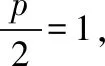
所以曲线C的方程为x2=4y.

(2)直线l的斜率显然存在.

设直线l:y=kx+b，M(x1，y1)，N(x2，y2),

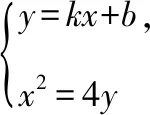
因为Δ=16k2+8b>0，

所以x1+x2=4k,x1x2=-4b，

因为y1y2=(kx1+b)(kx2+b)=k2x1x2+kb(x1+x2)+b2=b2，

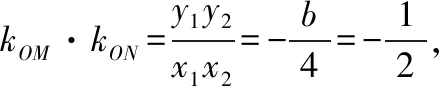
所以b=2，

故直线l方程为y=kx+2，

所以直线l恒过定点R(0,2)，

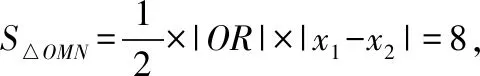
所以|x1-x2|=8，

即(x1+x2)2-4x1x2=64，

所以k2+b=4，

所以k2=2，

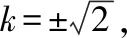
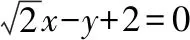
三、测评结果分析

经过测评获取的数据表明，难度系数与预估难度系数(估计难度系数0.45左右)基本一致.大部分学生第一问能得满分，与最初问题设置入口尽量要宽的要求高度吻合.相当多的学生能根据题意设直线方程、联立直线方程与抛物线方程，设交点坐标、用韦达定理，但是根据题意列出其中一个方程，能列出两个方程的人数就大大减少，由于运算求解能力等因素，能准确求出方程的解，并求出直线方程的人数就更加的少，最终本道试题能拿满分的学生并不是很多，这与命题时问题设置要求入口要宽，问题由浅入深层层递进，有利于学生的解答和提高试题的区分度息息相关，测评数据在合理的预设范围内，试题具有很好的区分度和信度与效度，是一道不错的试题.

四、原创试题促进教师专业发展