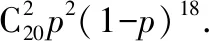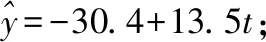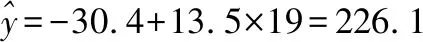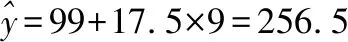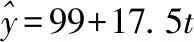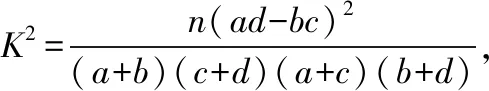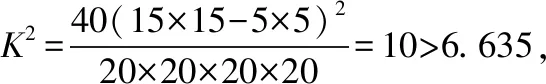高中数学核心素养研究之数学建模

湖北 项 欣 王卫华

数学核心素养是数学课程的基本理念和总体目标的体现，可以有效地指导数学教学实践.《普通高中数学课程标准(实验)》修订稿提出了数学学科的六种核心素养，即数学抽象、直观想象、数学建模、逻辑推理、数学运算和数据分析.提升数学建模核心素养，要求数学教师在课堂教学中强化学生的建模意识，教师在教学中通过设置数学建模活动，培养学生的建模能力.

一.数学建模核心素养的定义及相关价值

从数学建模的内涵看，数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养.数学建模过程主要包括：在实际情境中从数学的视角发现问题、提出问题、分析问题、建立模型、确定参数、计算求解、检验结果、改进模型，最终解决实际问题.

从数学建模的学科价值看，数学建模素养是学生在数学建模活动中形成的，它集理解问题、提出问题、分析问题和解决问题于一身，是最具有综合性的数学素养.数学模型素养搭建了数学与外部世界的桥梁，是数学应用的重要形式.数学建模是应用数学解决实际问题的基本手段，也是推动数学发展的动力.

从数学建模的教育价值看，通过高中数学课程的学习，学生能有意识地用数学语言表达现实世界，发现和提出问题，感悟数学与现实之间的关联,学会用数学模型解决实际问题，积累数学实践的经验,认识数学模型在科学、社会、工程技术诸多领域的作用，提升实践能力，增强创新意识和科学精神.

二.数学建模核心素养的学业质量水平划分

每一个数学学科核心素养划分为三个水平，每一个水平是通过数学学科核心素养的具体表现和体现数学学科核心素养的情境与问题，知识与技能，思维与表达，交流与反思四个方面进行表述.数学建模的三个水平表述如表：

水平一是高中毕业应当达到的要求，也是高中毕业的数学学业水平考试的命题依据；水平二是高考的要求，也是数学高考的命题依据；水平三是基于必修、选择性必修和选修课程的某些内容对数学学科核心素养的达成提出的要求，可以作为大学自主招生的参考.

三、数学建模的特点

数学模型是由数字、字母或其他数学符号组成的，描述现实对象数量规律的数学公式、图形或算法.也就是说，数学模型就是通过抽象和简化，把某一特定的问题或者具体事物的某种具体特征和内在联系使用数学语言、数学方法表达出来并将问题解决.作为反映实际问题的数学模型，具有逼真性和可行性，抽象性和转移性，多样性和优化性.

1.逼真性和可行性

通常情况下，作为解决现实问题的数学模型，要求越是逼真越好，但越逼真的数学模型，在数学处理上越复杂，需要考虑的因素就越多，甚至需要跨多学科建模，不易达到解决问题的目的.在高中数学建模时，可以适时简化考查因素，设置建模预期目标，只要能达到预期目标就是可行的.比如在解决贷款买房的问题时，我们在高中阶段要忽略通货膨胀的因素等.

2.抽象性和转移性

数学模型就是通过抽象和简化，把某一特定的问题或者具体事物的某种具体特征和内在联系使用数学语言、数学方法表达出来并将问题给予解决.对于某一特定问题建立的数学模型可以转移到其他适当的领域使用.比如解决了贷款买房的问题，我们也可以用相同的模型解决退耕还林的问题.

3.多样性和优化性

数学建模建立的数学模型，随着时间的变化，以前建立的模型的诸多因素将发生变化，不可能总用现成的数学模型去解决问题，要认识到数学建模的多样性，对同一问题的数学模型需要不断优化.

四.数学建模素养的具体体现及案例

数学建模是将实际问题中的因素进行简化，抽象变成数学中的参数和变量，运用数学理论进行求解和验证，并确定最终是否能够用于解决问题的多次循环.数学建模能力包括转化能力、数学知识应用能力、创造能力和沟通与合作能力.数学建模主要表现为：发现和提出问题、建立和求解模型、检验和完善模型、分析和解决问题.

高中数学建模的主要知识载体：平面向量及应用、复数、概率、数列、一元函数导数及应用、空间向量与立体几何、平面解析几何、计数原理.

从现行的高中数学教材，笔者找到了以下几个例子，可以从现实生活中的实际问题切入，培养数学建模的思想，并开展活动.

1.函数最值的研究

可以由现实生活中的面积、体积的最值、用料最省、费用最低等问题引入，发现和提出问题，引导出函数模型，提出函数单调性的概念及性质等知识，最终帮助解决最值问题.在教学中，还可以穿插强调函数图象的教学，增强数形结合的意识，最后提出投资方案的选择问题(必修一3.2函数模型及其应用)，建立一次函数、二次函数、指数函数等模型，直观用函数知识解决实际问题，做到能多次循环解决同类型的问题.

2.三角函数的应用(解三角形)

可以由现实生活中的测量问题、足球射门角度问题、观察的最大视角问题、缉私船的追击方向问题等，引入对三角函数的应用，建立相关解三角形数学模型(什么情况下用正弦定理，什么情况下用余弦定理).

3.数列的实际应用

可以由现实生活中的房贷分期还款、存款利息、利润增长等问题引入用数列的相关知识建立数学模型.

4.概率统计的应用

5.立体几何的应用

可以由现实生活中的体积、面积、长度测量与极值问题、几何体的最佳设计等问题引入用立体几何的相关知识建立数学模型.

6.解析几何的应用

可以由现实生活中的拱桥及卫星轨道的设计问题、投掷项目的最远距离问题、简单的线性规划问题等引入用解析几何的相关知识建立数学模型.

五.2018年高考试题中数学建模素养的案例分析

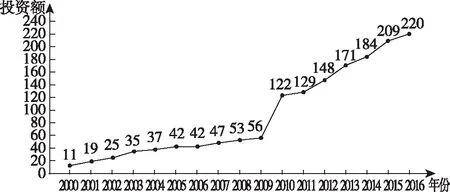
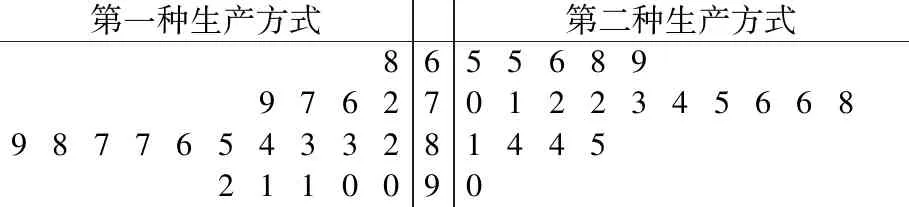
例1.(2018全国卷Ⅰ理·20题)某工厂的某种产品成箱包装，每箱200件，每一箱产品在交付用户之前要对产品作检验，如检验出不合格品，则更换为合格品.检验时，先从这箱产品中任取20件作检验，再根据检验结果决定是否对余下的所有产品作检验，设每件产品为不合格品的概率都为p(0

(Ⅰ)记20件产品中恰有2件不合格品的概率为f(p)，求f(p)的最大值点p0；

(Ⅱ)现对一箱产品检验了20件，结果恰有2件不合格品，以(Ⅰ)中确定的p0作为p的值.已知每件产品的检验费用为2元，若有不合格品进入用户手中，则工厂要对每件不合格品支付25元的赔偿费用.

(ⅰ)若不对该箱余下的产品作检验，这一箱产品的检验费用与赔偿费用的和记为X，求EX；

(ⅱ)以检验费用与赔偿费用和的期望值为决策依据，是否该对这箱余下的所有产品作检验？

(Ⅱ)由(Ⅰ)知，p=0.1.

本次会议还对优秀品牌、优秀产品进行了表彰。品牌类：美菱荣获2018年中国电冰箱行业保鲜领导品牌；美的荣获2018年中国电冰箱行业智能领军品牌；海尔荣获2018年中国电冰箱行业科技领袖品牌；TCL荣获2018年中国电冰箱行业智慧健康创新品牌。产品类：奥马纤薄系列冰箱荣获2018年中国电冰箱行业完美嵌入时尚先锋。

(ⅰ)令Y表示余下的180件产品中的不合格品件数，依题意知，Y～B(180,0.1),X=20×2+25Y,即X=40+25Y,所以EX=E(40+25Y)=40+25EY=490.

(ⅱ)如果对余下的产品作检验，则这一箱产品所需要的检验费为400元.由于EX>400，故应该对余下的产品作检验.

案例评析：本题以产品检测质量的现实应用问题为切入口，考查了独立事件、二项分布等概念，同时考查了利用导数知识求解最值的跨章节知识点.通过对随机变量期望考查学生的数据处理能力，更考查实际问题化归为数学问题的数学建模思想.

例2.(2018全国卷Ⅱ理·18题)如图是某地区2000年至2016年环境基础设施投资额y(单位：亿元)的折线图.

(Ⅰ)分别利用这两个模型，求该地区2018年的环境基础设施投资额的预测值；

(Ⅱ)你认为用哪个模型得到的预测值更可靠？并说明理由.

解：(Ⅰ)利用模型①，该地区2018年的环境基础设施投资额的预测值为

利用模型②，该地区2018年的环境基础设施投资额的预测值为

(Ⅱ)利用模型②得到的预测值更可靠.

(ⅱ)从计算结果看，相对于2016年的环境基础设施投资额220亿元，由模型①得到的预测值226.1亿元的增幅明显偏低，而利用模型②得到的预测值的增幅比较合理.说明利用模型②得到的预测值更可靠.

案例评析：数学建模本质上就是一个解决问题的过程.本题以实际问题环境基础设施投资额为切入口，考查学生选取适当的数据，利用函数拟合的方法进行预测，并根据实际背景对结果进行预测的解决问题的能力.建立函数模型解决实际问题的数学建模素养得以充分呈现.

例3.(2018全国卷Ⅲ理·18题)某工厂为提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率，选取40名工人，将他们随机分成两组，每组20人，第一组工人用第一种生产方式，第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位：min)绘制了如下茎叶图：

第一种生产方式第二种生产方式86556899762701223456689877654332814452110090

(Ⅰ)根据茎叶图判断哪种生产方式的效率更高？并说明理由；

(Ⅱ)求40名工人完成生产任务所需时间的中位数m，并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表；

超过m不超过m第一种生产方式第二种生产方式

(Ⅲ)根据(Ⅱ)中的列联表，能否有99%的把握认为两种生产方式的效率有差异？

P(K2≥k)0.0500.0100.001k3.8416.63510.828

(Ⅰ)第二种生产方式的效率更高.

理由如下：(ⅰ)由茎叶图可知：用第一种生产方式的工人中，有75%的工人完成生产任务所需时间至少80分钟，用第二种生产方式的工人中，有75%的工人完成生产任务所需时间至多79分钟.因此第二种生产方式的效率更高.

(ⅱ)由茎叶图可知：用第一种生产方式的工人完成生产任务所需时间的中位数为85.5分钟，用第二种生产方式的工人完成生产任务所需时间的中位数为73.5分钟.因此第二种生产方式的效率更高.

(ⅲ)由茎叶图可知：用第一种生产方式的工人完成生产任务平均所需时间高于80分钟；用第二种生产方式的工人完成生产任务平均所需时间低于80分钟，因此第二种生产方式的效率更高.

(ⅳ)由茎叶图可知：用第一种生产方式的工人完成生产任务所需时间分布在茎8上的最多，关于茎8大致呈对称分布；用第二种生产方式的工人完成生产任务所需时间分布在茎7上的最多，关于茎7大致呈对称分布，又用两种生产方式的工人完成生产任务所需时间分布的区间相同，故可以认为用第二种生产方式完成生产任务所需的时间比用第一种生产方式完成生产任务所需的时间更少，因此第二种生产方式的效率更高.

以上给出了4种理由，考生答出其中任意一种或其他合理理由均可得分.

列联表如下：

超过m不超过m第一种生产方式155第二种生产方式515