一种新的武器装备体系能力指标变权算法

管清波, 冯书兴

(1.装备学院航天指挥系,北京101416; 2.装备学院训练部,北京101416)

一种新的武器装备体系能力指标变权算法

管清波1, 冯书兴2

(1.装备学院航天指挥系,北京101416; 2.装备学院训练部,北京101416)

考虑奇异指标值对指标权重的影响,设计了一种变权算法,分别对存在正偏和负偏奇异指标值的指标权重进行了修正,使综合评价结果更具科学性和客观性;与现有的变权算法相比,不仅考虑了过劣指标值对权重的影响,还考虑了过优指标值对权重的影响;最后通过实例分析证明了该方法的有效性。

指标权重;变权算法;奇异指标值;正偏;负偏

武器装备体系能力常常通过多个指标来度量,在对多项指标进行综合时,由于各指标在综合效能评价中的作用和地位不同,常需要通过给各指标赋予权值来描述这一差异,这就是指标权重。指标权重是对指标相对重要性程度的主观评价和客观反映的综合度量,是影响评价结果的重要因素之一,权重分配的合理性将直接关系到评估结果的科学性[1-2]。目前,确定权重的方法通常分为主观赋权法和客观赋权法,如采用专家经验法、层次分析法、主成分分析法等,这些方法主要考虑指标间的相对重要程度,而不考虑指标的实际能力(指标值)。随着信息化程度的不断提高,武器系统越来越复杂,系统内部各要素、系统之间的相互关系也越来越复杂,只有当各项指标能力相对均衡时,武器装备体系的综合效能才会得到很好的发挥。从指标权重的角度来讲,就是各评价指标对系统效能的影响程度不仅与其相对重要性有关,还会随着该项指标值的劣化或优化而发生变化,即,当指标体系中存在个别很大或很小的指标值时,指标权重不仅与相对重要性有关,还与指标值有关,即各项指标的权重随着其指标值的大小而变化。为了解决这种问题,文献[3-5]提出了基于熵的评估权重修正方法,在先验评估权重的基础上,依据每位评价人员的评分情况,对评估权重进行熵修正,其变权处理的目的是弱化评分人员的不客观和不科学性;文献[6-8]提出的模糊变权法,主要对能力偏小甚至不存在的指标权重进行了处理,但未考虑偏大指标值的情况;文献[9]虽然未对指标权重进行处理,但通过惩罚函数对指标值进行了修正,间接起到了调整权重的作用,该方法未对惩罚函数中的阈值给出确定准则。本文提出的变权处理算法,不仅考虑了过劣指标值对权重的影响,还考虑了过优指标值对权重的影响,能满足决策人的“均衡”原则,使综合评价结果更具科学性和客观性。

1 变权算法基本思想

变权思想认为,评估的目的是进行方案的选择,方案的选用与否除了取决于综合评价的优劣,还要考虑综合评价结果由于受个别指标的影响而出现偏大或偏小的情况。因此,当指标值中存在个别过小或过大的指标值时,指标权重就不仅只反映指标的相对重要性,而同时也要反映个别指标值的影响。变权算法的基本思想如下。

1)当评价指标中的个别指标值远小于其他指标值时,就说明该项指标值过小,可能会严重影响系统的整体效能,甚至会对系统效能起决定性作用,这就需要对基本权重进行调整,适当地突出评估指标值较低的因素,即适当加大该指标权重,以引起决策者重视。

2)当评价指标中的个别指标值远大于其他指标值时,说明该项指标值过大,可能会引起综合评价结果因单一指标的贡献度过大而较高。实际上,对于复杂的现代武器装备体系而言,由于各类能力相互支撑、相互制约,单要素功能的发挥要依靠其他要素乃至整个体系的支撑,若其他指标值相对均衡,单一过优指标值对整体效能的贡献就十分有限,因此也需要对基本权重进行调整,适当弱化评估指标值过高的因素,即适当减小该指标权重,以防止决策者盲目乐观。

2 变权算法基本过程

设对某武器装备体系的不同备选方案进行能力评估,共有N个评估指标,分别为A1,A2,…, AN,对每一项评估指标进行单项评估,可获得指标值u1,u2,…,uN,根据指标特性按照一定的规范化算法进行处理,处理后的指标值e1,e2,…,eN为[0,1]之间的数。通过常规方法比较指标相对重要性,获得的指标权重为基础权重w=(w1, w2,…,wN)。武器装备体系能力综合评价一般通过线性加权求和的方式获得,即ei。根据变权算法修正后的权重w′是基础权重和指标值的函数,即w′i=f(wi,ei)。f(wi,ei)为变权函数。变权算法的基本过程如图1所示。

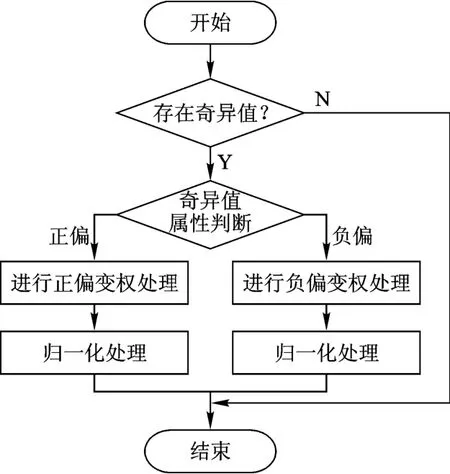
图1 变权算法过程

3 变权算法描述

3.1 奇异指标值存在及属性判断

变权函数主要是对指标值过小或过大的指标权重进行处理,在进行变权处理之前,首先应该明确什么样的指标值是过小或过大的。由于指标值是经过规范化后的[0,1]中的无量纲数据,指标值实际上是对该项指标的性能度量,当各项指标值比较接近时,可认为系统各项能力比较匹配,按常规方法确定的指标权重不需要作调整;而当个别指标值远小于或远大于其他指标值时,通过加权和综合得出的能力值无法真实反映系统能力,从而需要对基本权重进行调整。这时,需要确定阈值,以判断指标值是否过小或过大。

在统计学中,奇异值是指一组数据中明显不同于其他数据的数据项,在一组指标值中,奇异值即为过小或过大的指标值[10]。一组评价指标中是否存在奇异值,可采用以下过程来判断。

1)计算集中趋势度,用于估计这组指标值的中心值。集中趋势度常采用算术平均数e和中位数来描述。

2)计算指标值离散度,用于判断这组数据的分散程度。标准差σ描述了这组指标值的离散程度。标准差越小,说明越多的数据分散在平均数的周围。

3)判断是否存在奇异值。统计在±1个标准差范围内指标值的个数i。

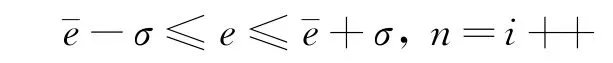
如果n/N＞0.8,则意味着80%的指标值落在平均数周围±1个标准差范围内,20%在其外,由此可判定指标值存在过大或过小的奇异值。

4)判断奇异值的属性。由于算术平均值容易受奇异值的影响,而中位数不受奇异值的影响,对于非正态分布的数据组,二者之间存在差异,由此可作为判断奇异值的属性,即指标值是过大还是过小。

3.2 调节函数及变权处理

2)定义调节函数。对于具有过小指标值的指标,需增加该项指标的权重,正偏变权处理的调节函数为

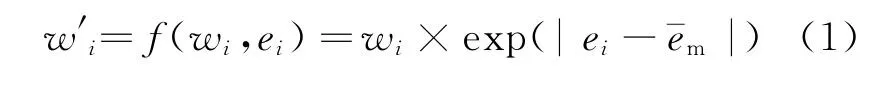
对于具有过大指标值的指标,需降低该项指标的权重,负偏变权处理的调节函数为

3)对调节后的各指标权重进行归一化处理,获得变权后的指标权重为

4 实例分析

4.1 基本数据描述

为了说明算法的可用性和有效性,以某武器装备体系能力评价为例进行分析。该装备体系能力评价指标分别为态势感知能力、指挥决策能力、精确打击能力、快速机动能力、全维防护能力和综合保障能力,假设各项评价指标同等重要,即评价指标的基础权重w为等权,即

假设有2组评价指标值,分别对组一、组二的指标进行评价并进行无量纲化处理,处理后的评价指标值分别为e1,e2：

e1=(0.98,0.99,0.85,0.87,0.69,0.16)

e2=(0.98,0.12,0.13,0.25,0.23,0.22)

4.2 变权处理

对于组一的评价指标值,计算可得：

±1个标准差范围为[0,0.648 7],有5个指标值在该区间内,比例为83.3%,存在奇异值。因,正偏,存在小的奇异值。根据式(1),可得变权处理结果,见表1。

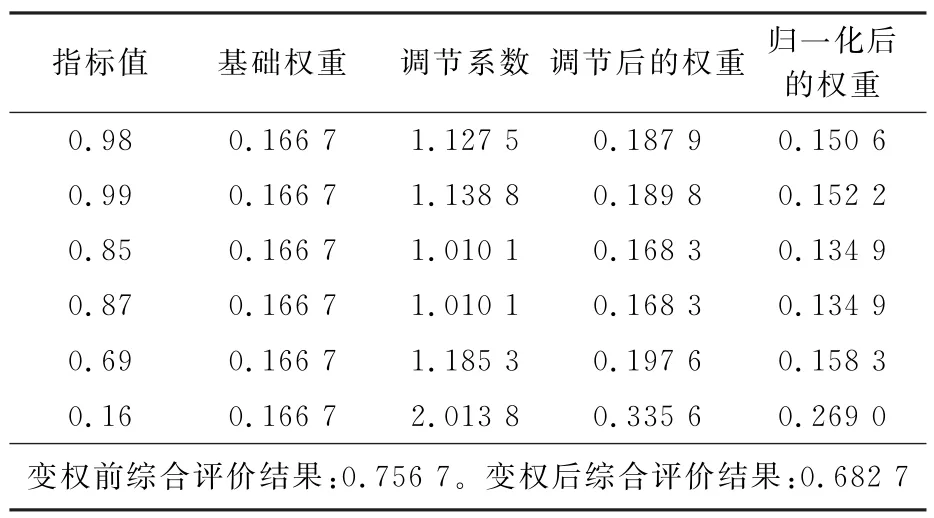
表1 个别指标值过小情况的变权处理结果

对于组二的评价指标值,计算可得：

±1个标准差范围为[0.444 8,1],有5个指标值在该区间内,比例为83.3%,存在奇异值。因,负偏,存在大的奇异值。根据式(2),可得变权处理结果,见表2。

表2 个别指标值过大情况的变权处理结果

4.3 结果对比分析

经变权处理后,权重变化对比见图2～图3。

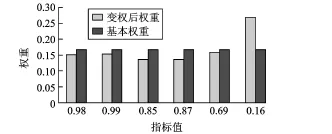
图2 组一指标变权前后的指标权重对比

图3 组二指标变权前后的指标权重对比

由图2可以看出,指标值0.16与其他指标值相比过小,为奇异值,经变权处理后指标权重变化相对较大,由原来的0.166 7增加为0.269 0,相对重要性有所增加。图4的综合评价结果(组一)也表明,变权后总体评价结果减小,突出了较小指标值的影响。

由图3可看出,指标值0.98于其他指标相比过大,为奇异值,经变权处理后指标权重变化相对较大,由原来的0.166 7减少为0.123 1,相对重要性有所降低。图4的综合评价结果(组二)也表明,变权后总体评价结果减小,弱化了较大指标值的影响。

图4 变权前后的综合评价结果对比

5 结束语

本文提出的变权算法,不仅考虑了诸因素的相对重要性,而且考虑了各指标权重随指标值优劣的不同而变化情况,突出或弱化了奇异指标值的影响。通过变权处理算法可以更客观地反映武器装备体系各项能力指标间关系的复杂性和贡献度,可为决策者提供客观、科学的决策支持。

References)

[1]杨建国,龙光正,赵保军.武器装备发展论证[M].北京：国防工业出版社,2009：55-57.

[2]杜栋,庞庆华,吴炎.现代综合评价方法与案例精选[M].北京：清华大学出版社,2008：14-18.

[3]邱菀华.管理决策熵学及其应用[M].北京：中国电力出版社,2011：156-166.

[4]朱令娴,汤明端,邓本江.基于相对重要性和熵修正的评估权重设置方法[J].计算机工程与设计,2012,33(9)：3451-3453.

[5]ZHANG Limin,WANG Qinbo,ZHONG Luo.Optimized evaluation of variable weight on performance of computer engineering project investment[C]//IEEE.2012 2ndInternational Conference on Consumer Electronics,Communications and Networks(CECNet).Wuhan,China：Wuhan University,2012：1445-1449.

[6]彭祖赠,孙韫玉.模糊数学(Fuzzy)及其应用[M].武汉：武汉大学出版社,2002：118-167.

[7]朱勇珍,李洪兴.状态变权的公理化体系和均衡函数的构造[J].系统工程理论与实践,1999(7)：116-120.

[8]杨建宏,韩林.模糊变权法在通信指挥效能评估上的应用[J].空军工程大学学报：自然科学版,2003(4)：41-44.

[9]孟庆均,宋爱斌,金万峰.基于惩罚函数的C4ISR系统效能指标聚合方法[J].装甲兵工程学院学报,2008,22(3)：5-8.

[10]EVANS J R,OLSON D L.数据、模型与决策[M].2版.杜本峰,译.北京：中国人民大学出版社,2006：45-87.

(编辑：王高翔)

A Novel Variable Weight Algorithm for Equipment System Capability

GUAN Qingbo1, FENG Shuxing2

(1.Department of Space Command,Equipment Academy,Beijing 101416,China; 2.Training Department,Equipment Academy,Beijing 101416,China)

Considering the influence of singular index value,a novel variable weight algorithm is designed.Employing this algorithm,some index value which have positive bias or negative bias will be amended,which will lead synthesize assessment to more reasonable and more objective.Compared with existing variable weight algorithm,this algorithm considers influence of both inferior index value and superior index value.Finally,an example is shown to prove its validity.

index weight value;variable weight algorithm;singular index value;positive bias; positive bias

TP 311;E 917

2095-3828(2014)01-0112-04

ADOI10.3783/j.issn.2095-3828.2014.01.025

2013-06-13

管清波(1967-),女,教授,硕士生导师.主要研究方向：航天信息支援.