基于主成分分析方法的作战单元的作战能力生成研究

吴 坚, 郭齐胜, 穆 歌, 周扬童, 白 桦

(1.装甲兵工程学院装备指挥与管理系,北京100072; 2.沈阳军区司令部,辽宁沈阳110011)

基于主成分分析方法的作战单元的作战能力生成研究

吴 坚1, 郭齐胜1, 穆 歌1, 周扬童2, 白 桦1

(1.装甲兵工程学院装备指挥与管理系,北京100072; 2.沈阳军区司令部,辽宁沈阳110011)

为解决难以应用作战单元的作战任务定量生成其作战能力的问题,引入主成分分析方法(principal components analysis,PCA),对作战单元的作战任务度量指标进行集成,分析其中的要素关系,提取作战效能影响成分,生成作战能力。解决了利用作战单元的作战任务度量指标开发作战能力的问题,为作战能力的生成提供了一种定量分析的方法。

主成分分析方法;作战单元;作战能力;方法研究

作战能力通常用来反映作战指挥机构、装备需求开发部门对部队和装备战斗力的期望,也能用来体现工业部门研制装备的技术水平。作战能力可以用部队及其装备战斗效能优劣的综合性、整体性的指标来衡量。作战单元的作战能力生成将有利于评估和比较各军兵种部队及其装备的作战效能,科学分析敌我双方的战斗力及其影响作战胜负的相关因素,可以辅助指挥员科学预测作战结果,合理编成作战力量,客观优选作战方案,以取得最优的作战效果;也可帮助装备需求开发人员准确理解军事人员的作战需求,并将装备需求有效地传递给装备设计人员,对于武器装备的发展规划、设计论证、研制生产和作战使用都有着现实意义。

1 作战能力的概念及生成机理阐述

作战能力[1]是指不同的作战层次的作战力量,对相应层次的作战目标(使命)的实现能力,它可具体分解为多项作战能力目标。作战能力目标是指在不同的作战层次(战略、战役或战术),为实现作战目标或支持作战活动的定量或定性的陈述。作战能力的形成过程[2]包括：根据作战任务的流程,确定关键的作战节点概念和它们之间的联系;分析影响关键节点之间因果关系的外在因素;分析每个关键节点和影响因素的属性,建立评估度量指标集;研究关键节点间的能力传递函数。结合上述相关概念描述,作战能力生成可以看作基于作战效果的,面向不同作战层次作战单元提出的,在完成其设定的使命任务前提下,作战单元所需的作战能力(结构化的能力支持描述)的开发流程(使命任务与作战单元的关系、使命任务的效能需求分析、作战单元的作战能力描述)及其量化分析技术研究。

作战能力的生成机理多样且复杂,总体可以归纳为以下几种：一是从新的作战使命直接提出的作战能力,这种生成机理开发的作战能力描述通常是一种顶层的作战能力概念设想,比较抽象,需要进一步解释和进行规范化描述。二是由新技术衍生的可直接支持作战的作战能力,这种生成机理开发的作战能力描述通常是一种功能描述,比较具体,但它与现有作战能力体系的作用关系(例如：在作战能力体系中的层次位置,与其他作战能力结合可能涌现的新作战能力,等等)需要深入研究。三是从作战任务分析得到的作战能力,这种生成机理规避了前2种机理的缺陷,开发的作战能力描述往往具体准确、组成关系清晰,是当前较为常用的作战能力开发机理。它主要采用“威胁—使命域—任务清单—能力清单—功能域”的机理开发结构,利用作战单元作为作战任务和作战能力的生成媒介,通过分析其中的关联开发作战能力,如图1所示。

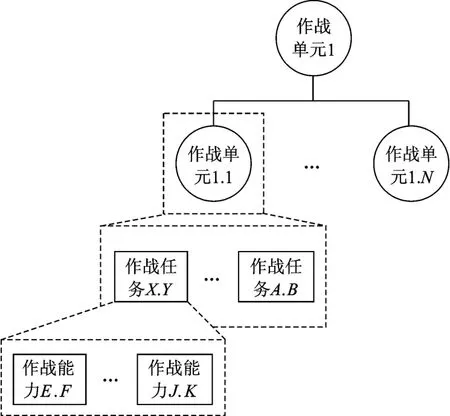
图1 作战单元、作战任务和作战能力的关系图

作战单元是依据研究粒度确定的一定规模的部(分)队,是实施作战任务的主体,包括人员和装备,客观上应具有完成作战任务的作战能力。作战任务是武装力量在作战中所要达到的目标及承担的责任。图1可以反映出3个内容要素：①每个作战单元要完成相应的作战任务,并应具有相应的作战能力;② 作战单元与作战任务、作战能力的层次结构并不一定一一对应;③ 完成作战任务需要有相应的作战能力支持。

因此,根据作战单元、作战任务和作战能力的关系可以获得一种作战能力生成的研究思路,即分析一个作战单元需要完成的作战任务,将每个作战任务分解为若干度量指标,并将度量指标的效能分析集成,以此生成相应的作战能力。但由此引发的问题是：作战任务的度量指标众多,指标间的关系复杂,指标集成反映出的作战效能往往是线性相关的,难以仅凭定性分析获得合理准确的作战能力。所以,如何分析作战任务度量指标的综合效能,并以此揭示实施作战任务所需要的作战能力,是亟待解决的一个难题。

2 主成分分析法简介

主成分分析法[3](PCA)也称主分量分析或矩阵数据分析方法,是一种简化数据集的技术,可以将系统中的多个变量(或指标)转化为较少的几个综合变量(或综合指标),因此,可将多变量的高维空间问题简化为低维的综合指标问题,能反映系统信息量最大的综合指标为第1主成分,其次为第2主成分。其原理在于：通过发现原有样本变量x间的关系,简化变量x,并根据指标的得分值在指标轴空间对x进行分类处理,以便将众多线性相关的指标转化为少数线性无关的指标,便于运用这些指标对研究的系统进行准确的分析研究。这些指标的个数,通常按需要反映的全部信息的百分比来确定,指标之间是互不相关的。

由此可见,主成分分析主要具有以下功能。

1)主成分分析能降低所研究的数据空间的维数。即用研究M维的Y空间代替P维的X空间(M＜P),而低维的Y空间代替高维的X空间所损失的信息很少,是一种删除冗余变量的方法。

2)通过因子负荷αij的结论,可分析X空间变量间的某些关系。

3)用主成分分析筛选回归变量,有着重要的实际意义：便于从原始变量所构成的子集合中选择最佳变量,构成最佳变量集合,从而使模型本身易于结构分析、控制和预测。

所以,用主成分分析筛选变量,可以用较少的计算量来选择变量,进而获得选择最佳变量子集合。可以应用这些功能原理解决作战能力生成问题,开发基于主成分分析方法的作战能力生成方法。

3 基于主成分分析方法的作战能力生成步骤

Step 1对某作战单元的作战任务的原始指标数据进行标准化,即采集其p维随机向量x= (x1,x2,…,xp)T的n个样本xk=(xk1,xk2,…, xkp)T,k=1,2,…,n,n＞p,构造样本阵,对样本阵元进行如下标准化变换[4]

式中：x0ik为作战任务的指标样本原始参数;

由此获得标准化的作战任务指标样本矩阵x,即

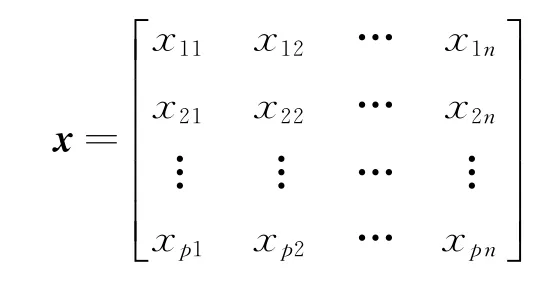
Step 2定义指标样本矩阵x的相关矩阵为R[5],则应用

式中：xT是x的转置矩阵;i,j=1,2,…,p。

求得作战任务的指标样本的相关矩阵R,R的对角元素rij(i=1,2,…,p)均为1,且p。

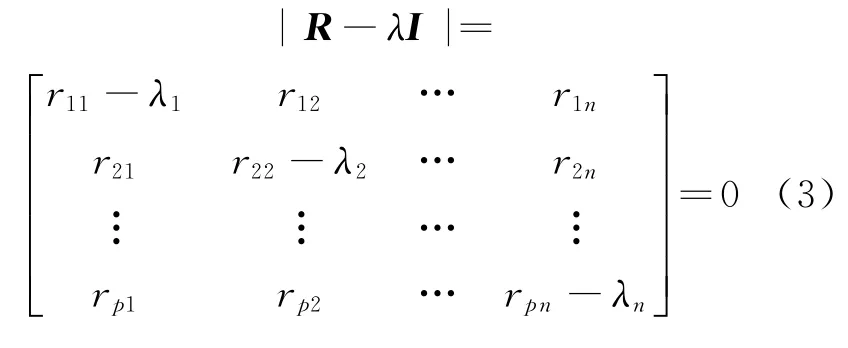
Step 3根据相关矩阵R的特征原理[6],可知：|R-λI|=0。即可应用求得相关矩阵R的特征根λ,其中λ1＞λ2＞…＞λp≥0,λ1+λ2+…+λp=p;相关矩阵R的特征向量为一个正交矩阵L[7],即

式中对应于λ1的特征向量为L1=(l11,l12,…, l1p),其余依次类推。

Step 4将相关矩阵R的特征根λ代入

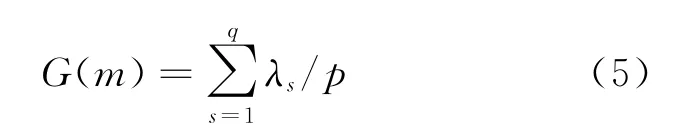
计算q个主成分的累积贡献率G(m)[8],并根据作战能力开发要求的G(m)确定主成分个数。根据作战能力的开发经验,通常取q个主成分,要求(λ1+λ2+…+λp)/p∈[0.6,0.8],即总方差的误差在(0.2,0.4)之间就能满足要求,所以,如果就可以确定所需的主成分个数。

Step 5计算相关矩阵R的特征向量L获取特征向量表,进而得到主成分yp的线性表达式[9],即

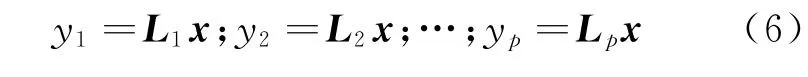
S

tep 6根据主成分yp的线性表达式,利用因子负荷量[10]25

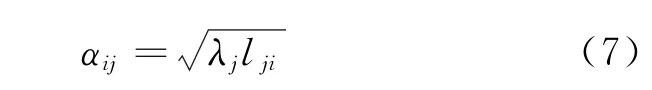
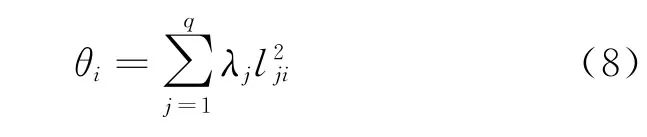
利用总贡献率[10]26分别统计分析各主分的因子负荷量和总贡献率,作为下一步的研究分析基础和依据。

Step 7根据以上计算结果,对影响作战任务完成的各主分作用进行分析,进而生成支持作战任务的作战能力。

4 算例分析

本文以某装甲部队“实施要地冲击”作战任务的作战能力生成为例。实施要地冲击是步兵或伞兵、坦克等快速冲向敌重要地区或目标的战斗行动,该作战任务具有“冲击距离、冲击速度、生存率和重型装甲比例”4项度量指标,见表1。

对某装甲部队9种典型作战样式中,达成作战任务的理想度量指标进行采集(通过仿真、兵推、实验或训练等方式),以此作为该作战任务的原始指标数据。

首先利用式(1)对数据进行标准化变换,再利用式(2)得到该作战任务指标样本的相关矩阵R,见表2。

表1 “实施要地冲击”度量指标

表2 标准化处理结果

通过式(3),求得相关矩阵R的特征根：λ1= 2.17,λ2=0.87,λ3=0.57,λ4=0.39,根据式(5)计算累积贡献率,根据研究要求,设主成分的累积贡献率G(m)≥75%,则可确定有效主成分个数。因为所以只需设定2个主成分就可以反映“实施要地冲击”的能力。利用式(4)计算特征向量,则对应于λ1和λ2的特征向量分别为L1=(l11,l12,l13,l14),L2=(l21, l22,l23,l24)分析λ1和λ2的特征向量,获得特征向量表,如表3所示。

表3 特征向量表

由特征向量表和式(6)可以得到主成分的线性方程式：

y1=0.46x1+0.48x2+0.52x3+0.54x4

y2=0.70x1+0.59x2-0.58x3-0.56x4

可以发现主成分y1和y2应该反映作战任务的2种能力水平,并采用式(7)和式(8)计算其因子负荷量和总贡献率,如表4所示。

表4 因子负荷量和总贡献率表

表4中,第1主成分y1对应的因子负荷量均为正数,表示冲击距离、冲击速度、生存率和重型装甲比例的水平提高都可以使y1提高,所以y 1反映了“实施要地冲击”的整体水平。其中x4的因子负荷量最大,反映重型装甲的比例在评价部(分)队实施冲击的效果时占有非常重要的作用。在经过术语分析可以选择用“装甲突击能力”来表示。

第2主成分y2的因子负荷正负都有,其中冲击距离、冲击速度为正,生存率、重型装甲比例为负,可以看出2组能力间的相互制约关系,冲击距离、冲击速度反映机动效能,生存率、重型装甲比例反映防护效能。在经过术语分析可以选择用“突击效能结构力”来表示。

由以上计算和分析可知(如图2所示)：某装甲部队需要实施的作战任务之一是“实施要地冲击”,支持该作战任务实施的作战能力是“装甲突击能力、突击效能结构力”。如果要获得该装甲部队的其他作战能力,还需对另外的作战任务进行集成分析。如果要对该装甲部队的作战能力做进一步分解,可以按照研究粒度将该装甲部队分解为下层作战单元,通过分析下层作战单元的作战任务度量指标生成相应的下层作战能力。最后,可以应用解释结构模型法(interpret structural model,ISM)技术,对所获得的作战能力的结构进行分析整合,生成“树状”层次结构的作战能力体系,并可应用关联矩阵建立作战任务体系与作战能力体系的关联关系。

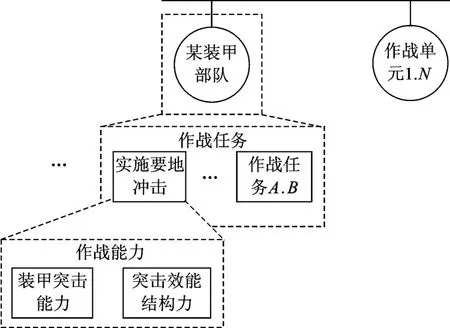
图2 某装甲部队及其作战任务、作战能力的关系图

5 结 论

本文初步提出了应用主成分分析法集成作战单元的作战任务度量指标、定量生成作战能力的方法。为下一步开发我军高度结构化的作战能力清单,提供了理论和方法指南。同时,将提高作战能力分析的质量,进而提升我军作战指挥和训练的战技水平,增强我军装备需求论证的效能和效益。但是,如何将该方法与前期的作战任务生成技术进行有机结合,在一些细节方面还需要进一步完善和深入研究。

References)

[1]段采宇,余博超,周敏龙,等.信息化战争条件下军事需求分析之作战能力需求研究[J].需求工程,2007(7)：14-17.

[2]邓克波,毛少杰.作战能力形成过程的建模方法初探[J].指挥信息系统与技术,2010(3)：6-9.

[3]吴翊.应用数理统计[M].长沙：国防科技大学出版社, 1995：32.

[4]汪应洛.系统工程方法理论与应用[M].北京：机械工业出版社,2003：146-150.

[5]高惠漩.应用多元统计分析[M].北京：北京大学出版社, 2005：16-18.

[6]徐雅静,汪远征.主成分分析应用方法的改进[J].数学的实践与认识,2006,36(6)：68-75.

[7]何晓群.多元统计分析[M].北京：中国人民大学出版社, 2004：14-17.

[8]傅荣林.主成分综合评价模型的探讨[J].系统工程理论与实践,2001,21(11)：68-74.

[9]姜春燕,林和平,刘丁慧,等.灰主成分分析研究及其应用[J].吉林大学学报：信息科学版,2007,25(5)：510-517.

[10]张尧庭,方开泰.多元统计分析引论[M]北京：科学出版

社,1999.

(编辑：王高翔)

Research on Method for Developing the Operational Capability of Operational Unit Based on Principal Components Analysis

WU Jian1, GUO Qisheng1, MU Ge1, ZHOU Yangtong2, BAI Hua1
(1.Department of Equipment Command and Administration,Academy of Armored Forces Engineering,Beijing 100072,China; 2.Headquarters of Shenyang Military Command,Shenyang Liaoning 110011,China)

To resolve the problems that are difficult to develop operational capability by using operational unit's operational task,the paper introduces the principal components analysis(PCA)technology to integrate the index of measurement of the operational task of operational unit,analyzes the relationship between its elements,extracts the influence factors of operational efficiency,and develops the operational capability.The problem that develops the operational capability by using the index of measurement of the operational task of operational unit is solved.It takes a method of developing the operational capability by quantitative analysis.

principal components analysis(PCA);operational unit;operational capability; methods research

E 917

2095-3828(2014)01-0120-05

ADOI10.3783/j.issn.2095-3828.2014.01.027

2013-03-05

吴 坚(1978-),男,讲师,博士.主要研究方向：武器装备需求论证.1412301717@qq.com.