含空腔点阵增强夹芯结构的固有振动分析方法

王祖华，殷洪

武汉第二船舶设计研究所，湖北武汉430205

0 引 言

含空腔点阵增强夹芯结构由面板和内含多种组分的复杂芯层组成，是一种兼具力学和声学性能的夹层吸声复合材料。沿厚度方向植入的增强柱能够较好地提高夹芯结构的承载能力［1］，在上、下面板之间使用合理布置的圆台形空腔可以实现吸、隔声功能［2］。含空腔点阵增强夹芯结构的芯层由芯材、周期性分布的点阵增强柱及空腔组成，其结构形式复杂，各结构组分的形状、尺寸、材料参数均可影响整体结构的固有振动性能，故难以直接运用经典的层合板理论对其固有振动开展研究。

目前，针对芯层含内部组分的复合材料夹芯结构的振动研究方法，主要包括基于板壳理论的解析方法和有限元方法。王展光等［3］对金字塔点阵夹芯结构的动态力学响应进行了理论分析，其假设面板只承受面内轴力而不承受横向剪力，腹杆承受横向剪力而不承受轴力，从而将点阵夹芯板折算为等效的均质夹层板，采用Reissner夹层板理论，对其在自由振动和简谐载荷作用下的受迫振动问题进行了研究。Lok和Cheng［4］通过将梯形棱柱点阵夹芯板等效为均匀的正交各向异性厚板，采用一阶剪切变形理论，解决了在四边简支边界条件下自由振动和简谐载荷作用时的受迫振动问题。徐胜今等［5］采用Reddy高阶剪切理论，对正交各向异性蜂窝夹层板进行分层研究，推导出了蜂窝夹层板的动力学基本方程，并对正交各向异性单向蜂窝夹层板的自由振动进行深入研究，给出了对边简支时的频率方程和振型函数，同时分析了夹芯厚度及厚跨比对频率的影响。Lou等［6］研究了复合材料四面体点阵夹芯结构的自由振动特性，通过对单胞进行受力分析，求得金字塔点阵芯子的等效横向剪切模量，考虑面板的弯曲变形和芯子的剪切变形，根据哈密尔顿（Hamilton）变分原理推导自由振动控制方程，并求解了固有频率的理论值。朱波等［7］应用ANSYS有限元分析软件，采用8节点Solid 45实体单元，对建立的增强型夹层圆柱壳物理模型进行了自由振动及瞬态动力学过程分析，并考虑树脂材料性能、尺寸和分布等参数变化，分析了点阵增强和齿槽增强对夹层圆柱壳动力学性能的影响。

前人使用的解析方法主要基于成熟的板壳理论，将含内部组分的芯层进行简化等效处理，以方便控制方程的求解，从而对复合材料夹芯结构的振动特性进行分析。该类方法对于芯层内部组分材料相同、尺寸单一且分布形式相似的夹层结构具有一定的普遍适用性，但对于芯层内含2种以上组分，且组分材料不一、尺寸不同的夹层结构，则无法直接适用。

对于多组分复合材料的等效处理研究，Zhu等［8］基于广义自洽法，采用分步均匀化等效的思路，获取了电化学沉积修复饱和混凝土的有效性能。本文将借鉴文献［8］提供的多层次均匀化等效思路，来处理含空腔、点阵增强柱和泡沫基体的复杂芯层的等效问题，并基于一阶剪切变形的夹层板理论，对四边简支含空腔点阵增强夹芯结构的固有振动进行研究。

1 芯层的均匀化等效

含空腔点阵增强夹芯结构由面板和内含多种组分的复杂芯层组成，如图1所示。该夹芯结构的芯层是由芯材、周期性分布的空腔和点阵增强柱组成的3相复合材料。研究夹芯结构固有振动的关键是解决含空腔、点阵增强柱和泡沫基体的复杂芯层的等效问题。本文基于Mori-Tanaka方法，采用多层次均匀化的思路对含复杂组分的芯层进行等效处理。

图1 含空腔点阵增强夹芯结构示意图Fig.1 Schematic diagram of the lattice-reinforced sandwich structure with cavities

1.1 Mori-Tanaka方法

Mori-Tanaka方法是一种基于Eshelby等效夹杂理论求解复合材料等效弹性模量的细观力学方法［9-10］。对于两相夹杂复合材料，其有效模量表示为

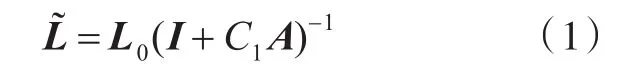
其中，应变集中因子张量A为

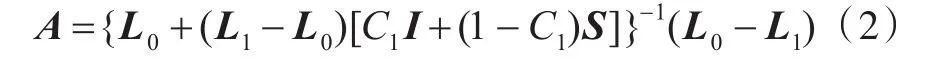
式中：͂为等效后复合材料的弹性常数张量；L0为基体相的弹性常数张量；I为四阶单位张量；C1为夹杂相的体积比；L1为夹杂相的弹性常数张量；S为Eshelby张量，其值由L0和夹杂形状决定。

Zhao等［11］给出了Eshelby张量S的表达式，当夹杂相为圆柱形，材料各向同性，泊松比为ν0时，其Eshelby张量S的矩阵形式可写为

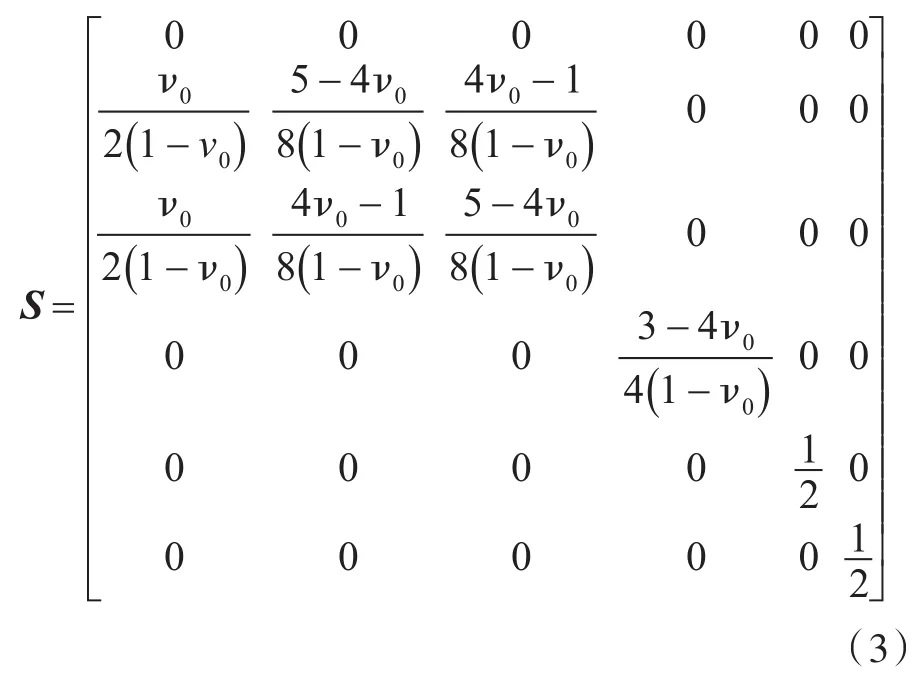
对于正交各向异性（各向同性为其中的特殊情况）材料，式（1）和式（2）中的弹性常数张量L，L0，L1均可表示为以下矩阵形式［12］：

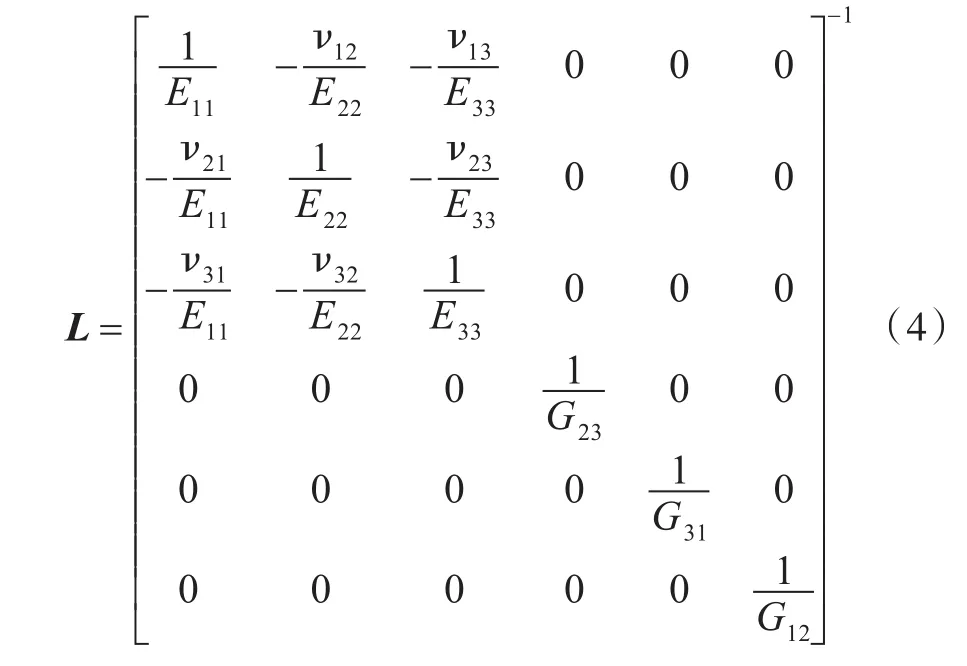
式中：E11，E22，E33分别为弹性主方向上的弹性模量；G12，G23，G31分别为平面内的剪切模量；ν12，ν23，ν13为主泊松比；ν21，ν31，ν32为次泊松比。

将L0，L1的矩阵形式代入式（1）和式（2），可求出复合材料的等效弹性常数张量L͂，对其矩阵形式求逆，就能较方便地得到各个等效弹性模量。

1.2 芯层的等效过程

对于周期性分布的增强柱及空腔的芯层结构，本文采用多层次均匀化等效的思路来获取其等效弹性模量。

1）第1层次等效。

以泡沫芯材作为基体，空腔作为夹杂相，两相复合成为含空腔泡沫芯层。空腔为圆台形，在面内方向上，含空腔泡沫芯层可视作各向同性材料；考虑到本文主要研究的是芯层整体结构的固有振动，可通过体积平均，将圆台形空腔近似视为圆柱形空腔来处理，进一步与芯材基体等效为正交各向异性材料，并记作等效复合材料A，等效过程如图2（a）所示。利用式（1）和式（2），即可求得复合材料A的等效弹性模量。为避免计算过程中出现的奇异问题，将空腔视作一种弹性模量和泊松比都非常小的材料［13］。

采用体积平均方法将圆台形空腔等效为圆柱形空腔，其等效直径为

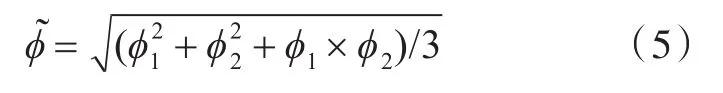
式中，ϕ1，ϕ2分别为圆台形空腔的上、下端直径。

2）第2层次等效。

以等效复合材料A为基体，点阵增强柱作为夹杂相，两相复合进行第2层次的等效。由于增强柱为圆柱形，可以将复合材料等效为正交各向异性材料，并记作等效复合材料B。采用Mori-Tanaka方法，将式（3）和式（4）代入式（1），即可求得正交各向异性等效复合材料B的等效弹性模量。等效过程如图2（b）所示。

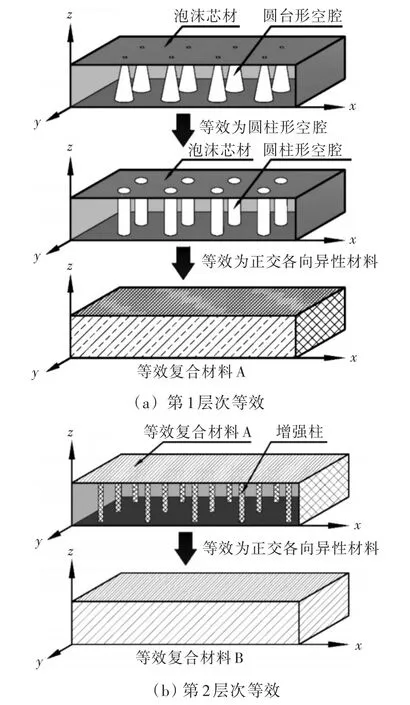
图2 含空腔点阵增强芯层等效为正交各向异性材料的过程Fig.2 Process of the lattice-reinforced core with cavities equalizing to orthotropic material

由上述多层次均匀化等效过程可知，等效复合材料B的模量即可反映含空腔点阵增强芯层的宏观力学性能。

2 一阶剪切变形的层合板理论

取芯层中面作为坐标平面，含空腔点阵增强夹芯结构共 3 层，h0，h1，h2，h3分别为各层厚度，如图3所示。

根据一阶剪切变形的假设，层合板内任意一点在x，y，z方向上的位移u，ν，w可表示为

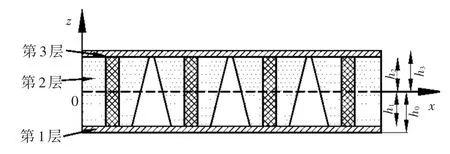
图3 含空腔点阵增强夹芯结构截面示意图Fig.3 Layered section diagram of the lattice-reinforced sandwich structure with cavities

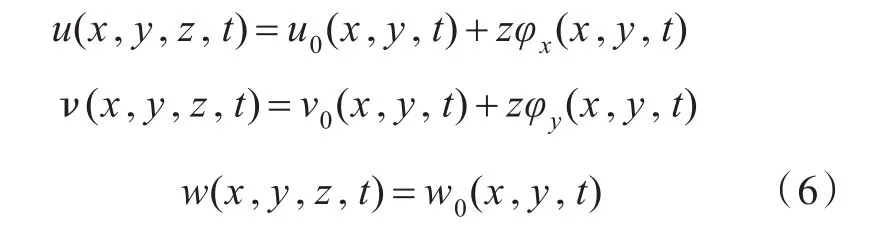
式中：u0(x，y)，ν0(x，y)和w0(x，y)分别为层合板中面上对应位置点在x，y，z方向的位移；φx(x，y)和φy(x，y)分别为法线在x，y方向的转角；t为时间。

根据小变形假设，任意位置处的正应变εx，εy和剪应变γxy，γxz，γyz分别为：

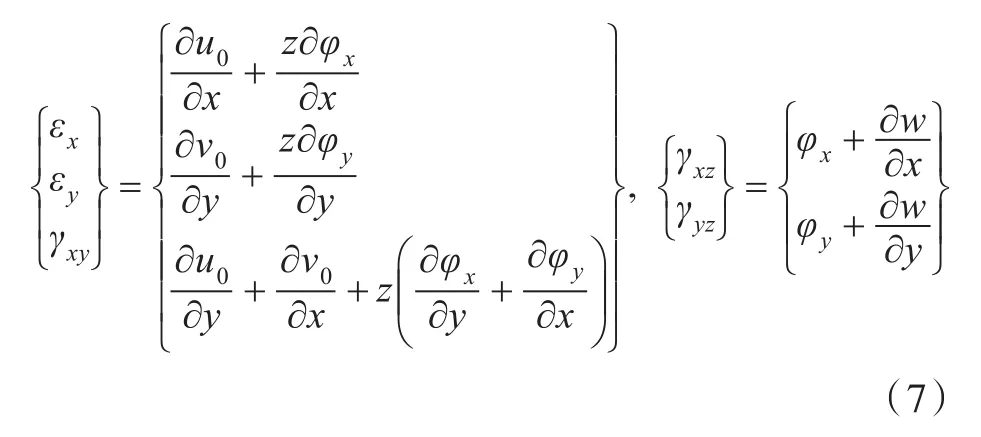
对于正交各向异性材料，应力σx，σy和τxy的应变关系满足下式：

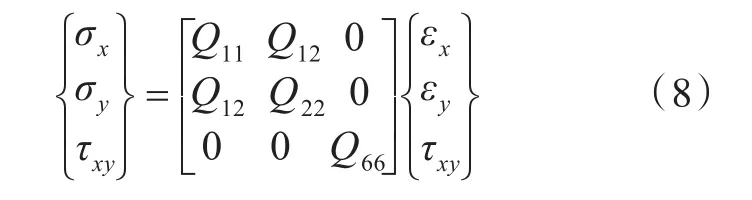
式中，Q11，Q12，Q22和Q66分别为各层的刚度系数，计算公式如下：

截面合力N=（Nx，Ny，Nxy）T及截面弯矩M=（Mx，My，Mxy）T为

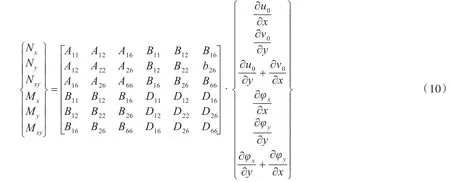
式中，矩阵元素Aij，Bij，Dij是关于Qij及厚度方向坐标z的积分，表达式分别为：

对于一阶剪切变形理论中自由边界上的剪应力不为0的矛盾，此处按照剪切余能相等的原则，假定剪应力在厚度方向呈抛物线分布，进行修正并推导正交各向异性夹层板的剪切刚度为：

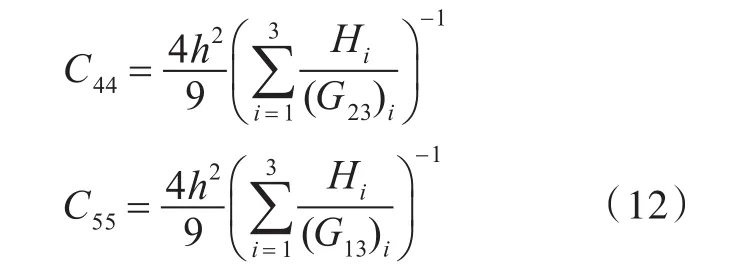
式中：h为层合板总厚度；Hi为中间过程量，

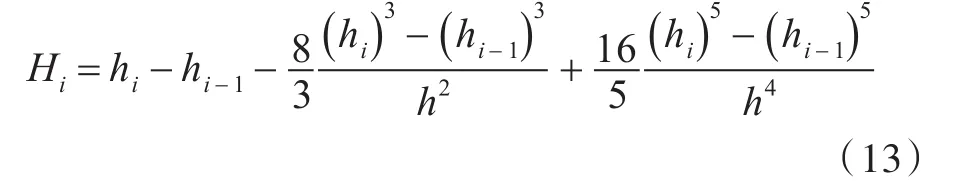
从而夹层板的剪应力可以写为

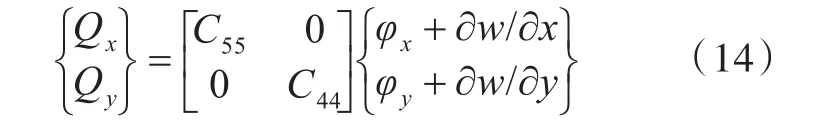
由哈密尔顿原理，可推导出层合板结构真空中的固有振动方程为

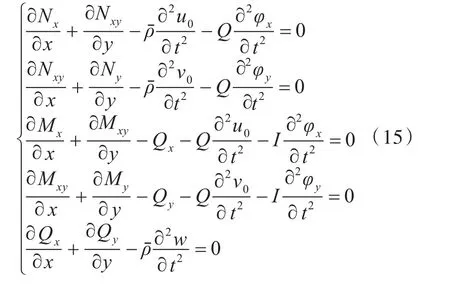
式中：为单位面积层合板的质量；Q为单位面积层合板的分布质量在平动和转动发生耦合时的耦合惯量；I为单位面积层合板的分布质量对所取坐标系的转动惯量，相应的表达式为：

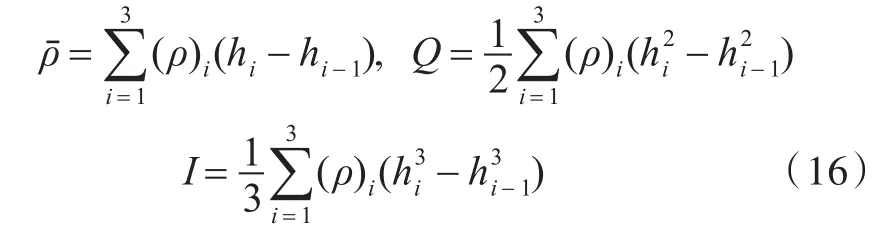
式中，ρ为各层材料的密度。

在四边简支边界条件下，采用双三角级数解法，可对层合板的固有振动方程式（15）进行求解，得到

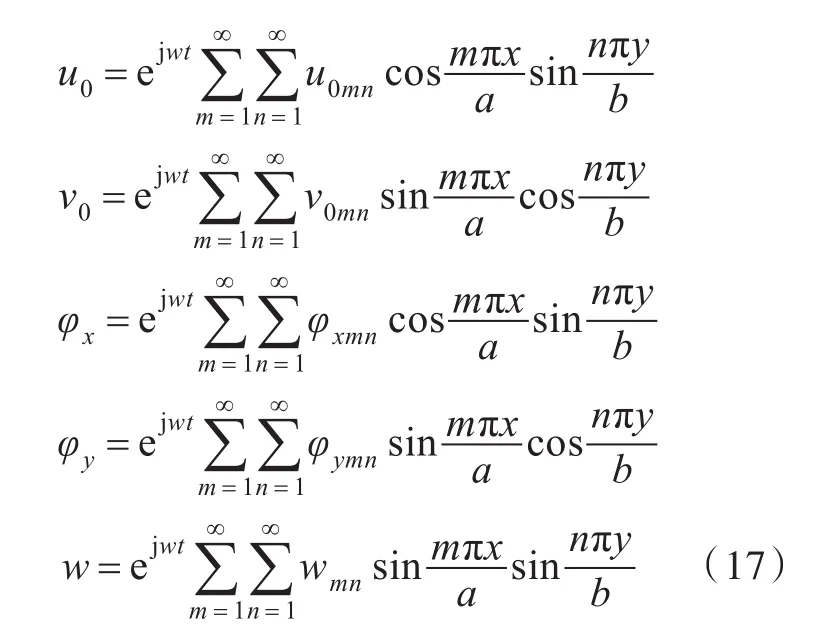
式中：u0mn，v0mn，φxmn，φymn和wmn为广义位移幅值，是待定的值；m和n分别为板振动时在x，y方向的半波数；a，b分别为夹芯板的长度和宽度。取式（17）第m×n项，代入式（16），并在方程两边分别乘上对应的三角函数表达式，利用三角函数正交性解耦，可得到关于广义位移幅值的线性方程组，取该方程组的系数行列式值为0，即可求得各阶模态的固有频率。

3 算例及结果讨论

3.1 算例模型

图4所示为含空腔点阵增强夹芯结构模型的尺寸示意图。图中：c为芯材厚度，f为面板厚度，d为支柱间距，ϕ为增强柱直径，ϕ1，ϕ2分别为圆台形空腔上、下端直径。具体尺寸如表1所示。

由夹杂相的周期性分布规律，取单胞长、宽、厚依次为60，60，40 mm，增强柱体积比RVR为2.18%，空腔的体积比RVC为9.45%。

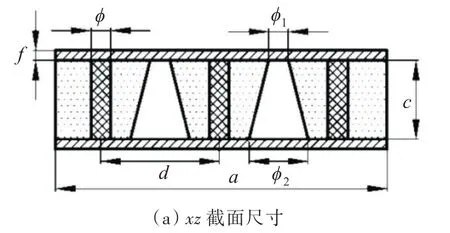
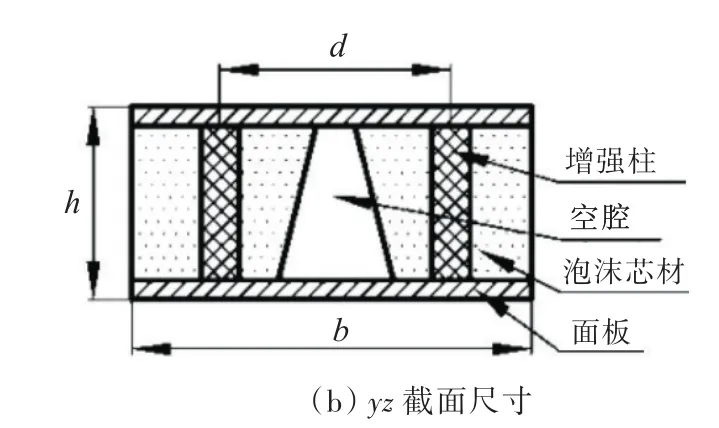
图4 含空腔点阵增强夹芯结构尺寸示意图Fig.4 Schematic diagram of the lattice-reinforced sandwich structure with cavities

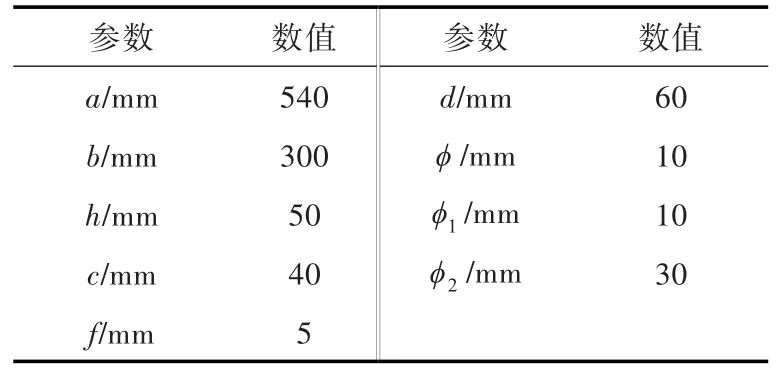
表1 含空腔点阵增强夹芯结构的尺寸参数Table 1 Dimension parameters of the lattice-reinforced sandwich structure with cavities

表2给出了含空腔点阵增强结构使用的材料参数。其中，面板为正交各向异性材料，泡沫芯材和增强柱视为各向同性材料。

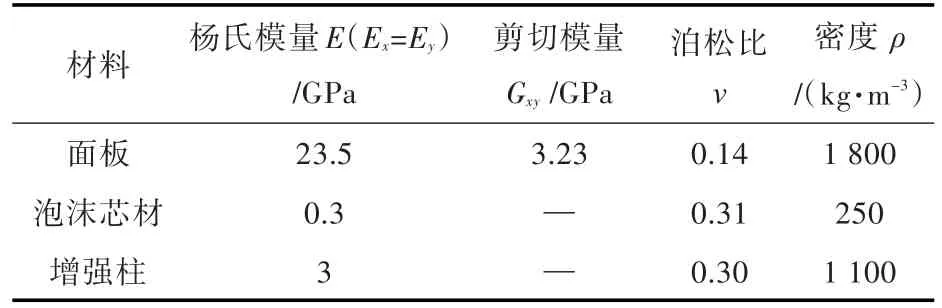
表2 含空腔点阵增强夹芯结构的材料参数Table 2 Material parameters of the lattice-reinforced sandwich structure with cavities

在ANSYS有限元软件中输入正交各向异性材料的材料参数时，3个平面的剪切模量设置为相同的值，厚度方向的杨氏模量Ez也近似用Ex或者Ey代替。

3.2 本文方法与有限元方法对比

采用3.1节的模型尺寸参数，在ANSYS有限元软件中建立含空腔点阵增强夹芯结构的详细模型，图5所示为其局部剖面图。图中，面板采用Shell 181单元，泡沫芯材、增强柱均采用Solid 185单元。划分网格计算至结果收敛，网格数为73 367。计算固有振动频率，并对计算结果进行分析讨论。

对上述夹芯结构进行四边简支约束，计算其在真空中的固有振动，提取前5阶弯曲固有模态结果。表3给出了相应的固有频率。在采用解析法计算的过程中，为避免出现奇异问题，将空腔视作一种弹性模量和泊松比都非常小的材料，通过对空腔弹性模量Ec和空腔泊松比ν0展开收敛性分析，在Ec不大于芯材基体模量的0.001倍（Ec≤0.001Em），同时空腔的泊松比不大于芯材基体泊松比 νm(νc≤ νm)时，满足计算要求。

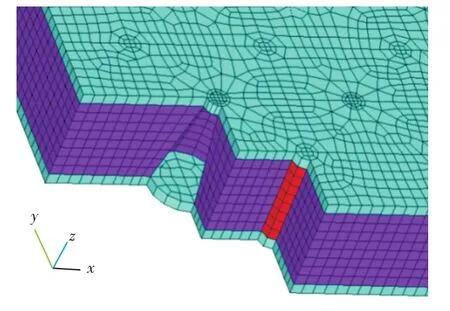
图5 含空腔点阵增强夹芯结构模型局部剖面图Fig.5 Partial section of the lattice reinforced sandwich structure with cavities

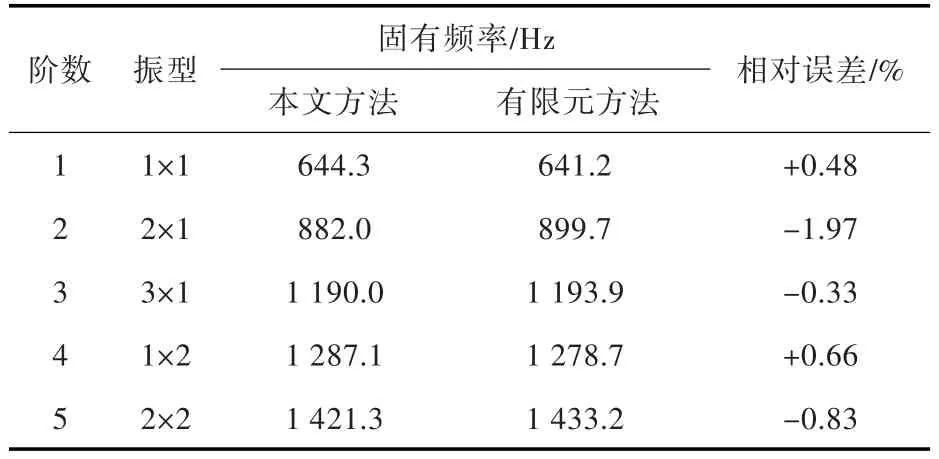
表3 含空腔点阵增强夹芯结构的固有频率Table 3 Natural frequencies of the lattice-reinforced sandwich structure with cavities

从表3中可以看出，本文方法的固有频率解析解与含空腔点阵增强结构详细模型的有限元计算结果吻合得较好，前5阶固有频率的相对误差不超过2%。如图6所示，随着弯曲模态阶数的逐渐增大，当低于40时，固有频率的相对误差基本稳定在6%以内；当上升至40以上时，部分阶数的固有频率的相对误差迅速增大至10%以上。

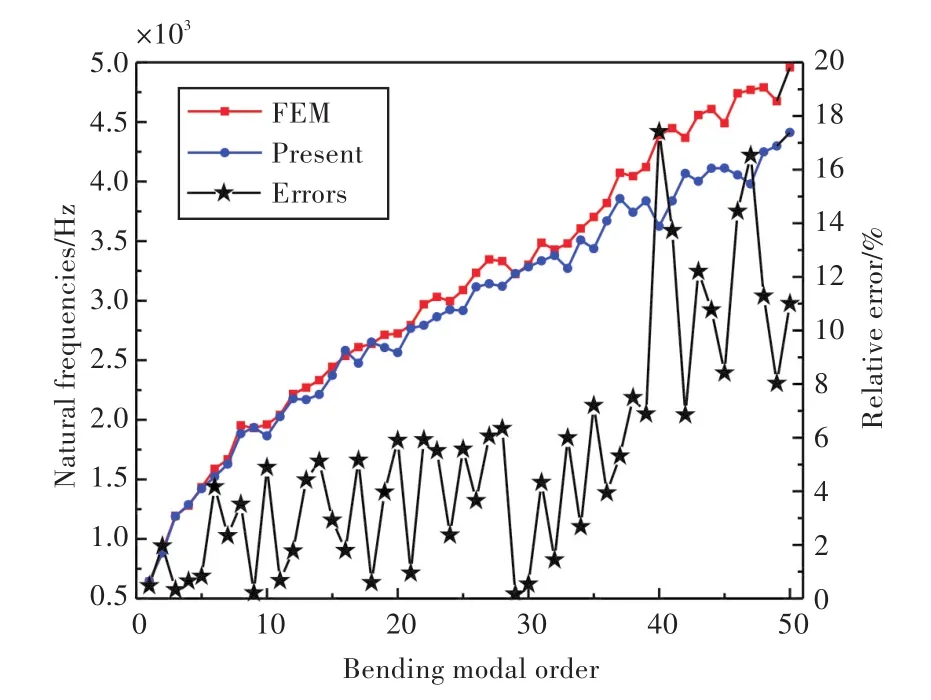
图6 含空腔点阵增强夹芯结构的前50阶弯曲模态固有频率Fig.6 The first 50thorder bending mode natural frequencies of the lattice-reinforced sandwich structure with cavities

表4给出了固有频率相对误差超过10%的部分模态的详细信息。表中，固有频率相对误差较大的模态振型呈现如下规律：半波数在长度方向超过9或在宽度方向超过5。提取第41阶模态（固有频率为3 873.4 Hz）云图分析，并与解析法云图对比，结果如图7所示。当振型半波数为1×6时，模态整体基本相似，但含空腔点阵增强结构的有限元云图出现了明显的局部模态特征。其他固有频率相对误差大于5%的模态阶数对应的云图也表现出了类似的特征。

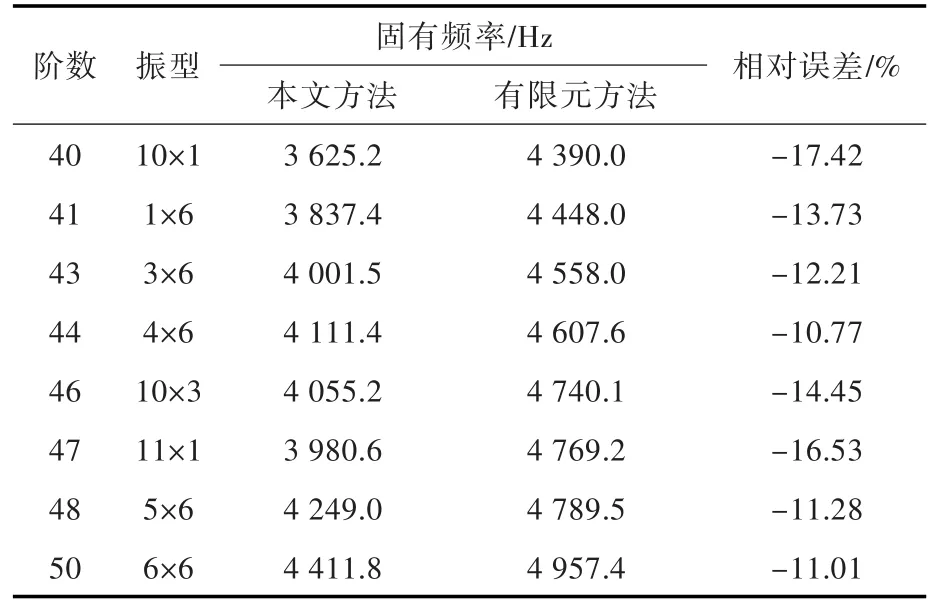
表4 相对误差超过10%的部分模态详细信息Table 4 Details of some modes with relative error exceeding 10%

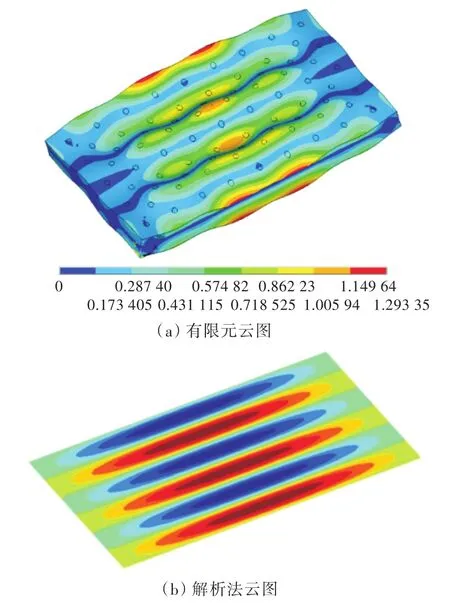
图7 含空腔点阵增强夹芯结构等效模型第41阶模态Fig.7 The 41thmode of the lattice-reinforced sandwich structure with cavities

结合上述分析，考虑到本算例中含空腔点阵增强夹芯结构的内部周期性分布了9×5个增强柱和8×4个空腔，可以总结得出，在模态振型半波数超过对应方向的内部夹杂结构数量时，增强柱和空腔的局部模态对实际夹芯结构的整体模态影响较大，导致本文采用解析法和有限元方法得到的固有频率的相对误差快速增大；而对于前40阶模态，在模态振型半波数不超过对应方向的内部夹杂结构数量时，增强柱和空腔的局部模态对含空腔点阵夹芯结构的整体模态影响较小，夹芯结构的振动主要以整体模态为主，此时本文采用解析法与有限元方法得到的结果吻合较好。

以上中、低频固有振动的计算结果表明，本文采用多层次均匀化等效Mori-Tanaka方法，将包含空腔、点阵增强柱和泡沫基体的复杂芯层结构等效为正交各向异性材料，并基于一阶剪切变形夹层板理论，计算四边简支含空腔点阵增强夹芯结构的中、低频固有频率时具有良好的适用性和准确性。

3.3 芯材面板模量比Em/Ep对含空腔点阵增强芯层等效弹性模量的影响规律

芯层尺寸及材料参数同3.1节，保持芯材模量Em不变，改变面板模量Ep，求不同芯材面板模量比Em/Ep下含空腔点阵增强夹芯结构的固有频率。图8所示为前5阶结果。

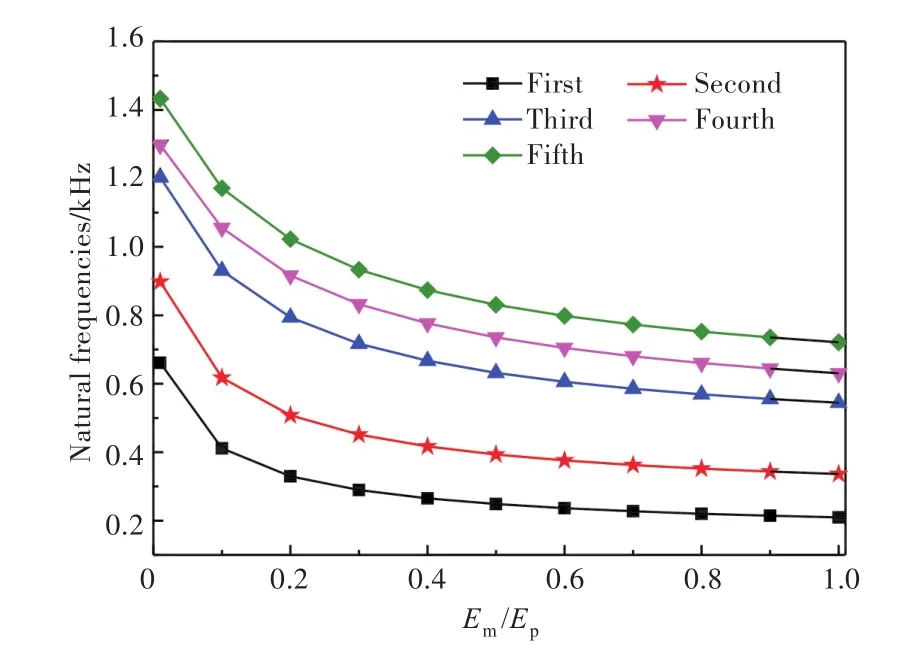
图8 含空腔点阵增强夹芯结构固有频率随芯材面板模量比Em/Ep的变化关系Fig.8 Relation between natural frequencies of the latticereinforced sandwich structure with cavities andEm/Ep

由图可以看出，当芯材模量Em不变时，随着芯材面板模量比Em/Ep的增大，各阶固有频率均呈下降趋势；当芯材面板模量Ep较小时，各阶固有频率随着芯材面板模量比Em/Ep的增大而减小较快，即当芯材与面板模量相比较为悬殊时，芯材面板模量比Em/Ep对含空腔点阵增强夹芯结构固有频率的影响较大。

3.4 增强柱体积比RVR对含空腔点阵增强夹芯结构固有频率的影响规律

芯层尺寸及材料参数同3.1节，改变点阵增强柱直径，采用本文解析方法，求不同增强柱体积比RVR对应的含空腔点阵增强夹芯结构的固有频率。图9所示为前5阶结果。

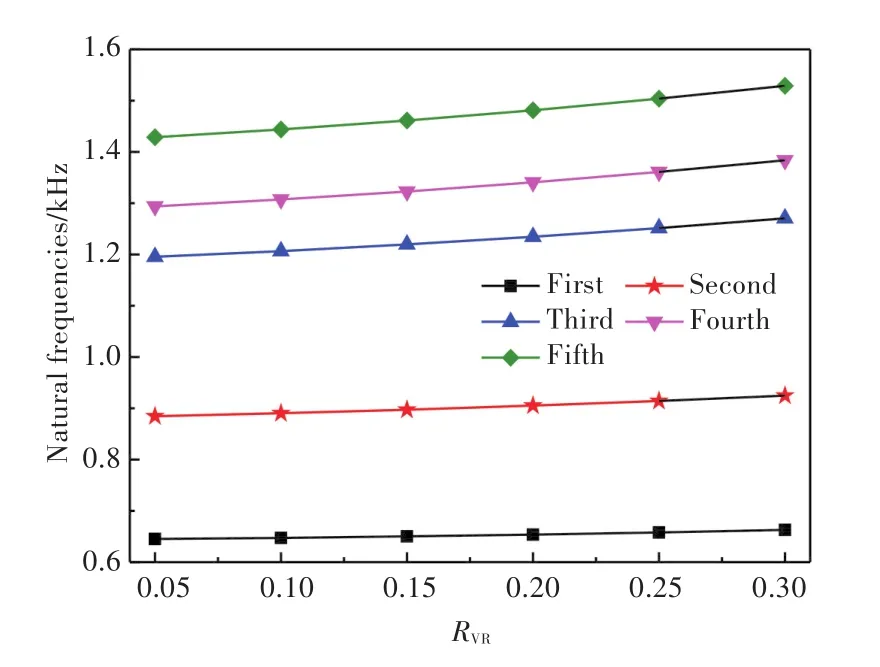
图9 含空腔点阵增强夹芯结构固有频率随增强柱体积比RVR的变化关系Fig.9 Relation between natural frequencies of the latticereinforced sandwich structure with cavities and RVR

由图可以看出，随着增强柱体积比RVR的增大，各阶固有频率均逐渐增大，但增大的趋势较小。这说明增强柱对整体结构的中、低频固有频率的影响较小。

3.5 空腔体积比RVC对含空腔点阵增强芯层等效弹性模量的影响规律

芯层尺寸及材料参数同3.1节，保持点阵增强柱直径ϕ=10 mm不变，改变空腔体积，求不同空腔体积比RVC对应的含空腔点阵增强夹芯结构的固有频率。图10所示为前5阶结果。

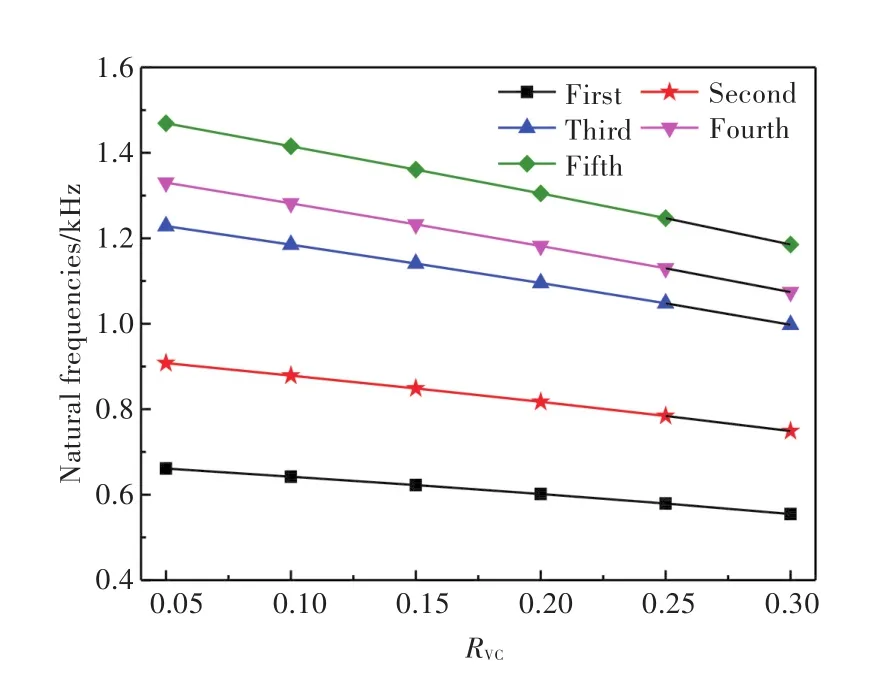
图10 含空腔点阵增强夹芯结构固有频率随空腔体积比RVC的变化关系Fig.10 Relation between natural frequencies of the latticereinforced sandwich structure with cavities and RVC

由图可以看出，随着空腔体积比RVC的增大，各阶模态的固有频率几乎呈线性下降，同时减小的趋势较明显。这说明空腔体积比对整体结构的固有频率的影响较大。

4 结 论

本文采用多层次等效的思路处理结构复杂的芯层，并基于一阶剪切变形夹层板理论研究了四边简支含空腔点阵增强夹芯结构的固有振动特性，得出如下结论：

1）采用多层次均匀化等效的Mori-Tanaka方法处理含空腔点阵增强结构的复杂芯层是适用的，芯层结构的等效弹性模量可以用于预测含空腔点阵增强结构的中、低频固有频率。

2）基于一阶剪切变形理论，计算四边简支含空腔点阵增强夹芯结构得到的中、低频固有频率的误差不超过3%，可满足工程精度要求，且数理模型清晰，计算速度快，便于固有振动特性的规律研究。

3）芯材面板模量比、点阵增强柱体积比和空腔体积比对含空腔点阵增强夹芯结构的固有频率均有一定的影响，当芯材与面板模量之比较小时，芯材面板模量比对含空腔点阵增强夹芯结构固有频率的影响较大。

对于中、高频振动，即模态振型半波数大于对应方向的内部夹杂结构数量时，固有频率的误差增大较快，本文方法将不再适用。将考虑采用板—杆耦合振动的思路来开展下一步的研究，并通过模型试验进行验证和修正。