干式超声清洗变截面空腔流场特性仿真分析

刘福来，张 波，赵 恒，隆志力﹡

(1. 河南科技大学机电工程学院，河南 洛阳 471003；2. 哈尔滨工业大学(深圳)机电工程与自动化学院，广东 深圳 518055)

1 引言

在液晶显示器和半导体制造工艺流程中，清洗的效果直接影响成品的各项指标，因此清洗除尘工艺在整个显示器和半导体生产线中起着重要的作用[1]。目前，干式超声波清洗已经成为半导体显示器除尘最为有效的新型技术。相比于传统的湿式超声波清洗[2]，干式超声波清洗在我国尚属开始研究阶段，当前研究深度与广度尚存不足[3，4]。干式超声波清洗的优点在于：不需要另加清洗剂，绿色环保；非接触式清洗，避免被清洗件损害；无附加风干设备，成本较低；对于1.6μm 以上的尘粒去除率接近100%[5]。

干式超声波清洗系统包括空气循环系统、被清洗件传送系统和超声清洗头三大部分。变截面空腔是干式超声清洗头的核心部件，也是使高速气流转变为高频波动的关键结构[6]。因此，国内外学者对变截面空腔结构开展广泛研究。Yun E J等[7]通过在出口增加喇叭形放大器，降低了超声波传播能耗。Choi H等[8]通过改变空腔结构以增加流速并对不同粒径微粒运动轨迹进行了比较。庞浩斐等[9]对超声干式清洗技术进行了理论分析与仿真。Liu Y H[10]等研究了干冰喷射去除附着在表面上的细颗粒的应用，并考察了去除过程。Yin Z Y[11]等设计了一种利用换能器代替机械动态结构产生超声波的空腔结构。侯中喜，易仕和等[12]对影响空腔内流场特性的因素进行了研究。Worapol T等[13]基于谐波响应分析的工业超声波清洗槽的研制。马明生等[14]讨论了空腔长深比对空腔流场特性的影响。

综上所述，目前研究均未对影响空腔出口流场特性的因素进行对比分析。本文通过对可压缩Navier-Stokes方程做Favre滤波化简整理得到任意曲线坐标下的大涡模拟方程(LES)，利用流体仿真软件ANSYS Fluent17.0建立变截面空腔流场计算模型。通过对不同空腔长深比、腔口长度(H)、入口气流速度与空腔组数等关键因素对变截面空腔出口流场特性的影响分析研究。设计出了一种腔口流场特性最优的变截面空腔，其研究结果为微粒再悬浮及悬浮后运动轨迹的研究提供技术参考。

2 变截面空腔设计与数值分析

2.1 结构设计

本文设计了一种变截面空腔结构包括：入口(inlet)，出口(outlet)，其余为壁面(wall)，如图1所示。通过Fluent流体仿真软件模拟仿真出影响变截面空腔腔口流场特性的因素，并应用得出的变截面空腔结构参数设计了一种干式超声清洗头，如图2所示，其包括第一真空腔、第二真空腔、储压加速腔和变截面空腔。高速气流从储压加速腔的进口通入，再次加速后的气流通过变截面空腔形成高速超声波气流并从腔口吹向被清洗基板，结构两侧的第一真空腔和第二真空腔将被高速超声波气流吹起的悬浮微颗粒吸入并进行分离。

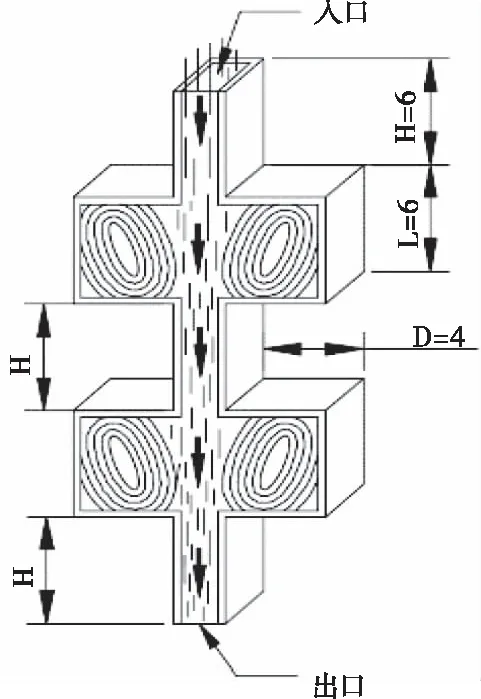
图1 变截面空腔结构图

图2 干式超声清洗头结构及原理图

2.2 跨声速流体方程

将亚声速或超声速的高速气流通过变截面空腔，因此需要将通入变截面空腔的气体作为可压缩流体。直角坐标轴系下的N-S方程组包含连续性方程、动量方程和能量方程，采用守恒形式下的方程组可表示为

(1)

式中A为守恒矢变量，B，C，D为无粘矢通量，Bv，Cv，Dv为粘性矢通量，S为源项，ρ为密度，u，v，w分别为流体在x，y，z方向上的速度，e为流体总能，qi为热流量。

设任意曲线坐标系下的坐标变量为

ζ=ζ(x，y，z)，η=η(x，y，z)，ς=ς(x，y，z)

(2)

定义坐标变换为

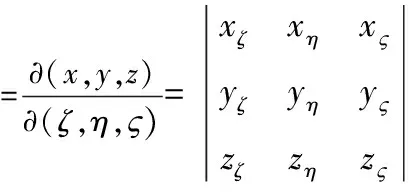
=xζ(yηzς-yςzη)-xη(yζzς-yςzζ)+xς(yςzη-yηzζ)

(3)

Favre滤波通过过滤函数(4)来实现

(4)

整理得到任意曲线坐标下的可压缩流动LES主导方程为

(5)

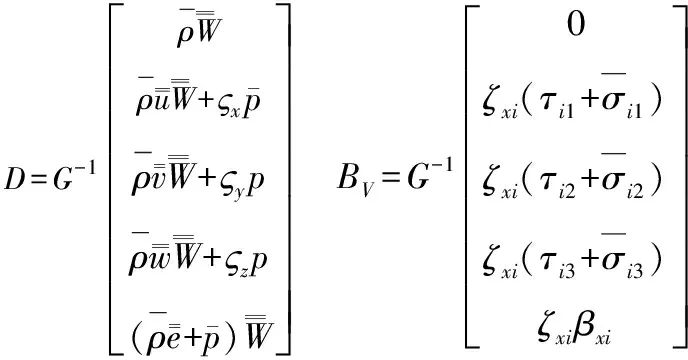
3 空腔流场仿真分析

3.1 仿真平台及其参数设置

ANSYS Fluent17.0是一款应用于流体、热传递和化学反应等有关问题的仿真分析计算软件。本文应用该软件的流体功能模块，采用得出的可压缩流动方程(LES)，双精度求解器(Double Precision)，非定常瞬态分析(Transient)，二阶隐式(Second Order Implict) 离散格式，PISO压力-速度耦合算法，PRESTO！压力插值方案，对变截面空腔内的空气介质流体进行网格划分。入口速度设置为300m/s，压力为15kPa，出口静压为0，亚松弛因子Pressure和Momentum分别为0.3和0.7，时间步长设为5×10-5，步数设为1000。

3.1.1 空腔内流场仿真结果分析

为了研究不同空腔腔口流场特性的影响因素，本文对设计的标准空腔内流场做仿真分析，其设置参数为：入口气流速度为300m/s，空腔长深比为1.5，空腔组数为2组以及腔口长度为 6mm。分析此变截面空腔内的流场分布，得到t=0.1s时刻变截面空腔内的速度和压力流场仿真云图，如图3所示。从流场云图可直观反映出空腔内压力和速度的状态。

图3 变截面空腔内流场云图

从图3(a)速度云图可知，气流在从腔口前缘流至腔口后缘的过程中空腔中心速度最高，随着气流的稳定，空腔内因速度不均从前缘形成脱落涡，运动到空腔后缘并与空腔后缘发生碰撞，从而形成空腔的流激振荡。从图3(b)压力云图可知，因经过空腔流道气流速度的增加，使空腔流道压强从入口到出口逐渐降低，空腔出口处甚至可能出现负压现象。

3.2 腔口流场仿真结果分析

表1为空腔长深比、入口气流速度、空腔组数和腔口长度等不同参数形式，按照其各参数形式进行变截面空腔出口流场特性仿真分析。所有空腔仿真数据设定均与3.1节一致。

表1 变截面空腔结构及参数

3.2.1 入口气流速度对腔体出口流场的影响

由3.1.1节的分析可知，空腔出口中心气流速度变化最能突出腔口流场特性，因此本文对不同因素下腔口中心瞬时气流速度进行了分析对比。选择表1-1中Ⅰ所示的参数进行仿真，入口来流速度分别为200m/s、250m/s、300m/s和350m/s。图4(a)为腔口中心速度随时间的变化曲线，图4(b)为腔口中心气流频率与振幅变化曲线。

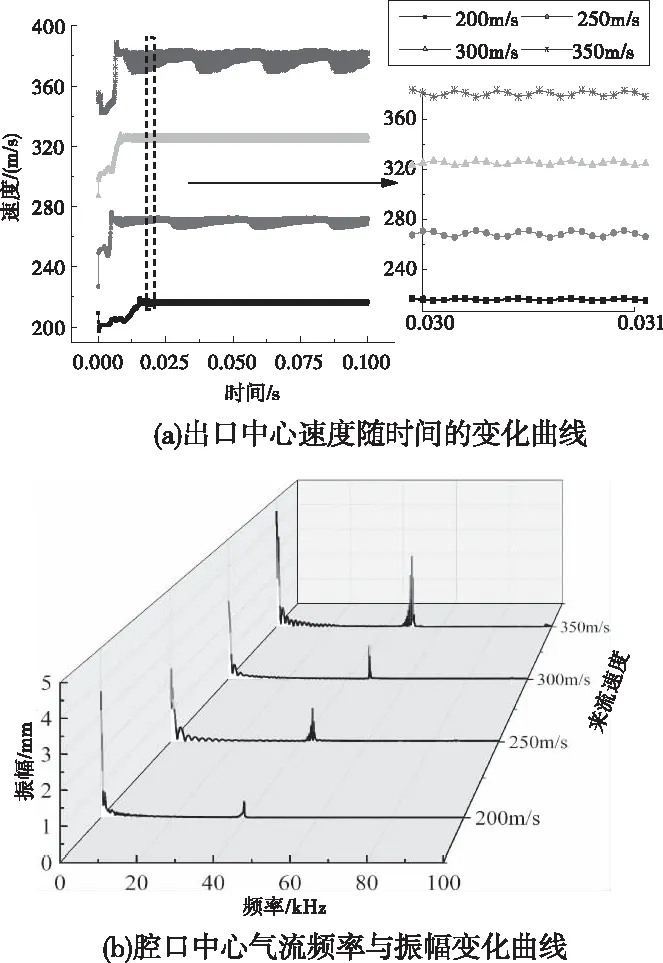
图4 入口气流速度对腔口流场特性的影响

从图4(a)中可看出，当入口气流速度越大时，空腔出口气流达到稳定的时间就越短，且随着入口气流速度的增大，腔口速度也随之增大。从图4(b)中可以看出，随着入口气流速度的增大，腔体出口的气流波动就越平稳，但气流速度过大，腔体出口的气流波动会不平稳。不同入口气流速度下，在40kHz左右时，腔体出口气流振幅会出现耦合，耦合振幅过大或过小均不能使被清洗基板上的微粒再悬浮，而在1-3mm时最有利于微粒的悬浮清洗。综上，入口气流速度过大和过小均对腔口气流速度增幅及不同频率下振幅均有较大影响，不利于干式清洗。

3.2.2 空腔长深比对腔体出口流场的影响

空腔长深比是影响变截面空腔出口流场特性的重要因素之一。选择表1-1中参数Ⅱ所示的四种不同空腔长深比结构，设置入口气流速度300m/s，空腔长深比分别为L/D=1、L/D=1.2、L/D=1.5和L/D=2。图5(a)为腔口中心速度随时间的变化曲线，图5(b)为腔口中心气流频率与振幅变化曲线。

由图5(a)可看出，相同入口气流速度下，随着空腔长深比的增大，腔口速度均有增幅，长深比为1.5和2时增幅最为明显。从图5(b)中可以看出，腔口气流波动振幅随着空腔长深比的增加而增大，长深比为1.5时，在40kHz左右，腔体出口气流振幅会出现耦合，且耦合振幅适中。综上，空腔长深比过小时腔口速度增幅不明显，空腔长深比过大时腔口气流波动不稳定，只有在合适的空腔长深比下腔口速度的增幅大且气流波动振幅平稳。

图5 空腔长深比对腔口流场特性的影响

3.2.3 腔口长度对空腔出口流场的影响

如图2，选择表1-1中参数Ⅲ所示的三种腔口长度(H)的矩形空腔结构进行仿真分析，腔口长度(H，单位：mm)分别为H=3、H=6和H=12。图6(a)为腔口中心速度随时间的变化曲线，图6(b)为腔口中心气流频率与振幅变化曲线。

由图6(a)看出，相同入口气流速度和空腔长深比下，腔口速度增幅随着腔口长度(H)的增加而增加，但腔口速度增幅越低以及达到稳定所用的时间却越长。从图6(b)中可以看出，腔口长度(H)分别为H=3mm和H=6mm时振幅最稳定，但H=3mm时没有明显耦合现象。综上，随着腔口长度(H)的增加，腔口速度增幅会降低，但达到稳定所用时间会越短，在不同频率下，腔口长度(H)过短或过长均会影响空腔的速度增幅和振幅波动的稳定性。

图6 腔口长度对腔口流场特性的影响

3.2.4 空腔组数对空出口流场的影响

分别选用相同长深比、入口气流速度和腔口长度(H)，选择表1-1中参数Ⅳ所示的包含一组、二组和三组的矩形空腔。图7(a)为腔口中心速度随时间的变化曲线，图7(b)为腔口中心气流频率与振幅变化曲线。

图7(a)表明，在其它因素相同的情况下，随着空腔组数的增加，腔口速度增幅会有提高，但是空腔组数的增加会影响腔口流场波动特性，从整体来看虽是规律性波动，但局部时间段内波动不均匀。当空腔结构为一组、二组空腔时，腔口流场波动较为均匀，二组空腔时，腔口速度增幅更高。从图7(b)中可以看出，不同频率下空腔组数为一组和三组的腔口流场振幅波动不均匀。综上，当变截面空腔的空腔组数为2组时，腔口的速度增幅最高，振幅波动最平稳。

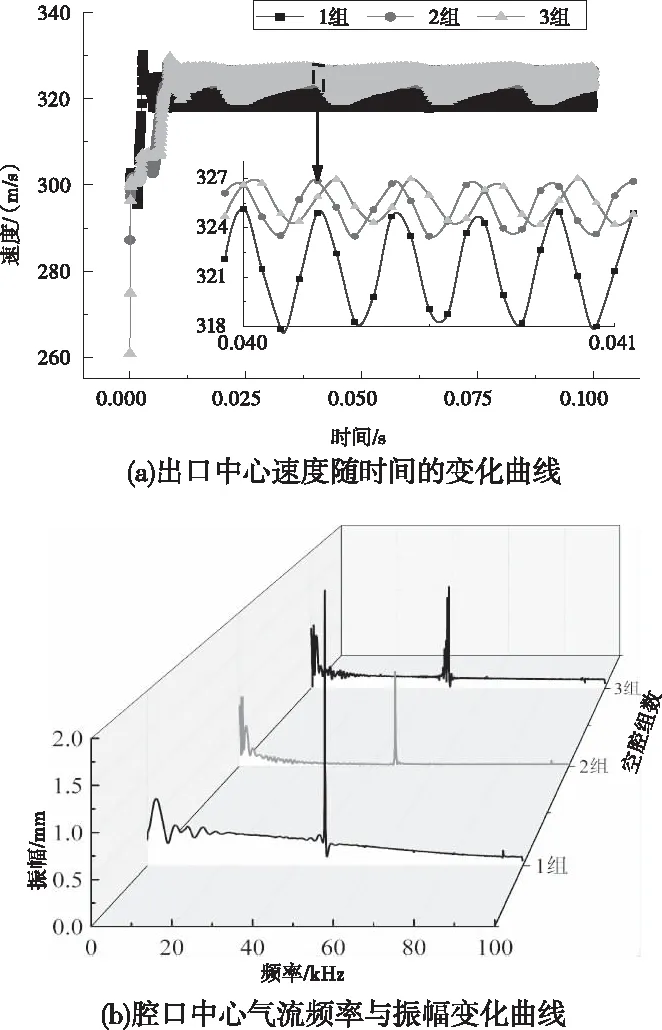
图7 空腔组数对腔口流场特性的影响

4 结论

1)通过计算仿真设计了一种空腔出口流场最优的变截面空腔结构，其参数为：空腔长深比为1.5、入口气流速度为300m/s、空腔组数为2组以及腔口长度为 6mm；应用所得变截面空腔设计了一种能够产生超声频流场的干式超声清洗头。

2)变截面空腔长深比和入口气流速度对腔口流场特性影响最大，空腔长深比和入

口气流速度过大或过小均会影响变截面空腔出口气流达到稳定的时间、速度增幅以及不同频率下的振幅波动。

3)经过滤波得到的大涡模拟方程能够分析计算变截面空腔的可压缩气流场特性，分析得出的空腔结构参数为干式超声清洗系统的研究提供了理论依据，验证了有限元仿真方式能够应用于跨声速流场的仿真研究。