偏转工况下吊舱推进器的水动力和空泡性能

李善成，熊鹰，王展智

海军工程大学舰船与海洋学院，湖北武汉430033

0 引 言

吊舱推进器集操舵与推进功能于一体，可以完成船舶回转操作。当吊舱推进器发生偏转时，其承受的载荷将有所增加，水动力和空泡性能将随之恶化，因此研究吊舱推进器在偏转工况下的水动力和空泡性能至关重要。目前，在敞水性能实验和数值预报方面，国内外学者已开展了大量工作，并取得了诸多成果［1-4］。Szantyr［5］基于空泡水筒对吊舱推进器在斜流工况下的水动力性能开展了实验研究，并测量了推进器的推力和横向力。Liu等［6］研究了吊舱推进器在偏转工况下的水动力性能，详细分析了螺旋桨的推力和扭矩变化情况。Amini等［7］采用势流和粘流方法计算了吊舱推进器在不同偏转角下的轴承力。熊鹰等［8］、王展智等［9］和沈兴荣等［10］基于雷诺平均（Reynolds Average Navier-Stokes，RANS）数值模拟方法分析了吊舱推进器在不同舵角工况下的水动力性能，实验对比结果表明，采用RANS方法结合结构化网格可以准确预报吊舱推进器的水动力性能。在空泡方面，Friesch［11］针对典型的拖式吊舱推进器开展了空泡实验，结果表明，在一定角度下增加螺旋桨的载荷时，其空泡性能将出现明显变化；当吊舱偏转方向不同时，其空泡密度也有所不同。杨晨俊［12］对第25届ITTC吊舱推进专家委员会的报告内容予以了总结，建议在吊舱推进器实验方面重点关注非设计工况下的敞水特性，尤其是小舵角导致的推进效率损失问题。综上所述，目前的研究成果主要集中在偏转工况下吊舱推进器的水动力性能和空泡变化的观测实验方面，尚未针对吊舱推进器偏转后的桨叶载荷变化和吊舱桨空泡性能开展深入的研究工作。然而，偏转工况下吊舱推进器的桨叶载荷发生剧烈变化，其空泡性能也将随之恶化，剧烈的空泡会导致推进器效率降低、桨叶材料剥蚀，因此研究偏转工况下吊舱推进器的水动力性能和空泡性能具备一定的工程应用价值。

本文拟基于吊舱推进器的水动力性能预报成果，分析吊舱桨在偏转工况下的桨叶压力分布变化情况，并采用Sauer空泡模型预报吊舱推进器的空泡性能，最后，将在空泡水洞中开展吊舱推进器偏转工况下的敞水和空泡实验，以验证数值预报方法的准确性。

1 研究对象

本文以1∶25的缩尺比推进器实验模型为研究对象，图1所示为吊舱体模型，图2所示为吊舱体的几何示意图，表1和表2分别为螺旋桨与吊舱体的主要参数。

图1 吊舱体模型Fig.1 Model of pod body

图2 吊舱体的几何示意图Fig.2 Geometric diagram of the pod body

表1 螺旋桨的主要参数Table 1 Main parameters of propeller

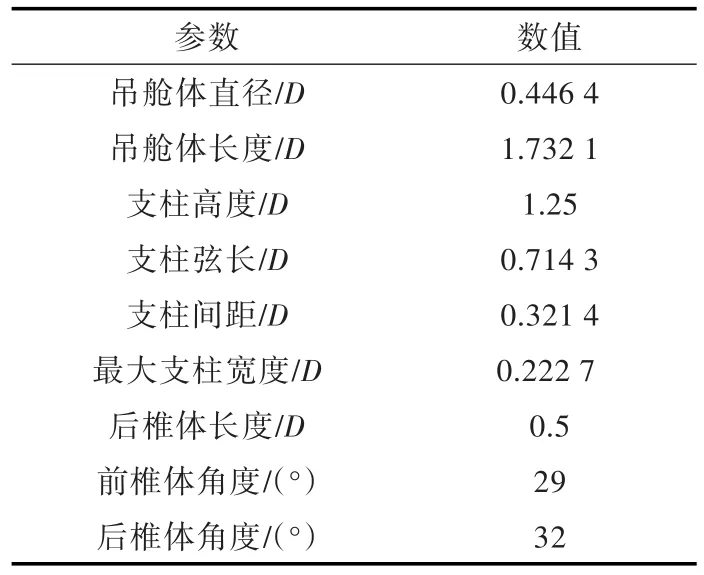
表2 吊舱体的主要参数Table 2 Main parameters of pod body

2 数值方法

2.1 控制方程

RANS方程为：

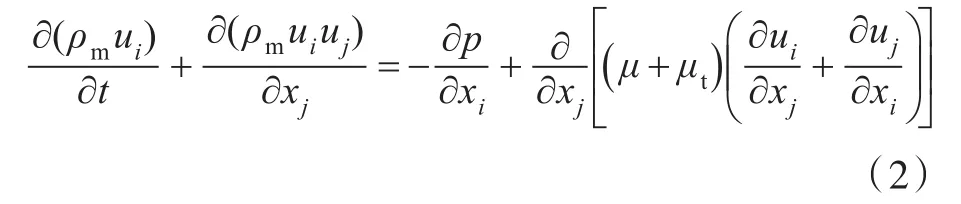
式中：ρm为混合相密度，其中混合相由水的液相和汽相组成，且假定2个混合相的速度相同；t为时间；ρ为流体密度；xi和xj（i，j=1，2，3）为三维笛卡尔坐标系下的方向坐标；ui和uj为流体速度在xi和xj方向的分量；p为流体微元体上的压力；μ为混合相粘度；μt为混合相湍流粘度。

水动力性能即液相特性，为便于计算，本文将采用SSTk-ω两方程模型［13］作为湍流模型。该模型引入了混合函数，以结合求解近壁区流动的Standardk-ω模型和求解远场流动的Standardk-e模型。

2.2 空泡模型

在计算空泡性能时，ρm为汽液混合相密度，其值由汽相体积分数v决定：

式中，ρl和ρv分别为液相和汽相的密度。

假设汽相在液相中以气泡的形式存在，其输运方程为

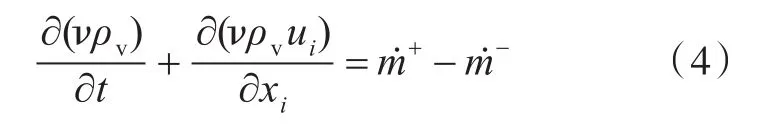
式中：+为液相至汽相的蒸发率；-为汽相至液相的凝结率。

Sauer建立了+和-的表达式［14］，即

式中：R0为气泡半径；pv为饱和蒸汽压力。

2.3 计算域及网格划分

均匀流场计算域由远场域和桨旋转域组成，如图3所示。其中，前方和四周为速度入口，前方入口距离桨中心5D，截面面积为6D×6D，压力出口距离桨盘面12D。计算水动力性能时，将采用网格生成软件ICEM划分全域六面体结构网格，总网格数约为3.5×106。本文将采用商业数值计算软件STAR-CCM+，首先采用动参考系法对吊舱推进器进行定常计算，待收敛后再采用非定常方法加快收敛进程。其中，仿真时间步长为螺旋桨旋转1°所对应的时间，水动力计算选用RANS结合SSTk-ω模型。来流速度为3 m/s，可以通过改变转速来改变进速系数。

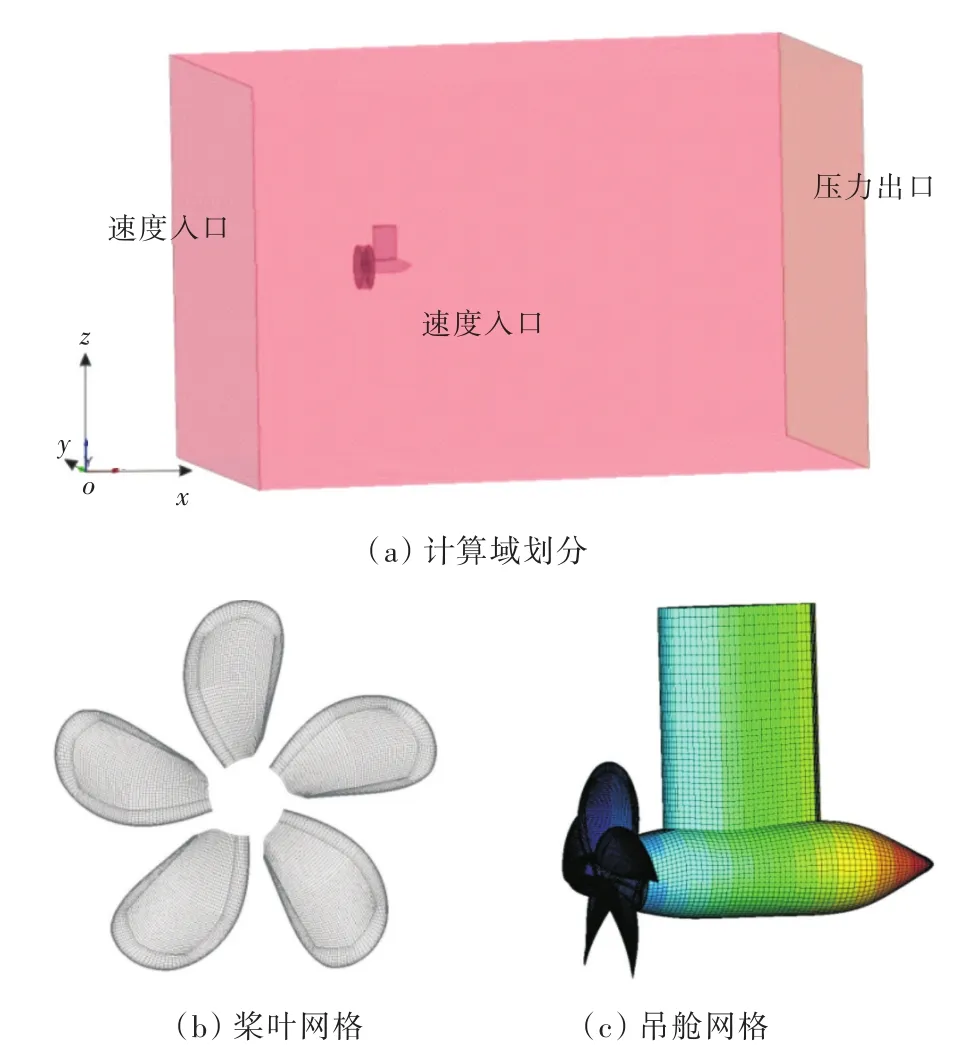
图3 计算域和网格划分Fig.3 Computational domain and mesh generation

计算空泡性能时，需要对吊舱和桨叶（尤其是叶梢部分）网格进行加密，总网格数为6×106。首先采用动参考系法进行定常计算，然后进行非定常计算，并逐步降低环境压力以达到空泡数量要求，待收敛后再采用空泡模型进行计算。其中，时间步长为螺旋桨旋转1°所对应的时间，空泡模型选用Schnerr-Sauer模型。来流速度为3.3 m/s，出口压力与实验环境一致。

吊舱的偏转角、螺旋桨的推力T和扭矩Q的定义如图4所示。从船艉看向船艏时，吊舱偏转角为β，向左偏转为负，向右偏转为正；桨叶正对着吊舱体支柱时，桨叶周向角θ=0°。

图4 吊舱推进器的水动力性能参数、偏转角、周向角及参考系Fig.4 The hydrodynamic performance parameters，deflection angle，circumferential angel and coordinate system of podded propulsion

在计算过程中，改变来流方向即可实现吊舱偏转，其中速度入口处的水流为

式中：Vx为叶剖面处来流的轴向速度；Vy为叶剖面处来流的横向速度；U为来流速度；J为进速系数；n为螺旋桨转速。

3 实验方法

实验布置如图5所示，其中空泡水筒的尺寸为：长2.6m，宽0.6m，高0.6m。本实验采用CASSIONS公司的H101动力仪，其推力量程为±600 N，扭矩量程为±30 N·m，最大转速为3 000 r/min。在实验过程中，通过偏转吊舱动力仪即可实现吊舱推进器的舵角偏转。

图5 实验布置图Fig.5 The arrangement of model test

3.1 敞水实验

为保证雷诺数满足敞水实验要求，来流速度均设定为3 m/s。在实验过程中，通过改变螺旋桨转速即可改变进速系数。空泡水筒实验应满足的雷诺数条件为

式中：Rn(0.75R)为螺旋桨0.75R处的雷诺数，其中R为螺旋桨半径；b0.75R为0.75R处的叶切面弦长；ν′为水的运动粘性系数。

推力系数KT和扭矩系数KQ的计算公式为：

3.2 空泡观测实验

空泡观察实验中，设定来流速度为3.3 m/s，螺旋桨转速为1 254 r/min，空泡数σn=1.44。

空泡数的表达式为

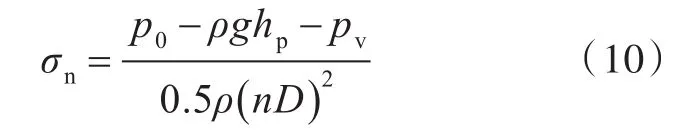
式中：p0为循环水筒工作段中心处压力，取值为0.22个标准大气压；g为重力加速度；hp=0.3 m，为螺旋桨模型中心与吊舱推进器工作段中心线的垂直距离；pv=2.338×103Pa。

4 结果分析

4.1 水动力性能分析

4.1.1 吊舱螺旋桨的水动力性能分析

1）网格无关性分析。

在水动力计算的基础上，选取J=0.64，在直航和偏转+10°工况下进行网格无关性分析。在表3所示的3套网格方案中，近壁面网格沿壁面法向的划分方法相同，而螺旋桨旋转域的网格数量有所不同，其推力系数和扭矩系数的计算结果如表4所示。

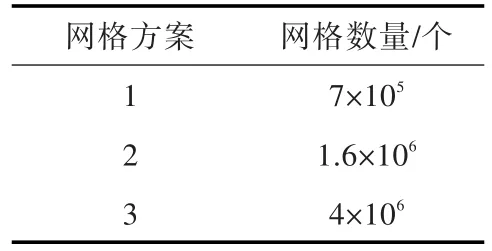
表3 螺旋桨的3套网格方案Table 3 Three mesh cases of propeller

表4 3套网格方案的推力系数和扭矩系数对比Table 4 Comparison of KTand KQof three mesh cases

由表4可以看出，3种网格方案的计算结果较为接近。鉴于计算效率和时间要求，本文将选用网格2进行后续计算。

2）直航工况。

直航工况下，吊舱推进器的推力系数和扭矩系数实验值与计算值的对比如表5所示。当进速系数J＜1时，其误差均在5%以内，吻合度较高。

3）偏转工况。

偏转工况下，选取进速系数J=0.64，计算吊舱推进器在 0°，±5°，±10°舵角下的水动力性能。选取螺旋桨在1个旋转周期内的均值作为CFD计算结果，具体如图6所示。从图中可以看出：计算结果与实验结果吻合较好，变化趋势一致，误差均在3%以内；随着吊舱偏转角β的增加，桨叶推力随之增加。相对于直航工况而言，偏转工况下螺旋桨的进速较小，且随着偏转角的增加时，进速将进一步减小，故推力扭矩将随之增加。

表5 直航工况下吊舱推进器的的推力系数和扭矩系数对比Table 5 Comparison of trust coefficient and torque coefficient of podded propulsion in straight forward

图6 不同偏转角下吊舱螺旋桨的推力系数和扭矩系数Fig 6 Thrust coefficient and torque coefficient of podded propeller of different deflection angles

4.1.2 敞水工况下的桨叶载荷分析

1）单螺旋桨斜流工况下的桨叶受力分析。

为了分析吊舱桨偏转后的压力分布情况，首先将考虑单螺旋桨偏转工况。如图7所示，以右侧斜流为例，定义正对着吊舱体支柱的桨叶为主桨叶，桨叶周向角θ=0°。桨叶向右旋转时，方向为正，周向角增加，其中叶剖面处的来流定义为

式中：Vtangential为叶剖面处来流的周向速度；Ω为螺旋桨旋转角速度；r为桨剖面半径。

在固定斜流下，轴向速度Vx不受螺旋桨周向角变化的影响，而周向速度Vtangential则受其影响，这将导致桨叶剖面在不同位置处的攻角α发生变化，其中

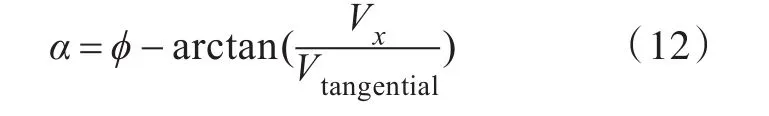
式中，ϕ为桨叶剖面的螺距角。由式（12）可知，随着螺距角的改变，攻角随之不断变化。

图7所示为不同周向角下桨叶叶剖面攻角与纯轴向流（β=0°）对比图，其中桨叶1的叶剖面攻角比纯轴向流小，对应的桨叶推力也较小；桨叶2的叶剖面攻角比纯轴向流大，对应的桨叶推力也较大。根据cos函数特征和式（11）、式（12）可知，桨叶在θ=0°时攻角和推力最小；θ=180°时攻角和推力最大。同理，对于左侧斜流而言，桨叶在θ=0时推力最大，θ=180°时推力最小。

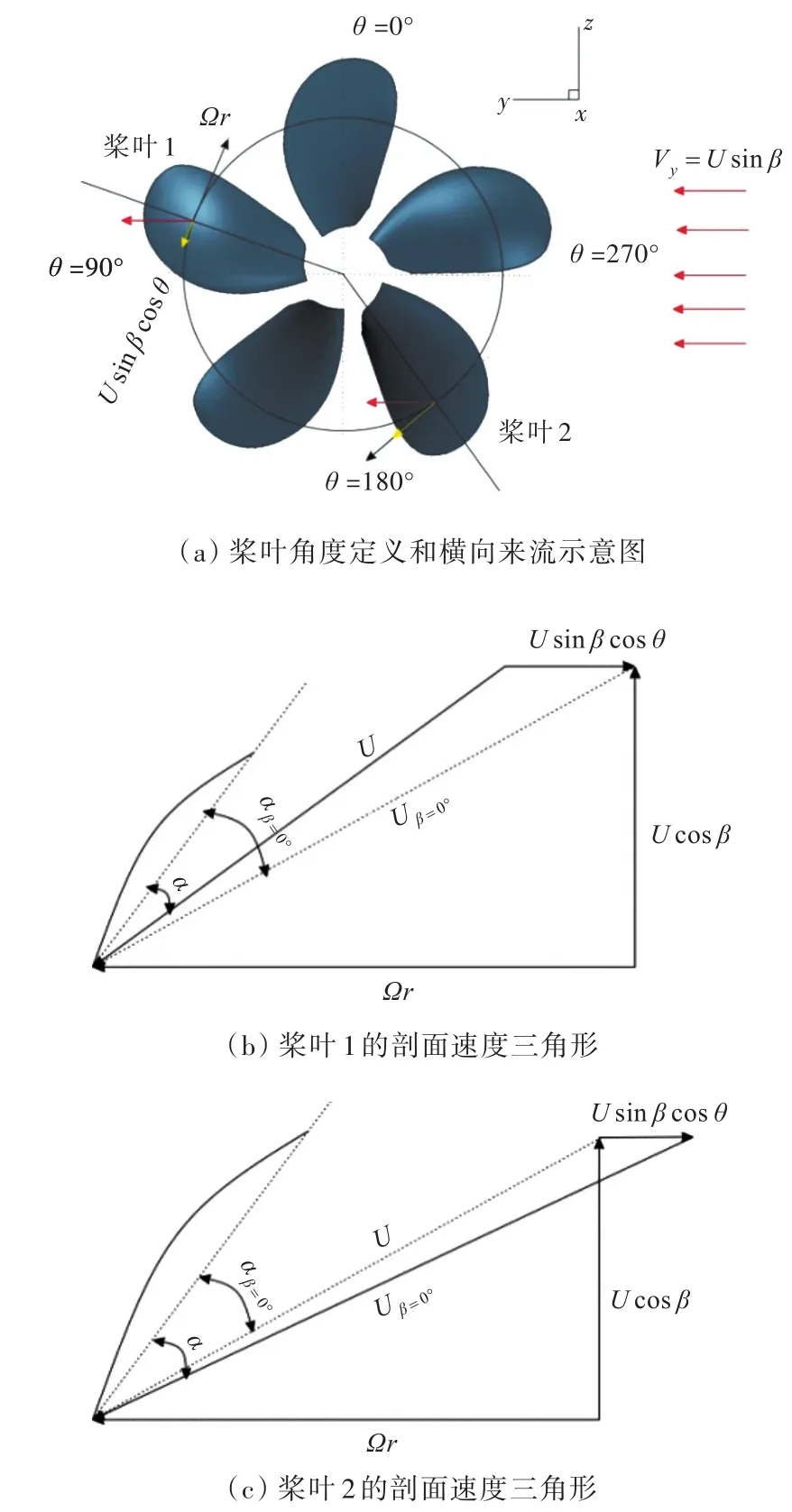
图7 桨叶剖面的水动力分析Fig.7 Hydrodynamic analysis of blade section

2）吊舱桨受力分析。

在主桨叶的1个旋转周期内，各偏转角下吊舱推进器的推力如图8所示。

图8 主桨叶一个旋转周期内的推力系数和扭矩系数曲线Fig.8 Curves of thrust and torque coefficient of the main blade in one rotation period

由图可知：

（1）在直航工况下，由于吊舱支柱的阻塞作用，吊舱推进器在θ=0°时推力最大。

（2）向右偏转时，从理论上讲，θ=0°时桨叶压力最小，但由于吊舱支柱的阻塞效应，桨叶压力最小值延迟至θ=50°左右；同理，压力最大值出现在θ=240°左右。

（3）向左偏转时，在θ=0°时桨叶压力最大，这一方面源自吊舱支柱的阻塞作用，另一方面则来自斜流的影响。由于吊舱阻塞效应对桨叶的干扰，其桨叶压力最小值延迟至θ=225°左右。图9所示的桨叶压力分布也直观反映了桨叶推力系数的脉动变化规律。

（4）随着偏转角的增加，主桨叶推力和扭矩的波峰/波谷周向位置没有发生变化，桨叶推力的脉动幅值增加，吊舱推进器的激振力也随之增加。

各偏转角下桨叶的压力分布如图9所示，其中左图为吸力面，右图为压力面。由图可知：

（1）直航工况下，支柱正前方桨叶吸力面叶梢的负压偏小；由于吊舱的阻塞作用，支柱正前方桨叶压力面的正压偏大。

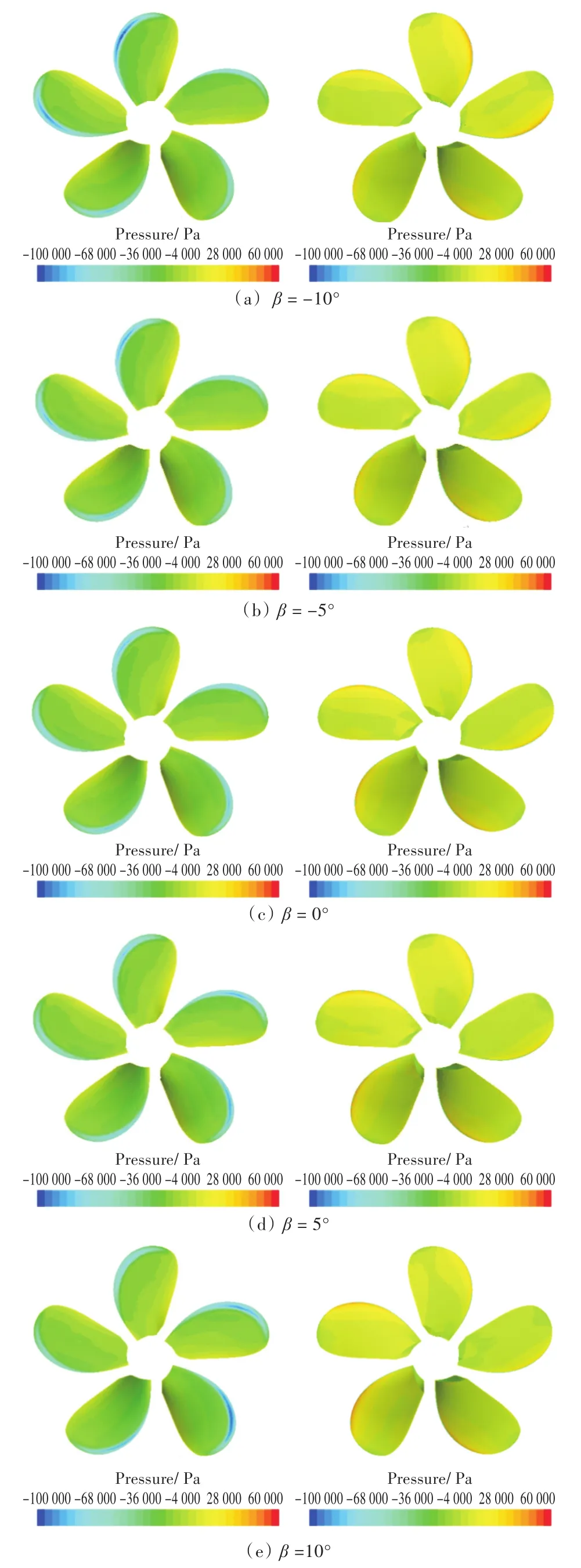
图9 桨叶压力分布云图Fig.9 Blade pressure distribution contours

（2）偏转工况下，各桨叶在不同周向位置的压力有所不同，其沿垂向和水平方向呈非对称性，这将导致吊舱桨的轴承力和激振力有所增加。随着吊舱偏转角的增加，压力的非对称性将持续恶化。

（3）桨叶向左偏转时，吸力面右侧和上侧的叶梢负压增加，压力面的正压也相应增加；向右偏转时，吸力面右侧和下侧的叶梢负压增加，这表明偏转工况会对螺旋桨的空化性能产生不利影响。

压力系数CP的计算公式为

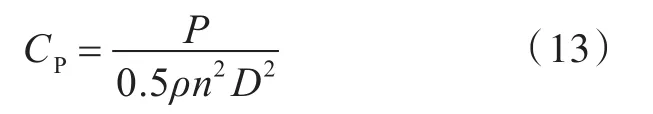
式中，P为桨叶上的压力。

图10所示为r=0.8R处的叶剖面压力系数分布曲线，可以更好地描述不同偏转角下的压力场分布，其导边开口越大，表明对应处叶剖面的攻角越大，则相应的叶面载荷就越重［13-15］。

图10（a）～图10（e）所示为各周向角（β=-10°，0°，10°）下的压力系数分布曲线。由图可知：当x/c＜0.2（c为弦长，x为弦长的某一位置）时，吸力面压力系数曲线将首先下降至最低点，然后再上升，这与桨叶本身的攻角有关，从图9也可以看出这一现象；当θ=0°，72°时，向左偏转桨叶的载荷高于向右偏转桨叶，而当θ=144°，216°，288°时，向右偏转桨叶的载荷高于向左偏转桨叶；当周向角θ=0°，216°时，各偏转工况下压力系数分布曲线的区别较为明显。

图10（f）～图10（h）所示为各偏转角（θ=0°，72°，144°，216°，288°）下的压力系数分布曲线，由图可知：在直航工况下，β=0°，θ=0°时，支柱附近的压力系数曲线开口最大，桨叶载荷较重；由向左偏转（β=-10°）的压力曲线分布可知，θ=0°时压力曲线的导边开口最大，说明此时桨叶载荷大于其他周向角，θ=216°时压力曲线的导边开口和桨叶载荷最小；由向右偏转（β=10°）的压力曲线分布可知，θ=216°时压力曲线的导边开口最大，说明此时桨叶载荷大于其他周向角，θ=72°时压力曲线的导边开口和桨叶载荷最小。

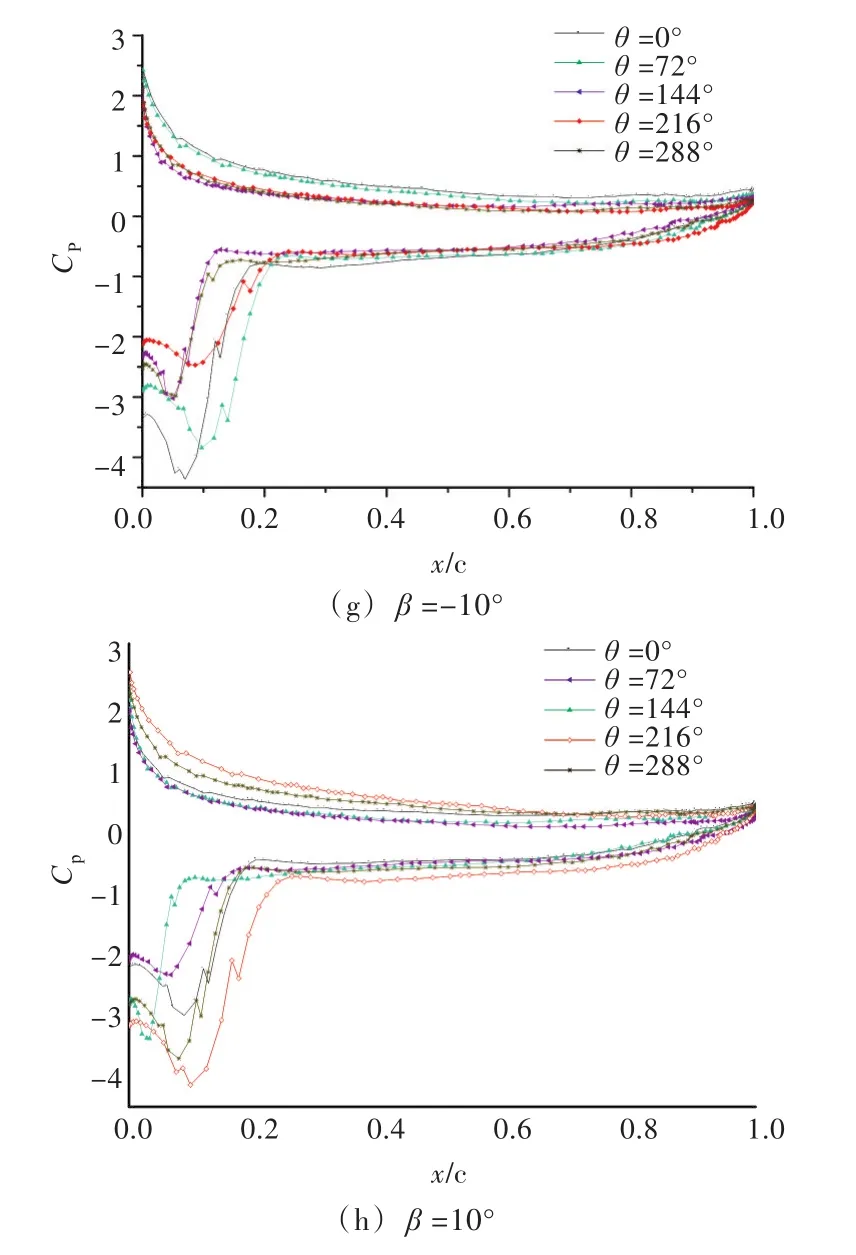
图10 r=0.8R处的压力系数分布曲线Fig.10 Blade section pressure coefficient distribution at r=0.8R

4.2 空泡性能分析

为了分析吊舱推进器在偏转工况下的桨叶空泡性能，本文开展了空泡实验和数值仿真，其结果如图11所示，其中，左图为实验效果图，中图为数值模拟图，右图为数值模拟的局部图。由图可知：

1）不同偏转角下，空泡实验与数值仿真结果的吻合度较高。

2）吊舱直航时，各桨叶的空化面积基本一致，空化比较稳定。由于支柱的阻塞作用，靠近支柱附近的桨叶空化面积略大。

3）吊舱偏转时，不同桨叶的空化面积有所不同，且这种差异性将随偏转角的增加而增加。在偏转工况下，桨叶的空化程度比直航工况严重。

4）吊舱向左舷偏转时，桨叶转至桨盘面上侧和右侧时的空泡面积明显大于其他位置；吊舱向右舷偏转时，桨叶转至桨盘面下侧和左侧时的空泡面积大于其他位置。这是因为偏转改变了来流方向，所以不同周向角下的桨叶来流大小和攻角也有所不同，而吊舱的阻塞作用将导致支柱附近的桨叶出现严重空化，从而使不同偏转方向下的桨叶空化面积存在差异。

5）斜流条件下，桨叶的空化面积随周向角的变化而变化，空泡的生成和溃灭将引起船体表面的激烈脉动，同时，剧烈的空化作用将严重剥蚀桨叶材料。

5 结 论

本文针对偏转工况下的吊舱推进器，分析了其水动力性能和空泡性能，得到如下结论：

1）结合RANS方法、Schnerr-Sauer空泡模型和全结构网格，可以精确预报吊舱推进器偏转工况下的水动力性能和空泡性能。

2）直航工况下，支柱附近桨叶的压力面正压较大，吸力面负压较大。吊舱发生偏转后，桨叶攻角和桨叶受力不断变化，但由于吊舱的阻塞作用，桨叶压力的波峰/波谷并未出现在0°或180°处，而是发生了一定的角度偏移。随着偏转角度的增加，桨叶压力脉动的波峰/波谷周向位置没有发生变化，但脉动幅值有所增加，这将对吊舱桨的激振力产生不利影响。

3）吊舱桨叶的压力分布沿周向角不断变化，其横向和垂向压力分布存在非对称性，且这种非对称性会随偏转角的增加而恶化。

4）在偏转工况下，吊舱推进器桨叶在各周向位置的空泡大小不一样。向右偏转时，左侧和下侧的空泡较大，上侧和右侧的较小；向左偏转时，右侧和上侧的空泡较大，左侧和下侧的较小。螺旋桨空泡的脉动变化将导致船体表面激烈的脉动，进而严重损坏船体和桨体材料。