脉冲性负荷柴油发电机组特性分析

吴骏，庞宇，赵凡琪

中国船舶及海洋工程设计研究院，上海200011

0 引 言

综合电力系统（IPS）是舰船电力系统的未来发展方向，它将发电、输电、变电和配电进行集成，以实现舰船推进功能，并可满足通信和导航系统等舰船负荷的用电以及合理进行能量管理及负荷自动控制的需求［1］。舰船上的电力电子设备众多，其非线性电力负荷会对电能质量造成严重影响［2-4］，尤其是高能武器、雷达等呈现的周期脉冲性瞬态特性明显。鉴于其特殊的能量需求和运行特性，在给系统的稳定运行带来新的挑战的同时，也给舰船电力系统的发展带来了机遇。

国内许多大学和研究所已经针对脉冲性负荷柴油发电机组开展了研究。例如，在脉冲性负荷大幅度波动而又需要保证有较高供电质量的应用中，研究改善机组调速率，优化供电频率和电压，并减少波动负荷对系统造成的不良影响。袁利国和邢广笑等［5-6］对影响机组性能的柴油机功率的确定、储能飞轮设计、调速系统性能匹配以及增压器匹配设计等因素进行了研究。赵同宾等［7］通过建立的脉冲性负荷柴油发电机组仿真模型，分析了机组宏观性能参数的动态特性，并从微观上描述了柴油机动态热力过程。李天水等［8］通过理论分析模型和虚拟样机模型，分别对机组轴系在柴油机的输出扭矩和脉冲扭矩下的动态特性进行了分析，为机组优化设计奠定了基础。

对于脉冲性负荷的供电，目前大多数文献主要研究了机械储能和电容储能这2种技术途径。本文在2艘含大功率脉冲性负荷的实船电力系统设计过程中，发现雷达的种类和功率不同，其运行特性、影响及其解决方法也会有很大差异。

本文将根据功率特性将脉冲性负荷雷达分为2类，以便采取不同种类负荷的解决方法。重点研究第1种平均功率变化不大的等效恒稳负荷，提出采用柴油发电机组固有的机械储能来平抑功率波动，并对柴油发电机组转轴的动态特性进行研究，以分析在负荷波动下机组调速器介入的前、后阶段和稳态阶段的转速变化率，为实际工程应用中机组的选择和配置提供理论依据。

1 测量船发电机组雷达负载特性分析

1.1 脉冲性负荷运行特性

大型电力电子设备和电动机械装置的迅猛发展促使了脉冲能量及新型储能装置的研发。脉冲能量的需求在数十千焦到几千兆焦之间，瞬时功率基本都在兆瓦级以上，而未来舰船可能的脉冲负荷种类很多，例如激光武器、电磁弹射、大功率雷达等。本文所研究的脉冲性负荷为雷达。

由于以往雷达电源大多采用陆上电网，容量很大，雷达功率一般在1 MW以下，故由电网直接承受脉冲功率。传统上，在含雷达的舰船电力系统中，雷达功率与发电机功率相比都较小，脉冲性负荷的影响不是特别明显。尽管在舰船电力系统中使用兆瓦级以上大型雷达的案例不多，但也出现过影响发电机频率导致发电机组无法并网的情况［9-10］。

雷达负荷是一种高频脉冲性负荷，根据功率波动的外特性分为2种情况：一种是在负荷不同的工作模式下，平均功率变化不大的等效恒稳负荷；另一种是由于工作性能特殊，负荷功率波动的周期和占空比都不确定且平均功率变化很大，不能等效为恒稳的负荷，如图1所示。不同外特性的雷达负荷，其系统解决方法不同，这是因为柴油发电机的转轴具有转动惯量，会对电磁功率的波动起到阻尼作用，故工程应用中多利用柴油发电机固有的机械储能来平抑第1种负荷的功率波动。本文研究的是第1种负荷。第2种负荷需电容储能来解决，未来将进一步开展研究。

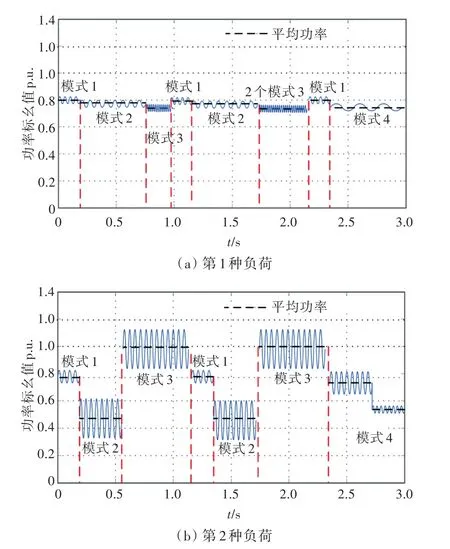
图1 不同雷达负荷的功率特性对比Fig.1 Power characteristics comparison of different radar loads

表1所示为雷达的典型工作模式。当雷达T/R组件工作在大脉宽（脉冲宽度）、小工作比时，将导致雷达系统输入的供电功率出现高频功率波动，严重影响发电机组的正常工作，故雷达在运行时会避免使用大脉宽、小工作比模式。需要说明的是，为减小负荷对系统的影响，其供电装置中已包含了滤波单元和储能电容。图2所示为雷达中某模块在典型工作模式下的功率波动情况，图中，PRT为脉冲重复周期。

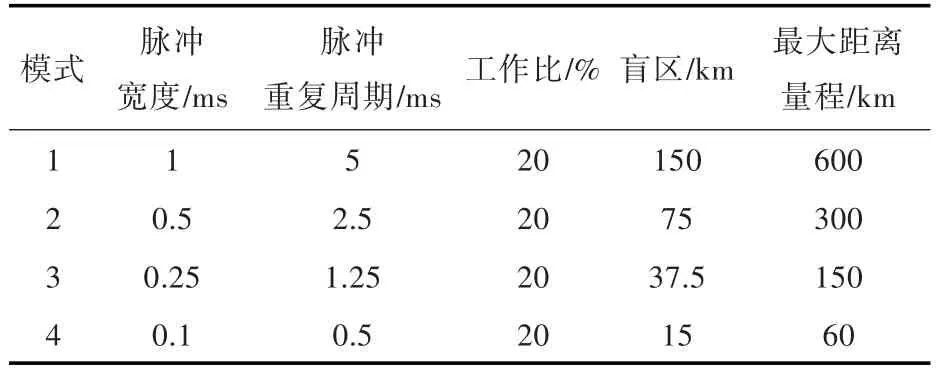
表1 雷达某模块典型工作模式Table 1 Typical operation modes of a radar unit

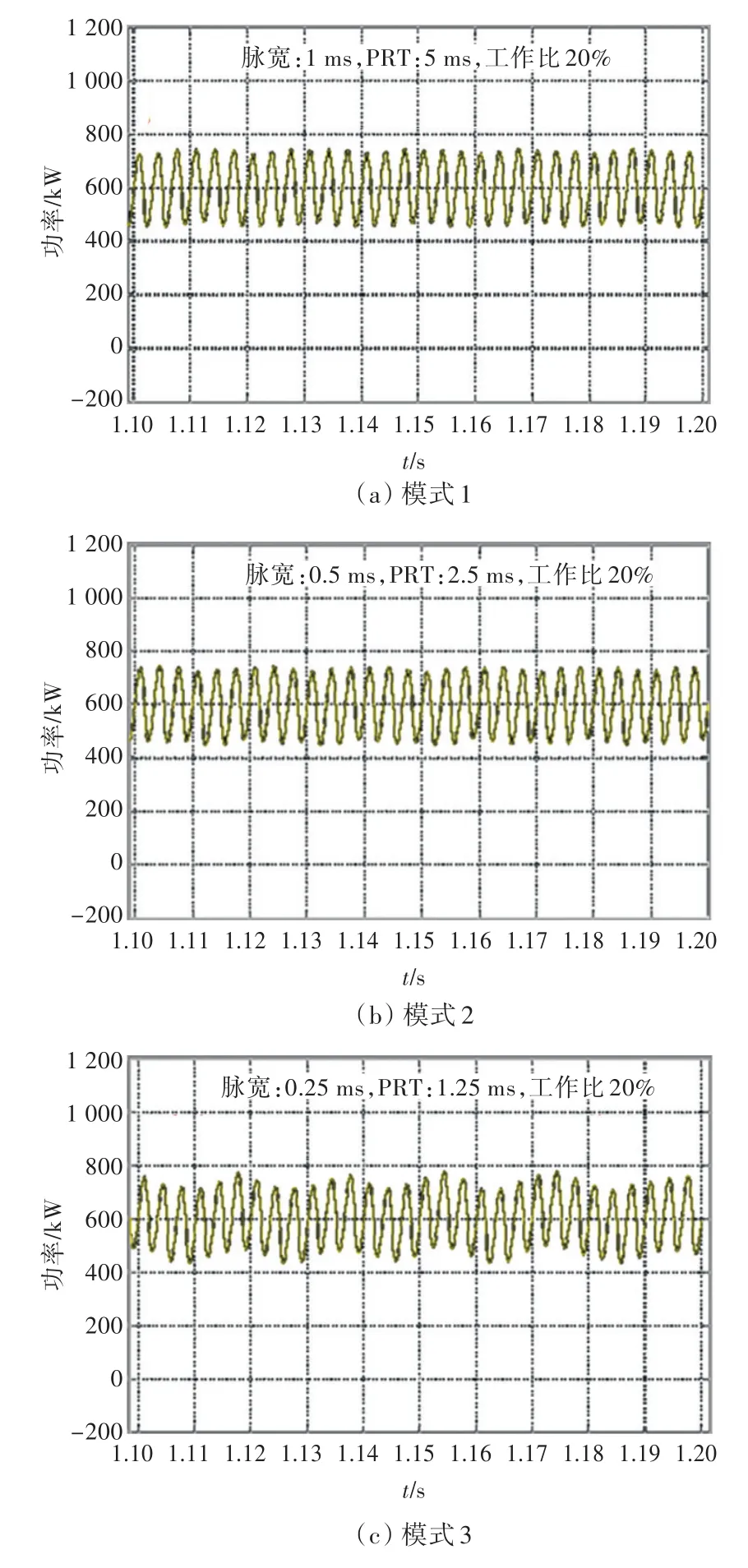
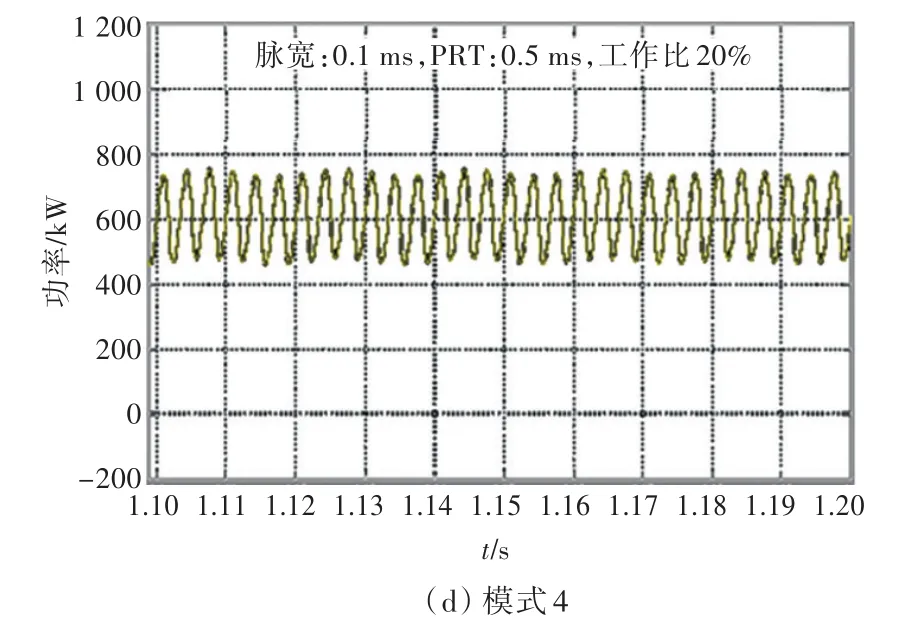
图2 4种工作模式下雷达功率波动Fig.2 Power fluctuations of radar in four operation modes

雷达系统中既包含高频舱、水冷等稳定用电负荷，也包含有造成功率波动的雷达阵面负荷（以下称“阵面负荷”）。由图2可看出，该类雷达功率波动的外特性为一个周期内的功率在稳定值附近波动，故可视为稳恒负荷。

文献［11］认为脉冲性负荷柴油发电机组的工作特性是：负载在空载和带载间周期性波动，机组大部分时间运行在动态过程中，载荷幅度有时甚至超过机组额定负荷。实际上，脉冲性负荷机组的负载范围不只是在“空载”和“带载”之间波动，也可能是在低负荷和高负荷状态下波动。低负荷可能是空载、较低负载，甚至还会出现机组负载倒拖；高负荷可能是机组额定负荷内的较高负载，也可能远远高于额定负荷，如短时持续高负荷。

本文为了研究雷达供电柴油发电机组的调速、发电机调压性能能否解决负载功率变化的问题，重点考虑了2种工况。

1）突加严重工况（工况1）。

即在1.2 MW稳定负荷下，突加4.25 MW负荷，同时有±0.2 MW的负荷波动，波动周期为15 ms。负荷总用电为5.45 MW，波动范围为5.25～5.65 MW，如图3所示。

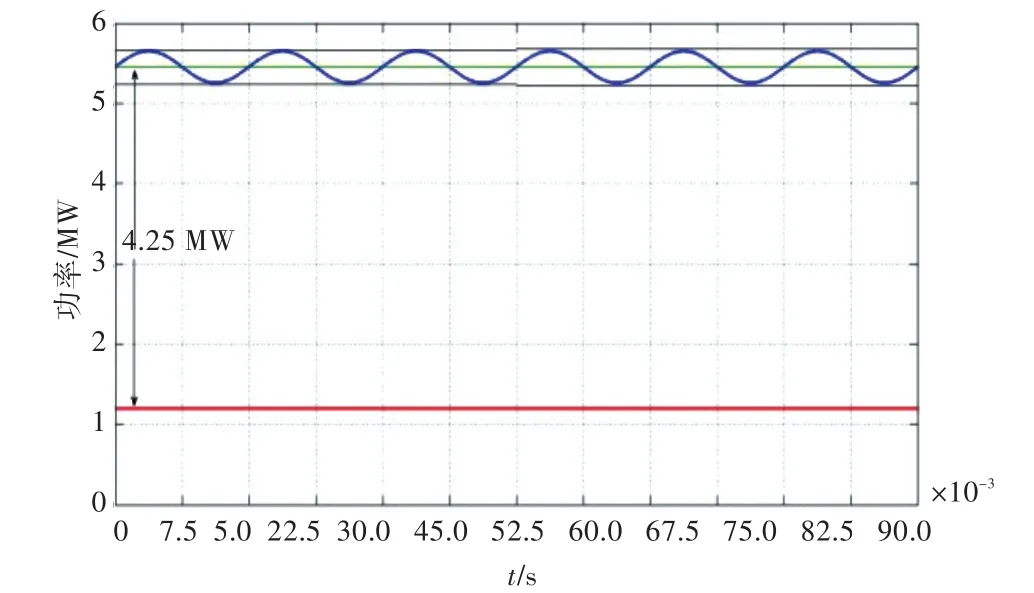
图3 工况1的雷达阵面负荷Fig.3 Front loading of radar in operation mode 1

2）波动最严重工况（工况2）。

即在1.17 MW稳定负荷下，突加2.43 MW负荷，同时有±1.875 MW的负荷波动，波动周期为33 ms。负荷总用电为3.6 MW，波动范围为1.72～5.47 MW，如图4所示。

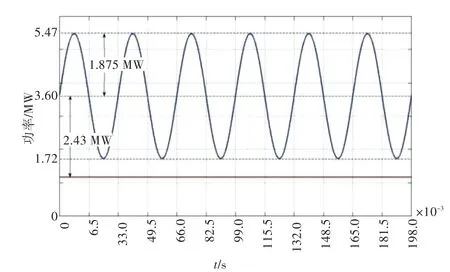
图4 工况2的雷达阵面负荷Fig.4 Fiont loading of radar in operation mode 2

1.2 系统组成

电站配置6台5.8 MVA（1 000 kW）发电机组，雷达电源与6.6 kV交流电网连接。在雷达工况下，3台机组为雷达提供电能（即脉冲性负荷柴油发电机），1台机组供给日用负荷，1台机组供给推进负荷，如图5所示。雷达阵面最大能耗为5 MW，由5个电源模块供电，阵面由直流供电，电压额定值为520 V，直流电压波动范围为+6%～-10%。

2 柴油发电机组动态特性理论分析

以转轴为分析对象，理论推导不同负荷下的转轴角速度波动情况。

2.1 转矩方程与转轴角速度变化的关系

根据转矩方程，机组转轴上的转矩T之和以及转轴转动惯量J构成了角速度ω的变化，如式（1）所示［12］。

旋转运动中的功率P定义为转矩和角速度的积，如式（2）所示。

联立式（1）及式（2）可得到转轴上的功率之和及角速度变化的关系式，如式（3）所示。

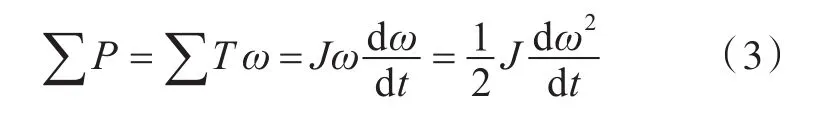
其中，转轴上的功率之和为原动机提供的机械功率PT及发电机转换的电磁功率PE，如式（4）所示。

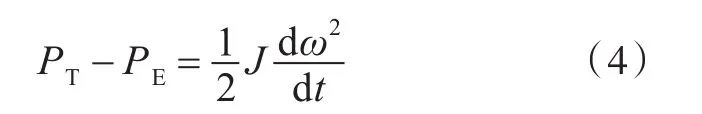
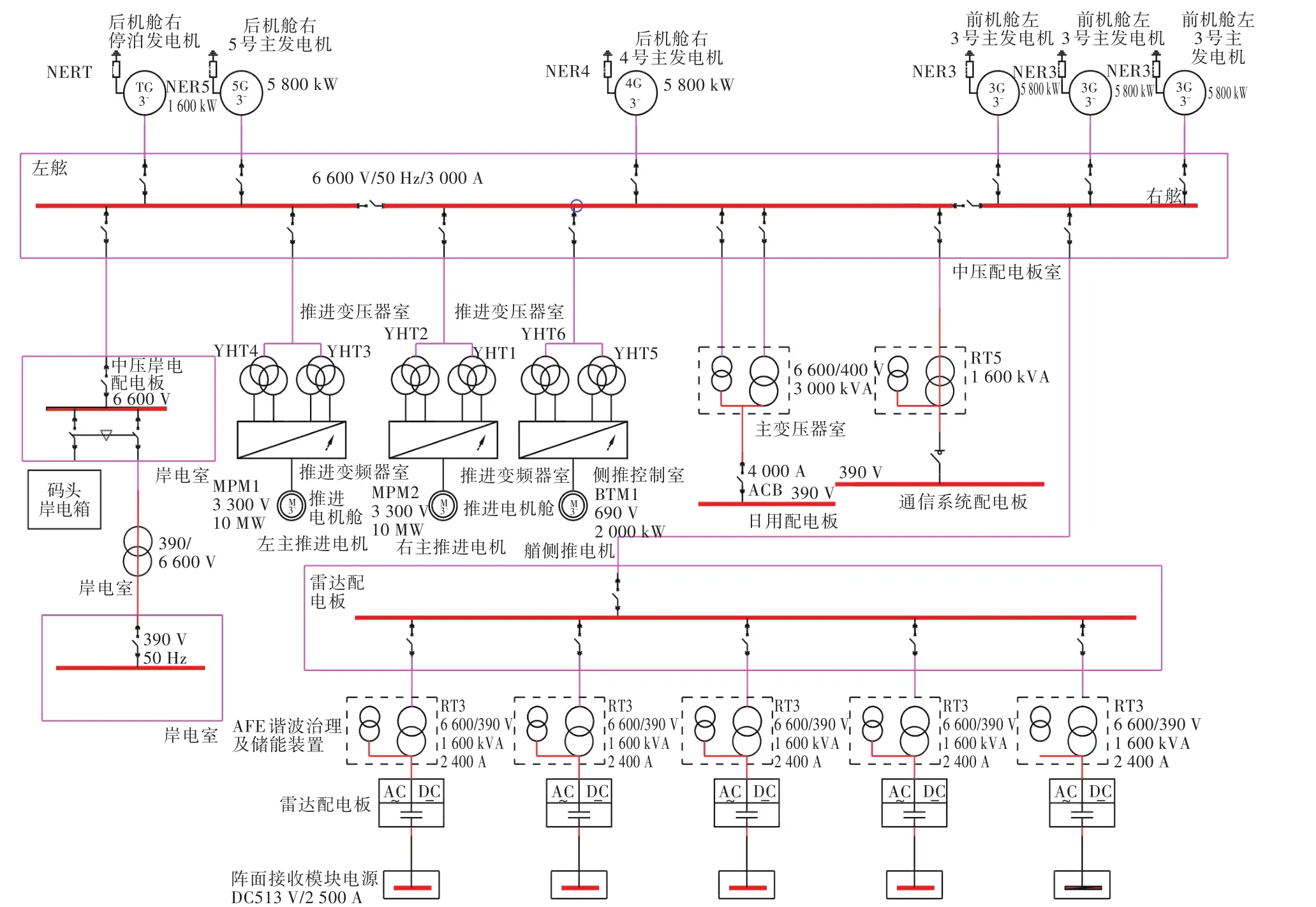
图5 测量船电力系统示意图Fig.5 Schematic diagram of power system for a survey ship

在稳定状态下，机械功率与电磁功率相抵，使转速保持稳定，即

暂态时，两者此消彼长构成了角速度变化，如式（6）所示。

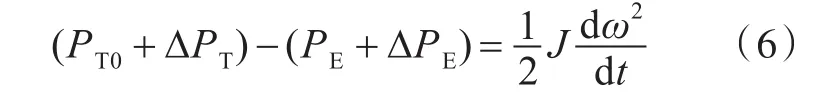
联立式（5）和式（6）可知，自稳定状态变化、机械功率增量ΔPT及电磁功率增量ΔPE共同构成了角速度变化，如式（7）所示。

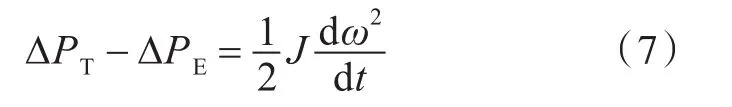
鉴于电磁功率的变化被认为是瞬时的，而原动机输出的机械功率变化存在响应时间（t），在机组调速器来不及响应而供油量暂时不变时，ΔPT=0。阵面负荷所需电磁功率变化如图6所示。图中，A为波动功率，B为突加功率，Tp为波动周期。

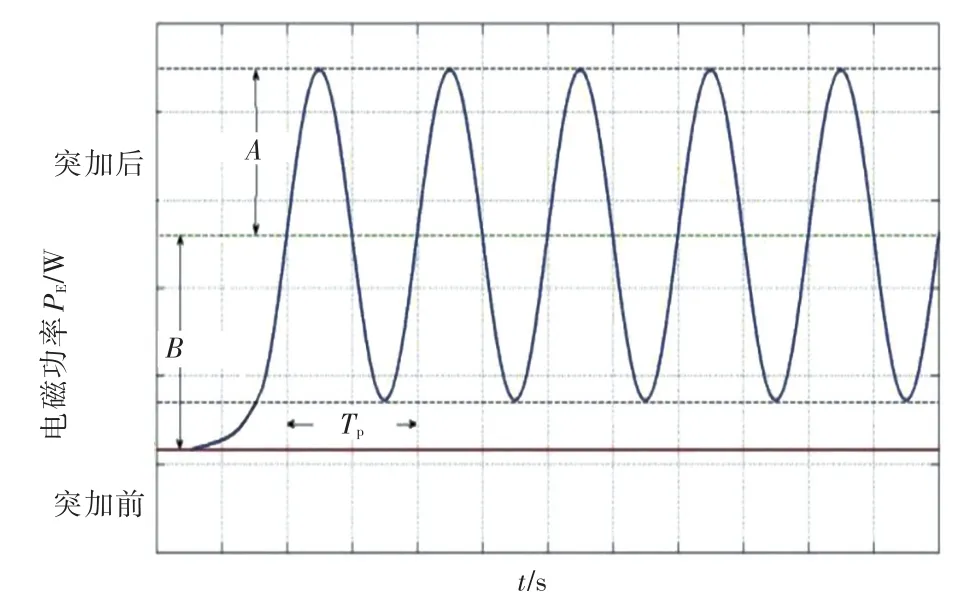
图6 雷达阵面负荷突加Fig.6 Sudden increase of front loading in radar

根据图6，阵面负荷所消耗的电磁功率可用式（8）表示，其中ωp为波动频率。

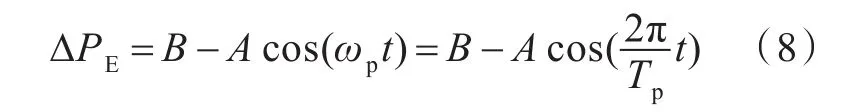
将机械功率增量（ΔPT=0）及电磁功率增量代入转矩方程式（7），可得原动机调速执行机构变更油量前的角速度波动表达式如下：

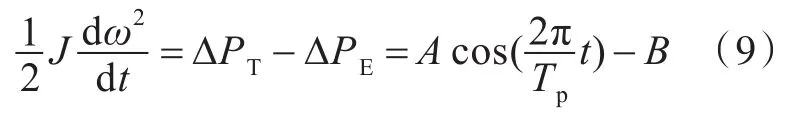
整理后，得到关于角速度的微分方程如下：

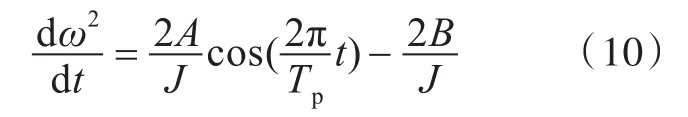
对式（10）积分一次可得

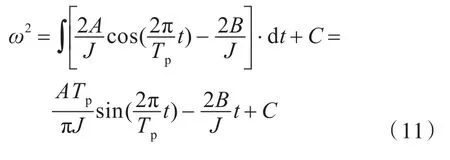
代入初始稳态时的角速度ω0，可得积分常数C，其中原动机调速执行机构变更油量前角速度的解析表达式如式（12）所示，该式可用于油门调整前角速度变化的定量计算。

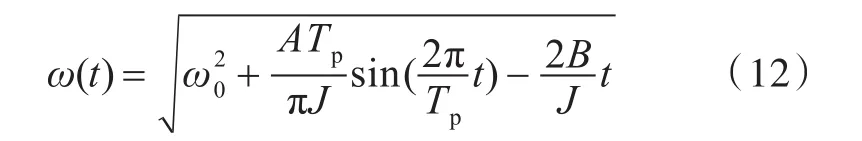
2.2 机组3个过程中转速变化情况

2.2.1 调速执行机构介入前的转速跌落

初始状态时，调速机构尚未介入工作，故此时消耗的转轴动能转化为电磁功率，转轴处于纯减速状态。继续按式（12）计算，该式持续时间取决于油门的响应速度及调速器的控制时间。经延时后，调速机构介入工作，变更油门供油，转入下一个阶段。

式（12）中有关机组的参数均有典型值，而关于阵面负荷的参数又已知，故可进行初步的理论计算。通过调整机组转动惯量及额定转速n，可以改变调速执行机构介入前的转速跌落特性，如图7所示。由图可知，单台机组转动惯量越大，或并联机组数量越多，亦或增加机组的额定转速，可减缓转速下降，使暂态特性变好。

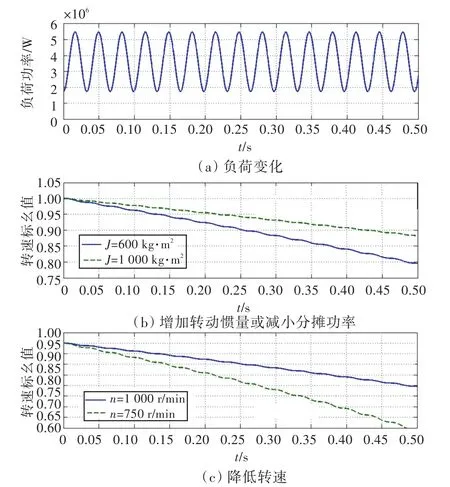
图7 调速执行机构介入前的转速跌落Fig.7 Speed drop without the speed control mechanism

由图7还可知，增加的波动分量对突加负荷不会产生重大影响，仅在原始突加波形上增加了抖动，但总体趋势未变，不会影响调速器的作用，所以突加阵面负荷的特性可近似为突加。

2.2.2 调速执行机构介入后的过渡过程

过渡态时，调速机构介入工作，油门供油量改变，增加G（t）项，以表示调速器执行机构自变更油门开始产生的机械能累计量，则式（12）可修正为在整个调速过程中的普适表达式（13）。但因G（t）项不能用解析式表示，故式（13）仅可用于定性分析。

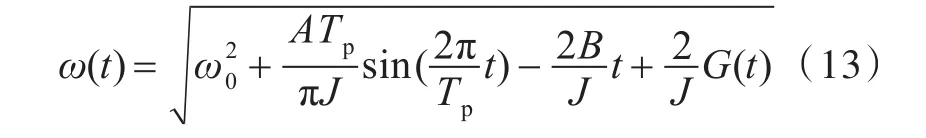
式中：根式内第1项为初始角速度；第2项为阵列产生的功率波动导致的机械能变化量；第3项为阵列突加功率产生的机械能缺口；第4项G（t）为执行机构增加供油量补充的机械能，执行机构反应前G（t）=0时，式（13）简化为式（12）。

需要说明的是，将式（13）中的根式打开后，等式左右两侧均乘以J2，则该式在物理意义上与能量守恒定律等价。

在开始加油门后，当G（t）＞0时，机组额定转速跌落开始缓解；当G(t)＞B·t后，新增机械能超过突加电磁功率，转速开始止降回升。在此过程中，转速变化量会对转速检测产生影响，但总体趋势不变。

2.2.3 稳态后的转速波动

在稳态时，油门恒定，新增油量产生的功率与稳态增量相抵，式（12）中的第3项、第4项消失，第2项功率波动项使角速度发生周期变化，式（12）变为

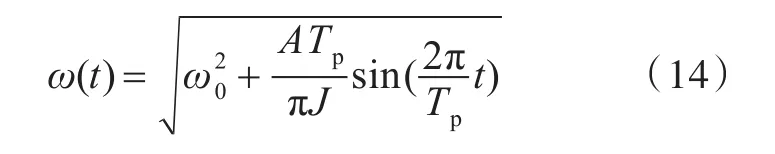
此时，最大角速度ωmax为

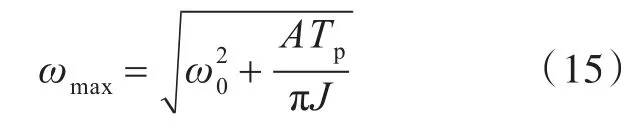
而最小角速度ωmin为

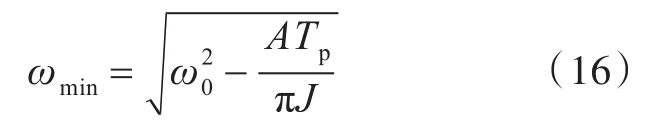
对式（14）稍作化简，将角速度按泰勒级数在t=0处一阶展开，可得

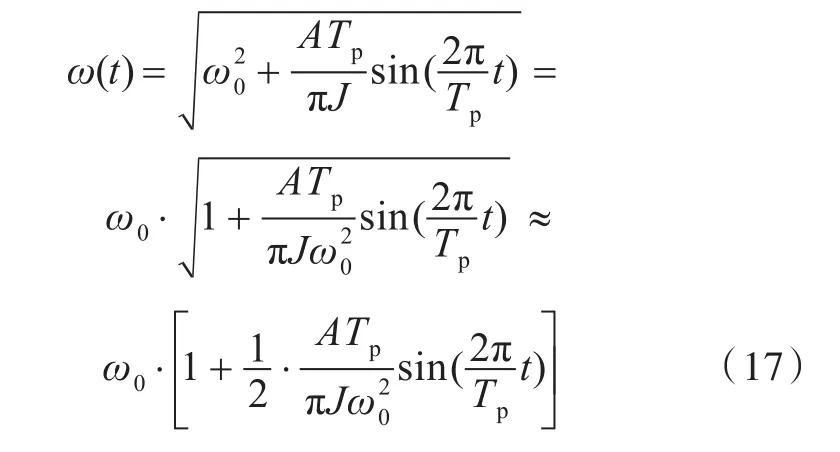
由上式可求得角速度变化率δ的上界，如下式：

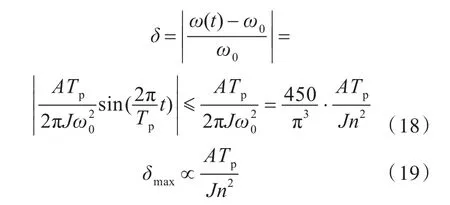
由式（19），可知角速度变化率δ的上界δmax与波动功率A和波动周期Tp成正比，与转动惯量J和机组额定转速n的平方成反比。即J越大，角速度变化率δ越小；A越大，角速度变化率δ越大；Tp越小，角速度变化率δ越小；机组额定转速n越大，角速度变化率δ越小。但一般高速机的J较小，故两者相互矛盾，应综合计算具体机型的Jn2，以对比性能。

3 工况分析及其仿真

在柴油发电机组动态特性理论分析的基础上，对1.1节中提到的2种工况进行具体计算分析。使用Matlab软件作为仿真平台，发电机采用Simulink软件自带的三阶同步发电机模型，利用经典的Woodward调速模型以及IEEE AC type1型励磁控制器模型进行船舶电站仿真研究。脉冲性负荷的输入是利用三相全桥不控整流将交流变换为直流，以受控电流源为核心元件，使其输出电流受脉冲性负荷的输出功率及电压控制。此外，利用同型机组的陆上联调实测数据，对励磁调压器、调速器进行参数辨识，使仿真模型的三级加载外特性与实验的一致。

3.1 工况1——突加最严重工况

工况1的机组型号为10L32/44CR，其他参数输入如表2时所示。

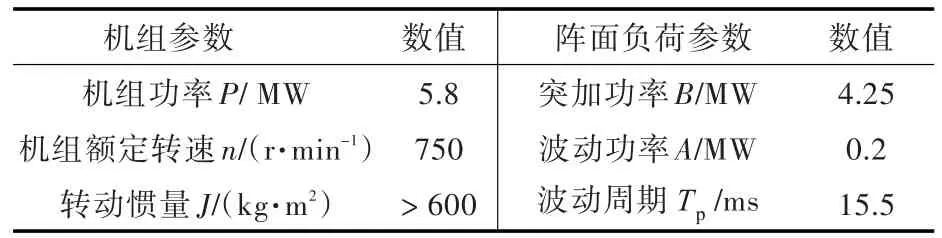
表2 工况1有关参数输入Table 2 Parameters of working condition 1

由第2节的分析可知，投入雷达阵面负荷可近似为突加负荷，波动对此基本无明显影响。原动机设备厂家提供的输入如图8所示。根据图8可计算突加负荷的转速跌落，如表3所示。其中，方案1，2和3的系统配置分别指1台5.8 MW、2台5.8 MW及3台5.8 MW。

根据第2节的分析，求解稳态时单机转速变化率。根据式（14）和式（18）可计算单机时的转速变化率，10L32/44CR机组的额定转速n=750 r/min，合计78.5 rad/s。

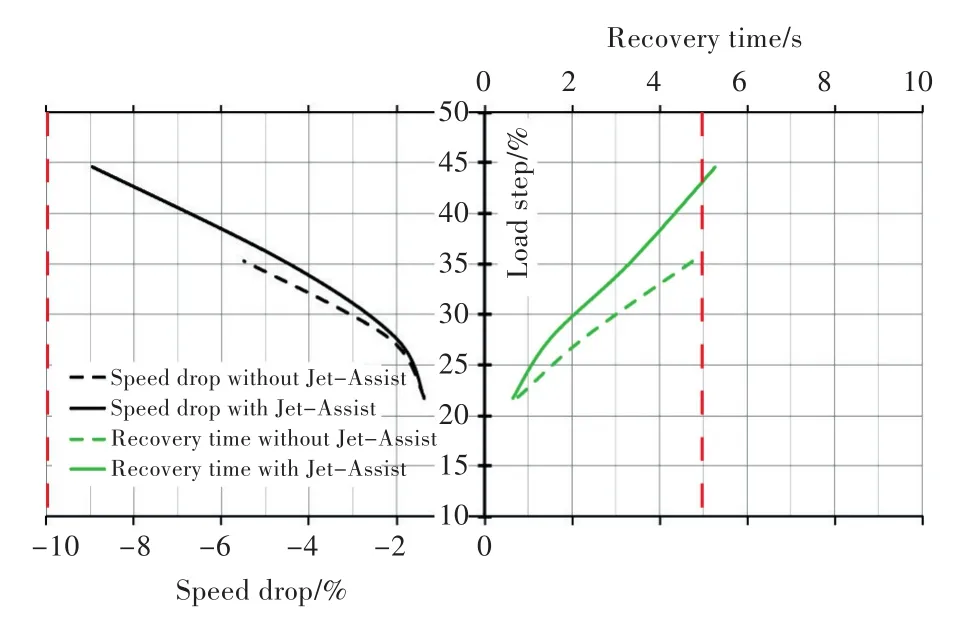
图8 10L32/44CR机组调速特性Fig.8 Speed regulation characteristics of 10L32/44CR diesel engine

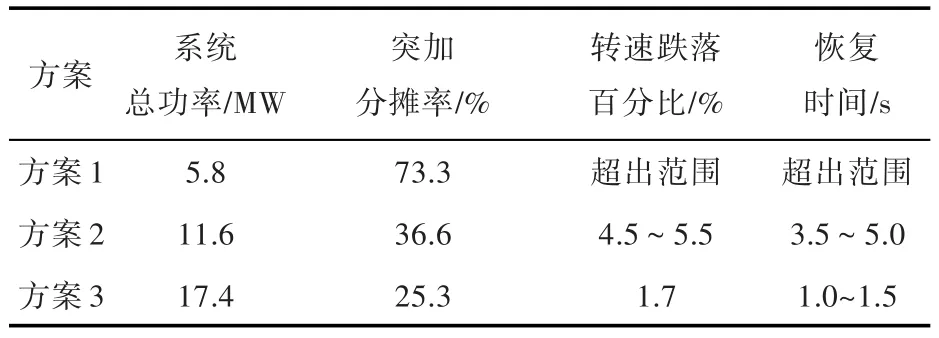
表3 不同机组配置方案突加4.25 MW功率时的转速变化Table 3 Speed changes of different unit configurations at sudden load of 4.25 MW

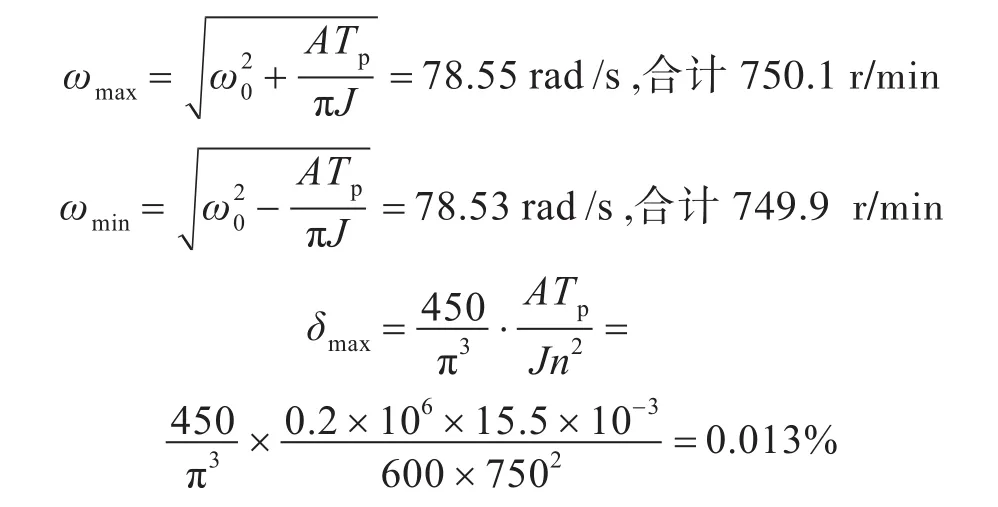
对于多台机的情况，2台机的波动功率A减小一半，3台机的波动功率A减小到1/3。根据理论计算结果，2台柴油机以上带雷达阵面负荷的工况1可满足突加时的转速特性，变化率可忽略不计。

对工况1进行仿真复核，结果如图9所示，此时各机转速跌落约5%，与计算分析数值相近，电压瞬时波动率约5%。

3.2 工况2——波动最严重工况

工况2时的其他参数输入如表4所示。根据图8可计算突加负载时的转速跌落，如表5所示。

根据第2节的分析，求解稳态时单机转速变化率。根据式（14）和式（18）可计算单机组时的转速变化率计算，10L32/44CR机组的额定转速组n=750 r/min，合计 78.5 rad/s。

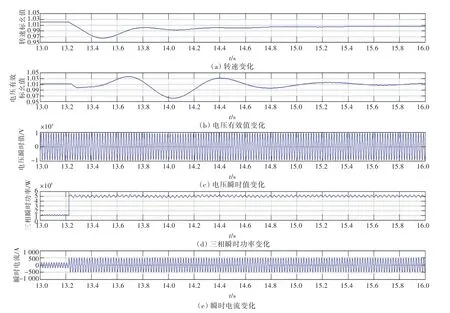
图9 工况1下2台机投入负荷波动时电力系统流动情况Fig.9 Fluctuations of two power systems in working condition 1 of two generators

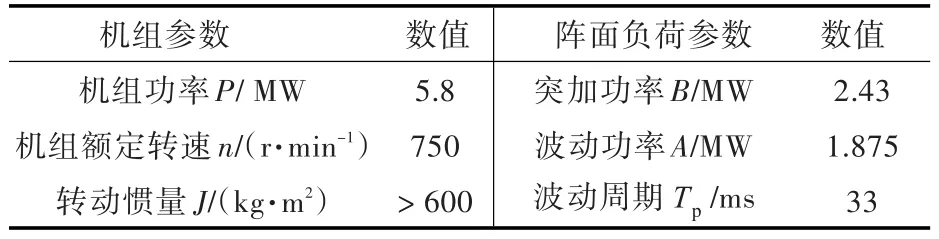
表4 工况2有关参数输入Table 4 Parameters of working condition 2

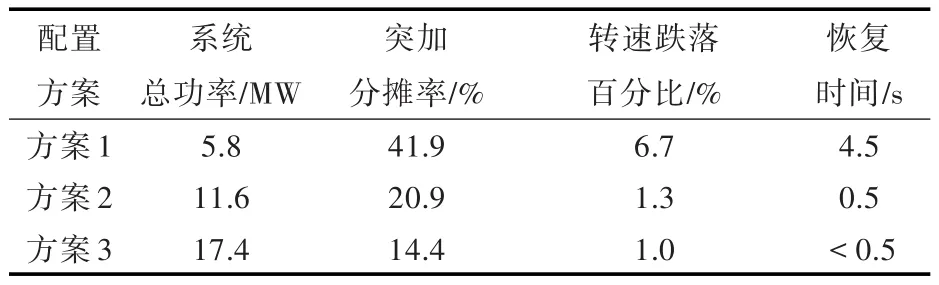
表5 不同机组配置方案2.43 MW突加功率时的转速变化Table 5 Speed changes of different unit configurations at sudden load of 2.43 MW

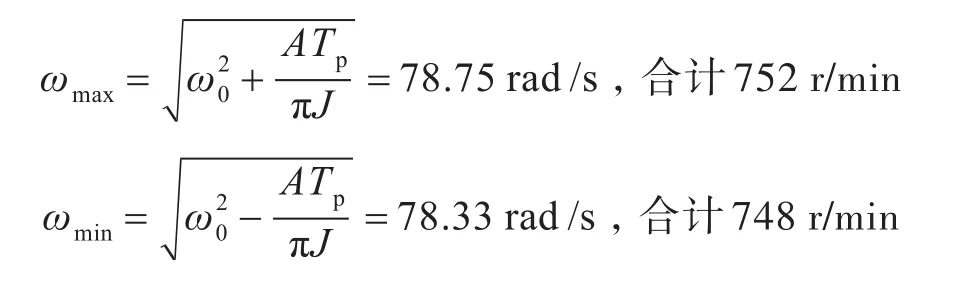
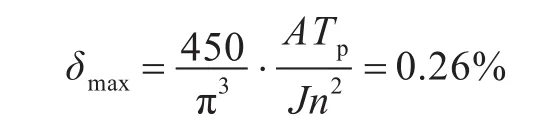
对于多台机的情况，2台机的波动功率A减小一半，3台机的波动功率A减小到1/3。该工况由于波动功率较大，在理论计算的基础上进行了基于Simulink的建模仿真复核，如图10所示。仿真计算结果的角速度变化率为0.29%，与理论计算值基本相近。

图10（e）所示的瞬时电流幅值波动的包络线即图10（d）所示的的波动功率。在此情况下，系统电流会产生较大的分数次谐波，谐波源波动负荷流通路径为自波动负荷流向供电机组，因此需要注意分数次谐波对其他设备（尤其是继电保护装置）的影响。

总之，此时1台柴油机带雷达阵面负荷的工况2可满足突加功率时的转速特性，转速变化率的理论计算值及仿真值也在允许范围内。由仿真结果还可知，系统电压特性也满足指标要求。

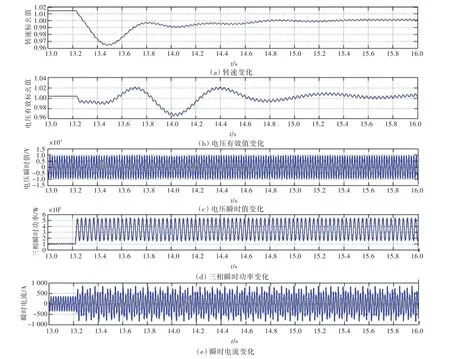
图10 工况2单机组投入负荷波动时电力系统波动的情况Fig.10 Fluctuations of single power system in working condition 2 of two generators

4 结 论

本文根据功率特性将脉冲性负荷雷达分为2类，指出不同种类负荷的解决方法不同。重点研究了第1种负荷，即在不同的工作模式下负荷平均功率变化不大且可等效为恒稳负荷的情况，提出采用柴油发电机组固有的机械储能来平抑功率波动。以测量船为例，对为其大功率雷达供电的柴油发电机组转轴动态特性进行了分析研究，理论推导出了调速器介入前、后的转速跌落、恢复规律和稳态过程中的转速变化率。对2种典型工况进行了仿真计算，并与理论结算结果进行比较，得到如下结论：

1）在突加最严重工况下，对于2台柴油机以上带雷达阵面的负荷，在该工况下可满足突加负荷时的功率转速特性，变化率可忽略不计；

2）在波动最严重工况下，对于1台柴油机带雷达阵面的负荷，在该工况下可满足突加负荷时的转速特性，转速变化率在允许范围内，同时系统电压特性也满足指标要求。

在理论分析的基础上，本文针对测量船雷达实际工况的负荷特点，计算得到所配置柴油发电机组的容量及其性能指标，并通过仿真验证了理论推导的正确性。研究结果可为用柴油发电机组固有的机械储能来平抑此类型脉冲性负荷功率波动提供量化标准，并形成系统、理论的工程总结。