大型柔性阵面阵架动力学分析*

刘 广，俞刘建，冯康军，许 泉，张晓宏

（上海机电工程研究所，上海 201109）

引 言

阵面阵架是专门设计的结构框架，其功能是安装、支撑辐射天线阵列，形成辐射场，并为辐射天线阵列的维护及射频馈电系统设备的放置提供平台场地，同时为工作人员提供系统安装、集成、调试和维护的工作平台和空间。由于曲率半径和表面积的需求，阵面阵架的尺寸和质量往往较大，其质量达数百吨级。为了保证安全性和其他性能指标，阵面阵架的结构设计要求空间利用率高、质轻且刚度高，即在充分利用既有空间，使得阵面曲率半径和表面积最大化的同时确保阵面阵架整体质量轻且刚度高。因此在阵面阵架结构设计阶段，必须对其进行必要的刚强度分析与校核，而有限元仿真和多体动力学分析是验证结构设计是否满足刚强度要求的重要手段。目前有限元仿真[1-4]与多体动力学分析技术[5-6]在雷达阵面阵架的结构设计中已经得到了广泛应用。

某大尺寸阵面阵架高8.5 m，半径为17.5 m，阵面阵架上安装了用于模拟目标及干扰源水平或垂直运动、产生宽带和大功率射频信号的机械阵。通过外部网络提供目标和干扰源的位置信息，实时传输给机械阵控制单元，然后由运动机构实现目标和干扰源的空间位置精确定位和实时运动模拟。为了确保该大型阵面阵架质量轻、刚度高，需对其进行有限元分析以评估刚度特性，并对机械阵上滑车的水平、垂直运动过程进行多体动力学分析以评估其工作时的动态性能，为阵面阵架的结构设计提供理论支撑。

1 阵面阵架结构组成

阵面阵架主要由加强架、阵面阵架和机械阵组成，其拓扑结构如图1所示。阵面阵架沿暗室对角线放置，实现了阵面阵架曲率半径的最大化，解决了现有倒扣或侧立碗式阵面阵架曲率半径相对较小、空间利用率低的问题。通过对加强架进行优化设计，该阵面阵架的质量仅为同规格钢制阵面阵架的三分之一，生产成本显著降低。机械阵安装在微波暗室的阵面阵架上，由水平导轨、垂直导轨、水平滑车、垂直滑车、控制单元（含软件）、安装架等组成。机械阵为“⊥”形结构，包括水平和垂直各一条导轨，每根导轨上安装一个滑车，滑车上搭载一个辐射天线单元安装座，在控制单元的控制下，实现水平及垂直机械运动。

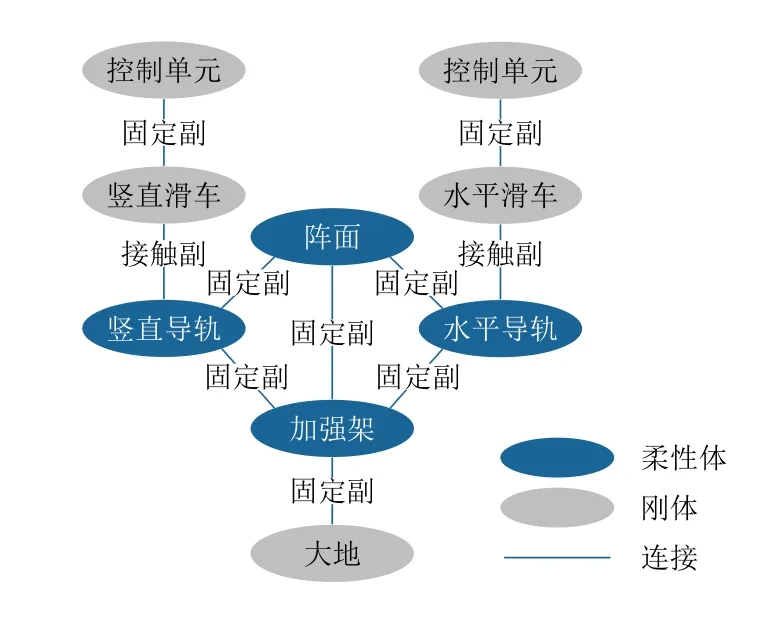
图1 阵面阵架拓扑结构图

2 阵面阵架模态分析

2.1 有限元建模

在有限元建模过程中，加强架和阵架简化为梁单元，阵面简化为壳单元，并赋予梁单元一定的截面尺寸和截面方向，赋予壳单元相应的厚度；机械阵采用六面体实体单元建模并赋予一定的材料属性。加强架各梁之间、加强架与阵架之间、阵架与阵面之间采用焊接连接方式，在有限元建模过程中采用共节点方式进行简化处理；机械阵与阵面阵架之间采用多个多点约束（Multi-Point Constraints, MPC）连接，解决体单元与壳单元自由度不协调的问题。建好的阵面阵架有限元模型如图2所示。

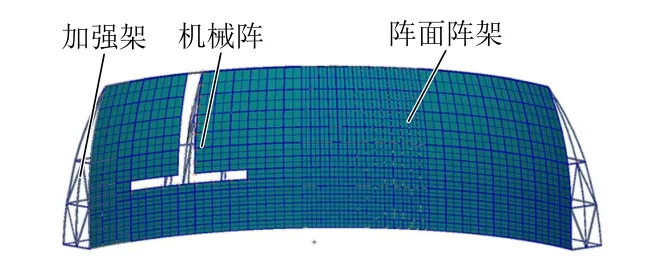
图2 大型柔性阵面阵架有限元模型

2.2 模态分析

2.2.1 模态分析理论

对建好的阵面阵架有限元模型，自由模态分析求解的基本方程为：

求解式（3）即得阵面阵架结构系统的固有频率和振型。有限元软件中求解上述方程的常见方法有跟踪法、变换法和兰索士（Lanczos）法，本文采用兰索士法。兰索士法是一种正交变换法，它通过递推算法将广义特征方程变换为标准特征方程，同时完成矩阵对角化和降阶，并且结合移频技术，适应刚度矩阵和质量矩阵奇异的情况，抽取中间任何阶特征值。因此，兰索士法是求解大型矩阵特征值问题最有效的方法。

2.2.2 模态分析结果

对建好的有限元模型进行模态分析，分析结果如表1和图3所示。

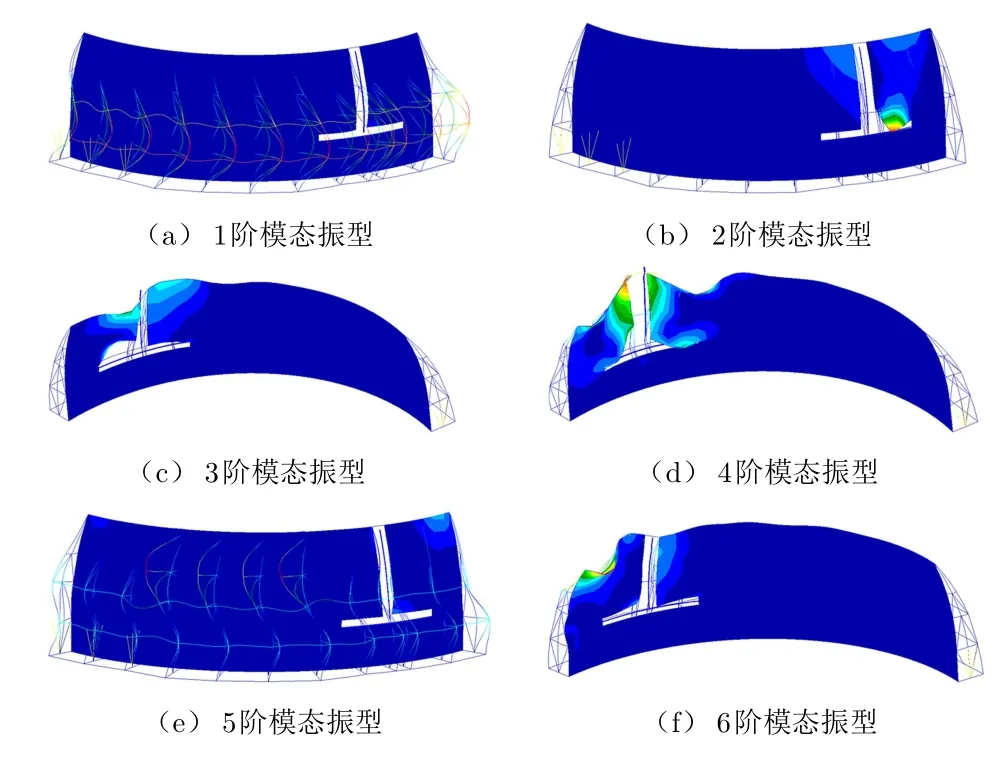
图3 阵面阵架前6阶振型图

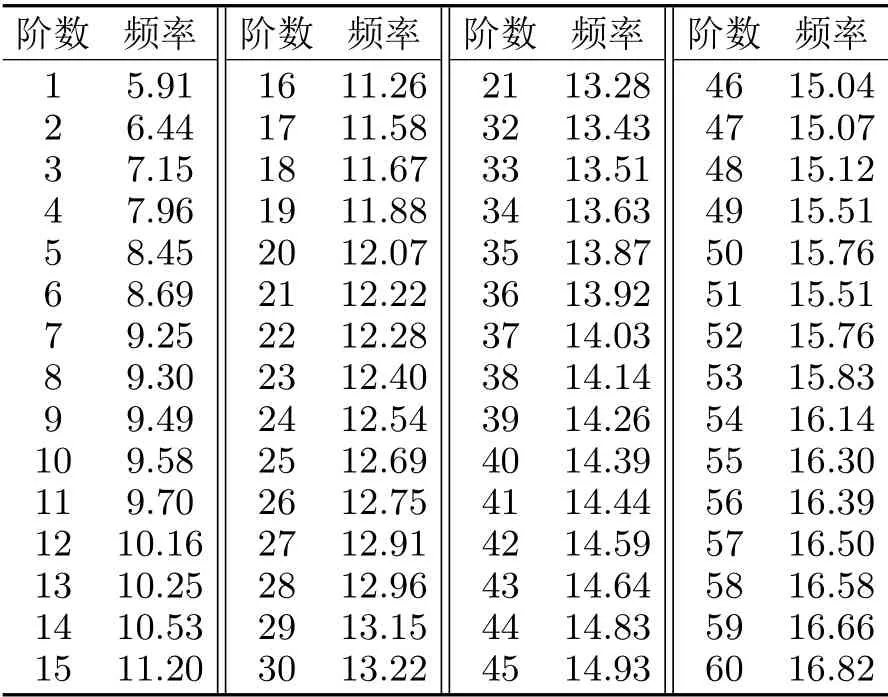
表1 阵面阵架模态计算结果Hz

由表1和图3可见，阵面阵架的模态非常丰富，而且模态频率密集度较高，大部分都是局部模态。1阶和5阶模态主要表现为加强架的横向振动，2阶、3阶、4阶和6阶模态主要表现为阵面阵架开口处的局部振动。

3 多体动力学分析

3.1 多体动力学模型

为评估机械阵上水平/垂直滑车在运动过程中对机械阵的影响，需建立阵面阵架、机械阵、导轨、目标和干扰源滑车的多体动力学模型并对其工作过程进行分析。多体动力学模型中需建立阵面阵架、机械阵和导轨的柔性体模型。柔性体模型的建立过程为：在所建立的有限元模型的基础上进行一系列的相关定义后生成有限元模型输入文件，提交给有限元求解器进行模态计算，自动生成多体动力学模型所需的模态中性文件，最后在多体动力学平台中使用柔性体接口程序读取模型中性文件来构建阵面阵架、机械阵和导轨的柔性体模型[7-9]。

多体动力学模型中表示弹性体的方法是模态综合法。模态综合方法是一种特别有效的减少自由度的方法，其基本思想是赋予柔性体一个模态集，采用模态展开法，用模态向量和模态坐标的线性组合来表示弹性位移，通过计算每一时刻物体的弹性位移来描述其变形运动[10-14]。

模态综合法有多种理论及计算方法，本文采用的是Craig-Bampton方法，定义弹性体的广义坐标为：

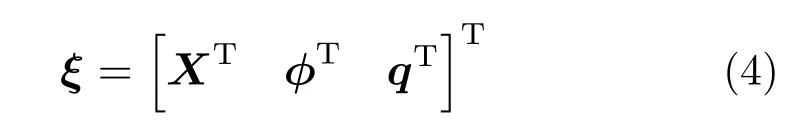
式中：X表示在全局坐标系下，全局坐标系坐标原点到柔性体局部坐标系坐标原点的位置矢量；φ表示方位欧拉角；q表示模态坐标。

在广义坐标下，运用拉格朗日乘子法建立柔性体的运动微分方程：

基于Craig-Bampton模态综合法，建好的阵面阵架多体动力学模型见图4，机械阵、目标和干扰源滑车模型见图5。

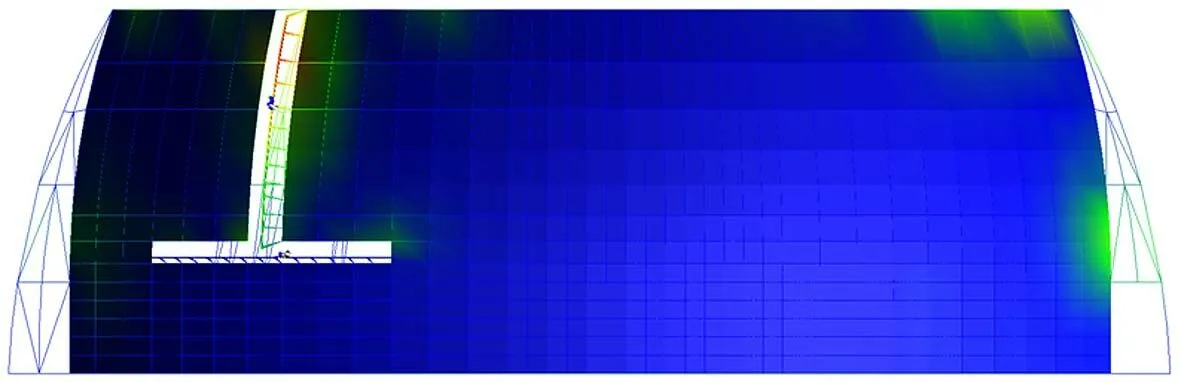
图4 阵面阵架多体动力学模型

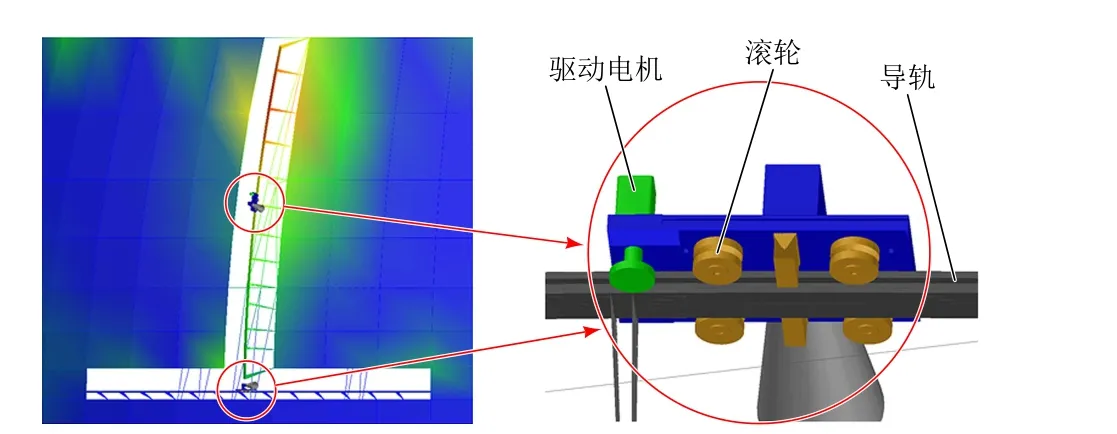
图5 机械阵、目标和干扰源滑车模型

模型中目标和干扰源滑车上的滚轮与导轨间的约束关系采用接触约束力来实现。接触过程中考虑了库仑摩擦效应，接触约束力计算公式为[15-18]：

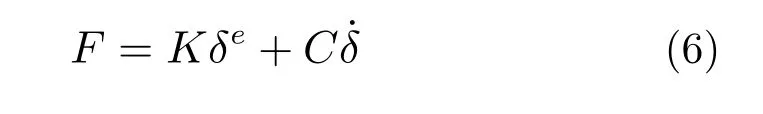
式中：K为刚度系数；C为阻尼系数；e为非线性指数；δ和˙δ分别为穿透深度和穿透速度。接触约束力参数取值如表2所示。

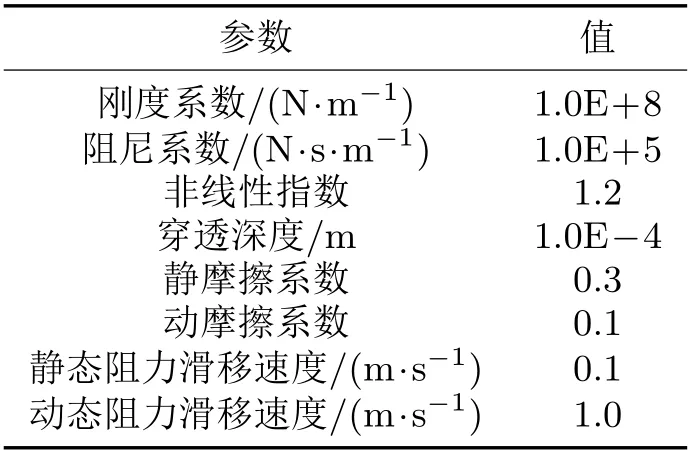
表2 接触约束力参数取值

3.2 计算结果及其分析

在目标和干扰源滑车驱动电机处施加运动驱动，让滑车在0.2 s内加速到1.5 m/s，然后匀速运动。仿真计算结果见图6和图7。

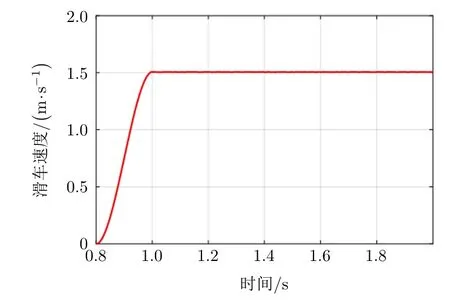
图6 滑车速度曲线

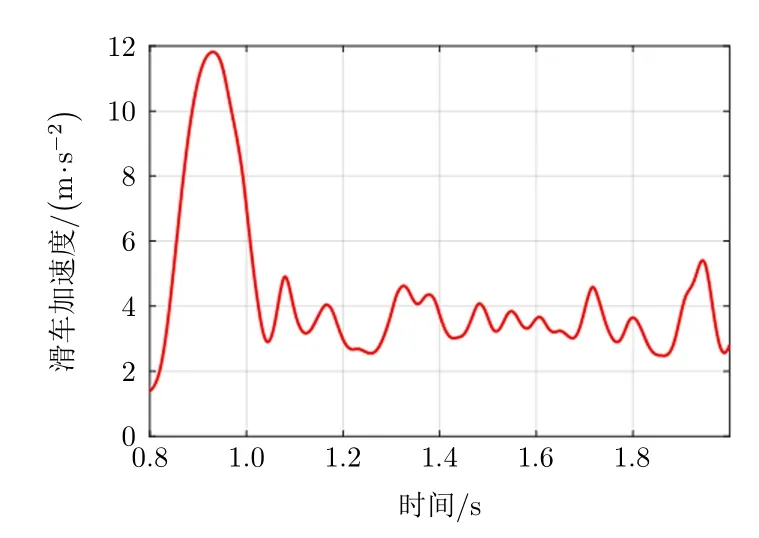
图7 滑车加速度曲线

从图6和图7可以看出，目标和干扰源滑车在机械阵上加速和匀速运动过程中，加速度不大于12 m/s2，速度不大于1.5 m/s，满足射频仿真试验过程中阵面阵架上目标和干扰源在空间实时运动模拟的要求。图8为阵面开口处上端位移曲线，图9为阵面阵架开口处振动响应曲线。从图8和图9可以看出，目标和干扰源滑车运动过程中，阵面上端的振动位移和振动响应都很小，振动位移不大于0.03 mm，振动加速度不大于1.5 m/s2，满足射频仿真试验过程中目标和干扰源的空间位置精确定位要求。

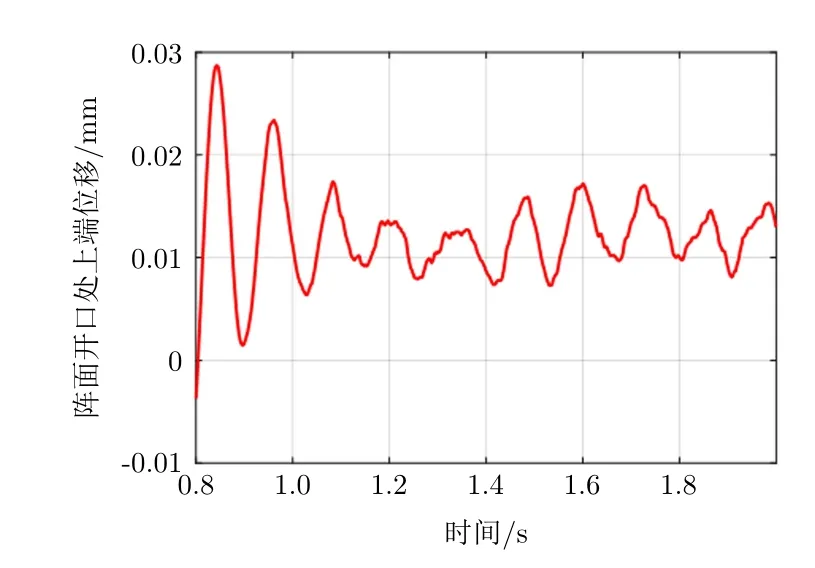
图8 阵面开口处上端位移曲线

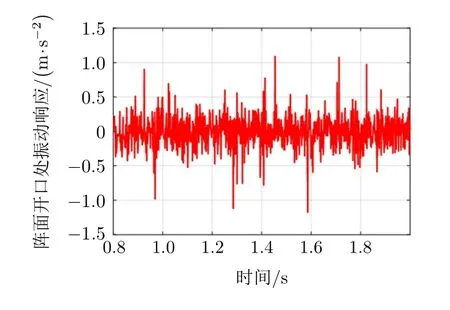
图9 阵面阵架开口处振动响应曲线

4 试验验证

根据阵面阵架结构设计和动力学仿真结果，在实验室中安装和调试了阵面阵架实物模型，如图10所示。在机械阵上开展了多次目标和干扰源滑车在水平和垂直方向的跑动试验，以测试阵面阵架的动态性能。

图10 阵面阵架实物图

试验过程中，通过控制、调整水平和垂直导轨上滑车的驱动电机，让滑车在1 s内从静止加速到1.5 m/s，然后以1.5 m/s的速度匀速运动1 s，最后在1 s内减速到静止。滑车加速过程中，测试阵面阵架上端开口处的振动响应。多次试验结果表明，滑车加速和减速过程中，阵面阵架上端开口处的振动位移不大于0.1 mm，振动响应加速度不大于1.0 m/s2，阵面阵架几乎没有任何晃动，各部件的刚度以及目标和干扰源的空间位置精确定位满足设计要求。

5 结束语

在建立大型柔性阵面有限元模型的基础上，对阵面阵架进行模态分析，构建目标和干扰源滑车在机械阵上运动的多体动力学模型，研究滑车在机械阵上加速和匀速运动对阵面阵架的影响。研究结论如下：

1）目标和干扰源滑车在机械阵上的运动速度不大于1.5 m/s，加速度不大于12 m/s2，满足装在滑车上的目标和干扰源的空间实时运动模拟要求；

2）滑车实时运动模拟过程中，阵面上端的振动位移和振动响应都很小，满足目标和干扰源的空间位置精确定位要求；

3）根据仿真结果研制的阵面阵架实物模型各部件的刚度以及目标和干扰源的空间位置精确定位满足设计要求。