某机载雷达的隔振系统性能研究*
徐兴盛,刘 斌,朱 晨,杨 新
(中国电子科技集团公司第二十二研究所,山东 青岛 266107)
引 言
近些年,随着雷达技术的飞速发展,越来越多的军用或民用雷达被安装在飞机上使用。飞机在飞行过程中会产生各种振动载荷,如果机载雷达的机械环境适应能力差,则一方面雷达会因振动作用而产生机械故障,另一方面雷达稳定性可能会下降。因此,机载环境的隔振系统设计是实际工程中必须考虑的问题。为隔振系统选择合适的隔振器通常会产生良好的隔振效果。如果隔振器选择错误,往往会导致机载雷达损坏,造成严重后果。
隔振系统设计一直是学术研究的热点,国内外的科研人员对此进行了大量研究。文献[1]提出了一种以凸轮-滚轮-非线性弹簧机构作为负刚度结构的准零刚度隔振器,在负刚度结构中对称设计了两个水平阻尼器;文献[2]采用粘弹性-超弹性-弹塑性材料本构模型,对一种新型的橡胶隔振器进行了动态特性研究,并与已有实验结果进行了对比;文献[3]针对某精密仪器的橡胶隔振器进行了动态特性研究,验证了隔振器非线性动力学模型的正确性和有效性;文献[4]设计出一种多维被动隔振平台,通过仿真证明了隔振平台在失效情况下能够保护雷达不失去工作能力。此外,文献[5-11]对机械结构的减振、隔振器的设计等进行了相关研究。
为了解决隔振系统隔振参数的选取问题,获得满足隔振要求的隔振参数,本文以实际工程中某机载雷达的隔振系统为例,通过对比仿真计算、理论计算和实验数据,验证了仿真计算结果的准确性和可靠性。
1 研究对象介绍
某机载雷达在直升机上的安装方式如图1所示。机载雷达固定在特制的挂架上,挂架与直升机接口之间有4个隔振器。已知机载雷达的质量为32 kg,挂架选用高强度铝合金材料,质量为1.3 kg。构建隔振系统结构的力学仿真模型,见图2。将机载雷达看作一个刚体,隔振系统主要由挂架和4个隔振器构成,雷达的质量以质点形式分布在挂架的6个雷达安装孔上,保证隔振系统整体满足实际工程质量要求。
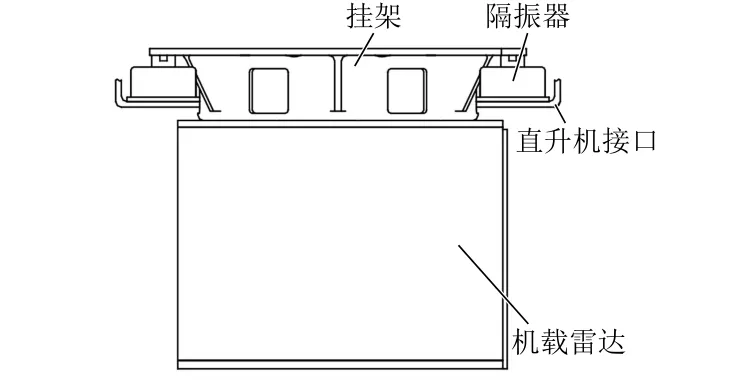
图1 某机载雷达的结构示意图
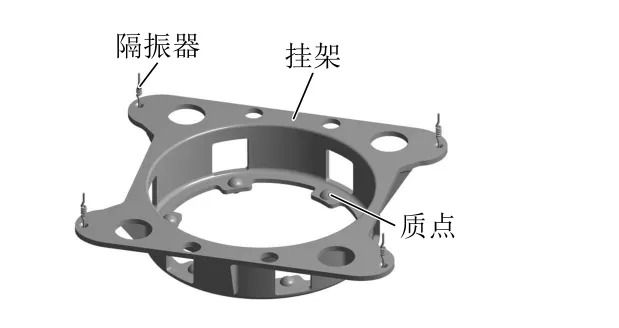
图2 隔振系统的随机振动分析模型
直升机载机平台舱内设备的振动频谱范围为10~500 Hz。根据《GJB 150.16A—2009军用装备实验室环境实验方法第16部分:振动试验》中表C.4和图C.10获得随机振动中直升机的加速度功率谱密度曲线,如图3所示。将图3的曲线作为隔振系统的输入激励。
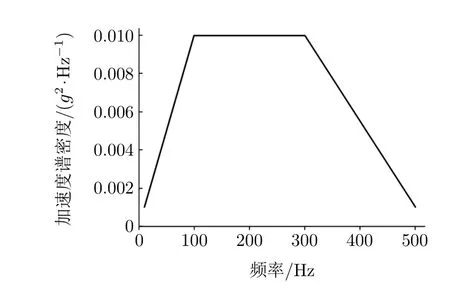
图3 随机振动环境的加速度功率谱密度
2 理论分析与计算
2.1 隔振理论
当机载雷达吊装在飞机上时,将其假设为一个刚体,则该系统可以简化为一个单自由度的被动隔振力学模型,见图4。
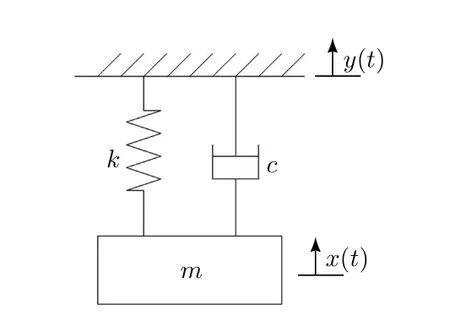
图4 隔振的力学模型
机载雷达质量为m,它通过阻尼系数为c、刚度为k的隔振器与基础相连,基础受到激励y(t)的作用。机载雷达的运动方程为:
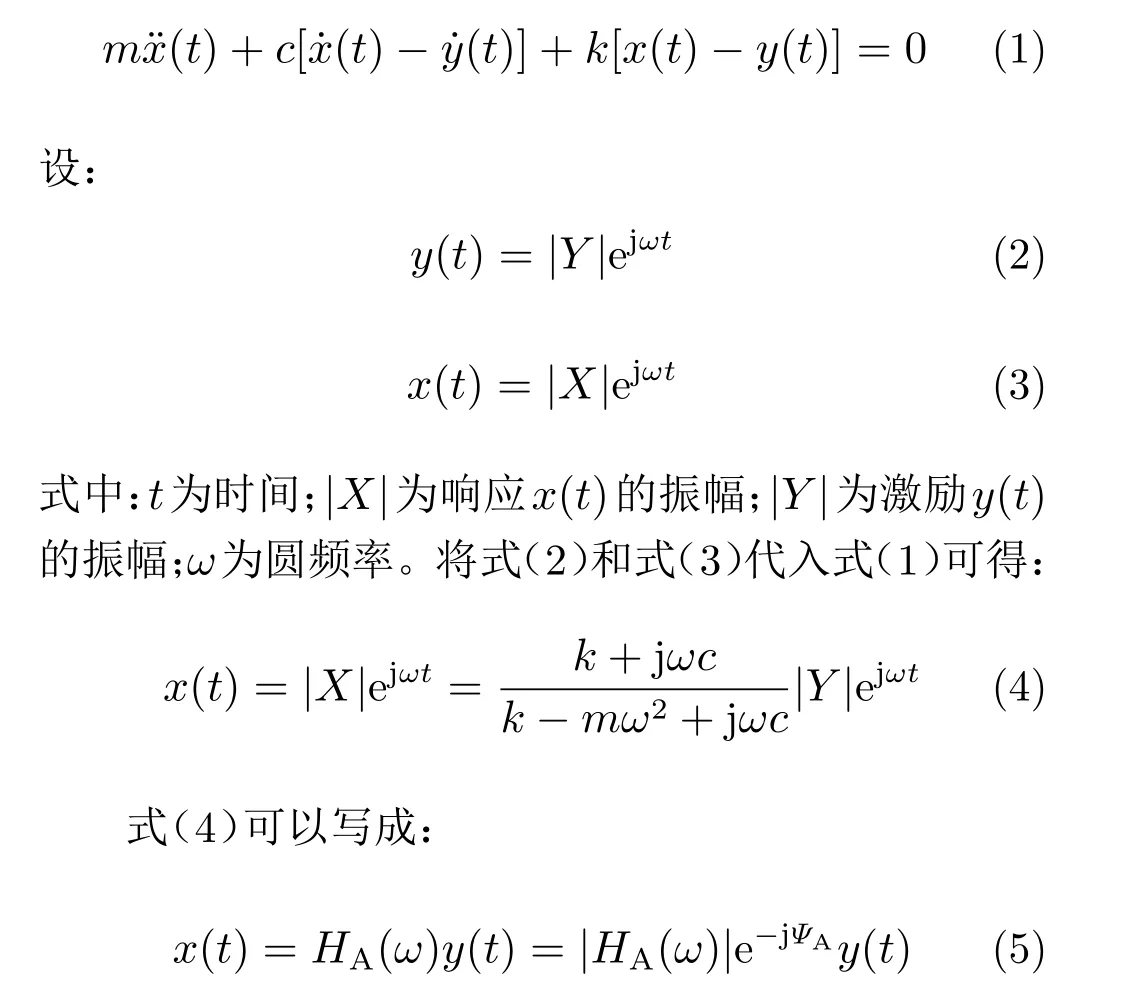
式中:HA(ω)为隔振的频率响应函数;ΨA为隔振的初相角。
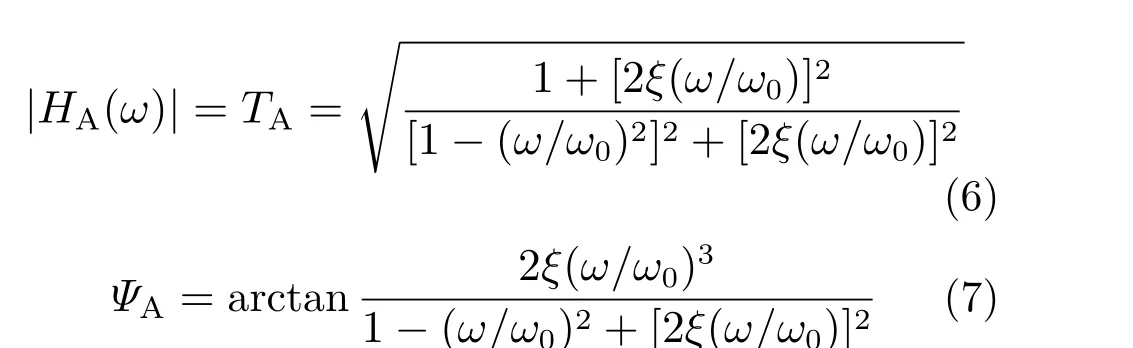
式中:TA被称为隔振的传递率,表示在力学模型中隔振的效果,TA越小,模型的隔振效果就越好;ξ为阻尼比;ω0为系统无阻尼的自振圆频率。
2.2 加速度谱激励的随机振动
振动系统受基础加速度¨y(t)的作用,运动方程可写为:

3 仿真分析与计算
在隔振系统中输入如图3所示的加速度功率谱密度激励。选取系统的阻尼比ξ为0.2,在刚度k为100 N/mm,400 N/mm和800 N/mm的3种工况下,得到图5所示的隔振系统输出的相对加速度功率谱密度的理论值和计算值以及图6所示的输出的相对位移功率谱密度的理论值和计算值。由图5可见,当刚度相同时理论值和计算值的拟合曲线非常接近。
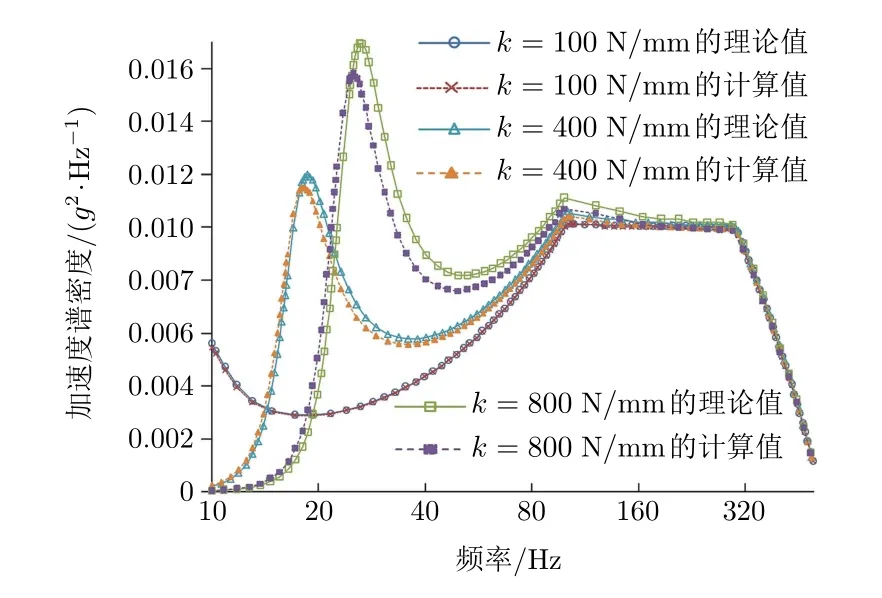
图5 相对加速度功率谱密度(ξ =0.2)
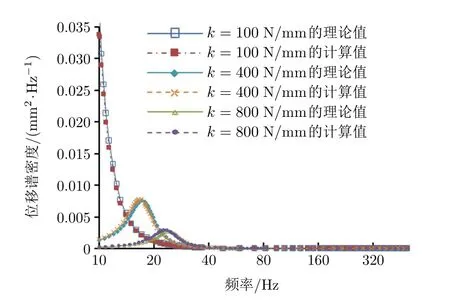
图6 相对位移功率谱密度(ξ =0.2)
误差E定义为:
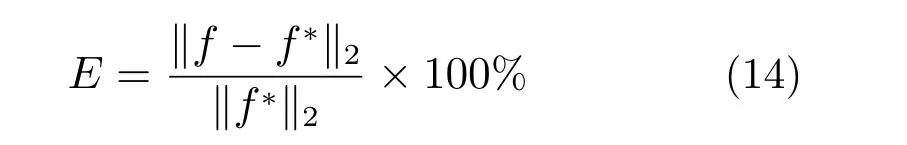
式中:f∗为选取频点的理论值序列;f为选取频点的计算值序列。
当刚度为100 N/mm,400 N/mm和800 N/mm时,根据公式(14)可得计算值与理论值的误差分别为0.42%,2.33%和5.64%。因此,随着刚度k的增大,仿真计算的相对加速度功率谱密度的误差逐渐增大。
由图6可见,对于不同的刚度k,隔振系统输出的相对位移功率谱密度计算值和理论值的拟合曲线也非常接近。当刚度为100 N/mm,400 N/mm和800 N/mm时,根据公式(14)可得计算值与理论值的误差分别为5.84%,8.61%和17.34%。因此,随着刚度k的增大,仿真计算的相对位移功率谱密度的误差也有增大的趋势。
现在考虑阻尼比ξ对系统计算结果的影响。在隔振系统中同样输入如图3所示的加速度功率谱密度激励。选取刚度k为400 N/mm,在阻尼比ξ为0.1,0.2和0.3的3种工况下,得到图7所示的隔振系统输出的相对加速度功率谱密度的理论值和计算值以及图8所示的输出的相对位移功率谱密度的理论值和计算值。由图7可见,当阻尼比ξ相同时,理论值和计算值的拟合曲线非常接近。当阻尼比ξ为0.1,0.2和0.3时,计算值与理论值的误差分别为6.65%,2.33%和1.70%。随着阻尼比ξ的增大,理论值和计算值的误差逐渐减小。
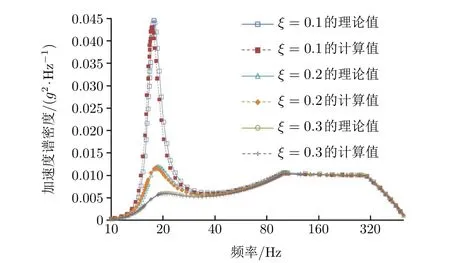
图7 相对加速度谱密度(k =200 N/mm)
由图8可见,对于不同的阻尼比ξ,隔振系统输出的相对位移功率谱密度计算值和理论值的拟合曲线非常接近。理论值和计算值的平均误差分别为13.72%、8.61%和6.58%。随着阻尼比ξ的增大,理论值和计算值的误差逐渐减小。
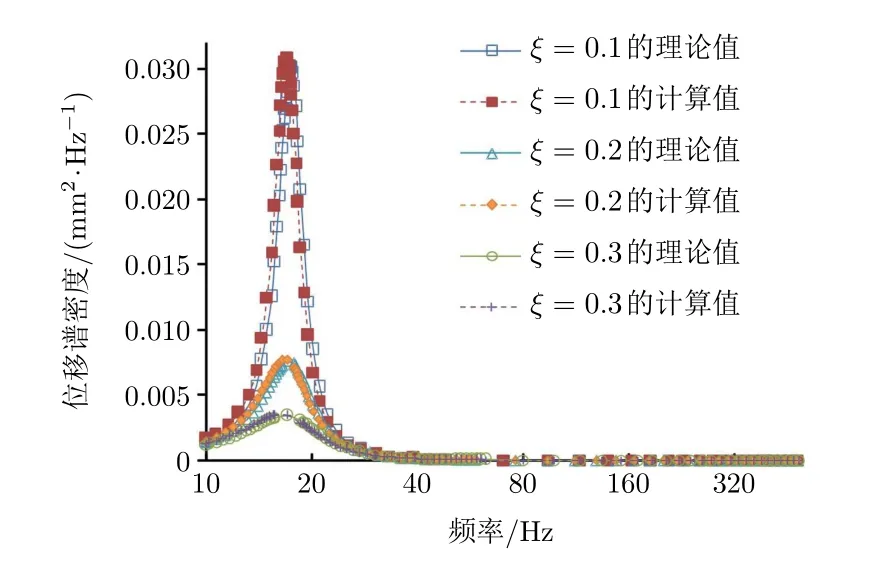
图8 相对位移功率谱密度(k =200 N/mm)
4 分析与对比
4.1 仿真结果分析与对比
对比图5和图6不难发现,在10~120 Hz左右的低频率范围内,加速度功率谱密度和位移功率谱密度的求解数值差距较大,随着频率的增加,它们的求解数值逐渐接近,所以刚度k对低频段的影响相对较大。此外,在3种工况条件下,隔振系统的理论固有频率分别为8.856 Hz,17.443 Hz和24.669 Hz。当刚度k为400 N/mm和800 N/mm时,隔振系统的固有频率在10~500 Hz的激励范围内,从图中可以看出,系统在它们的固有频率处出现峰值。随着刚度k的增大,加速度功率谱的峰值有增大的趋势,而位移功率谱的峰值则相反。
对比图7和图8不难发现,在10~100 Hz的低频率范围内,相对加速度功率谱密度和相对位移功率谱密度的求解数值差距较大,随着频率的增加,它们的求解数值逐渐接近,所以阻尼比ξ对低频段的影响较大。此外,在3种工况条件下,隔振系统的理论固有频率为17.443 Hz,从图中可以看出,系统在固有频率17.443 Hz处出现峰值。随着阻尼比ξ的增大,加速度和位移的功率谱密度的峰值有增大的趋势。
对比分析表明,本文描述的仿真分析方法在不同刚度k和阻尼比ξ的条件下,具有较高的精度和可靠性。
4.2 实验分析与对比
将隔振系统放置于振动台上,输入图3的谱密度曲线进行实验验证。隔振系统中隔振器选择JSZ-2型号。实验中,分别用加速度传感器监测了振动台和托架的加速度响应值。隔振器JSZ-2的性能参数如下:载荷为9 kg;静变位为(6±1)mm;质量为0.142 kg;刚度为28.8 N/mm;阻尼为0.34 N·s/mm。
经计算,该隔振系统的固有频率为9.296 Hz,阻尼比为0.347。图9为通过仿真计算、理论计算和实验数据获得的相对加速度谱密度。由图9可见,隔振系统输出的相对位移功率谱密度计算值和理论值的拟合曲线非常接近,实验数据获得的相对加速度谱密度与理论计算值有一定的偏差,但趋势基本相同。根据公式(14)可得计算值、实验值与理论值的误差分别为9.54%和22.60%。实验表明,本文描述的仿真分析方法具有较高的精度和可靠性。
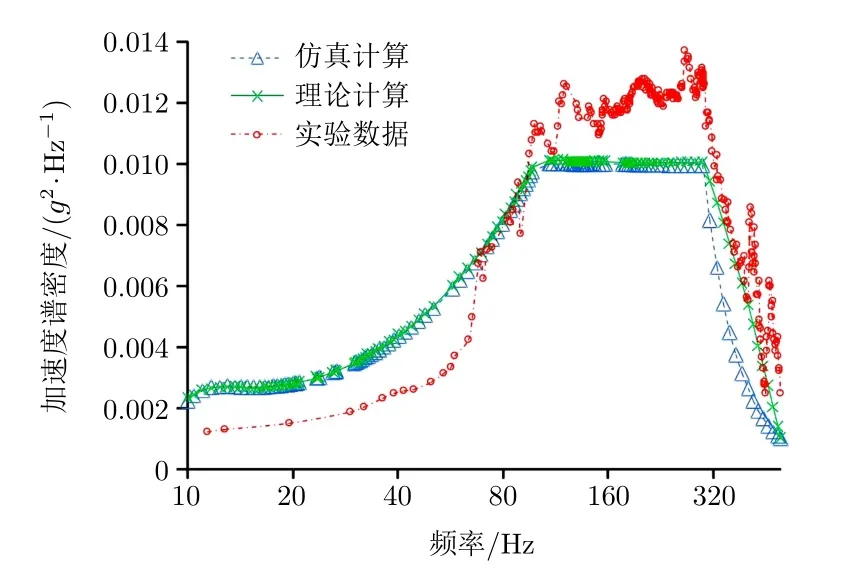
图9 相对加速度谱密度
5 结束语
本文以某机载雷达的隔振系统为例,研究了隔振器对隔振性能的影响,主要工作及结论如下:
1)通过分析隔振系统激励输出功率谱的理论值和计算值可知,本文的仿真分析方法在不同刚度k和阻尼比ξ的条件下具有较高的精度和可靠性。
2)通过实验数据和理论计算验证了该仿真分析方法的正确性,满足隔振设计的要求。
3)该仿真分析方法可用于获取满足隔振要求的隔振参数。

