基于ANSYS的浮空器组阵结构屈曲分析及优化设计*

高 翔，张 烁，张贝贝，何 仁

（西安电子科技大学电子装备结构设计教育部重点实验室，陕西 西安 710071）

引 言

空间太阳能电站的概念由美国科学家彼得·格拉赛博士于1968年提出。该设想是将太阳能电池阵发射到太空，聚集大量阳光并完成光电转换，继而将产生的电能以微波的形式传输到地球上，经天线接收整流后转变成电能供人类使用。目前，空间太阳能电站项目地面演示系统“逐日工程”的试验场建立在西安电子科技大学南校区。当前“逐日工程”试验系统主要由太阳能高倍聚光器、光电转换与电力管理系统以及无线传能的收发天线系统三大功能系统组成[1]。

本文提出了一种空间浮空器组阵系统，用来承载球形太阳能反射面、发射天线等相关载荷，在空中实现悬停，进而与地面进行微波传能试验。大型空间结构的失效往往是因为结构失稳，而不是达到强度极限[2]。因此针对该系统，利用ANSYS有限元软件建立其桁架结构三维模型，并验证其结构稳定性，进而对其型材截面尺寸进行结构优化，实现轻量化的设计目标[3]，增强系统的载重能力。

1 结构方案

高空气球系统具有成本低、易于施放等优势，广泛应用于通信中继、环境监测等领域。目前，高空气球承载工作载荷的方式主要为悬吊式，如图1所示。

图1 悬吊式载荷示意图

“逐日工程”试验项目如果采用悬吊形式，球形太阳能反射面会被气球遮挡，大大降低了系统的能量收集效率。而且工作载荷质量较大，导致单一气球的体积十分巨大，这对材料强度、制造成本以及定位控制提出了极大挑战。

针对上述问题，本文提出气球组阵结构，总体由支撑桁架结构和4个高空气球组成。其中，桁架支撑结构由上下两个环形底框和4根圆周方向上均布的立柱构成。球形太阳能反射面安装于上底框，可以提高太阳能的收集率；发射天线安装于下底框，便于与地面接收天线进行收/发试验。每个高空气球通过上下两根绳索与桁架支撑结构相连，以保持系统的稳定性。支撑桁架结构上安装有推力螺旋桨，可以实现姿态控制，提高系统的抗风性，进而在空中实现稳定悬停。组阵系统整体结构如图2所示。上下底框为双圈六面体环形桁架，外圈直径为10 m，结构如图3所示。

图2 空间大型浮空器组阵系统整体示意图

图3 双圈六面体环形桁架

4根立柱为四棱柱单元桁架结构，高度为8 m，分别与上下底框连接。立柱与底框连接结构见图4。

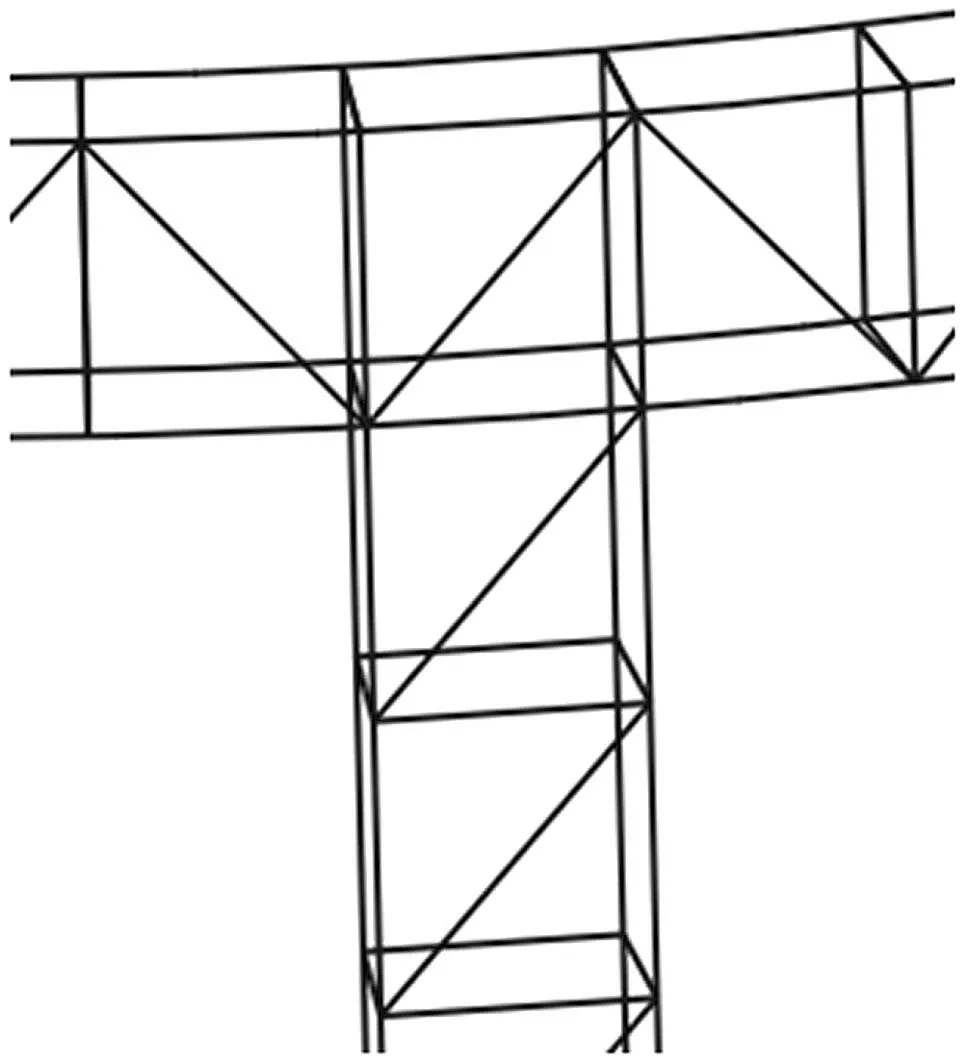
图4 立柱与底框连接结构

2 有限元模型建立

利用有限元软件ANSYS Workbench Design Modeler建立立柱结构三维模型[4]，如图5所示。桁架材料为铝合金，密度为2 770 kg/m3。立柱结构的总长度为8 m，单元长度为0.5 m，共16个单元。桁架截面形状近似为等腰梯形，上底长a= 410 mm，下底长b=438 mm，高h=300 mm。

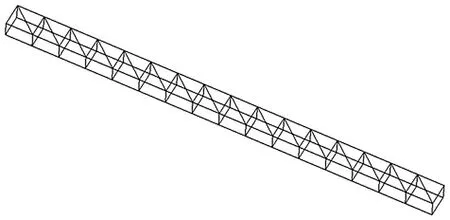
图5 立柱桁架结构三维模型

采用beam188 梁单元进行有限元分析计算，梁单元截面形状为“L”形，设置初始横截面边长l=15 mm，厚度t=1.5 mm。

2.1 桁架结构静力分析

在地面稳定停靠状态下，上底框承受竖直向下的载荷共计12 000 N，近似以节点力的方式作用在4根立柱的16个顶点上，每根立柱承受3 000 N的作用力。因此，对单根立柱顶端4个顶点各施加750 N竖直向下的作用力，对立柱下端4条边施加固定约束，求解出立柱结构的总应变和应力云图，如图6所示。

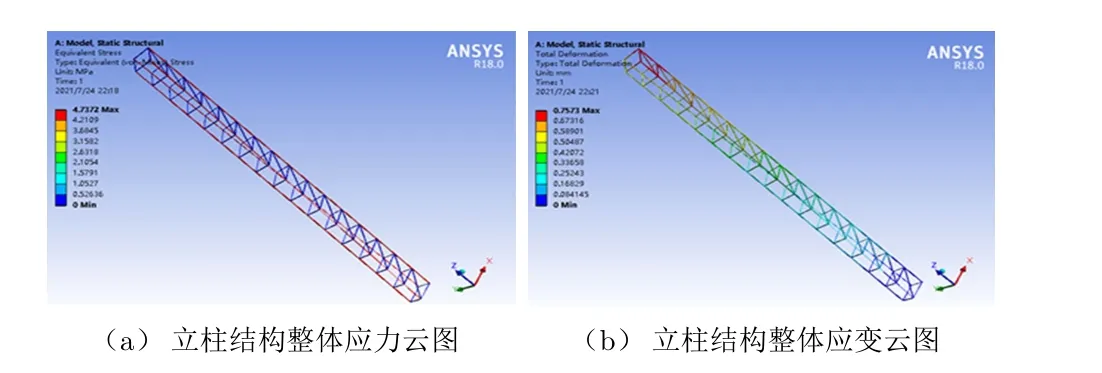
图6 立柱结构整体应力及应变云图

2.2 强度校核和刚度校核

2.2.1 强度校核

根据图6的计算结果，桁架整体最大综合应力σs=4.73 MPa。桁架结构使用的材料为铝合金材质，其许用应力[σs]远大于桁架最大综合应力，因此桁架结构的强度满足要求[5]。

2.2.2 刚度校核

根据图6的计算结果，桁架整体最大应变位移δmax=0.757 3 mm，远小于实际工作中桁架结构的许用应变位移[δ]，因此桁架结构的刚度满足要求。

3 桁架结构屈曲分析

3.1 结构屈曲基本概念

在载荷作用下，结构因材料的弹性性能而发生变形，若变形后结构上的载荷保持平衡，这种状态称为弹性平衡。如果结构在平衡状态时受到扰动而偏离平衡位置，当扰动消除后仍能恢复原来的平衡状态，这种平衡状态称为稳定平衡状态；如果即使扰动消除，结构仍不能恢复原来的平衡状态，而是在新的状态下平衡，则原来的平衡状态就成为不稳定平衡状态。当结构所受载荷达到一定值时，一个微小的增量就使结构平衡状态发生很大的改变，这种现象叫做结构屈曲，此时构件还没有达到屈服就丧失了承载力[6]。

3.2 屈曲分析的理论基础

在平衡状态时，考虑轴向力和中面内力对弯曲变形的影响，根据势能驻值原理得到结构的平衡方程为[6]：

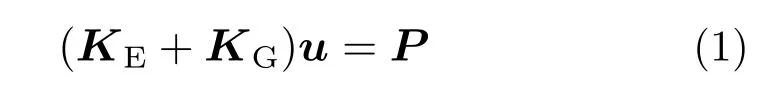
式中：KE为结构弹性刚度矩阵；KG为结构几何刚度矩阵；u为节点位移向量；P为节点载荷向量。

式中：δ2(·)表示二阶变分；λk为第k阶的特征值。线性屈曲分析就是解该特征值，即第k阶临界载荷系数。通过有限元软件ANSYS解上述方程可以计算出λk，则第k阶临界屈曲载荷P=λkP0[4,8]。

3.3 屈曲分析

得到结构的静力解后，通过屈曲分析可以得到结构屈曲特征值。工业领域通常关注结构的前6阶屈曲模态，但桁架支撑结构在达到更高的屈曲载荷之前便已经遭到破坏，因此这里最为关心的还是第1阶。屈曲分析得到的各阶特征值以及计算得到的各阶临界屈曲载荷如表1所示。

表1 前6阶模态的特征值和临界屈曲载荷

这里，第1阶临界载荷约为12 kN，满足3 kN的设计需求。因此，立柱结构的稳定性符合要求。

4 桁架结构优化设计

4.1 优化问题模型建立

以第1阶临界屈曲载荷为约束条件。因为几何结构和材料密度一定，所以优化总体积等效于优化总质量。因此，对桁架梁截面的型材进行尺寸结构优化，通过响应曲面分析和多目标遗传优化算法找到设计优化点，使优化尺寸既能满足临界屈曲载荷的要求，又能减少材料，达到降低成本的目的。

首先建立优化问题模型：

式中：W代表整个结构的质量；λcr为特征值的约束条件，它是第1阶临界屈曲特征值。

采用ANSYS Workbench中的Design Exploration模块为优化工具，以桁架适用型材的截面尺寸，即型材横截面边长l（输入参数为P1）和厚度t（输入参数为P3）作为输入参数，以质量W（输出参数P5）和1阶模态屈曲特征值λ（输出参数P6）作为输出参数，建立优化结构模型。试验类型为拉丁超立方抽样设计方法，样本类型为中心复合设计方法，得到的设计点优化情况如表2所示。

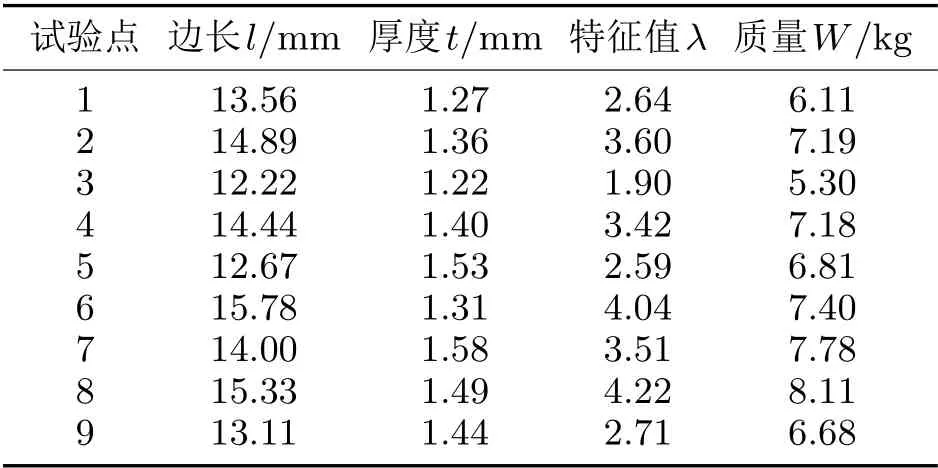
表2 试验点具体参数值

4.2 响应曲面分析[7]

响应面设计方法能够结合试验设计、数理统计以及回归分析，运用合理的试验设计方法采集少量样本，通过多元回归方程来拟合输入参数（因素）与输出参数（响应值）之间的隐函数关系，并通过回归分析来寻求最优设计点。响应面法是解决多变量问题的一种统计方法。

分别以质量W和1阶模态屈曲特征值λ作为响应值，建立3D响应曲面图，观察两个响应值随输入参数的变化趋势，如图7所示。

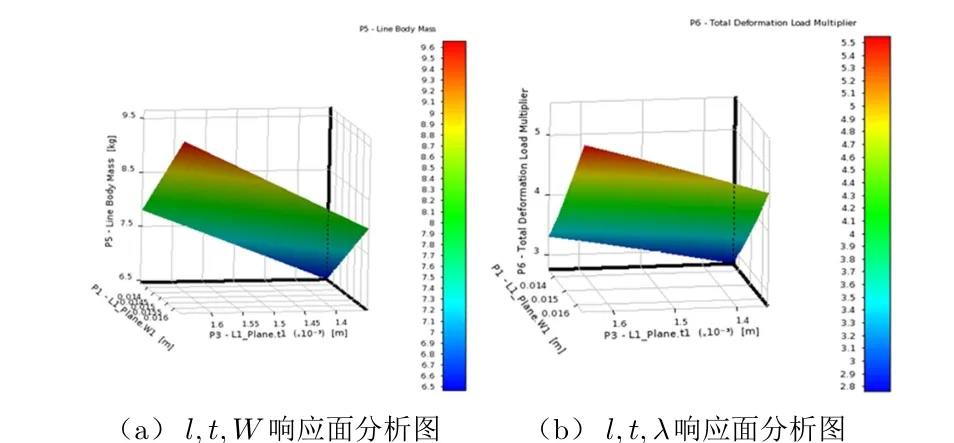
图7 l,t,W 及l,t,λ响应面分析图

由图7可知，随着型材截面尺寸l,t的增大，响应值质量W和1阶屈曲特征值λ也随之增大，W和λ均与l和t呈线性关系。因此，需要寻找设计点，使其既能满足一定的稳定性要求，又能够实现最大程度的轻量化设计，进而提高系统的载重能力[8]。

4.3 多目标遗传优化算法

响应面分析直观展示出输入参数与输出参数的关系，而多目标遗传算法（Multi-Objective Genetic Algorithm, MOGA）可以在响应面模型的基础上进行循环优化迭代，可避免每次都调用仿真模型，显著地提高了计算效率。在支持多目标和多约束的条件下，随着响应面模型的不断更新，寻找Pareto最优解集[9]，直至优化算法实现收敛。

在ANSYS Workbench Design Exploration平台中选择多目标遗传优化算法MOGA，设置初始样本点为500，每次迭代的样本数设置为100，设置约束为1阶屈曲特征值λ ＞3.8，设置优化目标为结构质量W的最小值。求解出的3组候选优化设计点与初始点对比如表3所示。

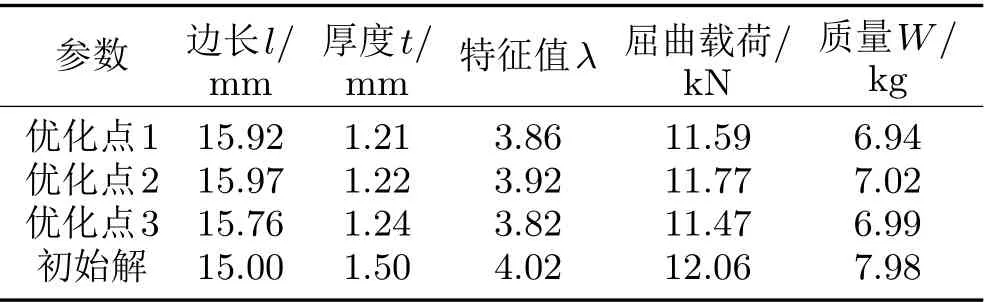
表3 优化设计点参数

由表3可知，得到的3个优化设计点在满足结构稳定性的前提下，总体质量都有所下降。选择优化点3作为最终解，并对其强度和刚度进行验证。优化后的立柱结构减重13.03%，满足轻量化设计需求，这对载重浮空器系统有十分重要的意义。

5 结束语

本文针对“逐日工程”特殊的工作载荷，提出了一种创新型气球组阵系统，解决了目前浮空器悬吊式载荷存在的问题。针对此空间结构进行了屈曲分析，验证了该浮空器系统立柱结构的稳定性。采用拉丁超立方设计方法建立了质量和屈曲特征值的响应面模型，并通过多目标遗传优化算法进行了结构的尺寸优化，最终在满足稳定性条件的前提下，实现减重13.03%。

在轻质材料研究难度日益增大的情况下，结构的轻量化成为航空航天领域的重点。结构优化一方面可以降低能耗，另一方面则有利于最大程度地完成复杂度高、任务载荷巨大的空中试验。因此，对“逐日工程”试验而言，结构轻量化的探索势在必行。