加劲钢板在荷载作用下的屈曲模式分析

李 云 帆

(西安科技大学力学系，陕西 西安 710054)

0 引言

目前，我国的基础设施建设正在如火如荼的进行当中，特别是公路以及桥梁的建设，对某些地区的经济发展尤为重要。在基础设施建设中，桥梁工程的整体难度及要求均非常高，这就对工程中所用到的工程材料有了很高的要求，加劲钢板正是其中的代表。加劲钢板在桥梁、机械和船舶等工程中都有着非常重要的应用，其具有强度高、重量轻等特点。

对于加劲板屈曲的研究已有很长的历史。Troitsky[1]最早开启了加劲板稳定性、屈曲及振动的分析。Timoshenko[2,3]给出了矩形板在横向肋条和纵向肋条加劲情况下的稳定性分析。Seide[4]创造性地把加劲杆的偏心效应当作其有效惯性矩来看。Cox和 Riddel[5]将应变能方程引入多重加劲杆的讨论。Stiffel[6]和Massonnet[7]对纯弯曲作用下的加劲板进行了研究。目前，通常采用有限元方法进行加劲板的屈曲分析，本文采用的是基于MATLAB的约束有限元计算程序。本文中，首先分析了各向同性矩形钢板在不同条件下的屈曲，并将结果与ANSYS所得结果进行对比，以验证所用约束有限元计算程序的可靠性；其次,对平均分布纵向肋条加劲的矩形板在均布压力下所产生的不同屈曲模式进行研究与分析。

1 无加劲肋条、各向同性矩形板的屈曲分析

本章对四面简支、两侧受均布压力的无加劲各向同性矩形板进行屈曲分析。其边界条件及荷载情况如图1所示。

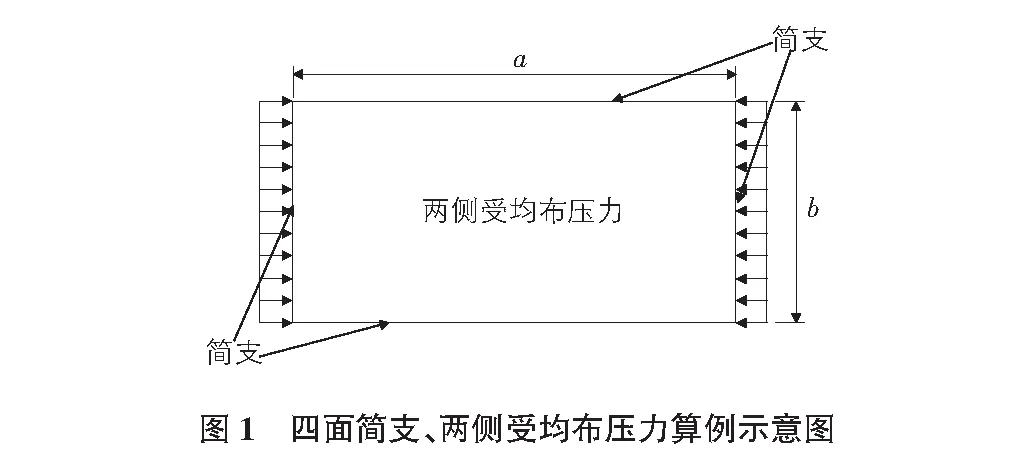
图中a与b分别为矩形板的长度(纵向)与宽度(横向)，计算中其余参数见表1。

表1 计算模型参数表

根据Theories and Applications of Plate Analysis[8],本问题的解析解如式(1)所示：

(1)

其中,m为沿矩形板纵向的屈曲模态阶数；n为沿矩形板横向的屈曲模态阶数；D为矩形板的抗弯刚度，N·m2。

本问题的约束有限元法与ANSYS计算的结果及误差见表2。

如表2中所示，约束有限元法的平均误差为2.48×10-4，ANSYS的平均误差为1.33×10-2。可以看出，约束有限元法的计算误差比ANSYS计算误差要小得多。

2 屈曲模式特点以及判定标准

屈曲模式可分为整体屈曲(Global Buckling)，局部屈曲(Local Buckling)，扭曲屈曲(Distortional Buckling)以及其他屈曲模式。其中整体屈曲、局部屈曲和扭曲屈曲所占百分比之和非常接近屈曲变形的全部，因此只要将这三种屈曲模式所占百分比分析清楚，就能够对屈曲变形进行精确的描述。整体屈曲的特点是：在屈曲过程中，构件的横截面不发生变形，作为刚体移动[9]。局部屈曲的特点是：构件的各部分同时屈曲，相邻板件的夹角保持不变，且相交的棱线保持挺直[10]。扭曲屈曲介于整体屈曲与局部屈曲之间。

以上三种屈曲模式的横截面变形见图2。

加劲板的横截面如图3所示，Y轴方向为加劲板纵向，X轴方向为加劲板横向，均匀分布的加劲肋在YOZ平面内。

各种屈曲模式在图3的坐标系下有如表3所示的屈曲模式判定标准。

3 不同屈曲模式的百分比

整体屈曲、局部屈曲和扭曲屈曲各有着不同的判定标准，通过这些标准，能够得到整体屈曲、局部屈曲以及扭曲屈曲在全部屈曲形态中的所占比例。

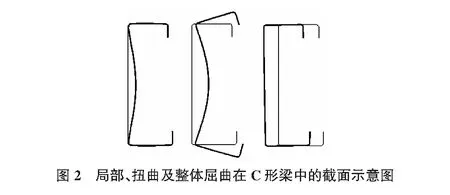
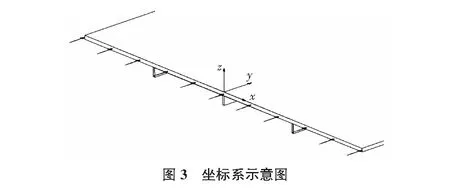
表3 屈曲模式判定表

判定标准整体屈曲扭曲屈曲局部屈曲其他屈曲γxy=0,εx=0,υ线性是是是否εy≠0是是否—κy=0是否——

接下来对两组算例进行研究：两组算例均为矩形加劲板，加劲肋均匀分布。它们的边界条件均为四面简支，荷载为两侧受均布压力作用。计算参数如表4所示。

表4 不同大小加劲肋算例参数表 mm

根据计算结果，得出整体屈曲(GB)、扭曲屈曲(DB)和局部屈曲(LB)三种屈曲模式的百分比随着加劲肋数量变化而变化的趋势，如图4，图5所示。

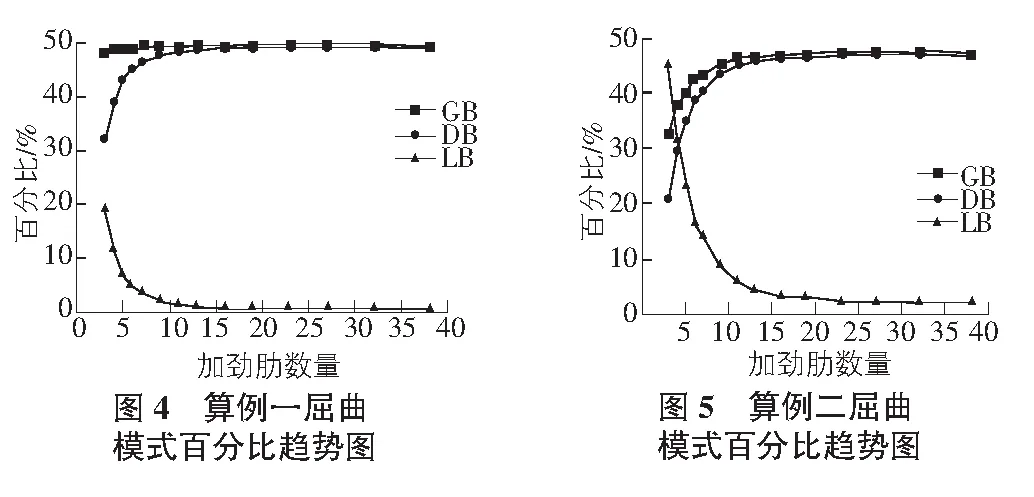
由图4可以看出，算例一中整体屈曲(GB)所占百分比从较少加劲肋到较多加劲肋的变化过程中基本无变化，一直在50%左右。局部屈曲(LB)所占百分比在加劲肋数量增加时，迅速地由19%降低至1%，之后缓慢地逼近0。而扭曲屈曲(DB)与局部屈曲相反，由32%增加至约49%，之后缓慢逼近50%。

由图5可以看出，算例二中整体屈曲(GB)与扭曲屈曲(DB)的所占百分比有着相似的趋势，均随着加劲肋数量的增加而变大，分别由33%和21%增长到约47%。而局部屈曲(LB)由46%迅速降低至4%，之后缓慢降低至2%。

由以上结果可以得出：1)局部屈曲(LB)与加劲肋数量，即加劲肋间距有明显的相关关系。当加劲肋数量变多(即加劲肋间距缩小)时，局部屈曲所占百分比迅速下降。且加劲肋间距与局部屈曲(LB)线性相关，见图6。2)算例一与算例二唯一区别在于加劲肋的大小：算例一使用20 mm×6 mm的加劲肋，算例二使用50 mm×8 mm的加劲肋。当使用较大的加劲肋时，加劲板截面的惯性矩及抗弯刚度均增大。可以看到整体屈曲(GB)和扭曲屈曲(DB)的最大和最小值均变小。其中整体屈曲(GB)和扭曲屈曲(DB)的最大值由算例一(20 mm×6 mm)中的50%降至算例二(50 mm×8 mm)中的47%；最小值分别由算例一(20 mm×6 mm)中的48%和32%降至算例二(50 mm×8 mm)中的33%和21%。3)当加劲肋数量增大到一定程度后，三种屈曲模式的百分比基本稳定。其中整体屈曲(GB)和扭曲屈曲(DB)的百分比基本相等，且在45%～50%之间；局部屈曲(LB)所占百分比最少，在0%～5%之间。

4 结语

本文通过对无加劲肋条各向同性矩形板的计算，验证了所用约束有限元方法的可靠性，其计算精度优于ANSYS软件；其次，介绍了三种屈曲模式(整体、扭曲和局部屈曲)的特点与判定标准；计算结果显示：

1)局部屈曲(LB)所占百分比与加劲肋间距有着非常明显的线性关系；2)当使用尺寸较大的加劲肋时，整体屈曲(GB)和扭曲屈曲(DB)所占百分比均有较大程度的降低；3)当加劲肋增长到一定程度后，三种屈曲模式的百分比基本稳定。其中整体屈曲(GB)和扭曲屈曲(DB)的百分比相等且数值较高，局部屈曲(LB)所占百分比只有不到5%。