黏滞阻尼器在时程分析下的附加有效阻尼比研究

吴 旭， 周美容， 陈 曦， 张雪梅

(1. 南通理工学院 建筑工程学院，江苏 南通 226000； 2. 上海优耐建筑工程咨询有限公司，上海 201908)

在消能减震结构中，阻尼器提供给结构的附加阻尼对结构的地震反应有显著影响，因此，需要准确评估阻尼器的附加有效阻尼比。目前，诸多文献[1-6]提出了黏滞阻尼器在振型分解反应谱分析或时程分析下的附加有效阻尼比的计算方法，但都是建立在一系列假设上，具有局限性，无法准确计算黏滞阻尼器的附加有效阻尼比。本文从阻尼力做功(阻尼能)的角度出发，建立在时程分析下阻尼能与阻尼比的关系，提出黏滞阻尼器附加有效阻尼比的理论计算公式，并建立有限元分析模型来验证公式的正确性。

1 现有附加有效阻尼比计算公式

目前，根据《建筑结构抗震设计规范》(GB 50011—2010)[7]与《建筑减震消能技术规程》(JGJ 297—2013)[8]，阻尼器的附加有效阻尼比ξa可采用下式计算

(1)

式中：Wcj为阻尼器在结构预期层间位移下往复循环一周所消耗的能量;Ws为设置消能部件的结构在预期位移下的总应变能。

本质上，式(1)是由单自由度质点固有阻尼比的原始定义ξ=c/(2mωn)推导出的[9]，但在推导过程中假设质点按自振周期做简谐运动，以阻尼力做功Wc与总应变能Ws代替阻尼系数c、质点质量m以及圆频率ωn来表达阻尼比ξ。因此，这种代替是建立在以下几个前提：①结构为单自由度；②阻尼力与质点运动速度成线性关系；③质点运动模式为简谐运动；④质点简谐运动周期与自振周期相同(共振)；⑤Wcj,Ws分别为质点在简谐运动往复循环一周中的阻尼器所消耗的能量与结构的总应变能。

在实际工程中，通常采用式(1)估算振型分解反应谱分析下速度相关型阻尼器的附加有效阻尼比。由于振型分解反应谱分析属于静力分析，分析结果虽包含结构的预期位移，但并不体现结构质点的运动模式，从而以上几个前提并不完全成立。消能减震结构在进行振型分解反应谱法分析时，若套用式(1)来计算黏滞阻尼器的附加有效阻尼比，则自然隐含了一个假定：黏滞阻尼器是在振型分解反应谱分析得到的预期变形下按第一周期进行简谐运动。因此，严格来说，采用式(1)得到结构的附加有效阻尼比为黏滞阻尼器在该运动模式下所提供的阻尼比。然而黏滞阻尼器在实际地震作用下并非按照该模式运动，此方法虽然被普遍采用，但具有局限性，并不具备明确的物理意义。

采用式(1)估算阻尼器的附加有效阻尼比时，对于位移相关型阻尼器，阻尼力仅与变形有关，可通过与结构预期位移对应的阻尼器变形来确定其所消耗的能量，并通过迭代来确定附加有效阻尼比[10-12]，因此可采用振型分解反应谱法分析。但对于速度相关型阻尼器，阻尼力与变形速度有关，无法仅由与结构预期位移对应的阻尼器变形来确定其所消耗的能量，还必须假定结构按第一周期进行简谐运动，才能确定阻尼器所消耗的能量。所以，对于非线性速度相关型阻尼器，在进行迭代时，常无法收敛，难以获得其附加有效阻尼比。

由于无法由振型分解反应谱分析来计算黏滞阻尼器在结构中的附加有效阻尼比，实际工程通常采用由时程分析得到的黏滞阻尼器所做的功与结构的总应变能来计算黏滞阻尼器的附加有效阻尼比[13]，并将该阻尼比返回振型分解反应谱分析来进行结构设计。常用的时程分析下黏滞阻尼器附加有效阻尼比计算公式如式(2)或式(3)

(2)

(3)

式中：Ek,max与Ep,max分别为结构在时程过程中的最大动能与最大势能；WA与WM分别为阻尼器与振型阻尼在时程过程中累计消耗的能量；Ei为时程过程中累计输入的总能量。

②教师地位的转变。“互联网+”时代的来临，学生的获取方式与传播方式都发生了革命性的转变，“不懂问百度”以成为学生的口头禅，学生通过网络可轻松获得答案，教师的地位也逐渐由权威转变为参考。网络公开课目前呈现爆炸式发展趋势，学生在网上就能与名师名校的距离拉近，在知识的获取中，语文老师的权威地位受到挑战而变得日益下降，“传统课堂-满堂灌”的传播方式已经不能满足知识日益增长的获取方式。

然而，采用式(2)或式(3)的出发点其实是为了套用式(1)，但并不具备物理意义，原因在于：WA,WM,Ei均为整个时程过程的能量累积，Ek,max与Ep,max均为整个时程过程的最大值，并非发生在同一时刻。因此，采用此二式计算时程分析中阻尼器的附加有效阻尼比是不合理且不可靠的，若将该附加有效阻尼比返回振型分解反应谱分析来进行结构设计是不安全的。为了有效计算黏滞阻尼器在结构中提供的附加阻尼比，本文从能量角度出发，由结构运动方程重新推导附加有效阻尼比的理论解。

2 附加有效阻尼比的理论解

对于不含阻尼器的单自由度结构，运动方程为

(4)

(5)

式中：cd为黏滞阻尼器的阻尼系数;α为阻尼指数。当α=1时，阻尼器为线性黏滞阻尼器，其附加有效阻尼比可套用固有阻尼比的计算公式来获得，即：ξa=cd/(2mωn)；当α≠1时，阻尼器为非线性黏滞阻尼器，其附加有效阻尼比则无法套用固有阻尼比的计算公式来获得。

为此，可将非线性黏滞阻尼器等效为线性黏滞阻尼器，若是基于阻尼力的等效，即：两者在时程过程中任一时刻t的阻尼力Fd相等，则有

(6)

若是基于能量的等效，即：两者在同一时程过程(0,t)中所消耗的能量WA相等，则有

(7)

(8)

从而可得黏滞阻尼器的附加有效阻尼比ξa为

(9)

(10)

特别地，当质点按自振周期做简谐运动时，可假设质点位移u(t)为

u(t)=u0sin(ωnt)

(11)

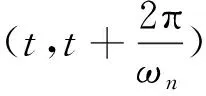
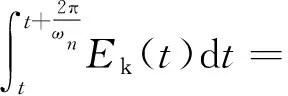
(12)

(13)

将式(13)代入式(9)，可得附加有效阻尼比ξa

(14)

此时，式(9)则退化为式(1)。对比式(1)与式(9)可见，虽然附加有效阻尼比ξa与质点动能Ek(t)在时间上的积分有关，但当质点按自振周期做简谐运动时，质点动能在时间上的积分可用结构应变能来表示，因此，式(1)仅适用于计算质点按自振周期做简谐运动时的附加有效阻尼比，式(9)则适用于计算任意动力荷载下的附加有效阻尼比，具有更强的适用性和合理性。

(15)

同理，振型阻尼比ξm可表示为

(16)

当时间间隔Δt越小，上式计算的阻尼比越接近真实解。

3 有限元分析验证

现采用ETABS软件并以一单自由度体系为例，分别验证振型阻尼比ξm与附加有效阻尼比ξa的计算公式。该单自由度体系采用单层单跨混凝土框架结构，如图1所示。结构跨度为6 m，高度为3 m，混凝土材料为C30，框架柱截面尺寸为400 mm×400 mm，框架梁截面尺寸为200 mm×400 mm，楼板厚度为100 mm。楼面永久荷载(含楼板自重)为4 kN/m2，楼面活荷载为2 kN/m2。在该结构中布置黏滞阻尼器，如图2所示，阻尼器阻尼系数cd=200 N/(m/s)α，α分别取值0.1，0.2，0.3，结构振型阻尼比ξm采用0.05。地震波分别采用正弦波(周期1 s，持续时间30 s)、三角波(周期1 s，持续时间30 s)、El-Centro波(持续时间53.76 s)，ChiChi波(持续时间40 s)，进行时程分析时将结构的活动自由度限制在X-Z平面内，并将楼板设置为刚性楼板，以确保结构为单自由度。

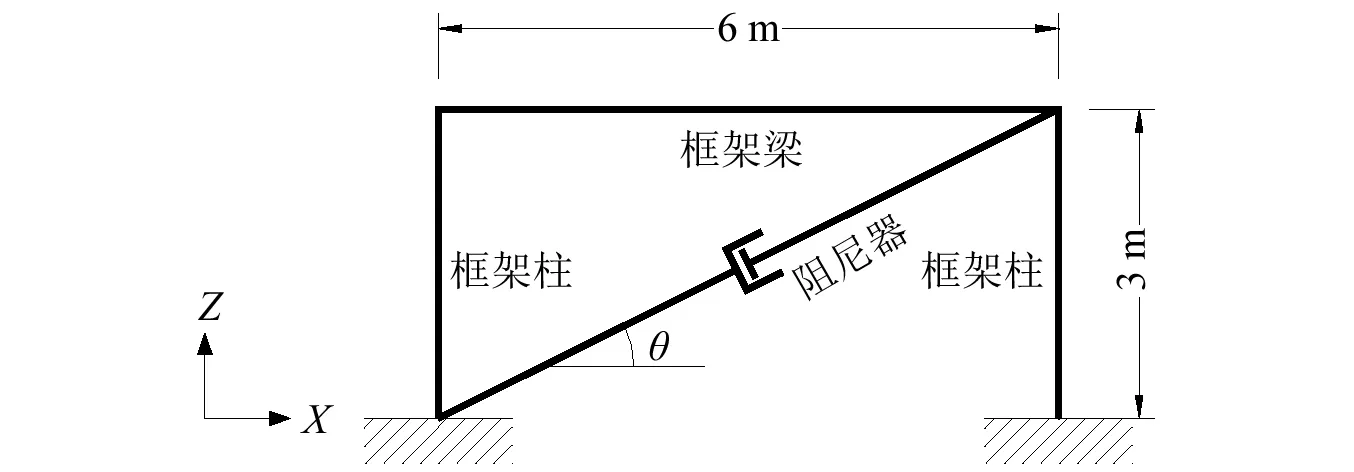
图2 单层单跨混凝土框架结构(设置阻尼器)Fig.2 1-floor 1-bay concrete frame structure-with damper

先将时程分析结果采用式(16)计算所得的振型阻尼比ξm如表1所示。由表1可知，采用式(16)计算所得振型阻尼比ξm与已知的输入值5.00%完全一致，证明了该计算方法的正确性，并适用于任意形式的地震波。

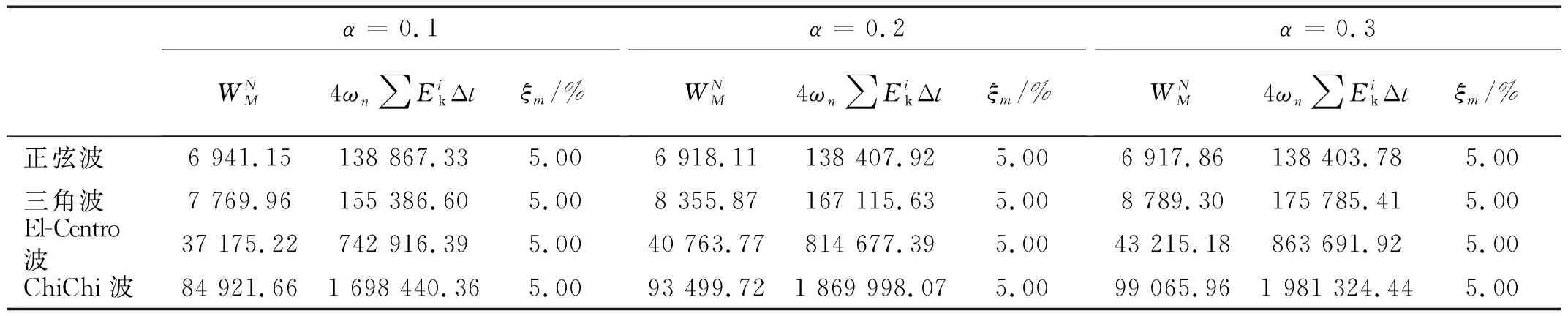
表1 振型阻尼比计算值Tab.1 Calculated values of modal damping ratio

再将α=0.2(α=0.1，α=0.3的情况不再列举)对应的时程分析结果分别采用式(2)与式(3)计算所得的振型阻尼比ξm如表2所示。由表2可知，采用式(2)与式(3)计算所得振型阻尼比ξm均与已知的输入值5.00%差别较大，由此可认为采用式(2)或式(3)计算黏滞阻尼器的附加有效阻尼比ξa是不合适的。

表2 振型阻尼比计算值——采用式(2)与式(3)计算Tab.2 Calculated values of modal damping ratio——using equations (2) and (3)

然后，将时程分析结果采用式(15)计算所得的附加有效阻尼比ξa分别如表3所示。由表3可知，与振型阻尼比ξm的不同在于，非线性黏滞阻尼器的附加有效阻尼比ξa在不同的时程过程是不同的。

表3 附加有效阻尼比计算值Tab.3 Calculated values of additional effective damping ratio

此外，将表3中的α=0.2(α=0.1,α=0.3的情况不再列举)对应的附加有效阻尼比ξa叠加到不设置阻尼器结构(图1)的振型阻尼比ξm后，进行时程分析，所得的不设置阻尼器模型阻尼能WM与带阻尼器模型阻尼能WM+WA如表4所示。由表4可知，在同一时程过程中，设置阻尼器结构的振型阻尼与阻尼器所做的功之和WM+WA，与振型阻尼在振型阻尼比为ξm+ξa的不设置阻尼器结构中所做的功WM是相等的(误差来自有限元程序的计算精度)。因此，式(15)计算的阻尼比可视为该时程过程的附加有效阻尼比，这种等效是基于阻尼能的等效。

表4 阻尼能对比Tab.4 Comparison of damping energies

最后，对比式(9)与式(10)可得，当振型阻尼比ξm为已知时，可直接通过黏滞阻尼器与振型阻尼所做的功的关系来确定附加有效阻尼比ξa，即

(17)

虽然式(17)是建立在单自由度结构的前提下推导出的，但也同样适用于多自由度结构。将时程分析结果采用上式计算所得的附加有效阻尼比ξa如表5所示，可以看出，采用上式计算所得的附加有效阻尼比与采用式(16)计算结果完全一致，因此，当结构振型阻尼比ξm已知时，采用式(17)确定附加有效阻尼比更加便利。

表5 附加有效阻尼比计算值Tab.5 Calculated values of additional effective damping ratio

4 结 论

(1)现有的消能减震结构附加有效阻尼比计算公式(1)是由单自由度质点固有阻尼比的原始定义推导出的，假设质点按自振周期做简谐运动，并以能量的形式来表达的。因此，该公式具有局限性，不适合用于计算消能减震结构在时程分析中黏滞阻尼器的附加有效阻尼比。

(2)实际工程中常用的消能减震结构在时程分析中黏滞阻尼器的附加有效阻尼比的计算式(2)与式(3)不具备物理意义，所计算的附加有效阻尼比是不合理且不可靠的。

(3)本文基于能量的等效，将非线性黏滞阻尼器等效为线性黏滞阻尼器，提出黏滞阻尼器的附加有效阻尼比计算公式，该公式经由已知的结构振型阻尼比验证了其正确性，适用于计算任意动力荷载下的附加有效阻尼比，具有更强的适用性和合理性。

(4)本文提出的计算公式所计算的非线性黏滞阻尼器的附加有效阻尼比在不同的时程过程是不同的。

(5)将本文提出的计算公式所计算的附加有效阻尼比叠加到不设置阻尼器结构的振型阻尼比后，其振型阻尼做所的功，与消能减震结构在同一时程过程下的振型阻尼与阻尼器所做的功之和相等，因此，本文提出的计算公式所计算的附加有效阻尼是基于阻尼能的等效。

(6)当振型阻尼比为已知时，可直接通过黏滞阻尼器与振型阻尼所做的功的比值关系来更加便利地确定附加有效阻尼比。