CFD数值模拟船舶在波浪中的回转操纵运动

王建华 ，万德成

1上海交通大学海洋工程国家重点实验室，上海200240

2高新船舶与深海开发装备协同创新中心，上海200240

3上海交通大学船舶海洋与建筑工程学院，上海200240

0 引 言

船舶操纵运动可以反映出船舶在航行过程中的机动性、回转特性和航向的纠偏能力。操纵性能的优劣与船舶的航行安全和能耗息息相关，其重要性不言而喻。目前，船舶的操纵性能评估主要通过典型的操纵运动试验进行，其中对船舶自由回转操纵运动的数值模拟是评估船舶回转性能的重要手段。船舶自由回转操纵运动一般通过执行目标舵角，使船舶在舵提供的回转力和力矩作用下实现回转运动，典型的自由回转操纵运动轨迹及特征参数如图1所示。一般在船舶设计的初期阶段，就需要评估所设计船舶的操纵运动特性，尤其是回转特性，以指导船舶航行中的操作，保障船舶全寿期的安全性能。

图1 船舶自由回转操纵运动轨迹及特征参数［1］Fig.1 Free turning maneuvering motion trajectory and main parameters of ship［1］

一般船舶操纵都是通过后舵操作，实现特定的操纵运动。因此，为了精确地评估船舶操纵运动特性，需要考虑到船—桨—舵的相互耦合作用。目前，应用较为广泛的船舶操纵性预报方法主要有船模试验方法和基于CFD的数值模拟方法。船模试验方法是目前应用最广泛也是最可靠的方法，尤其是近年来得益于试验装置和方法的改进，使得自航船模的操纵试验成为了可能。该方法可以通过在海洋工程波浪水池中或者天然湖泊中开展特定的操纵运动试验，来预报船舶操纵性能。但该方法需要较大的试验水池、精确的螺旋桨和舵控制系统以及用于测量船体六自由度运动的设备。此外，为真实还原船舶操纵运动中的实际流场，需要有与实际环境相似的试验水池，故船模试验方法的设备和试验成本高。而且，鉴于当前的流场测量设备（如粒子图像测速（PIV）等）普及性及适用性有限，试验中尚给不出操纵运动过程中船体、螺旋桨和舵周围精细的流场结构，并无法详细分析在此过程中船舶的水动力性能变化。

基于CFD的操纵运动数值模拟研究可分为约束船模操纵运动和自航船模操纵运动。前者通过结合操纵运动数学模型，依据数值模拟约束船模操纵运动得到各个水动力导数，进而对典型的船舶操纵性能进行仿真，其被广泛应用于船舶操纵运动的数值模拟。Simonsen等［2］利用自主开发的求解器CFDShip-Iowa，数值模拟了静态和动态平面运动机构（PMM）试验，并且分别采用CFD计算和试验测量得到的水动力导数，根据分离型操纵性数学模型，对标准集装箱（KCS）船模在静水中的回转操纵和Z形操纵试验进行模拟。Guo和Zou［3］采用商业软件 STAR CCM+数值模拟了标准船模ONRT的旋转试验、静态斜拖试验和纯横摇试验的操纵运动，数值回归得到了操纵性水动力导数值，运用四自由度的操纵运动数学模型（MMG）仿真了船舶25°自由回转和20/20 Z形操纵运动，预报的运动轨迹与试验值吻合较好，验证了采用CFD方法数值模拟约束船模操纵运动试验得到的操纵性导数值的可靠性。通过数值构建船—桨—舵整体耦合运动求解模型，进行自航船舶操纵运动的直接数值模拟，可以更精确地描述船舶操纵运动过程。

目前，随着高性能计算机的快速发展以及重叠网格技术的逐步完善，直接数值模拟自航船模的操纵运动已成为现实。Carrica等［4］采用自主开发的水动力学软件CFDShip-Iowa V4，模拟了不同航速下（Fr=0.25，0.41）船舶自由回转（35°舵角）和Z形操纵（20/20）特性，在数值计算中，利用动态重叠网格技术处理大幅度的船舶操纵运动，并对波浪工况下的特性进行计算，其数值预报的操纵性参数与试验值的误差在10%以内，指出简化的螺旋桨体积力模型是预报误差产生的主要原因，该模型忽略了真实情况下螺旋桨旋转导致的对船体运动的阻力及其受到的侧向力影响等因素。Mofidi和 Carrica［5］采用同样的求解器，但是考虑了真实情况下旋转的螺旋桨，进行了典型10/10 Z形操纵试验和修正型的15/1 Z形操纵试验的数值模拟，数值预报的船体运动及操纵性参数与试验结果吻合良好，并且对自航操纵运动过程中的详细流场进行了分析。Broglia等［6］和 Dubbioso等［7］分别进行了单舵及双舵情况下双桨推进船舶的自由回转试验数值模拟，其中舵和船体运动采用动态重叠网格进行处理，将得到的船体运动轨迹与试验结果进行对比，并比较了单舵和双舵情况下自由回转运动轨迹和回转降速、漂角及横摇等时历曲线，分析了回转运动全过程中的舵力和船体、附体的侧向力变化，指出在双桨情况下舵会强烈干扰螺旋桨受到的载荷。Shen等［8］基于开源CFD计算平台OpenFOAM，开发了船舶水动力学求解器 naoe-FOAM-SJTU［9-11］，引入了重叠网格模块，并扩展到船—桨—舵相互作用下的船舶自航［12］和操纵运动［13-15］模拟计算中，验证了采用非结构化网格直接进行带螺旋桨、带舵船舶的操纵运动数值模拟的可行性。

综上所述，虽然结合重叠网格技术的CFD方法已经广泛应用于船舶操纵运动的直接数值模拟，但是大部分研究都是针对静水工况下的操纵运动，而海上航行的船舶经常处于波浪环境中，因此很有必要开展波浪工况下操纵运动的精确预报，为船舶设计提供更为精确的数据支撑。本文将采用结合重叠网格技术的CFD求解器naoe-FOAM-SJTU，直接数值模拟带螺旋桨、带舵船舶在波浪中的自由回转操纵运动，预报船舶在波浪中的操纵运动特性。通过数值计算船、桨、舵周围精细的流场，分析船舶在自由回转过程中的水动力变化和船、桨、舵干扰以及波浪对船舶回转性能的影响。

1 数值计算方法

1.1 流体计算控制方程

本文计算域流场求解的控制方程为非定常两相不可压缩的RANS方程：

式中：▽为求散度；U为速度场；pd=p-ρg·x，为动压力，其数值等于总压力值减去静水压力；ρ为液体或者气体的密度；x为空间坐标；t为时间；g为重力加速度向量；μeff=ρ(ν+νt)为有效动力粘性，其中v为运动粘度，vt为涡粘度;fσ为表面张力项。

湍流模型采用SSTk-ω［16］，该模型兼具标准k-ω和k-ε模型的优点，能够保证壁面处和远流场求解的精确性和可靠性。自由面求解采用带有人工可压缩项的VOF（Volume of Fluid）方法［17］，两相VOF输运方程定义为

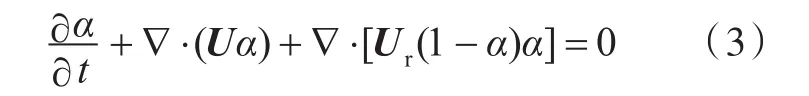
式中：Ur为用于压缩界面的速度场；α为两相流体的体积分数，代表液体部分所占体积的百分比，取值范围为0～1，0表示气体，1表示水，介于0到1之间则表征为自由面位置。因此，通过体积分数α便可以将两相流规化为统一的流体域。

上述RANS方程（式（1）～式（2）），VOF输运方程（式（3））和湍流方程都采用有限体积法来进行离散。采用OpenFOAM自带的离散格式进行方程离散，时间项采用隐式Euler格式，对流项采用二阶TVD格式，耗散项采用中心差分格式，VOF方程中对流项采用Van Leer格式离散。流体控制方程求解中，速度压力解耦采用PISO算法［18］。

1.2 自航船舶操纵运动控制模块

船舶操纵一般都会有大幅度的船舶运动，传统的变形网格在模拟物体大幅度运动时网格质量会下降，影响求解精度；而重叠网格技术允许多个相互独立的网格之间产生无约束的相对位移，在计算过程中能够保证网格不发生变形，从而保证计算过程中网格的质量，因此非常适用于带桨、带舵船舶操纵运动问题的数值求解。采用动态重叠网格技术离散的船、桨、舵多级物体运动模型如图2所示。螺旋桨和舵根据不同船体运动形式，可以按照指定的控制参数（如螺旋桨转速、最大转舵角度等），绕着旋转轴进行自身的旋转运动，船体则在桨、舵自身运动以及船体受力情况下在自由面环境下做六自由度的运动。

图2 船—桨—舵多级物体运动示意图Fig.2 Diagram of motions in ship-propeller-rudder system

依托重叠网格方法以及多级物体运动模块，可以很方便地实现自航船舶的操纵运动控制，即通过对舵角的控制，实现特定船舶操纵运动的数值模拟。35°满舵向右舷进行自由回转操纵运动的舵角控制方程为

式中：δ(t)为舵角；k为转舵速率；tp表征进行回舵的时刻，从而结束回转运动，即何时回到初始零度舵角。在起始时刻，按照转舵速率k进行转舵直到满舵状态，之后维持此舵角完成回转操纵运动，根据模拟需求进行回舵操作，结束回转运动。

1.3 区域造波方法

区域造波方法与速度入口边界造波方法直接的区别就是前者不仅需要边界造波，同时还需要在特定的区域范围内对流场进行改造。具体实现方式是通过采用松弛区域，保证外部边界处没有波浪反射，同时还能够确保计算域内部的波浪反射不会对造波边界产生干扰，这也是边界造波方法所不具备的特点。本文采用开源造波工具包waves2Foam［19］在移动计算域中进行波浪场生成。采用环形造波区，如图3所示，进行回转操纵运动过程中的波浪生成，环形区域中通过松弛方式即可实现造波，同时也能完成消波。该造波区在计算中可以跟随计算域进行移动，因此可以保证波浪在船舶进行360°回转运动过程中可以传播到整个计算域中。图中，L为船长。

图3 区域造波图示Fig.3 Diagram of wave generation zone

2 计算模型和工况

本文计算船型采用全附体双桨、双舵的ONRT船模，该船模是被广泛应用于CFD验证的标准船型，被列为Tokyo2015 CFD研讨会上的自航模问题的标准船型。对于该船型，有非常丰富的操纵试验数据，从而可以验证当前数值预报手段的可靠性。船体的几何模型如图4所示。船体的主尺度如表1所示。

图4 ONRT船几何模型Fig.4 Geometry model of ONR Tumblehome ship

表1 ONRT船体模型主尺度Table 1 Main particulars of ONR Tumblehome ship model

数值计算中采用重叠网格方法进行船、桨、舵网格的直接划分，重叠网格的布置如图5所示。计算域共分为6部分，即背景网格、船体周围网格、2套螺旋桨网格和2套舵的网格，划分完成的网格如图6所示，计算网格总数量为711万。

图5 重叠网格布置Fig.5 Overset grid arrangement

图6 桨和舵周围网格分布Fig.6 Local grid distribution around twin propellers and rudders

本文进行了在35°舵角下，船舶在波浪中的自由回转操纵运动的直接数值模拟，船舶初始航速为1.11 m/s，对应于Fr=0.2，数值计算中螺旋桨的转速设置为对应于这个航速下的模型自航点值，为 529.14 r/min［13］。入射波浪根据 IIHR 的试验［20］进行设置，入射波浪的波长λ等于船长LWL，波陡H λ为 0.02。

3 波浪中船舶自由回转数值模拟结果分析

波浪中的自由回转操纵运动数值模拟从最终稳定的自航数值计算开始，然后开始放开船舶的六自由度运动，与试验的一致，均在入射波浪的波峰到达船艏时进行操舵，舵按照自由回转操纵运动进行控制。所有数值计算均在上海交通大学船海计算水动力学研究中心高性能计算集群进行，采用40个进程并行计算，计算时间步长为Δt=0.000 5 s，对应于每个时间步螺旋桨转过1.5°。完成波浪中的自由回转操纵运动共耗时1 206 h，对应于155 000个时间步。

图7所示为数值预报的波浪中船舶自由回转得到的运动轨迹以及与试验值［17］的对比。从图中可以看出，当前的数值预报结果与试验结果吻合较好，但是数值预报的回转圈会比试验的结果更大，这主要是由于数值计算中为了保证重叠网格间足够的插值单元，而对舵的几何模型进行了修正，减小了有效的舵面积，因此使得舵效减小。此外，从图中还可以看出，在船舶航向角改变90°和270°时，回转曲线会产生明显的波动现象。图8所示为对应的局部放大对比图，在对应的2个时间段，船舶的运动轨迹会产生明显波动，并且试验和CFD预报结果都显示有这一现象。数值计算得到的波动幅值明显小于试验中的波动值，这也说明了CFD模拟中船舶的回转性较试验稍差，这也解释了图7中数值预报的船舶回转圈更大的原因。

图7 回转圈轨迹对比Fig.7 Comparison of turning circle trajectory

图8 局部回转运动对比Fig.8 Local comparison of trajectory

数值预报的船舶回转圈特征参数及其与试验值［20］的对比如表2所示。

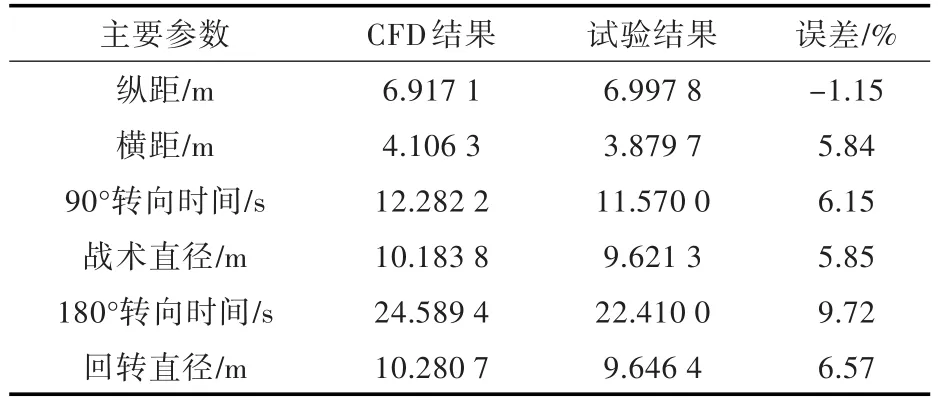
表2 回转圈轨迹特征参数对比Table 2 Comparison of main parameters of turning circle trajectory

仿真过程中，为了保证对比的可靠性，对时间尺度进行了调整，使得CFD模拟和物理试验满足在同一个时刻执行转舵操作。从表中的对比结果可以看出，所有特征参数与试验值的误差均在10%以内，当前的数值计算可以较高的精度预报出波浪中自由回转船舶的操纵运动特性。

图9所示为数值预报船舶在波浪中自由回转过程中六自由度运动的时历曲线。从图中可以看出，船舶的垂荡、纵摇和横摇运动会产生较为明显的波频振荡特性（图9（a），（b）（c））。另外，由于回转运动过程中船舶遭遇的浪向角也在时刻变化，因此在高频的波频运动下还存在由于回转操纵运动导致的低频波动。整个回转运动过程中，最大的纵摇幅值可达2.5°，横摇运动的幅度为-4.4°～8°。此外，从横摇运动的时历曲线（图9（c））可以看出，由于波浪导致的横摇运动幅值较由于初始操舵导致的横摇运动更大。而3个平面的运动，纵荡、横荡和艏摇运动则展现较小的波频运动特性。从艏摇运动的曲线（图9（d））上可以看出较小的波动，这也可能导致了图8中展现的平面运动轨迹中的局部波动。

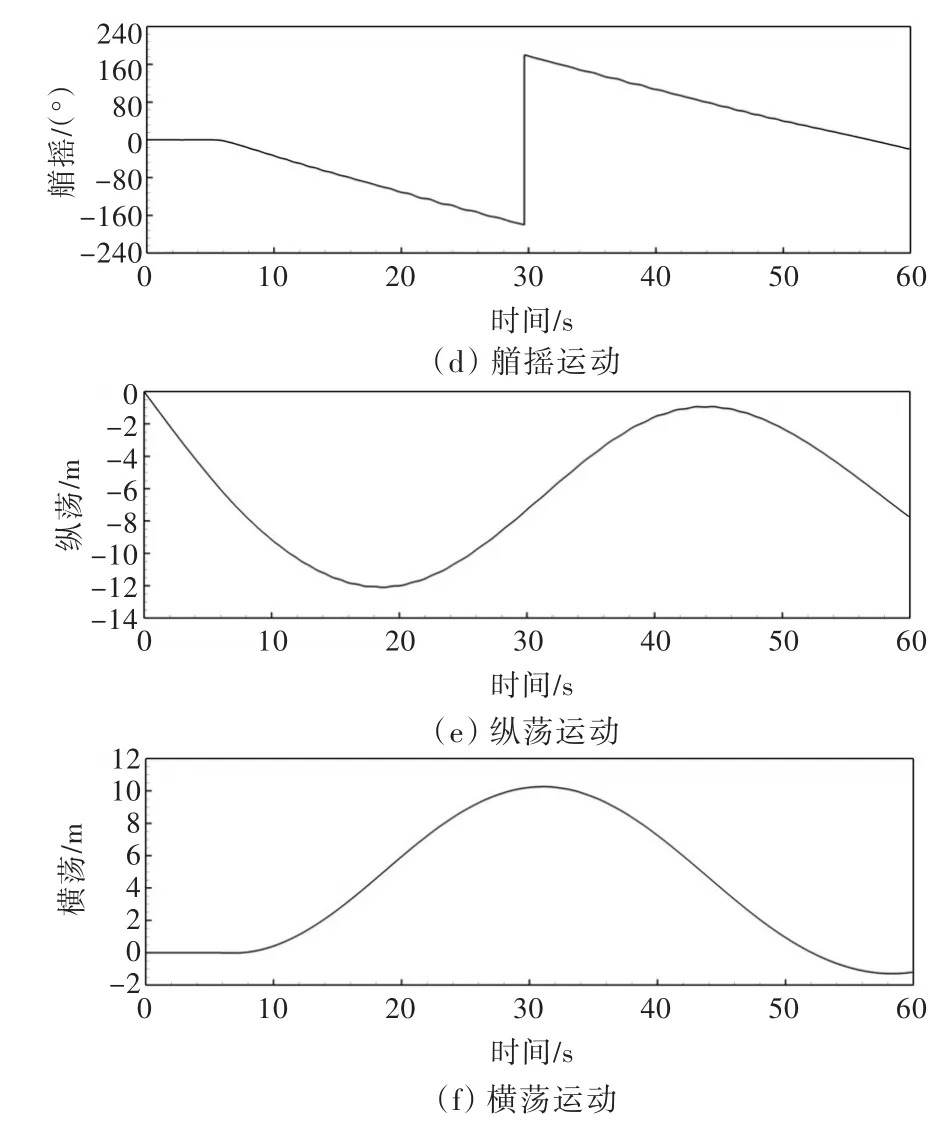
图9 波浪中自由回转操纵中船舶六自由度运动时历曲线Fig.9 Time history curves of ship motions for turning circle maneuvering in waves

图10所示为船舶在波浪中自由回转运动过程中的航速以及艏摇速率的变化曲线。从图中可以看出，波浪中的船舶在回转运动过程中会出现明显的回转降速现象，并且最大降速可达40%。初始的航速降低是由于转舵导致的，进入回转运动以后会维持在平均30%的降速范围内。而对于艏摇速率来说，初始的明显速率变化是由于受到转舵的影响，而后期的波动则是由于船舶遭遇变化的浪向导致，最大的艏摇速率可达12.2（°）/s。

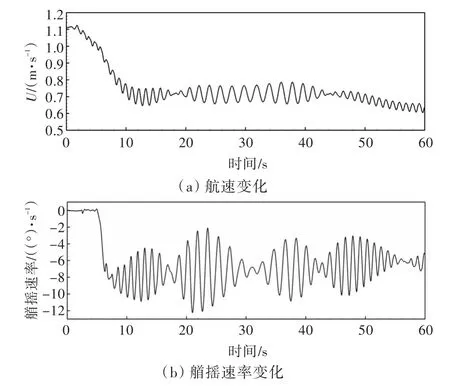
图10 波浪中自由回转操纵中船舶航速和首摇速率时历曲线Fig.10 Time history curves of ship speed and yaw rate for turning circle maneuvering in waves

图11所示为船舶在波浪中进行自由回转操纵运动过程中螺旋桨推力和扭矩的变化曲线。从图中可以看出，螺旋桨的推力和扭矩呈现出明显的波频振动特性，这主要是由于船舶运动过程中导致螺旋桨的进流产生变化，进而使得推进性能产生波动。从局部放大图中可以看到更为高频的振荡现象，这是由于真实旋转螺旋桨叶片切割流场导致。

图11 波浪中自由回转操纵中船舶推进性能时历曲线Fig.11 Time history curves of propulsion coefficients for turning circle maneuvering in waves

图12所示为转舵时刻舵所受到的水动力载荷的变化曲线。从图中可以看出，执行转舵操作之前，作用在两侧舵上的阻力基本一致，并且侧向力对称，而执行完操舵以后，舵阻力增加明显，而侧向力变成同向，产生较大的侧向合力，而侧向力的合力也使得船舶产生回转运动。

图12 转舵过程中舵受到的水动力时历曲线Fig.12 Time history curves of rudder forces during rudder execution

图13所示为在转舵过程中的桨舵周围的涡量场变化。从图可以看出，初始时刻，舵角为0°时，桨舵周围的涡量分布基本为对称形式，而随着舵角的增加，舵对前面螺旋桨的泻涡会产生明显的干扰，由于舵向左舷转动，因此左舷舵会对螺旋桨的桨毂涡产生干扰，而右舷舵则会影响到右舷桨的叶梢涡。这种现象的区别也解释了图11和图12中两侧螺旋桨和舵水动力的区别。而舵周围会发生明显的流动分离现象，但是现在采用的是RANS方法，无法精确地捕捉这种情况下的周围流动，因此会对舵力的计算产生误差，这也是导致目前计算中的回转圈变大的原因之一。

图13 转舵过程中桨舵周围的涡量场Fig.13 Snapshots of vortical field around twin propellers and rudders during rudder execution

图14所示为船舶在波浪中自由回转过程中，4个典型时刻的自由面波形变化，分别对应于0°、120°、240°和 360°航向角的时刻。从图中可以看出，在没有转向时，船舶周围的波浪环境基本对称，但是在回转角度达到360°时，船艏和船艉处均能看出由于转动导致的两侧波面的差别；而从120°和240°航向角时的自由面可以看出，两侧波面存在明显的高度差别，这也导致了船体两侧的压力分布不均；从图14（d）同样可以看出船艏会抬出水面，这证明了在该波浪情况下船舶会产生大幅度的六自由度运动。

图14 波浪中自由回转过程中船舶周围自由面Fig.14 Snapshots of wave elevation around ship hull for turning circle maneuvering in waves

4 结 语

本文采用结合重叠网格技术的CFD求解器naoe-FOAM-SJTU，对船—桨—舵相互作用下的波浪中船舶自由回转操纵运动进行了直接数值模拟。数值预报的波浪中船舶回转运动的回转圈特征参数（如纵距、横距、战术直径、回转直径等）与已有试验结果吻合较好，误差均在10%以内，验证了当前求解器对船—桨—舵相互作用下的波浪中船舶自由回转操纵运动预报的适用性和可靠性。此外，根据计算结果显示，船舶的垂荡、纵摇和横摇运动展现出明显的波频运动响应，而纵荡、横荡和艏摇3个平面运动的波频振动特征不明显。在波浪中船舶进行自由回转时的最大船舶失速可达40%。同时，给出了整个操纵运动过程中的推进性能和舵力的变化。并且通过详细的流场信息，如不同时刻自由面变化和桨、舵周围涡量场变化等，分析了波浪中回转操纵运动下水动力变化的原因。

由于当前数值模拟采用时均的RANS方法进行流场求解，因此对于桨、舵周围大分离流动现象捕捉的精度较差，这也导致了目前的数值预报存在一定的误差，将来的工作将主要开展基于更为精确的分离涡模拟方法进行该问题的求解，以给出更精细的流场模拟，获取更高精度的数值预报结果。