滑行艇阻力计算方法对比研究

孙源，卢晓平，李井煜，王中

海军工程大学舰船与海洋学院，湖北武汉430033

0 引 言

滑行艇，是指在高速下全艇的重量大部分由水动升力支持的船艇，亦即实现了动力航行的船艇，其优良的高速特性使之得到了广泛的关注和应用。基于该型艇特殊的性能和速度要求，高速滑行艇的设计及性能分析过程十分重要，因而建立快速、准确的滑行艇阻力计算方法具有重要意义。经过数十年的研究和发展，滑行艇阻力计算研究取得了许多有意义的成果，同时也还存在着不少尚需解决的问题。现有的滑行艇阻力计算方法可分为2大类：半经验半理论方法和数值计算方法。其中，半经验半理论方法主要包括［1］：

1）利用现有艇的统计资料进行估算；

2）查洁法［2-3］。继前苏联中央流体动力中心之后，我国舰船设计单位也开始使用该方法对滑行艇阻力进行计算；

3）SIT法［4］。该方法是根据美国Stevens实验室水池试验结果而提出，普遍应用于欧美等国；

4）舒福德—勃朗法。该方法由 Shuford［5］根据“横流理论”提出，然后，Brown［6］通过大量实验对其原始公式进行了改进。

数值计算方法作为一种新兴而有效的工具，已经可以对排水型船舶阻力进行较为准确的预报。但在滑行艇阻力预报方面，国内外有关CFD水动力计算及其工程运用的相关研究仍然较少。Yousefi等［7］针对近年来在高速滑行艇水动力方面的研究进行了总结，并对比了多种商用CFD软件的主要特点。曹洪建［8］使用FLUENT软件，对滑行艇于静水中的直航运动进行了数值模拟，证明采用该软件计算滑行艇阻力性能具有一定的准确性。魏子凡等［9］基于NUMECA系列软件，对多种滑行艇进行了数值计算及阻力分析，并以此为依据对滑行艇附属装置进行了优化。常亮等［10］采用运动域方法对滑行艇流场进行了数值模拟，经试验验证，表明该方法具有较好的准确性。孙华伟等［11］运用STAR CCM+软件探讨了结构网格因素对滑行艇阻力计算精度的影响。王硕等［12］同样基于STAR CCM+软件，采用切割六面体网格对滑行楔形体和滑行艇进行了阻力预报，所得结果的精度能够满足工程应用要求。

本文将分别使用半理论半经验方法以及基于STAR CCM+软件的数值计算方法对滑行艇模型阻力开展计算，并采用试验所得数据进行对比和验证，证明半理论半经验方法及CFD数值计算方法在解决滑行艇滑行状态下的阻力计算方面具有可靠性，用以为后续多体滑行艇阻力计算打下基础。

1 艇型参数及计算方法

1.1 艇型建立

本文所研究的滑行艇艇型是在确定主尺度的前提下，依据美国62系列滑行艇的船型资料确定船型函数，然后再结合仿射变换法和船型函数变换法得到具体的艇型。其横剖线图及三维构型图如图1所示，根据该艇型制作的1/10比例模型参数如表1所示。

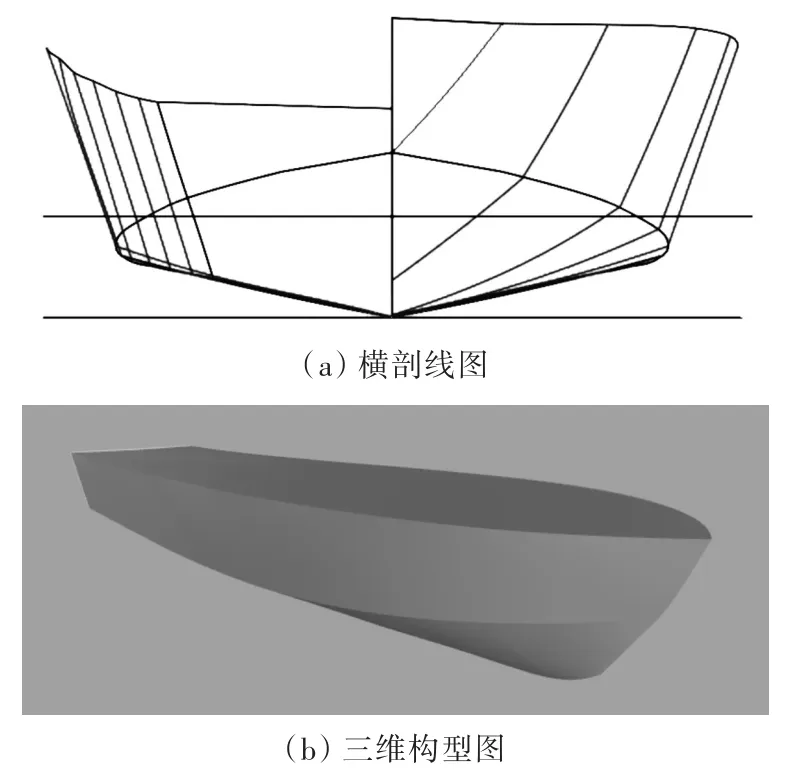
图1 滑行艇线型图Fig.1 Profile of the planing craft

表1 模型参数Table 1 Model parameters

1.2 半理论半经验方法

常用的半理论半经验方法包括查洁法、SIT法和舒福德—勃朗法等，这类方法均是以基本的理论公式为基础，再结合大量的试验数据进行经验系数的修正，从而得到既能反映物理实质，又能针对因物理模型过分简化而引起的误差进行补偿的一类计算方法。这些方法被广泛应用于各国滑行艇的阻力计算之中。其中，查洁法已在我国船舶设计单位中得到使用；SIT法作为姆雷法的修正及补充，也多见于滑行艇阻力计算研究中；而舒福德—勃朗法从原理上讲较前两种方法更为合理，但由于其计算较为复杂，并未得到广泛应用。

1.2.1 查洁法

采用查洁法计算滑行艇阻力的具体步骤如下：

1）已知艇重Δ，航速V，艇宽B（舯部折角线宽度和艉部折角线宽度的平均值），重心至艉板的水平距离ξg，计算艇宽傅汝德数，升力系数（其中ρ为流体密度），重心纵向位置系数mΔ=ξg/B。

2）求解方程组（1），得到纵倾角α和浸湿长宽比λ。

3）对纵倾角α进行计及斜升角β影响的修正。

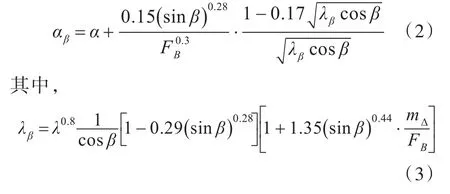
4）计算浸湿面积S=λB2、浸湿长度I=λB以及雷诺数Rn=V·I/ν，其中ν为运动粘性系数。5）计算总阻力：

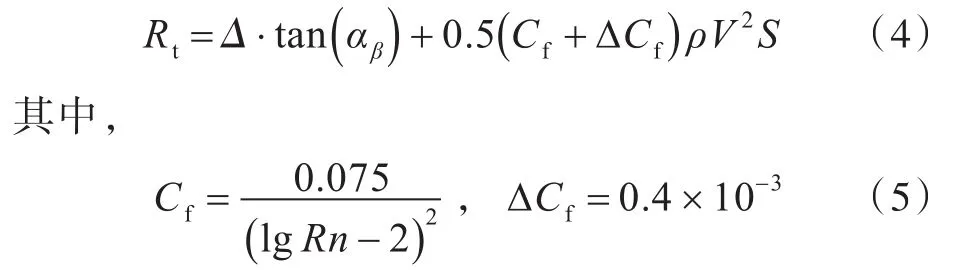
式中，Cf为摩擦阻力系数。

1.2.2 舒福德—勃朗法

采用舒福德—勃朗法计算滑行艇阻力的具体步骤如下：

1）已知艇重Δ，航速V，艇宽B，重心至艉板的水平距离ξg，计算艇宽傅氏数和升力系数

2）求解方程组（6），得到纵倾角α及浸湿长宽比λ。

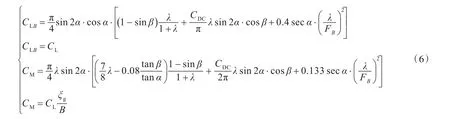
式中：CLB为计及勃朗修正的以船宽B为特征尺度的升力系数；CM为力矩系数；CDC为横流阻力系数，考虑艇型实际情况，取CDC=4/3。

3）计算浸湿面积S=λB2/cosβ、浸湿长度I=λB和雷诺数Rn=V·I/ν。

4）计算总阻力：

1.3 CFD数值计算方法

STAR CCM+是一款新型的CFD计算软件，其功能包含了从几何模型的建立、表面网格的准备、体网格的划分、模型的设定、计算求解，一直到后处理分析的整个模拟过程，被广泛应用于船舶水动力性能计算和模拟中，并取得了显著成果。与以往采用重叠网格的方法不同，本文采用STAR CCM+软件中的DFBI模块对滑行艇模型阻力进行数值计算。该方法在计算排水型船舶阻力结果方面精度较高，但针对高速滑行状态下的阻力计算，资料仍然较少。

1.3.1 控制方程

采用雷诺平均法进行数值求解。在笛卡尔坐标系下，张量指标形式下的时均连续方程和动量方程（Navier-Stokes方程）如下：

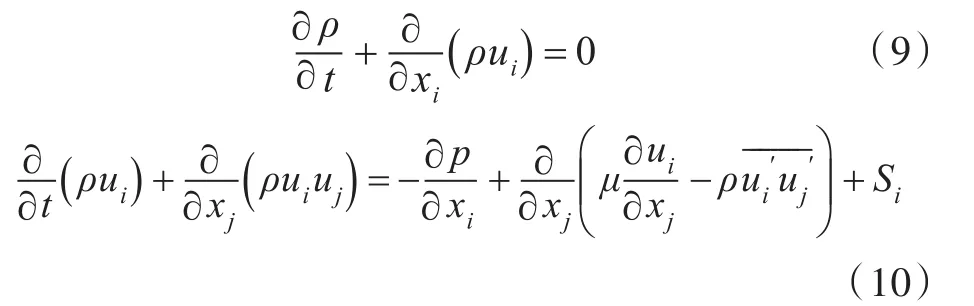
式中：i，j=1，2，3；μ为动粘性系数；xi，xj为笛卡尔坐标系下不同方向的分量；为速度分量脉动值；p为压力时均值；Si为动量方程广义源项；“—”表示对物理量取时间平均。

为使上述方程组封闭，需引入湍流模型（方程），此处选取Realizablek-ε两方程模型。

1.3.2 计算域的建立及网格划分

考虑到本文是对滑行艇直航阻力进行计算，以及艇体严格的对称性，为减小计算量，选取半船模型进行数值模拟。构建的计算域如图2所示。

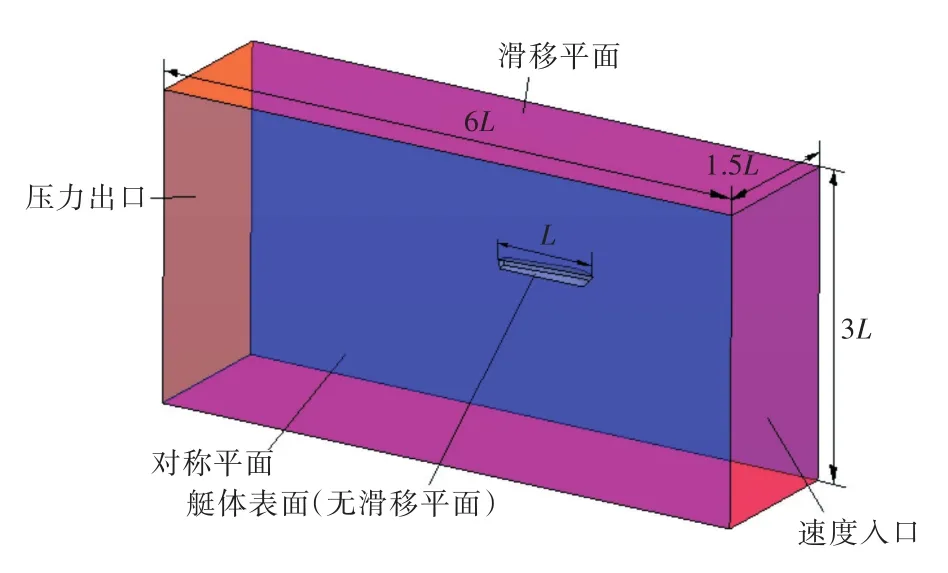
图2 计算域Fig.2 Computational domain for the planing craft model

选择切割体网格进行网格划分，在艇体附近和自由面附近进行适当加密，并观察网格质量是否符合要求。生成的艇体网格如图3所示，其中阴影密集部分即为加密区域。

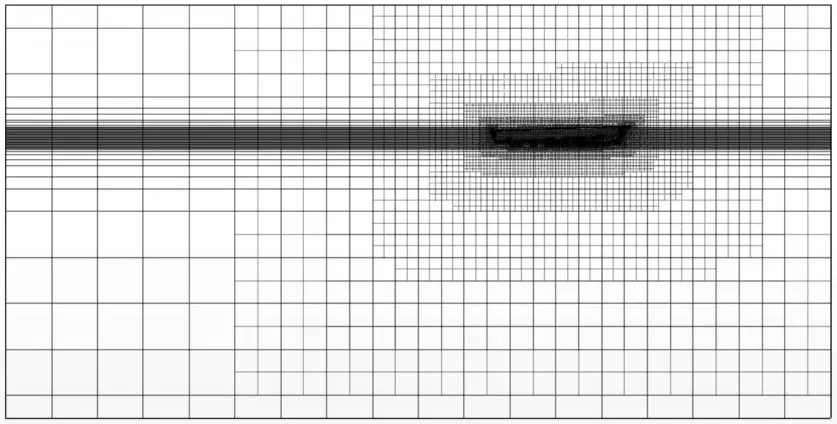
图3 网格划分Fig.3 Grid division of the planing craft model

1.3.3 物理模型的选取

STAR CCM+软件提供的流体体积法（VOF）波模型可供使用。VOF波模型通过在整个计算域内对互不相溶的两种流体求解同一组动量方程，并追踪每种流体的体积分数来模拟多相流，以使得采用STAR CCM+软件模拟船舶运动更简便。选取欧拉多相流、VOF波和重力等模型来模拟滑行艇运动时的受力情况。

1.3.4 初始条件及边界条件的设置

根据之前设置的VOF波模型相关场函数，设置流场的压力、速度和体积分数等初始条件，并对计算域边界的物理条件进行设定。

1.3.5 创建六自由体DFBI运动

选取DFBI模块模拟滑行艇的运动，建立原点位于重心的船体坐标系，以使得在滑行艇运动模拟中艇体绕重心做升沉和纵倾运动。

2 计算结果对比分析

本文分别使用查洁法、舒福德—勃朗法和CFD方法计算了15个不同静水速度（1.627，2.44，3.253，4.067，4.55，4.88，5.21，5.693，6.507，7.32，7.808，8.133，8.459，8.784和9.10 m/s）下同一滑行艇模型的阻力，并进行了船模阻力试验以验证所得结果。

2.1 船模阻力试验

船模阻力试验在中国特种飞行器研究所进行，根据所设计的型线，制作了滑行艇模型，并采用拖曳法对其阻力、升沉及纵倾角等数据进行了测量和记录。图4所示为在8.133 m/s速度下的滑行艇运动情况。

图4 滑行艇在拖曳水池中的运动情况Fig.4 Movement of the planing craft model in towing tank

2.2 半理论半经验方法计算结果对比分析

通过运用前述的半理论半经验方法，基于1.1节中给出的模型参数，计算得到的模型总阻力值Rt与试验值的对比如图5所示，纵倾角的对比如图6所示。图中，F▽为体积傅汝德数。

由图5可以看出，在整个速度区间内，半理论半经验方法的阻力计算结果的总体变化趋势均能与试验值大体保持一致；在高速滑行区间（F▽＞3.0），采用查洁法和舒福德—勃朗法均能较好地对滑行艇阻力值进行计算。在该区间内，查洁法的阻力计算结果与试验值更为接近，最大误差为5.61%，最小误差仅为0.11%，基本满足工程应用要求；而在F▽=3～4范围内，采用舒福德—勃朗法所得结果与试验值比较一致。由图6可以看出，采用半理论半经验方法可以反映出滑行艇纵倾角大致的变化趋势，但具体的计算结果与试验值相差较大，在大部分速度下二者的差值均在1°左右；而查洁法与舒福德—勃朗法相比能更好地反映真实情况下纵倾角随速度的变化。

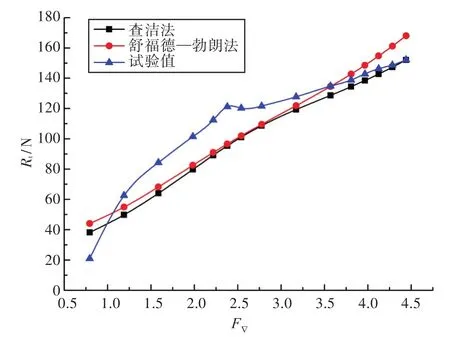
图5 半理论半经验方法阻力计算值与试验值对比Fig.5 Comparison of the analytical-experimental method results and experimental values about resistances

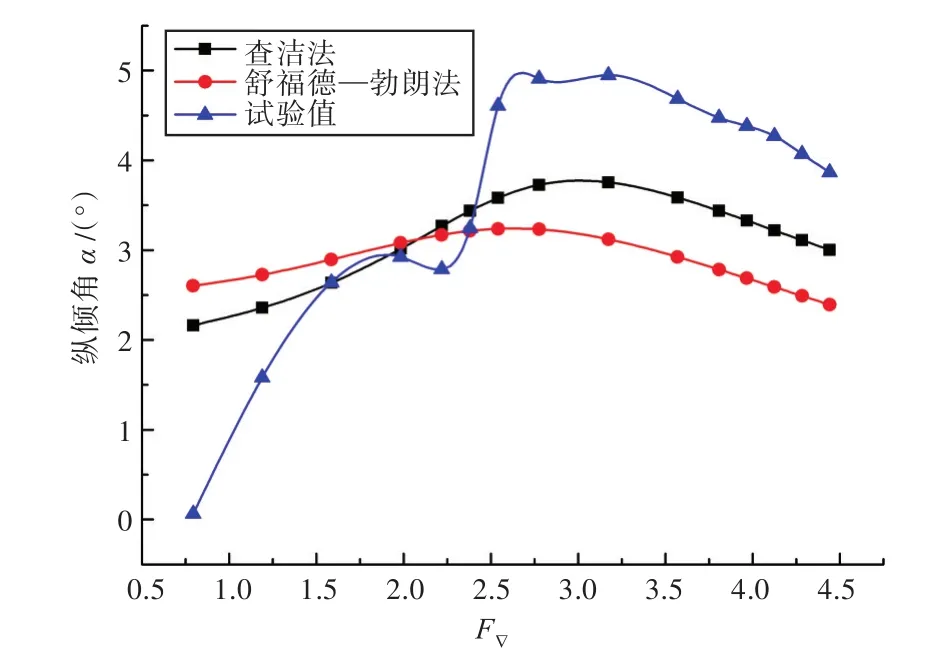
图6 半理论半经验方法纵倾角计算值与试验值对比Fig.6 Comparison of the analytical-experimental method results and experimental values about trims

2.3 CFD方法计算结果对比分析

采用1.3节所述方法，使用STAR CCM+软件对滑行艇模型阻力进行计算，所得结果与试验值的对比如图7所示，纵倾角的对比如图8所示。

由图7可见，采用CFD方法所得阻力计算值在大部分速度下与试验值均能较好地吻合，在滑行艇进入高速滑行稳定状态后，使用CFD方法可以达到较高的计算精度，其与试验值的相对最大误差为3.29%，且随着速度的增大，其计算精度明显提高，误差逐渐减小，最小误差仅为0.38%，符合工程应用标准。相比以往采用重叠网格的CFD滑行艇阻力计算方法，采用DFBI模块的方法操作简单，所需计算资源较少，同时阻力计算值也能获得较高的计算精度，不过纵倾角的计算结果与试验值相比误差较大。

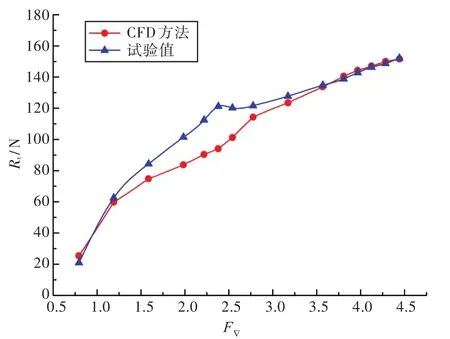
图7 CFD方法阻力计算值与试验值对比Fig.7 Comparison of the CFD method results and experimental values about resistances

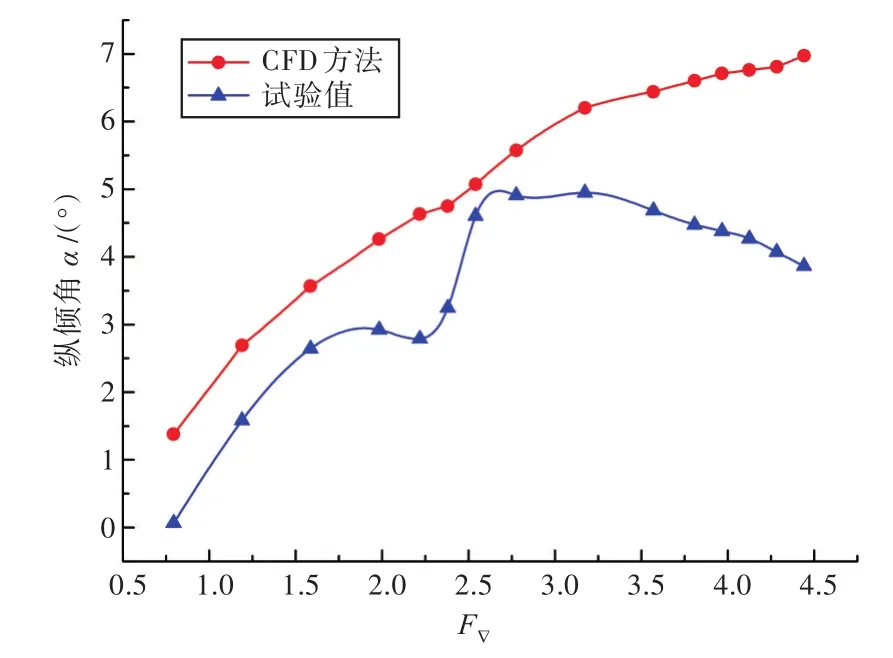
图8 CFD方法纵倾角计算值与试验值对比Fig.8 Comparison of the CFD method results and experimental values about trims

3 结 论

本文通过使用半理论半经验方法和CFD方法对某滑行艇模型进行阻力计算，并进行船模试验对比和验证，得到以下结论：

1）在高速滑行区间（F▽＞3.0），采用半理论半经验方法得到的总阻力计算结果可满足工程应用要求，其中采用查洁法的总阻力计算结果要优于采用舒福德—勃朗法的结果，采用舒福德—勃朗法的阻力计算结果仅在F▽=3～4范围内与试验值比较一致。纵倾角计算值的变化趋势与试验值相近，误差在1°左右。

2）基于STAR CCM+软件中的DFBI模块，采用CFD数值计算方法在大部分速度下均能得到较好的总阻力计算结果，且在高速滑行状态下可以达到较高的计算精度，但纵倾角的计算结果误差较大，仍有待改进。

本文的研究表明，基于STAR CCM+软件DFBI模块的CFD数值计算方法可以较好地实现该滑行艇型的阻力计算，并将进一步应用于后续相关滑行艇的阻力计算。在今后的工作中，将针对网格单元等因素对滑行艇阻力计算的影响进行研究，目前正在进行之中。