浮体浅水波浪载荷数值计算方法研究

杨鹏，寇冠元，朱学康，刘成义，高长华

1海南大学机电学院，海南海口570228

2武汉第二船舶设计研究所，湖北武汉430205

0 引 言

随着国家对南海开发和维护国家主权等需求的日益增强，需要在南海岛礁附近布置大型浮式平台，以供岛礁开发、综合执法补给和旅游等。岛礁附近的水深一般较浅，位于浅水中浮体的水动力运动和载荷响应与深水中的存在较大差别，因此，需要研究浅水中浮体在波浪中的运动和载荷响应。浅水中浮体与深水中浮体运动的最大差别和难点在于有限水深格林函数的准确求解。只有准确求解有限水深格林函数及其偏导数，才能得到浮体在波浪中的响应。Li［1］、谢永和等［2］和刘日明等［3］提出了数值积分方法，用来计算有限水深的格林函数及其导数。有限水深格林函数求解方法分为积分形式［4］和级数形式［5］2 种。其中积分形式的计算精度高，远场和近场均适用，但计算效率低；级数形式计算效率高，但在近场附近很难收敛，同时在远方辐射半径R=0处存在奇点。所以在计算有限水深格林函数及其导数时一般在近场采用积分形式，远场采用级数形式。

积分形式的解是主值积分且存在奇异性，这是有限水深格林函数及其导数求解的难点所在。传统的有限水深格林函数积分计算公式采用多点Gauss-Laguerre公式直接进行积分或多项式逼近。直接积分法一般需要取64个高斯积分点［1］方能满足精度要求，但该方法耗时长且误差较大，尤其是在高频率处计算失真。多项式逼近法（例如法国船级社的Hydrostar）需要计算大量的数据并选择适当的逼近区间，难以实施。本文拟通过推导和数值实验提出精确计算有限水深格林函数及其偏导数的方法，以解决高频失真问题。Newman［6］认为在半径和水深比R/H＞0.5时采用适当项数的级数解可以得到理想的精度，但其并没有给出小R/H的简化解。为了提高计算效率，本文拟给出对称性的处理方法和简化的级数求解公式的实施方案，并编制计算程序将本文方法与商业软件计算结果进行比较分析，以验证本文方法的正确性和可行性。

1 浅水复杂格林函数法

1.1 入射势求解

设一阶波面升高表达式为

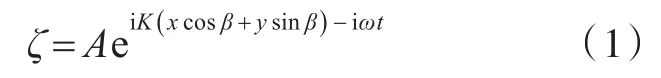
式中：A，K，ω和β分别为波幅、波数、波浪自然频率和浪向，例如，顶浪为180°。坐标系定义：x指向船艏，y指向船左舷，z垂直于静水面向上，xyz符合右手法则。

那么，入射势ΦI的一阶表达式为

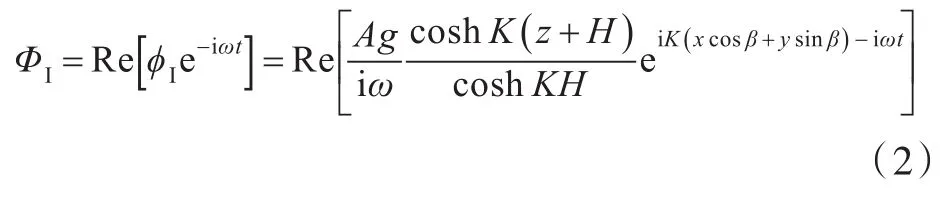
式中：ϕI为入射速度势的幅值；H为水深；g为重力加速度。

1.2 辐射势求解

无航速条件下，有限水深（均匀海底）的辐射势求解条件如下。

在流域内，

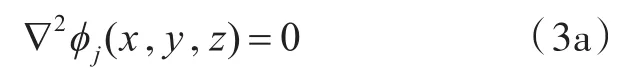
在z=0上，

在物面不可穿透条件下，

在水底不可穿透条件下，

远方辐射条件下，

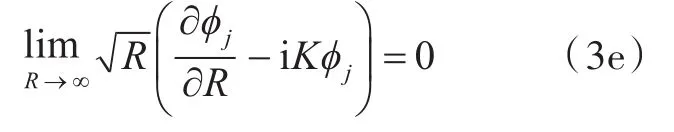
为了满足自由面边界条件、无穷远辐射条件和水底不可穿透条件，有限水深格林函数G一般采用如下2种形式。

1）积分形式［4］：

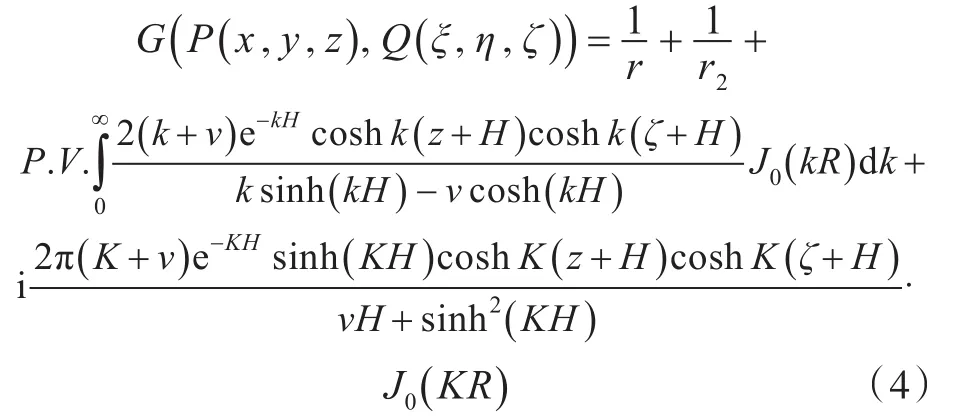
式中：P.V.为取主值积分；P(x，y，z)和Q(ξ，η，ζ)分别为场点和源点；k为积分变量；关于池底的镜像；J0()为第1类零阶Bessel函数。

2）级数形式［5］：

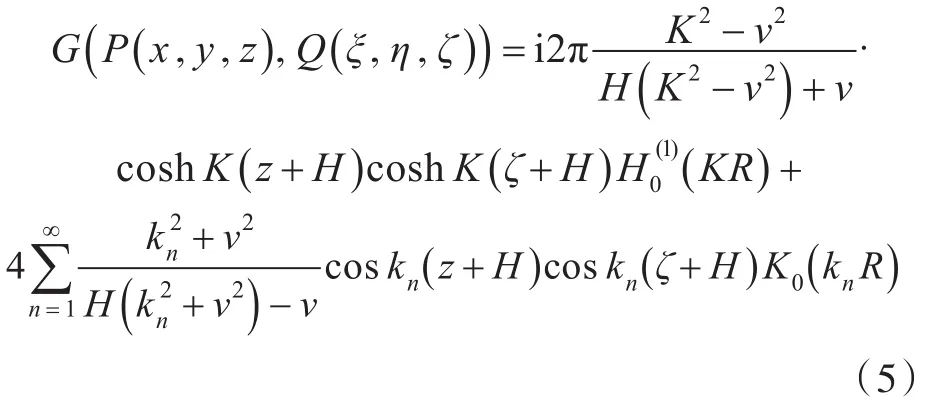
式中：kn为方程kntanknH+ν=0的正实根；为第1类零阶Hankel函数；K0()为第2类零阶修正的Bessel函数。

那么流域内各点的速度势为

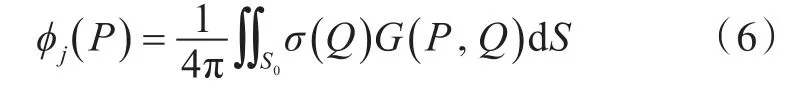
决定源强的积分表达式为

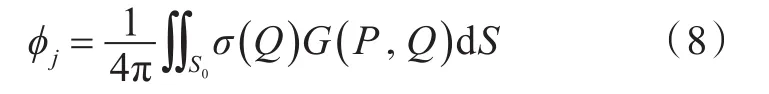
那么，附加质量μjk和附加阻尼λjk由下式求得：

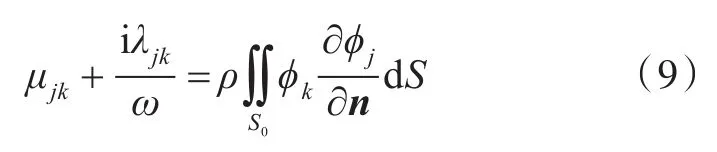
式中：ρ为流体密度；ϕk为辐射势。

1.3 绕射势求解

绕射势ϕD的求解方程为

在流域内，

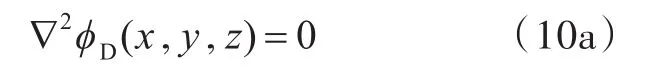
在z=0上，

在物面上，

在水底，

远方辐射条件下，

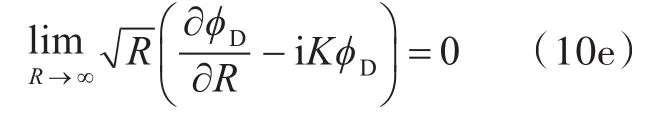
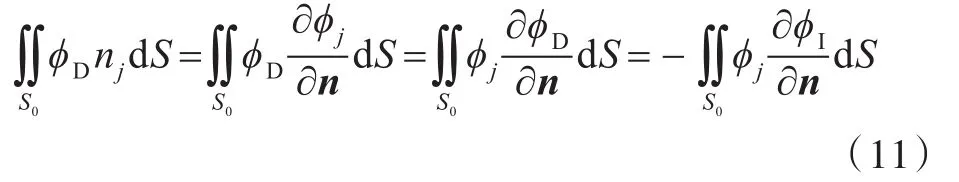
得到绕射势的计算公式为

因此，可以不必求解绕射势，直接由波浪入射势ϕI和辐射势ϕj求得波浪力。辐射势在前面已求得，第j阶波浪力（入射势+绕射势）的表达式为

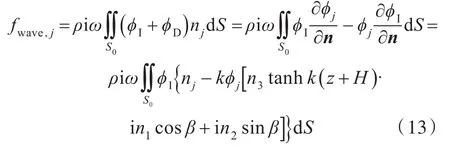
2 浅水波浪载荷数值计算方法

在浅水辐射势和绕射势的求解过程中，首先需要对格林函数及其导数进行求解。

2.1 格林函数的直接积分法

为了书写方便，式（4）和式（5）中的格林函数G及其偏导数的主值积分部分G0如下：

式中，J1()为第1类一阶Bessel函数。

式（14）～式（16）中不带奇异性的积分通过借鉴下式得到：

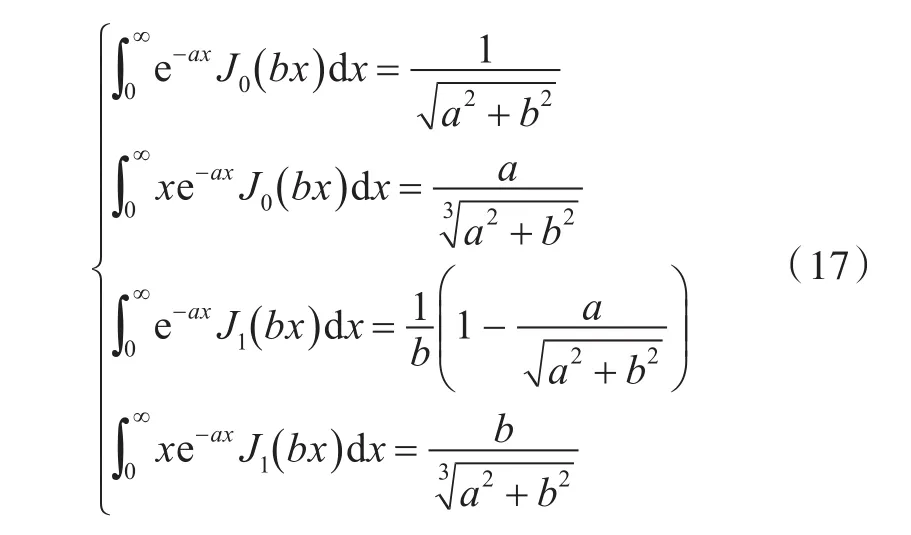
式中，a和b为广义变量。

为书写方便，引入

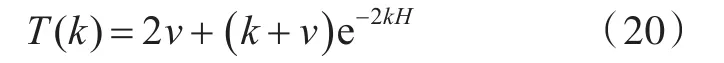
结合式（18）和式（19），可以得到

其中第1项积分无奇异，可以采用Gauss-Laguerre积分方法直接计算，第2项积分可以通过无限水深的格林函数计算公式得到，那么

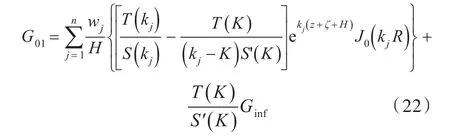
式中：wj为Gauss-Laguerre积分的权重系数；，为无限水深格林函数的积分公式。

2.2 格林函数的级数解

根据前文所述，浅水格林函数的求解公式可以采用如下级数解形式：

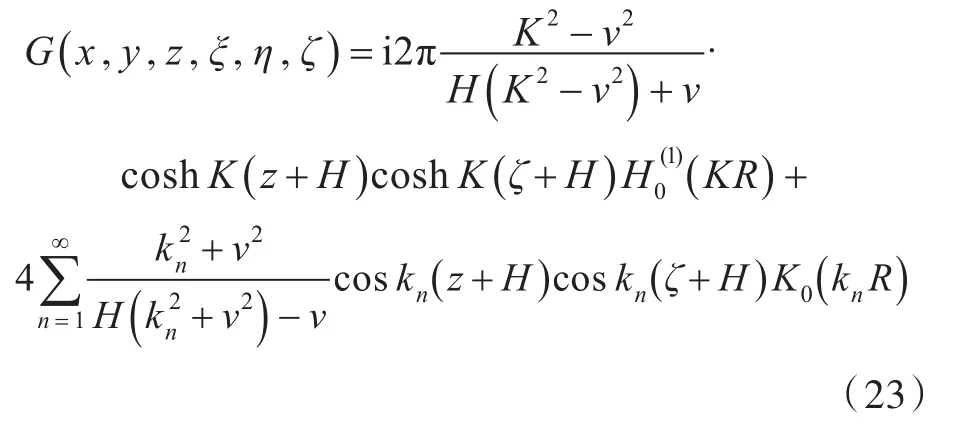
针对式（23）中的高阶级数项，有

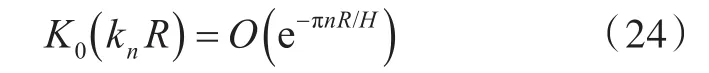
式（24）表明，式（23）的收敛速度取决于R H，当R/H=0时，式（23）将不收敛：

1）当R/H≥0.50时，如果式（23）的n=10，

2）当R/H≥0.25时，如果式（23）的n=20，

3）当R/H≥0.10时，如果式（23）的n=50，

因此，当R/H≥0.25时，可以选取适当项数的级数解来得到较为精确的值。Newman［6］证明了当R/H≥0.5时，采用级数解可以得到精度较高的近似值，级数项数一般取6H/R的整数。另外，当当knR≥8.0时，经过上述简化，相比于直接积分，可以较快速地计算出格林函数及其导数的值。

2.3 具有对称面的计算处理

对于具有对称面的物体，在计算时可以节省大量的内存和时间。在求解源强时，其系数矩阵为满秩矩阵，只能使用计算效率较低的高斯消元法和LU分解法等，其时间度为O(n3)，所以利用矩阵的对称性求解线性方程组能够极大地提高求解速度。当物体具有1个对称面时，方程可以转化为2个n/2阶的线性方程组问题，线性方程组的求解时间降为原来的1/4；当物体具有2个对称面时，方程可以转化为4个n/4阶的线性方程组问题，线性方程组的求解时间降为原来的1/16。下面，以具有2个对称面的浮体计算源强时的推导过程为例，具有1个对称面的情况与此类似。

为便于讨论，将物面上的点分成4个区域（图1）。

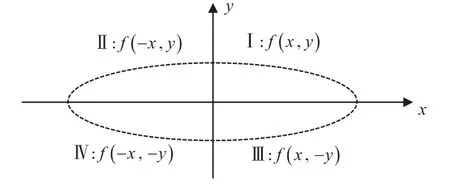
图1 浮体示意图Fig.1 Schematic diagram of floating body

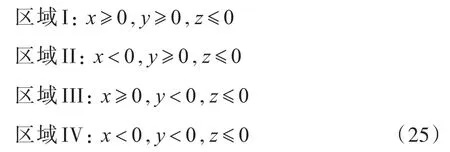
对于这类具有2个对称面（yz和xz平面）的物体，存在如下关系式：

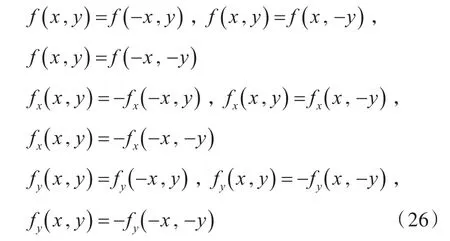
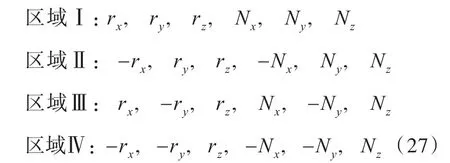
式中：i和j分别为场点和源点的面元序号；角标ϕ为速度势。

设在区域I上有N个单元，那么整个物面的平均湿表面上共有4N个单元。从式（29）～式（33）可以看出，并不需要计算整个物面的速度势矩阵G0，G0x，G0y，G0z和G0n，只需对每个矩阵计算4个N×N矩阵。对于具有2个对称面（yz和xz平面）的湿表面来说，可采用式（33）求解源强的系数矩阵。该矩阵为循环矩阵，可将原方程组的求解化为4个N阶矩阵的方程组来求解［8］，下面介绍具体的计算方法。

式中，{ni}为第i个面元的法向。

定义4N阶矩阵P4N和P2N为

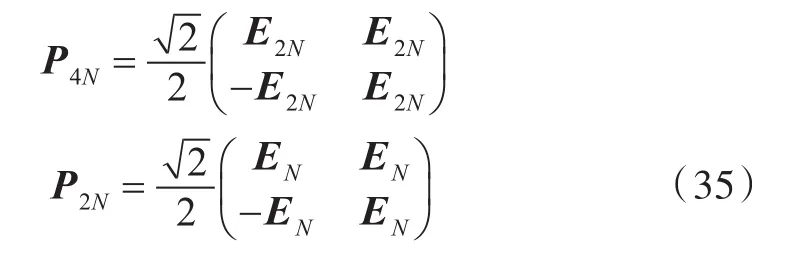
式中，E2N和EN分别为2N阶和N阶单位矩阵。P4N可将G0n对角化，即

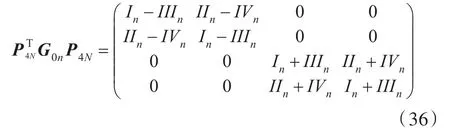
P2N可将式（36）对角化为

源强的线性求解方程组变换为

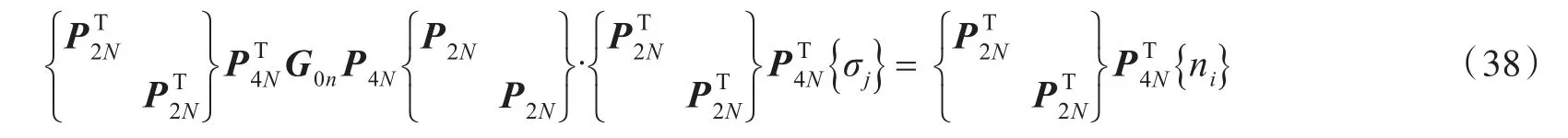
将式（37）代入式（38），可得

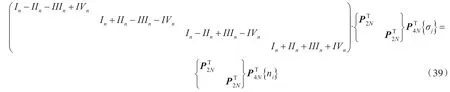
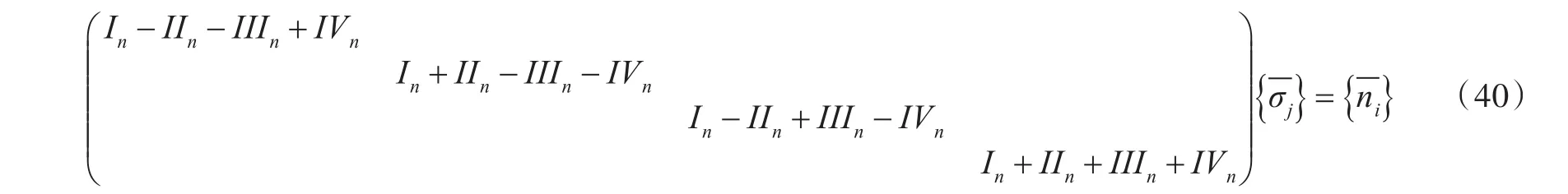
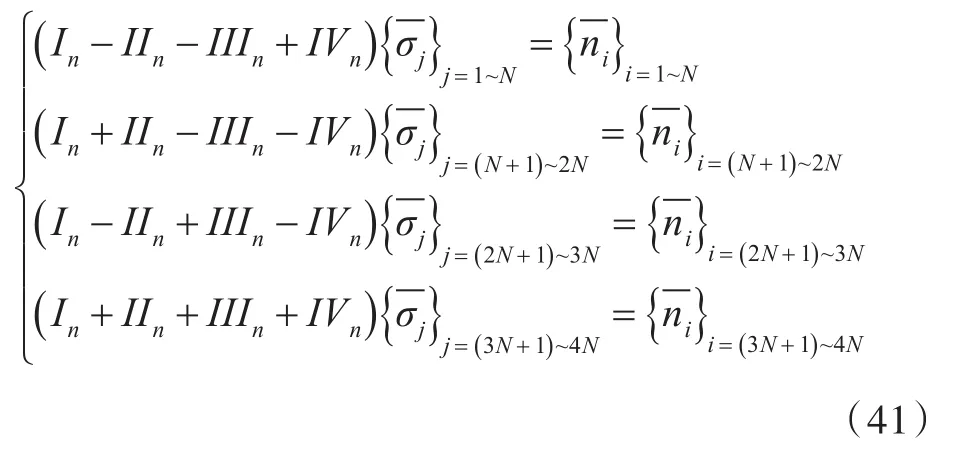
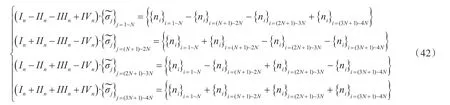
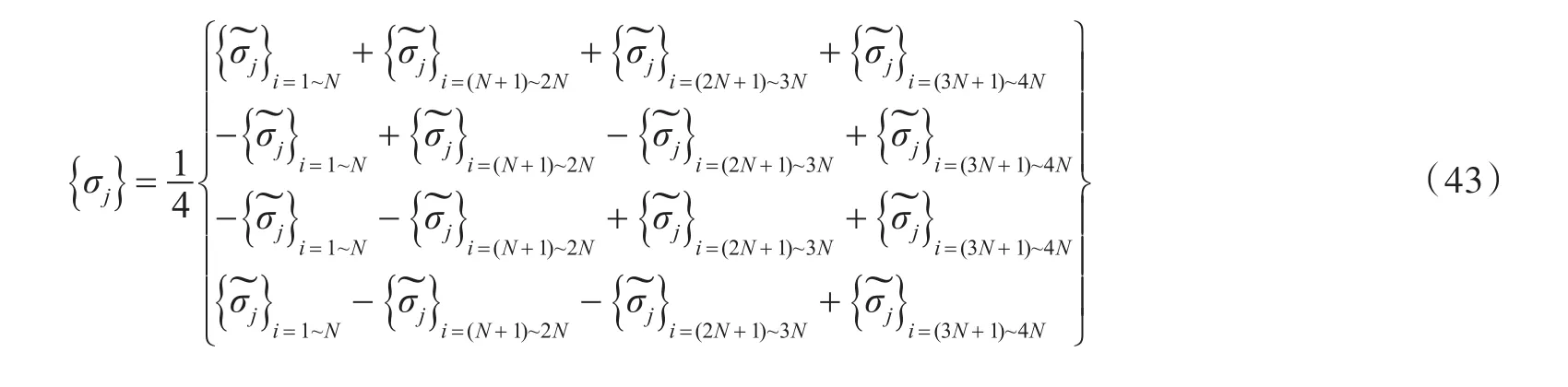
3 波浪载荷计算方法

3.1 浮体表面的波动压力

应用面元法分别求解得到辐射势ϕj（j=1，2，3，4，5，6）之后，便可通过规则波中的浮体运动方程获得稳态的运动响应ηj（j=1，2，3，4，5，6），那么非定常辐射势ϕR和绕射势ϕD便随之确定。浮体表面的波动压力除了由波浪入射势、辐射势和绕射势引起的脉动压力，还将包含由浮体运动引起的浮体表面静水压力变化ps项，总的脉动压力为［9］

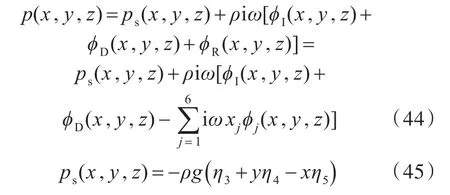
式中，η3，η4和η5分别为浮体的垂荡、横摇和纵摇运动。

3.2 浮体横剖面的波浪载荷

确定了规则波中的浮体运动响应之后，便可应用达朗贝尔原理计算浮体横剖面的力和力矩，包括波浪诱导的垂向弯矩与水平的剪力和弯矩以及轴力和扭矩。

3.2.1 部分长度浮体的刚体惯性力载荷

以浮体x轴与横剖面的交点为坐标原点O，选取单位长度的浮体，设其质量为μ(x)，质心坐标为(x，y，z) ，其惯性质量矩阵为

式中：Ixx，Iyy，Izz，Ixy，Ixz和Iyz为关于坐标x，y，z的惯性矩（积）；Sx≡μx，Sy≡μy，Sz≡μz，均为刚体质量关于坐标平面的静矩。

任意横剖面x处至船艏xf之间的质量对横剖面的刚体惯性力载荷为

式中，{}为浮体六自由度运动加速度。

3.2.2 浮体横剖面的力和力矩

作用于任意横剖面x处至船艏xf之间部分长度浮体上的真实流体载荷与横剖面上的力相互平衡，那么横剖面上的载荷为

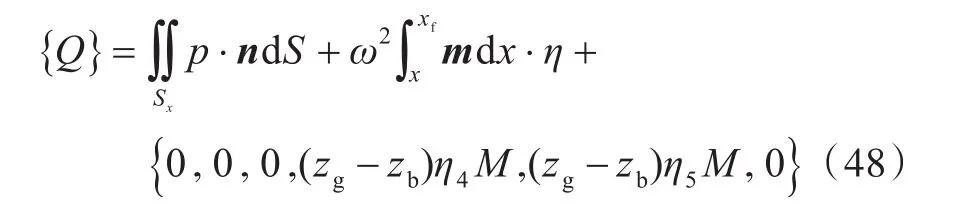
式中：Sx，M，zb和zg分别为横剖面x处至船艏xf之间部分长度浮体的湿表面、质量、浮心和重心的z坐标；p为流体压力；η为浮体六自由度运动幅值。

4 浅水数值计算结果对比分析

4.1 箱型浮体计算结果

针对ISSC（2006）［10］标准浮箱进行了运动传递函数的计算，其主尺度和计算结果如表1和图2所示。

本次计算的1/4模型网格数为155个。从图2可以看出，针对无限水深和20 m水深，本文程序计算结果与采用商业软件AQWA获得的计算结果十分吻合，验证了本文计算方法的正确性。

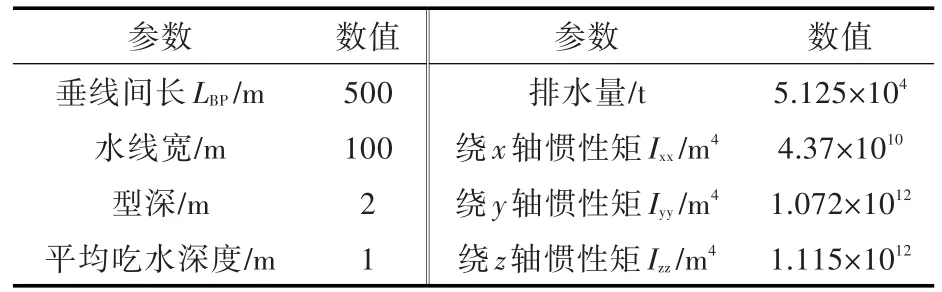
表1 浮箱主尺度Table 1 Main dimensions of box

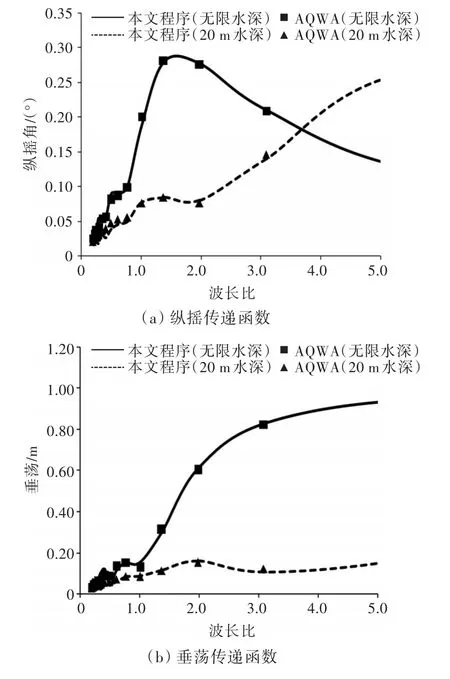
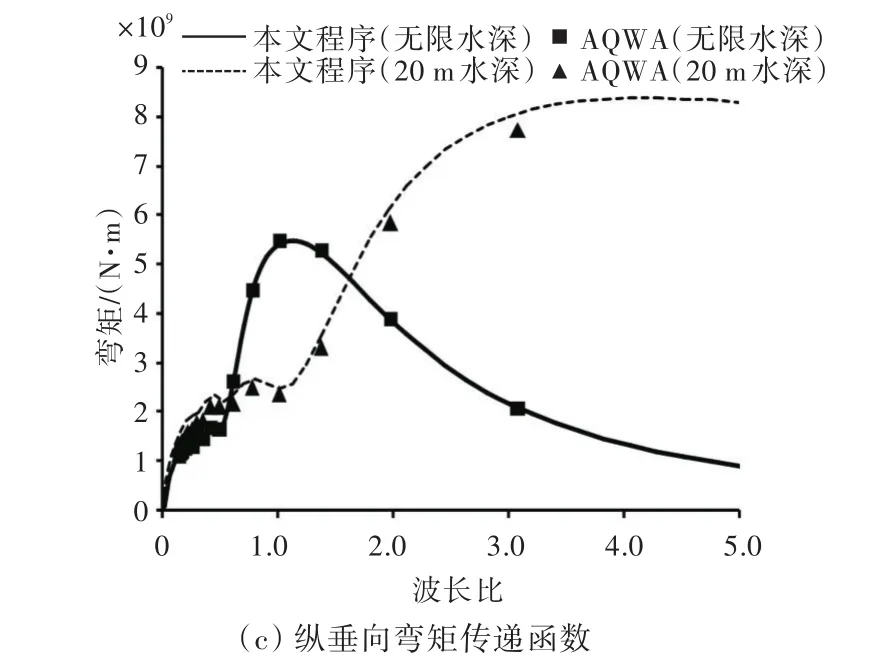
图2 箱型浮体运动和载荷传递函数（0°浪向）Fig.2 Transfer function of motion and loads of box（0°wave direction）

4.2 大型散货船计算结果

针对一艘20.5×104t大型散货船，计算了零航速（压载）工况下纵摇和垂荡传递函数，其主尺度和计算结果如表2和图3所示。

本次计算的半模型网格数为440个。从图3可以看出，针对无限水深和40 m水深，本文程序计算结果与采用商业软件Wadam获得的计算结果十分吻合，验证了本文计算程序和方法的正确性。

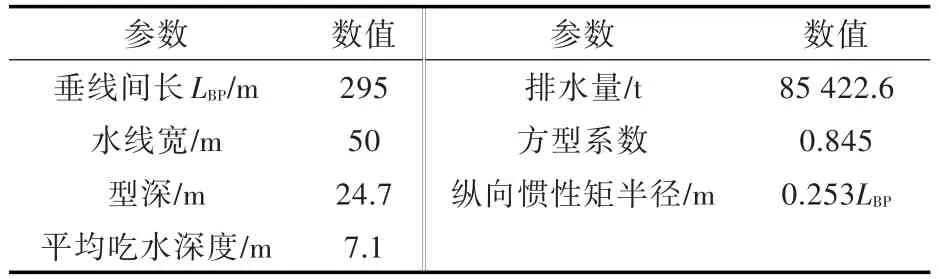
表2 散货船主尺度Table 2 Main dimensions of bulk carrier

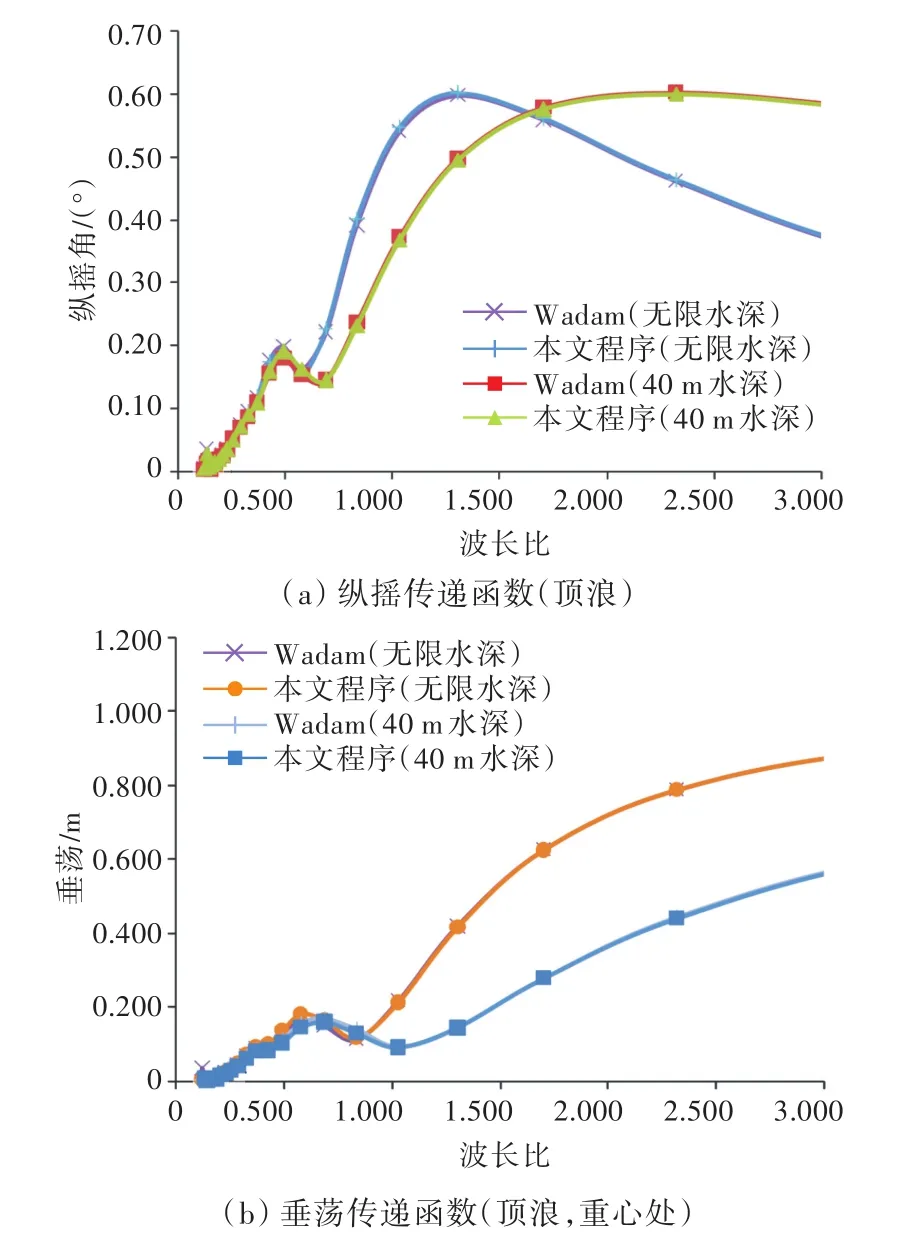
图3 散货船运动传递函数Fig.3 Transfer function of motion of bulk carrier

5 结 语

基于势流理论和边界元方法，给出了速度势求解方程，同时利用循环矩阵原理对复杂格林函数进行了严谨的求解推导和对称性处理研究，从而建立了浮体在浅水中运动和波浪载荷的完整计算方法。本文给出的改进方法和思路可以精确计算格林函数及其导数，同时通过研究有限水深格林函数的级数解形式，给出了简化的快速计算方法。针对具有对称面的浮体，引入循环矩阵进行严格数学推导，发现利用对称性得到简化后的辐射势求解方法可节省大量计算时间。

通过自主开发程序进行数值计算，并与成熟商业软件结果进行对比分析，验证了本文给出的有限水深格林函数计算方法和相应计算程序的正确性。本文建立的计算方法对浅水中的浮体运动和波浪载荷评估具有重要意义。