船舶运动与液舱晃荡耦合频域计算方法
孙雷,罗贤成,刘昌凤,姜胜超
1大连理工大学船舶工程学院,辽宁大连116024
2高新船舶与深海开发装备协同创新中心,上海200240
3大连海洋大学海洋与土木工程学院,辽宁大连116023
0 引 言
船舶运动与液舱内流体的晃荡会产生相互作用,特别是对于液化天然气船(LNG)和浮式生产储油卸油设备船(FPSO)等含有大型液舱的船舶,其具有较大的液舱,并且液舱的固有频率接近于船舶运动频率,会导致液舱内流体产生的晃荡作用更加明显。因此,在载液船舶的设计初期,就应该考虑船舶运动与液舱内流体晃荡的耦合作用影响。近年来,有关船舶与液舱晃荡耦合作用的研究已有较大进展。Francescutto和 Contento[1]通过对载液船舶在横浪工况下进行规则波作用下的模型实验,证明液舱内液体晃荡自由面的存在会对船舶运动产生影响。Rognebakke等[2]通过对液舱进行横荡实验,获得了稳定状态下液舱横荡运动与线性入射波频率之间的线性关系。Molin等[3]通过计算载有液舱的LNG船,得到了船舶运动与舱内液体自由水面的变化情况。Newman[4]开发的WAMIT程序可用于计算线性液舱晃荡与船舶运动耦合情况。KIM等[5]采用脉冲响应函数(IRF)求解线性船舶运动,采用有限差分方法模拟非线性液舱的晃荡问题,并与载有方形液舱的S175船舶横摇运动实验结果进行了对比,结果显示吻合较好。操戈等[6]考虑了液舱内流体的粘性,发现所得结果与试验值更接近。
本文将采用频域计算方法研究船舶运动与液舱晃荡耦合作用问题。在频域方法中,对于船舶运动方程,采用自由面格林函数方法进行求解;对于液舱内流体晃荡过程,采用Rankine源方法进行求解。为提高计算精度,本文将采用高阶边界元方法进行离散,应用8节点等参数单元进行频域求解,并以文献[7]中装载2个液舱的船舶模型为例,将本文计算结果与采用水动力软件HYDROSTAR所得结果、文献[8]的数值计算结果及文献[7]的实验数据进行对比,以验证本文计算方法的准确性。
1 运动预报理论
1.1 船舶运动
船舶在波浪上的运动预报是研究船舶运动与液舱流体晃荡的基础,且波浪幅值与船舶特征尺度相比是小量,流体的粘性影响很小,波浪绕射力对船舶影响较大。因此,在研究船舶在波浪中的运动姿态时,基于势流理论,流体通常可以假设为均匀、不可压缩、无粘、无旋的理想流体。
波浪中的参考坐标系如图1所示。其中,固定坐标系为大地坐标系o0-x0y0z0,平面x0o0y0与船舶静水面重合,o0z0轴垂直向上;船舶位置参考系为o′-x′y′z′,o′x′轴位于中纵剖面,指向船艏为正,o′y′轴指向右舷为正,o′z′轴垂直向上;船舶动坐标系为o-xyz,oz轴垂直向上,当船有航速时,该坐标系随船以平均速度移动,代表着船舶运动形态。
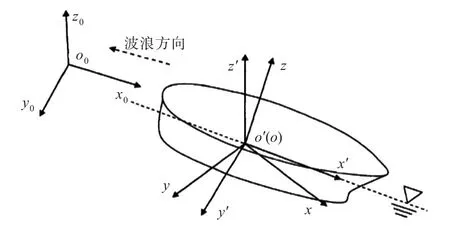
图1 船舶运动坐标系Fig.1 The coordinate system for ship motions
根据三维线性势流理论,采用一阶近似,分布在船舶周围的速度势函数满足线性边界条件与拉普拉斯方程。当船舶静止在自由水面上摇荡时(无航速),流场中的一阶不定常速度势ϕ可以分解为
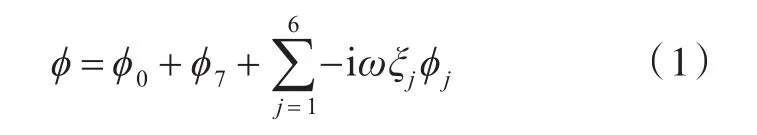
式中:ϕ0为入射势;ϕ7为绕射势;ϕj为j自由度上的辐射势;ω为波浪圆频率;ξj为在j自由度上的位移;i为虚数单位。
入射势可取AIRY线性波,绕射势与辐射势的规范化定解条件满足拉普拉斯方程(式(2))与边界条件(式(3)和式(4))。

在船体表面SB上,
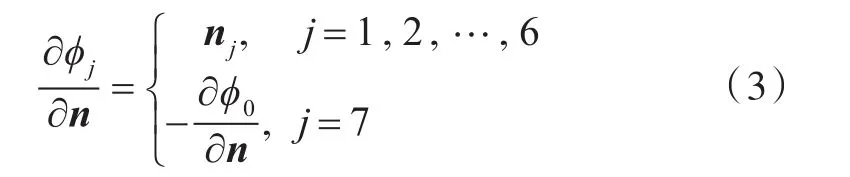
在自由水面SF上,

式中:g为重力加速度;n为网格单元垂直方向;j为各个自由度。
应用格林第二定理,将源点布置在船体表面,并在船体表面建立边界积分方程:
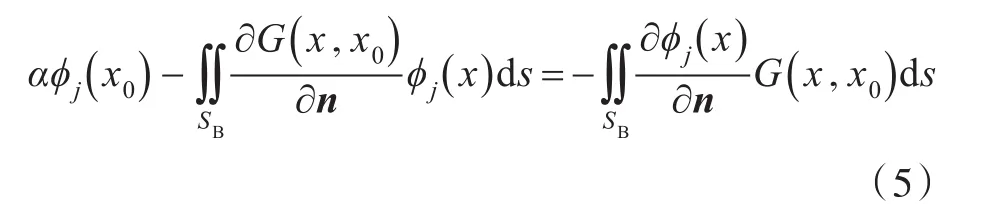
式中:α为自由项系数(固角系数),对于常单元,α=1/2,对于高阶边界元,α随体表面变化;G为自由面格林函数,也即Havelock源格林函数。
本文采用边界元法将频域内的积分简化为仅在船体表面积分,大大减小了计算时间和数据存储时间,并采用高阶边界元法离散上述积分方程,使表面离散成等参数单元,然后代入积分方程进行求解,便可得到速度势大小。得到速度势值后,在船体瞬时湿表面上进行伯努利积分,便可得到船舶湿表面瞬时波浪载荷
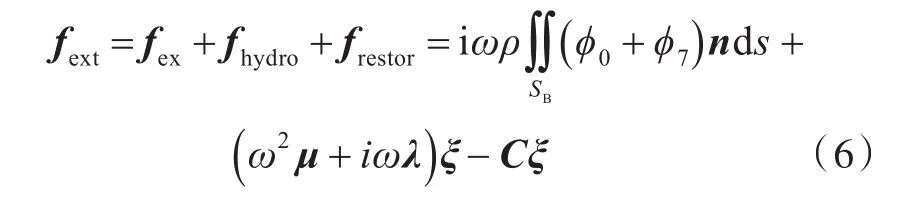
式中:fex为波浪激振力矩阵;fhydro为辐射力矩阵;frestor为回复力矩阵;μ为附加质量矩阵;λ为辐射阻尼系数矩阵;C为静回复力系数矩阵;ξ为船舶位移矩阵。
获得船舶水动力系数后,可建立船舶运动方程(式(7)),得到船舶在各个自由度上的运动位移
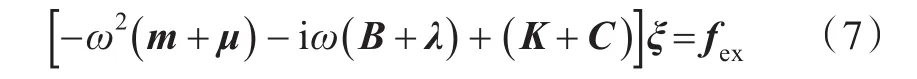
式中:m为广义质量矩阵;B为船舶系统阻尼矩阵;K为船舶系统刚度矩阵。
1.2 液舱流体晃荡
研究舱内流体的流动时,选取如图2所示的坐标系。液舱计算用动坐标系o-xyz,原点位于舱内自由水面中心;参考坐标系o′-x′y′z′不随物体而摇晃,当物体处于平衡位置时,其与动坐标系重合;固定坐标系o0-x0y0z0固定于空间某点,不随模型运动而变化。基于线性势流理论,舱内流体运动满足拉普拉斯方程与以下边界条件。
在液舱壁面ST上,
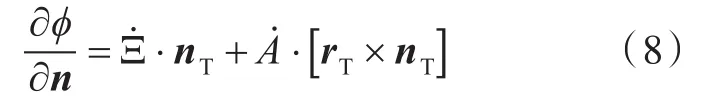
在自由水面SF上,
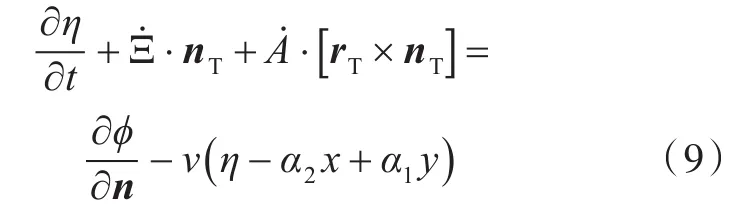
在船体表面SB上,
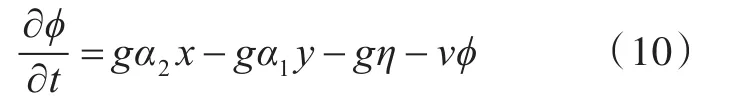
式中:Ξ =(ξ1,ξ2,ξ3),为液舱平动位移(动坐标系相对于参考坐标系);A=(α1,α2,α3),为液舱转动位移(动坐标系相对于参考坐标系);rT为位置矢量(相对于参考坐标系原点);nT为方向矢量;η为舱内液体波面升高;v=ωk,为考虑自由水面的阻尼系数[9],其中k为经验系数。
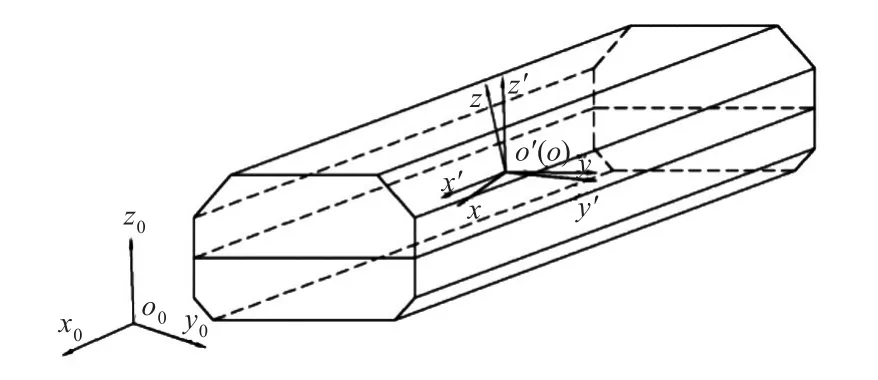
图2 液舱运动坐标系Fig.2 The coordinate system of the tank
根据线性关系,可将速度势函数进行分解:
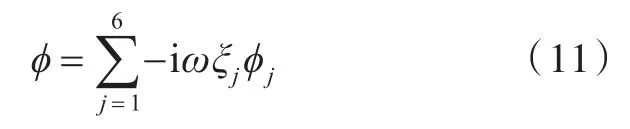
液舱的边界条件可以写为:
在液舱壁面ST上,
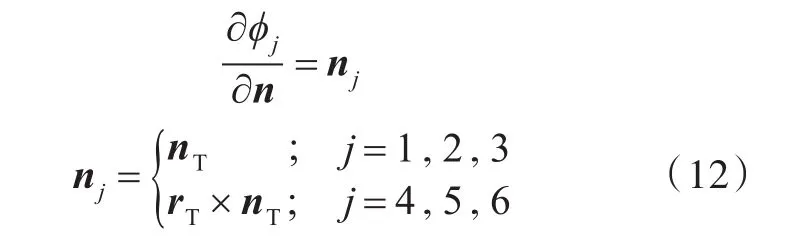
在自由水面SF上,
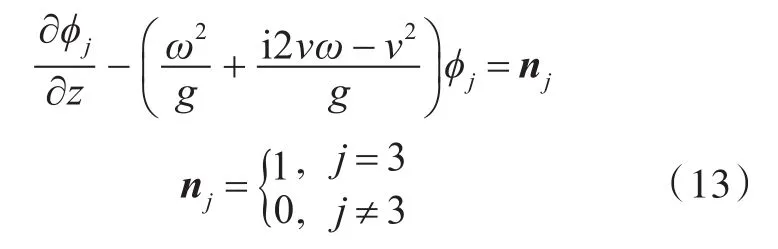
应用格林定理,建立边界积分方程:

式中,G为格林函数,为简便计算,采用简单Rankine源格林函数。
同样,采用高阶边界元法对上述积分方程进行离散求解,可以得到速度势。将速度势代入伯努利方程,沿着舱内瞬时湿表面进行积分,便可得到舱内波浪激振力
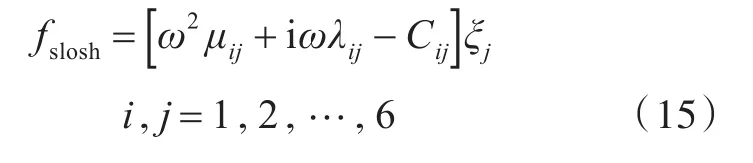
1.3 船舶运动与液舱流体晃荡耦合作用
通过上述研究,综合考虑船舶运动与液舱晃荡影响,建立频域运动下船舶与液舱晃荡耦合运动方程为
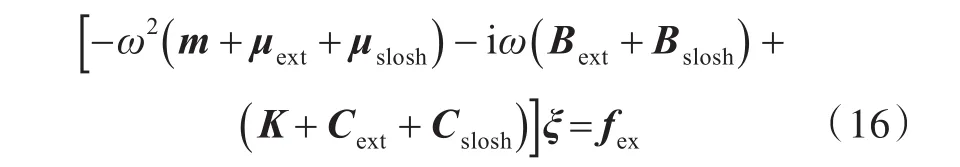
式中:μext为外部波浪激励的附加质量矩阵;μslosh为液舱流体晃荡的附加质量;Bext为外部波浪激励的阻尼矩阵;Bslosh为液舱流体晃荡的阻尼矩阵;Cext为外部波浪激励的静回复力系数矩阵;Cslosh为液舱流体晃荡的静回复力系数矩阵。
本文考虑两者耦合作用计算的流程图如图3所示。
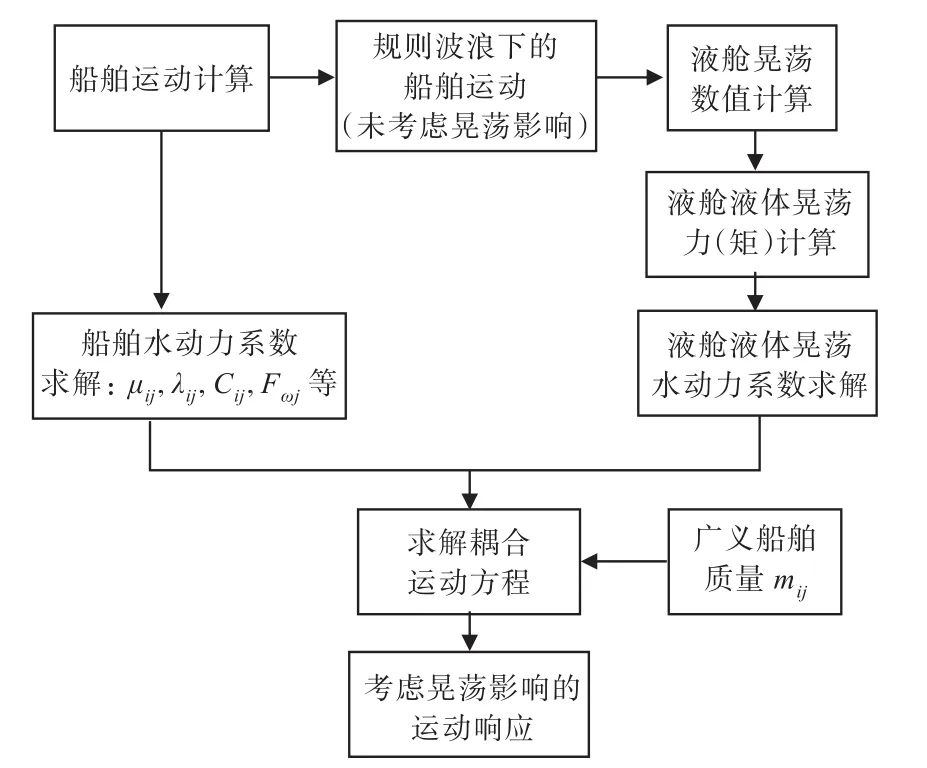
图3 计算流程示意图Fig.3 Flow chart for numerical simulation
2 验证计算
2.1 波浪与三维结构物作用
本文以某艘FPSO船型为例,计算在规则波浪中,船舶在各自由度上的运动幅值响应算子(RAO),并将本程序计算结果与采用HYDROSTAR,AQWA软件等计算的结果进行了对比,以验算本程序计算的准确性。
2.1.1 计算模型
该计算船型的主尺度参数如表1所示,网格模型如图4所示。
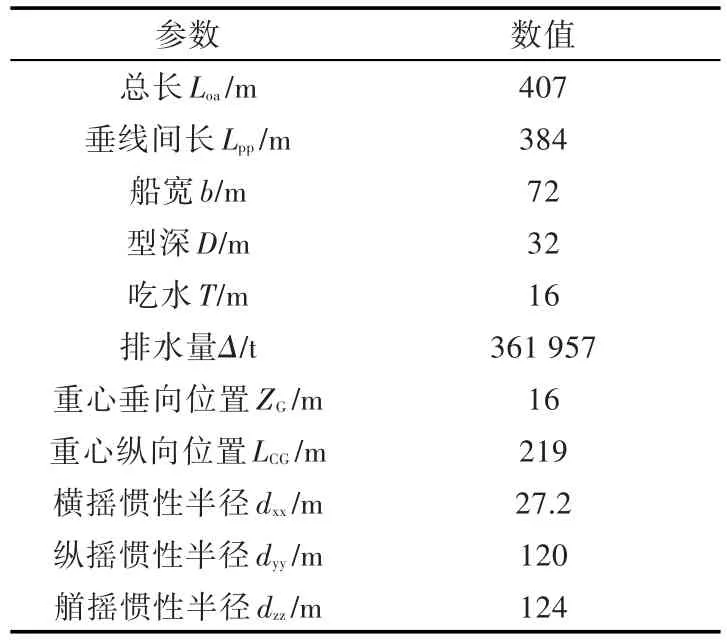
表1 FPSO船型主尺度参数Table 1 The main parameters of FPSO ship

图4 船体网格计算模型Fig.4 The computational model of ship
2.1.2 计算结果与分析
选取横浪(波浪与船艏方向夹角为90°)与迎浪(波浪与船艏方向夹角为180°)这2种工况,用本程序计算船舶在规则波作用下的运动响应,并分别与HYDROSTAR和AQWA软件计算的水动力计算结果进行对比,结果如图5~图8所示。图中,PRESENT指本文计算结果,HYDROSTAR指采用HYDROSTAR软件计算的结果,AQWA指采用AQWA软件计算的结果,图中纵坐标分别为3个自由度上的运动幅值响应算子[10]。

图5 90°浪向下横摇运动响应Fig.5 Rolling RAO in 90°wave direction angle
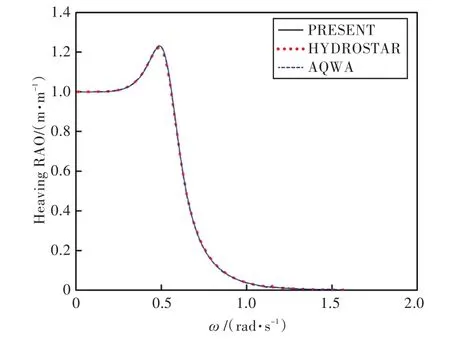
图6 90°浪向下垂荡运动响应Fig.6 Heaving RAO in 90°wave direction angle

图7 180°浪向下纵摇运动响应Fig.7 Pitching RAO in 180°wave direction angle

图8 180°浪向下垂荡运动响应Fig.8 Heaving RAO in 180°wave direction angle
图9~图14所示为横浪作用下船舶6个自由度上的波浪激振力(力矩)对比。
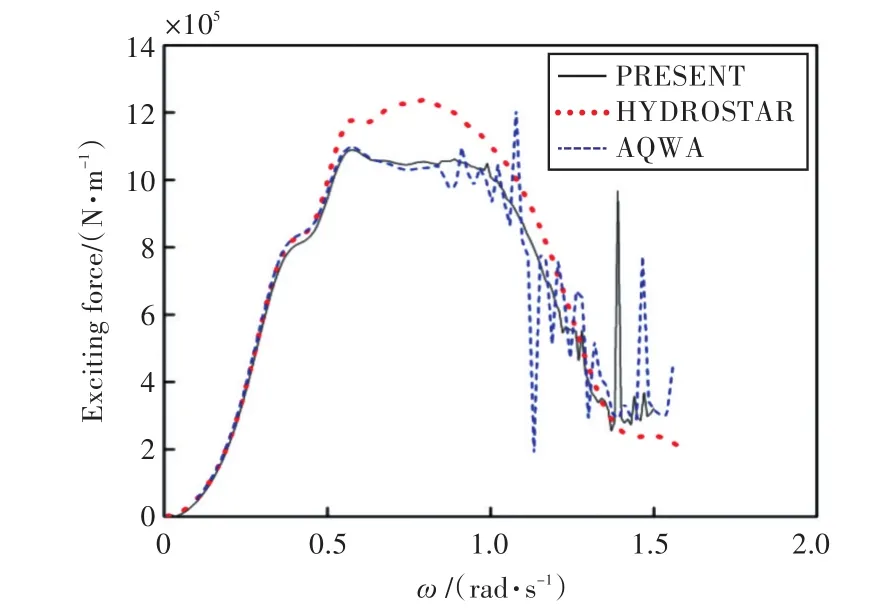
图9 x轴的波浪激振力Fig.9 Wave exciting force in the x axis
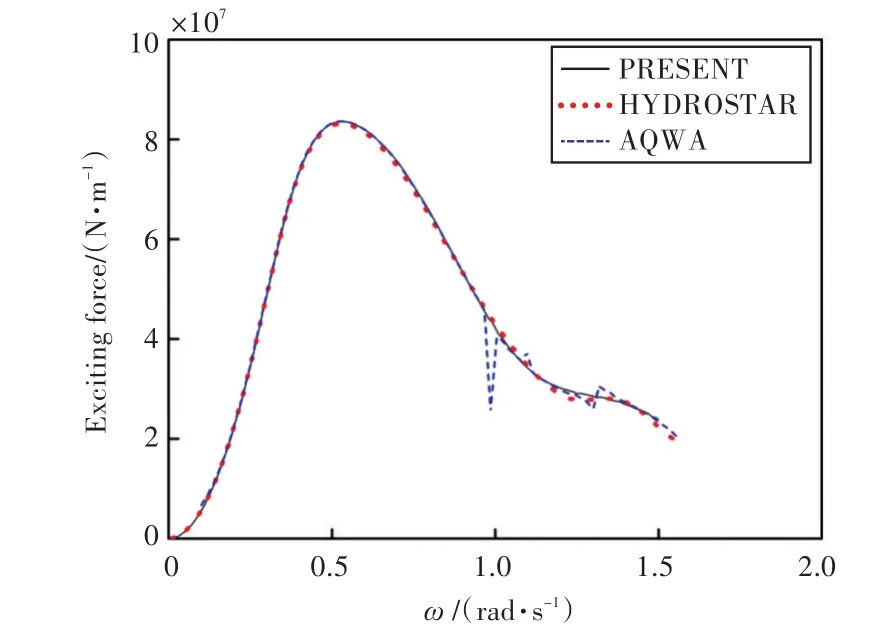
图10 y轴的波浪激振力Fig.10 Wave exciting force in the y axis
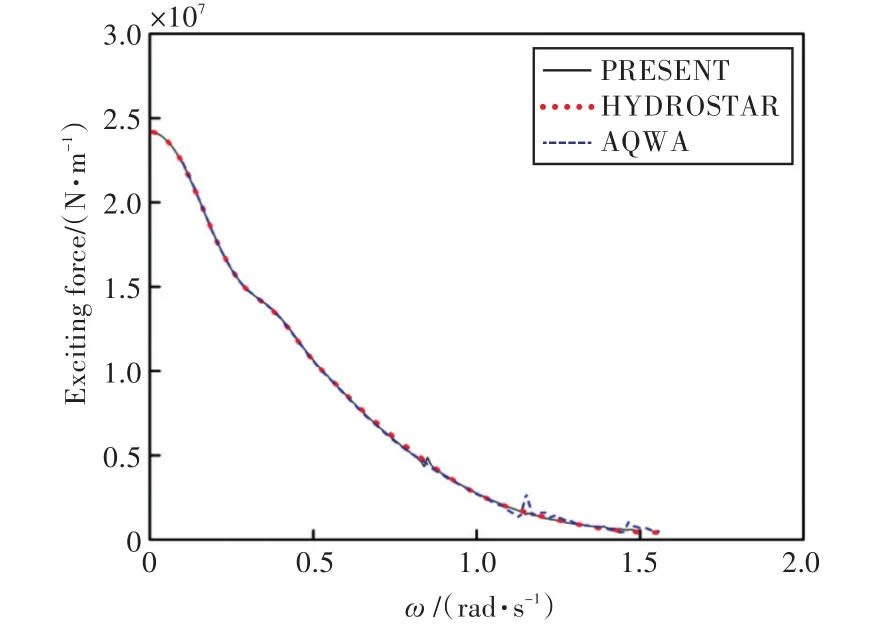
图11 z轴的波浪激振力Fig.11 Wave exciting force in the z axis
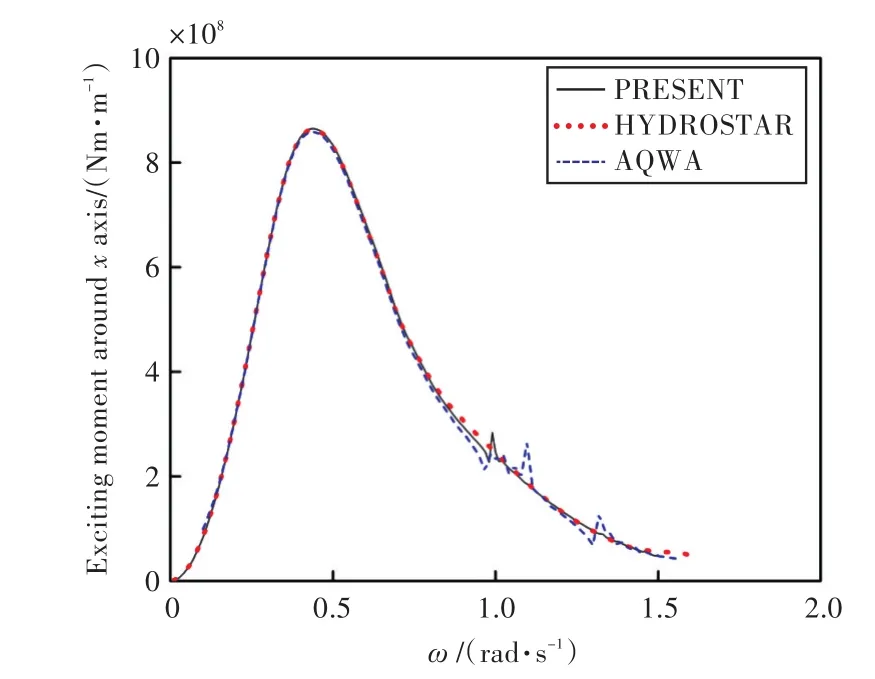
图12 绕x轴的波浪激振力矩Fig.12 Wave exciting moment around the x axis
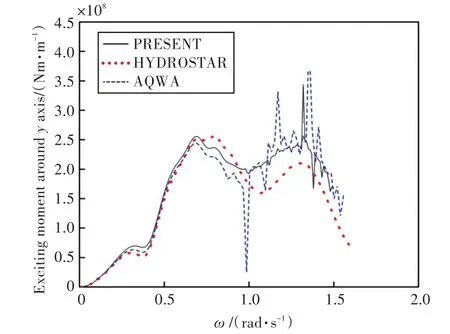
图13 绕y轴的波浪激振力矩Fig.13 Wave exciting moment around the y axis
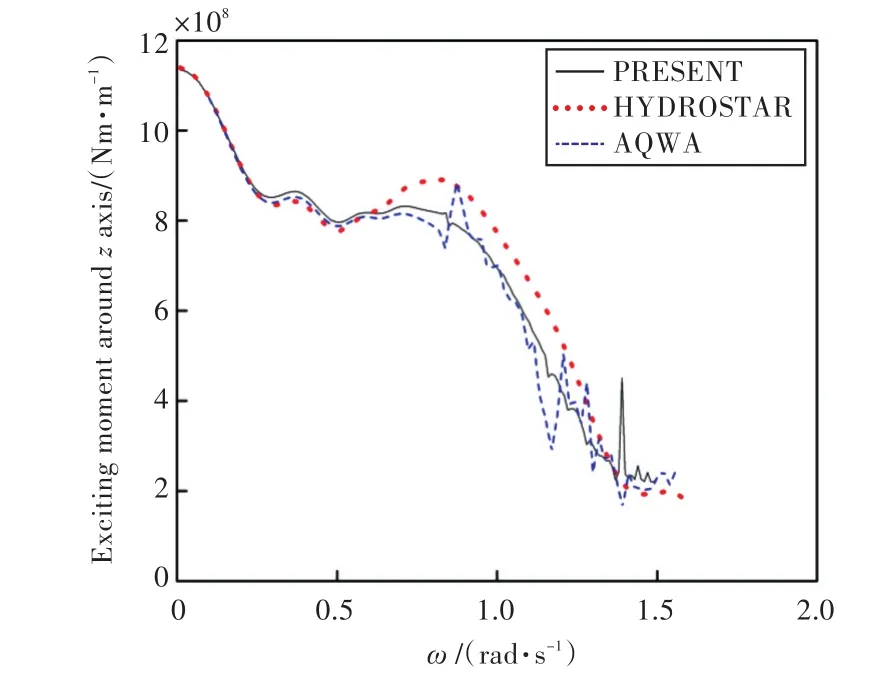
图14 绕z轴的波浪激振力矩Fig.14 Wave exciting moment around the z axis
由图可知,本文程序计算所得船舶在各自由度上的运动响应和波浪激振力与HYDROSTAR和AQWA水动力软件计算的结果吻合较好,证实了本文计算程序的准确性,也为下文进行船舶与液舱晃荡耦合运动提供了较好的基础。
2.2 考虑液舱晃荡的船舶运动
本文以某艘带2个液舱的FPSO船型为例,分别计算前、后液舱在不同装载率下的运动响应。
2.2.1 计算模型
选取的计算船型与液舱的主尺度参数分别如表2和表3所示。该船型与液舱(左舱为前舱)的平面视图如图15所示(图中数值单位为m),网格计算模型如图16所示。
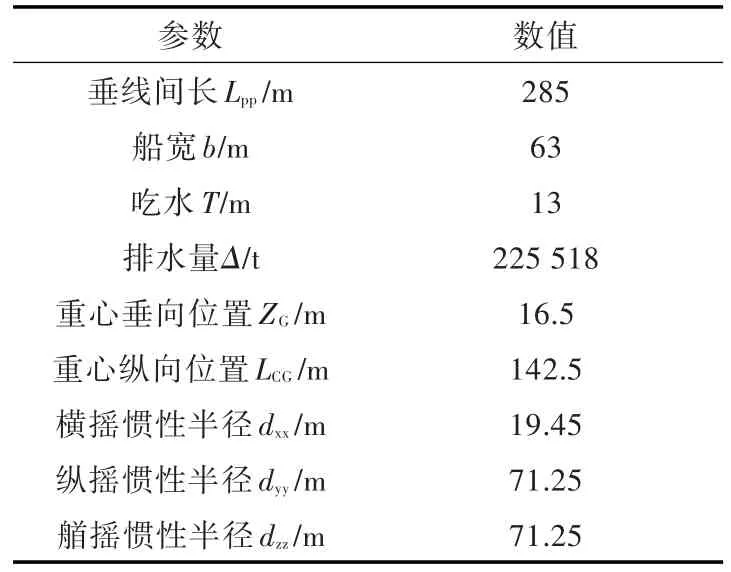
表2 FPSO船型主尺度参数(带2个液舱)Table 2 The main parameters of FPSO ship with two tanks
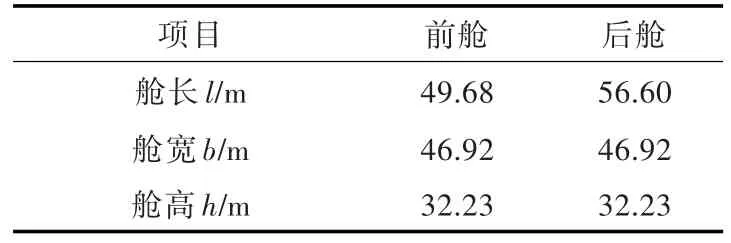
表3 液舱主尺度参数Table 3 The main parameters of the tank
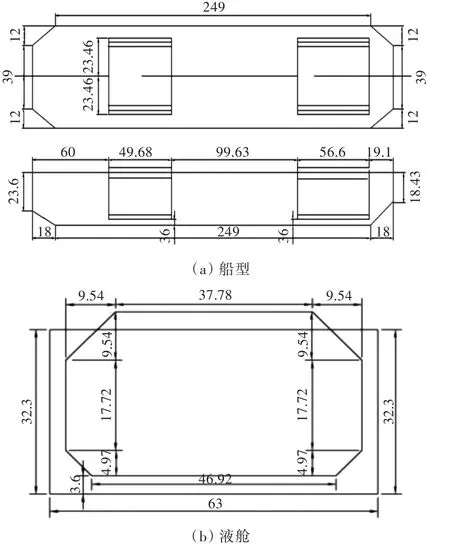
图15 船型与液舱的平面视图Fig.15 The plane view of the ship and tanks

图16 船型与液舱耦合网格计算模型Fig.16 The computational model of the ship and tanks
2.2.2 计算结果与分析
本文选取装载液体为水,计算无液舱装载(装载率为0)以及前、后液舱装载率分别为(20%,20%),(30%,30%)和(57.5%,43.3%)时,船舶在浪向为 90°,120°,180°时各自由度下的运动幅值响应算子(基于船舶重心处),并与水动力软件HYDROSTAR计算结果、文献[8]的数值模拟结果以及文献[7]的实验数据进行对比,计算结果如下。
图17~图22所示为该该耦合船舶在无装载情况下,浪向分别为 90°,120°和 180°时的运动响应幅值。
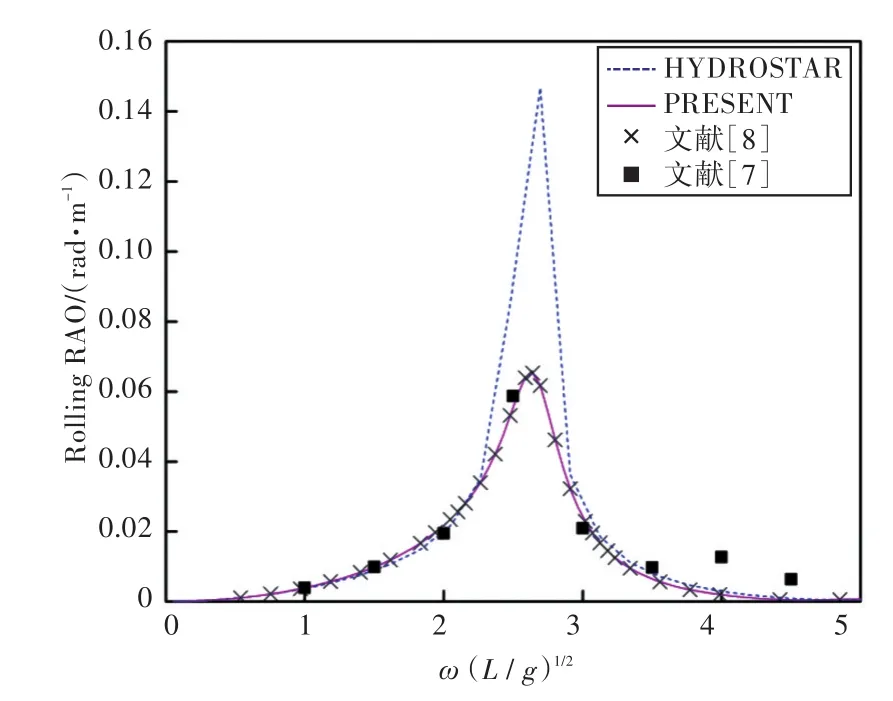
图17 90°浪向下横摇运动响应(无装载)Fig.17 Rolling RAO in 90°wave direction angle(0 filling)
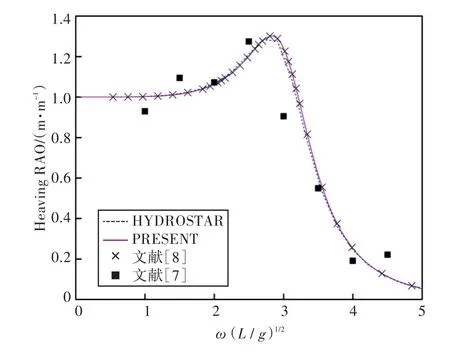
图18 90°浪向下垂荡运动响应(无装载)Fig.18 Heaving RAO in 90°wave direction angle(0 filling)
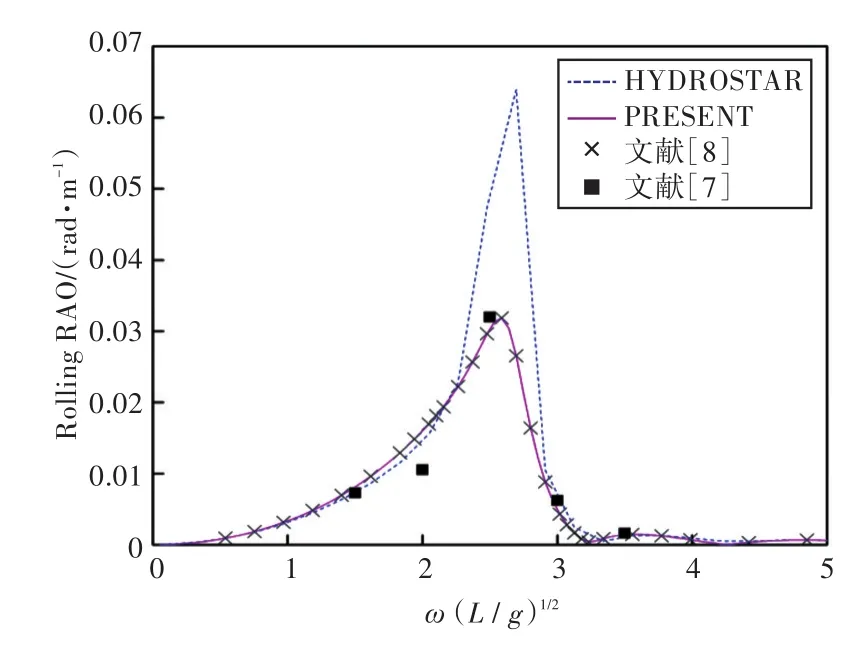
图19 120°浪向下横摇运动响应(无装载)Fig.19 Rolling RAO in 120°wave direction angle(0 filling)
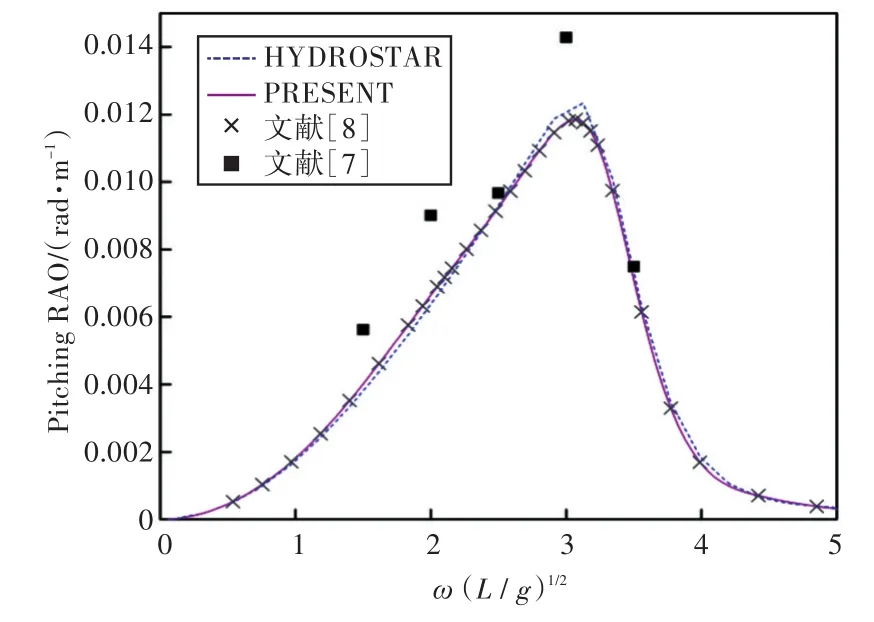
图20 120°浪向下纵摇运动响应(无装载)Fig.20 Pitching RAO in 120°wave direction angle(0 filling)
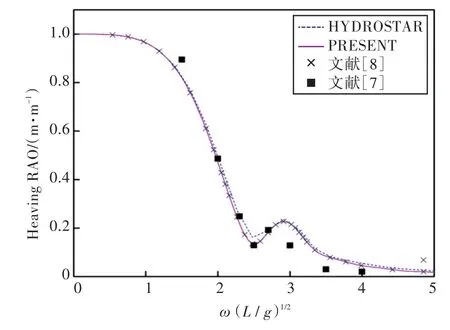
图21 180°浪向下垂荡运动响应(无装载)Fig.21 Heaving RAO in 180°wave direction angle(0 filling)
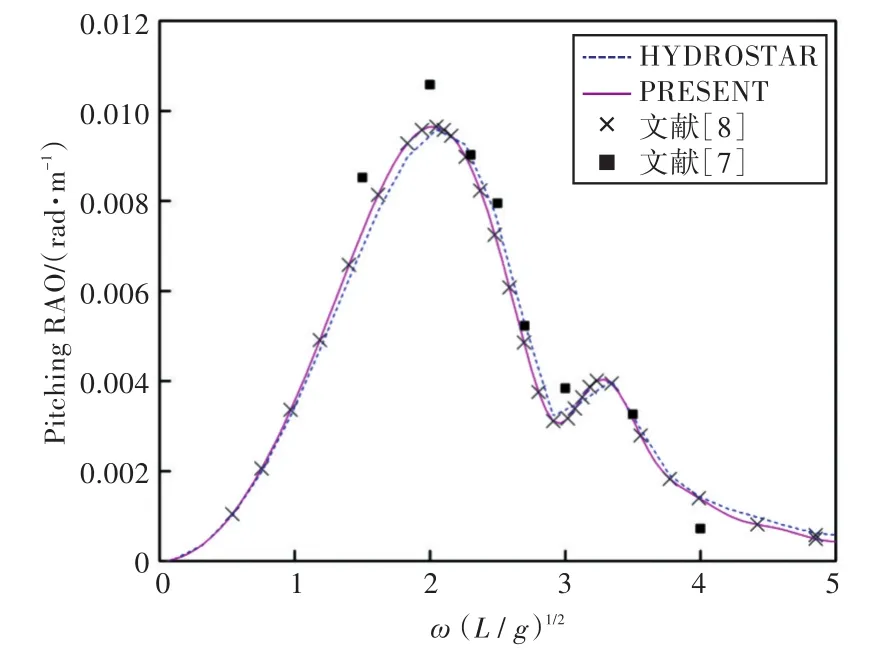
图22 180°浪向下纵摇运动响应(无装载)Fig.22 Pitching RAO in 180°wave direction angle(0 filling)
图23~图28所示为该耦合船舶在前、后舱装载率为(20%,20%)情况下,浪向分别为90°,120°和180°时的运动响应幅值。
图29~图34所示为该耦合船舶在前、后舱装载率为(30%,30%)情况下,浪向分别为90°,120°和180°时的运动响应幅值。
图35~图40所示为该耦合船舶在前、后舱装载率为(57.5%,43.3%)情况下,浪向分别为90°,120°和180°时的运动响应幅值。
图41所示为在90°浪向下,该耦合船舶在液舱不同装载率下的横摇运动响应对比图。
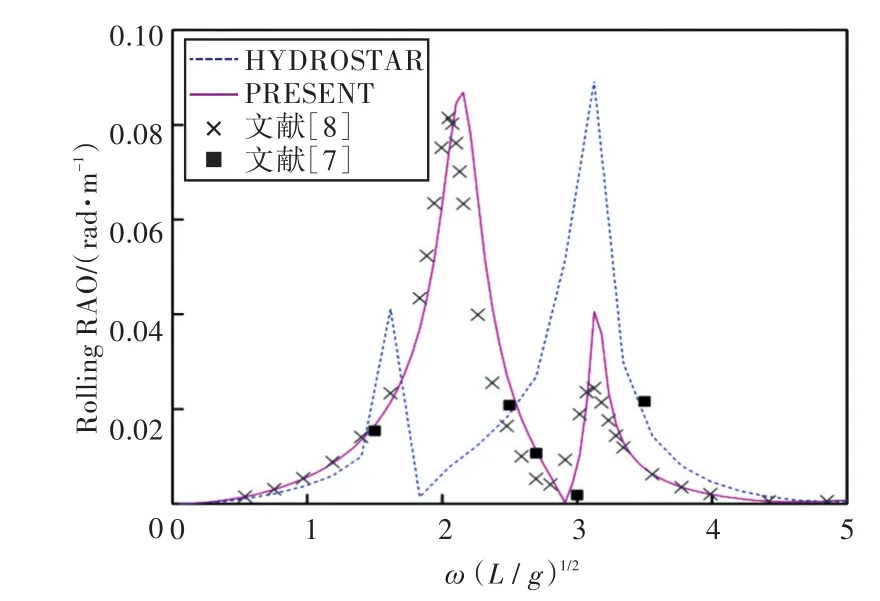
图23 90°浪向下横摇运动响应(前、后舱装载率为20%,20%)Fig.23 Rolling RAO in 90°wave direction angle(filling ratio of fore and back tank is 20%,20%)
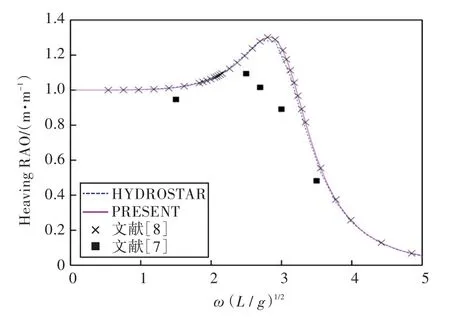
图24 90°浪向下垂荡运动响应(前、后舱装载率为20%,20%)Fig.24 Heaving RAO in 90°wave direction angle(filling ratio of fore and back tank is 20%,20%)
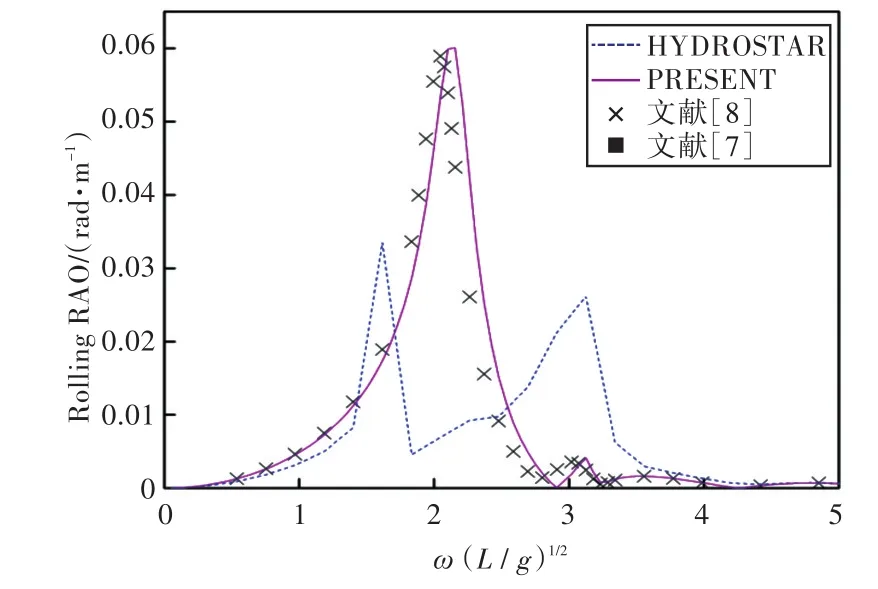
图25 120°浪向下横摇运动响应(前、后舱装载率为20%,20%)Fig.25 Rolling RAO in 120°wave direction angle(filling ratio of fore and back tank is 20%,20%)
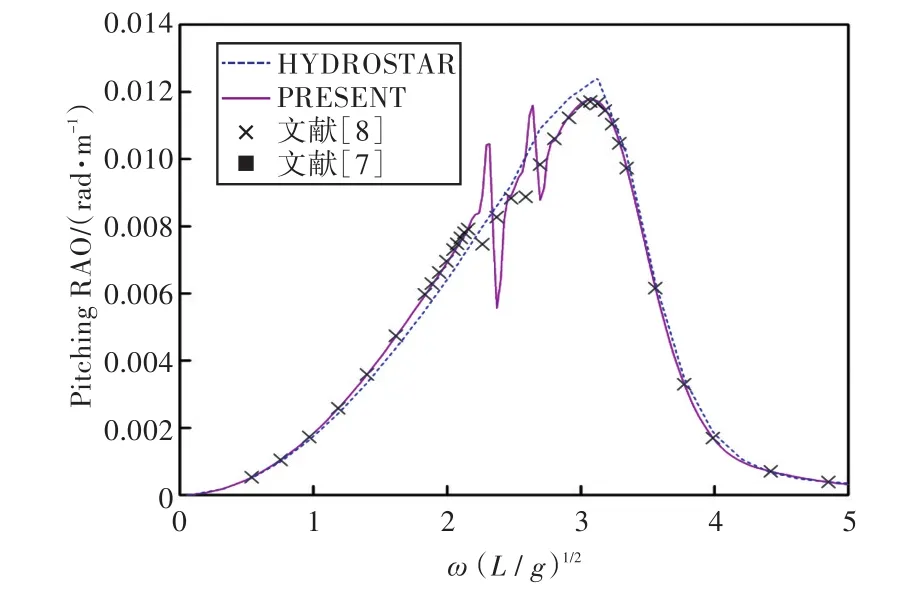
图26 120°浪向下纵摇运动响应(前、后舱装载率为20%,20%)Fig.26 Pitching RAO in 120°wave direction angle(filling ratio of fore and back tank is 20%,20%)
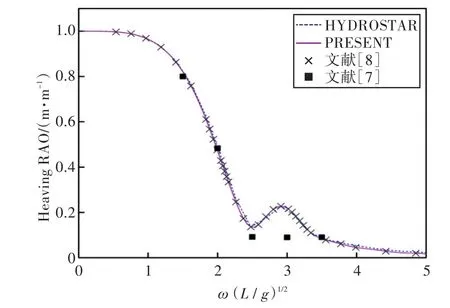
图27 180°浪向下垂荡运动响应(前、后舱装载率为20%,20%)Fig.27 Heaving RAO in 180°wave direction angle(filling ratio of fore and back tank is 20%,20%)
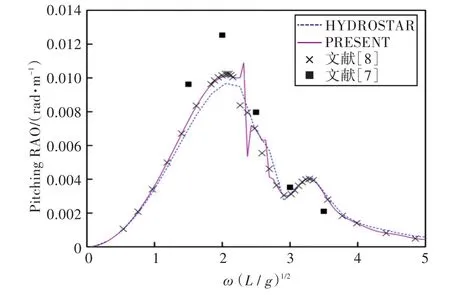
图28 180°浪向下纵摇运动响应(前、后舱装载率为20%,20%)Fig.28 Pitching RAO in 180°wave direction angle(filling ratio of fore and back tank is 20%,20%)
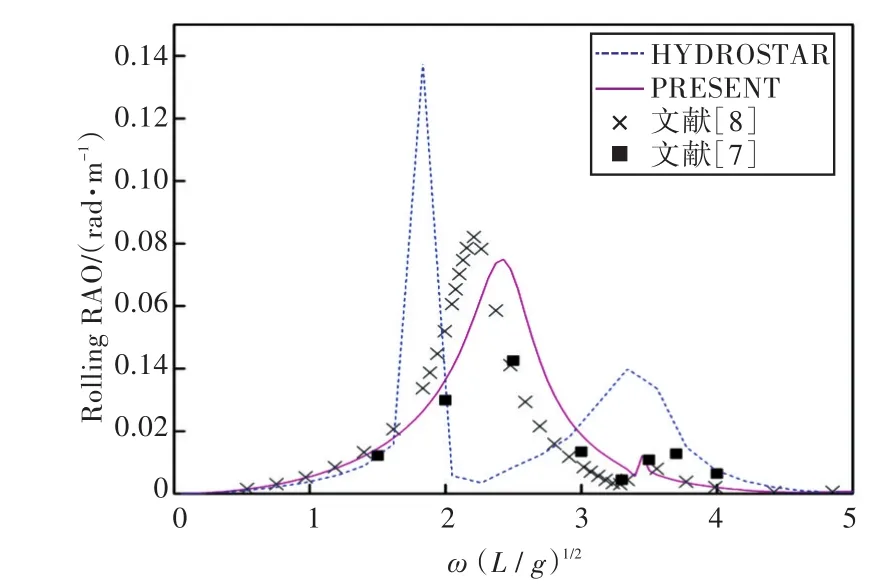
图29 90°浪向下横摇运动响应(前、后舱装载率为30%,30%)Fig.29 Rolling RAO in 90°wave direction angle(filling ratio of fore and back tank is 30%,30%)

图30 90°浪向下垂荡运动响应(前、后舱装载率为30%,30%)Fig.30 Heaving RAO in 90°wave direction angle(filling ratio of fore and back tank is 30%,30%)
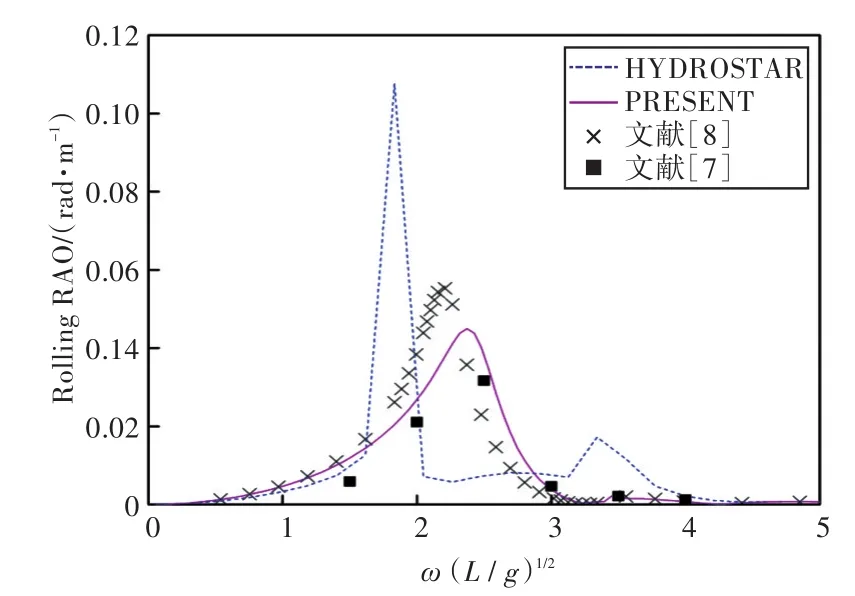
图31 120°浪向下横摇运动响应(前、后舱装载率为30%,30%)Fig.31 Rolling RAO in 120°wave direction angle(filling ratio of fore and back tank is 30%,30%)
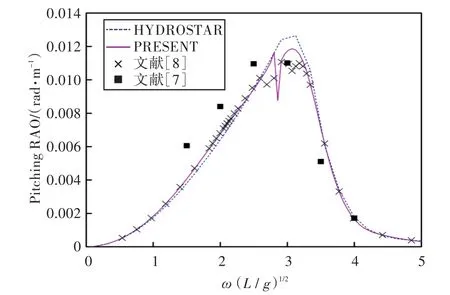
图32 120°浪向下纵摇运动响应(前、后舱装载率为30%,30%)Fig.32 Pitching RAO in 120°wave direction angle(filling ratio of fore and back tank is 30%,30%)
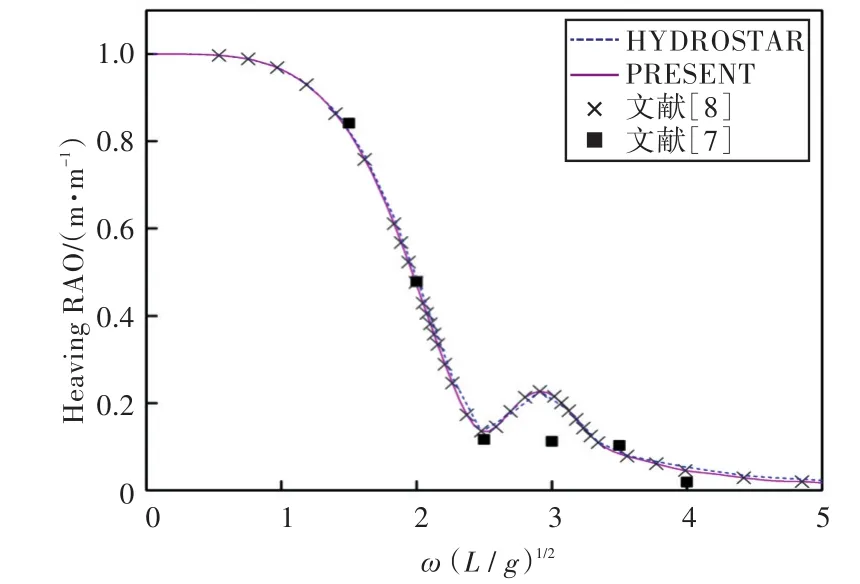
图33 180°浪向下垂荡运动响应(前、后舱装载率为30%,30%)Fig.33 Heaving RAO in 180°wave direction angle(filling ratio of fore and back tank is 30%,30%)
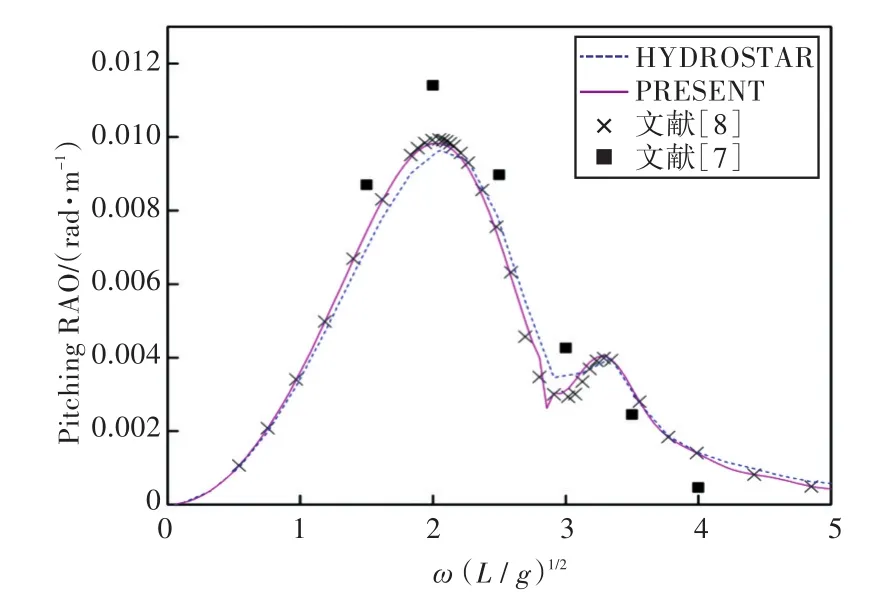
图34 180°浪向下纵摇运动响应(前、后舱装载率为30%,30%)Fig.34 Pitching RAO in 180°wave direction angle(filling ratio of fore and back tank is 30%,30%)
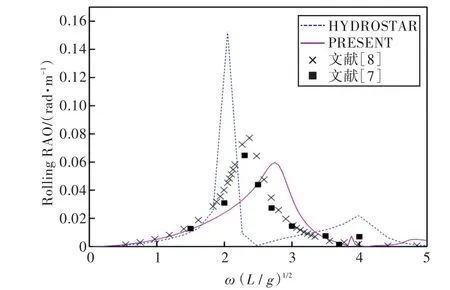
图35 90°浪向下横摇运动响应(前、后舱装载率为57.5%,43.3%)Fig.35 Rolling RAO in 90°wave direction angle(filling ratio of fore and back tank is 57.5%,43.3%)
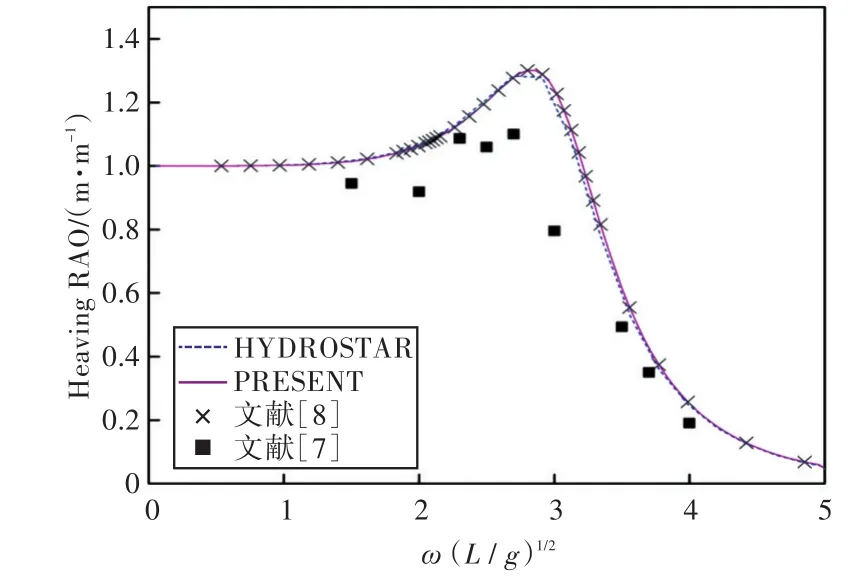
图36 90°浪向下垂荡运动响应(前、后舱装载率为57.5%,43.3%)Fig.36 Heaving RAO in 90°wave direction angle(filling ratio of fore and back tank is 57.5%,43.3%)

图37 120°浪向下横摇运动响应(前、后舱装载率为57.5%,43.3%)Fig.37 Rolling RAO in 120°wave direction angle(filling ratio of fore and back tank is 57.5%,43.3%)
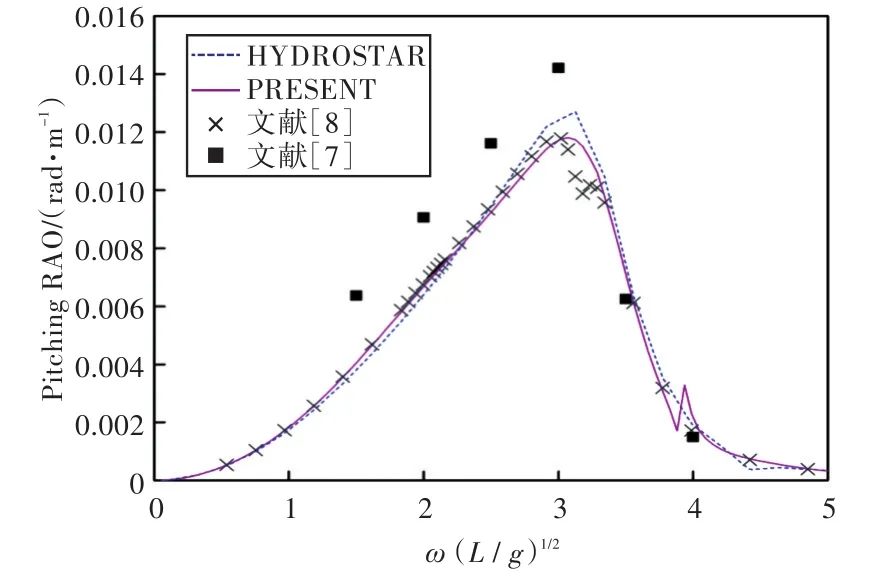
图38 120°浪向下纵摇运动响应(前、后舱装载率为57.5%,43.3%)Fig.38 Pitching RAO in 120°wave direction angle(filling ratio of fore and back tank is 57.5%,43.3%)

图39 180°浪向下垂荡运动响应(前、后舱装载率为57.5%,43.3%)Fig.39 Heaving RAO in 180°wave direction angle(filling ratio of fore and back tank is 57.5%,43.3%)
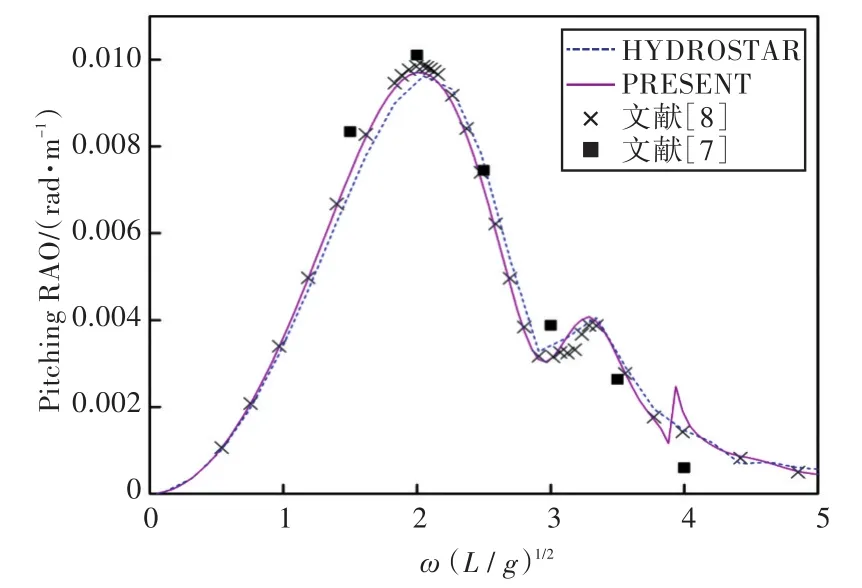
图40 180°浪向下纵摇运动响应(前、后舱装载率为57.5%,43.3%)Fig.40 Pitching RAO in 180°wave direction angle(filling ratio of fore and back tank is 57.5%,43.3%)
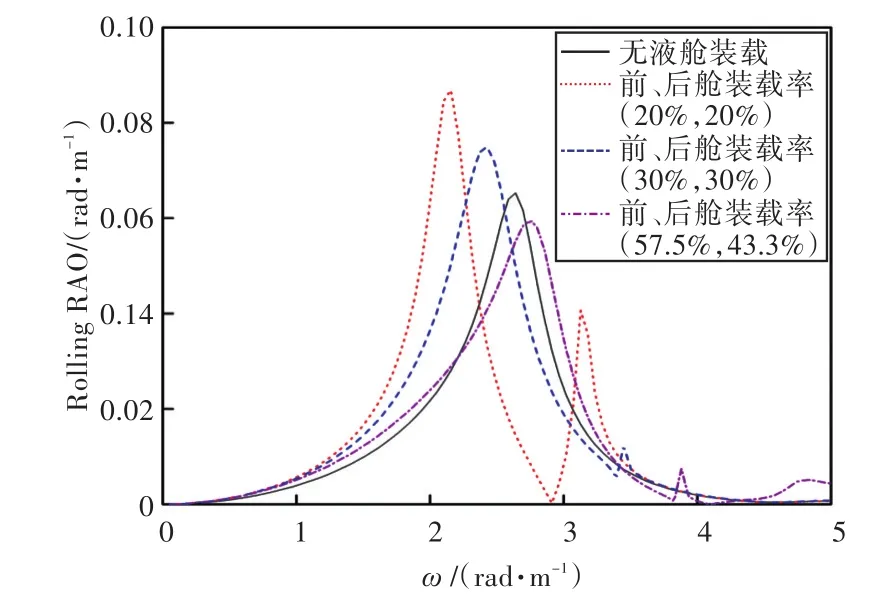
图41 90°浪向下液舱不同装载率下的横摇运动响应Fig.41 Rolling RAO with different filling ratio in 90°wave direction angle
由以上图中对比可以看出:
1)在船舶纵摇和垂荡运动响应方面,以上4种计算结果均吻合较好,而在计算船舶横摇运动响应时,幅值结果和共振频率结果误差较大。这主要是因为船舶纵、横向尺寸比较大,因而在横浪作用下横摇运动较为剧烈。
2)当计算船舶横摇运动响应时,在船舶和液舱共振频率处,采用HYDROSTAR软件计算的结果其幅值与其他计算结果相差较大,这可能是因为采用HYDROSTAR软件计算的没有考虑自由水面阻尼因素;而本文通过增加自由水面阻尼值,船舶横摇运动响应和纵摇运动响应等计算结果均与实验数据以及文献[7]的数值计算结果吻合较好,这也证实了本文计算方法的正确性。
3)由上分析可知,船舶在横浪(90°浪向)下的横摇运动响应较剧烈。因此,通过对比横浪作用下船舶在不同液舱装载率情况下的横摇运动响应可以发现,船舶的共振频率出现了偏移,且当装载率较低时,船舶的共振频率偏于低频,并随装载率的上升而向高频方向移动。当液舱装载液体时,船舶的横摇运动出现了多个峰值,且当前、后液舱装载率为(20%,20%)时,第2个峰值最大,说明此时液舱内流体晃荡得最为剧烈;当装载率高于或者低于此时的装载率时,峰值又降低,说明液舱对船舶运动的影响存在一个“最佳”装载率,在该装载率下,液舱内的流体晃荡对于船舶运动响应最大,在船舶设计时需着重予以注意。
3 结 语
本文通过频域计算方法,对船舶在不同液舱液体装载率情况下的运动响应进行了计算分析。首先,将本文计算结果与其他水动力软件计算结果进行对比,验证了本文计算船舶水动力系数程序的准确性。然后,计算了船舶耦合液舱晃荡作用时的运动响应,将本文计算结果与实验数据及已发表文献的数值结果进行了对比,并采用HYDROSTAR软件进行了计算。通过对比以上计算结果,证实了本文计算方法的正确性,并对结果数据进行了分析,指出了液舱晃荡对船舶所造成的影响。本文所做研究对在船舶设计时需考虑液舱晃荡的影响具有一定的参考意义。

