艇桨一体的螺旋桨激振力和水动力噪声数值预报

王诗洋，汤佳敏，王文全，张祥瑞

1中国船舶及海洋工程设计研究院，上海200011

2哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001

0 引 言

随着科学技术的发展，潜艇的综合作战性能得到了极大提升，但是反潜探测技术的进步也使得潜艇的水下隐蔽性受到空前的挑战［1］。按照噪声等级，可以将潜艇划分为高噪声、低噪声和安静型等不同类别［2］，其中“安静型”潜艇备受青睐。为了提高其生存性和作战能力，噪声控制已成为潜艇总体设计的关键技术。潜艇噪声分为机械振动噪声、螺旋桨噪声以及流噪声［3］，目前，机械振动噪声已通过基座弹性安装、消声瓦隔音处理等降噪技术得到有效控制［4］，螺旋桨噪声在辐射噪声中的占比较大，水动力噪声则对潜艇的自噪声影响较为明显，因此开展艇桨一体的螺旋桨激振力和水动力噪声预报研究具有重要的工程价值。

目前，主要通过实验测量和理论预报这2种方法开展潜艇流噪声方面的研究。毕毅等［5］通过拖曳试验测量了潜艇流噪声并发现了螺旋桨的信号频率特性，尤其是低频线谱特性。杨琼方等［6］采用大涡模拟（Large Eddy Simulation，LES）方法与声学边界元相结合，实现了潜艇流噪声及其等效声中心的数值预报。在螺旋桨噪声的产生机理和特性等方面，Seol等［7-8］基于面元法和噪声分析法，计算了非均匀来流时螺旋桨的空泡和无空泡噪声，分析了不同频率下螺旋桨的声指向性分布情况；Testa等［9］采用边界元方法求解了螺旋桨的表面脉动压力，并采用求解伯努利及FW-H方程的方法预报了远场声压。近年来，数值模拟预报方法日益成熟，结合计算流体力学（CFD）方法和计算声学软件来预报螺旋桨噪声已成为现实。王超等［10］通过耦合LES和声学无限元方法，预报了均匀流螺旋桨的频域噪声。黄胜等［11］采用LES方法计算分析了带螺旋桨的潜艇流场特性，以及螺旋桨对流场噪声的影响。

目前，水动力噪声的研究对象多为裸艇和单桨，工况过于简单，且与实际艇、桨之间的相互耦合作用存在一定偏差。同时，对于艇桨一体的螺旋桨水动力噪声研究而言，鲜有螺旋桨诱导激振力方面的研究成果。为此，本文拟基于LES方法对艇桨一体的流场进行仿真计算，分析潜艇非均匀伴流场中螺旋桨轴承力的时域和频域变化规律，并结合ACTRAN声学计算软件对艇桨水动力噪声性能进行预报，分析声场的声压分布和特征点声压变化曲线，用以为艇桨一体的螺旋桨设计提供参考建议。

1 数学基础

1.1 流体控制方程

流体的流动受物理守恒定律的支配控制，主要包括质量守恒定律、动量守恒定律和能量守恒定律等。由于水介质为不可压缩流体，其热交换能量很小，故可忽略不计，只需基于质量守恒方程和动量守恒方程进行求解即可，其详细计算公式可参考文献［12］。

1.2 LES模型

本文将采用LES方法来模拟湍流流动，其基本思想是通过纳维—斯托克斯（Navier-Stokes，N-S）方程直接模拟大尺度涡，并近似模拟小尺度涡对大尺度涡的影响。首先，建立一种滤波函数，在湍流瞬时运动方程中将尺度比滤波函数小的涡滤除，分解出描述大涡流场的运动方程；然后，通过构建亚格子尺度模型，并引入附加应力项来表示滤除的小涡对大涡流场的影响。

滤波函数G(x，x′)为

式中：V为控制体积所占的几何空间；x为滤波后大尺度涡区域的空间坐标；x′为实际流动区域的空间坐标。

连续性方程为

滤波后的N-S方程为

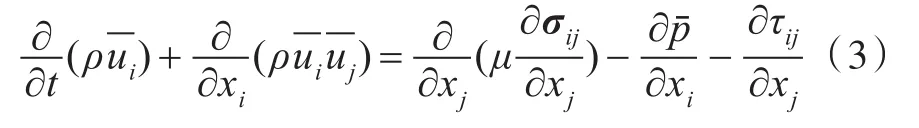
式中：ρ为流体密度；t为时间；xi和为三维笛卡尔坐标系下的方向坐标；ui和uj为流体在xi和xj方向的平均速度；μ为流体的动力粘性系数；σij为由分子粘性引起的应力张量；p为流体微元体上的压力；τij为亚格子尺度应力，表示小尺度涡对所求解运动方程的影响，本文将采用Smagorinsky-Lilly模型来描述亚格子尺度应力；上划线符号“—”表示该项经过了滤波。

1.3 Lighthill声类比理论

基于N-S方程可以推导出Lighthill声类比方程，但其非线性和流—声耦合性使得方程不易求解。为简化计算，将声场分为近场声源区和远场辐射区，并假定辐射区的流动对声场没有影响［13］。在该假定条件下整理简化连续方程和动量方程，即可得到Lighthill声类比方程：

式中：c0为等熵条件下的声速值；ρ'=ρ-ρ0，为噪声扰动时的密度分量，其中ρ和ρ0分别为扰动与未扰动时的流体密度；Tij为Lighthill应力张量。

其中

式中：δij为弹性常量；p'=p-p0为声压，其中p和p0分别为扰动与未扰动时的流体微元体压力。

1.4 基于ACTRAN软件的水动力噪声预报流程

采用ACTRAN软件进行水动力噪声预报时，CFD流场计算与声学计算是解耦的。结合无限元方法，不仅可以考虑偶极子噪声，也可以考虑由湍流引起的四极子噪声。具体计算步骤为（图1）：首先，取声源面周围的一块流动区域作为发声体；然后，通过CFD计算获得该湍流区域的准确流场信息；最后，通过Lighthill声类比方法提取噪声源，进而模拟声场。

图1 流—声耦合计算流程图Fig.1 Flow chart of flow-acoustic coupling calculation

2 计算模型

2.1 计算对象

本文以美国DARPA潜艇模型SUBOFF作为研究对象（图2），其主要参数如表1所示。

选用ITTC推进委员会提供的模型桨DTMB 4383（图3），其侧斜角度为 72°，具体几何参数如表2所示。表中：d为螺旋桨毂径；AE为螺旋桨各叶伸张轮廓所包含的面积之和；AO为螺旋桨盘面积，即螺旋桨梢圆面积。

图2 SUBOFF潜艇模型Fig.2 SUBOFF model

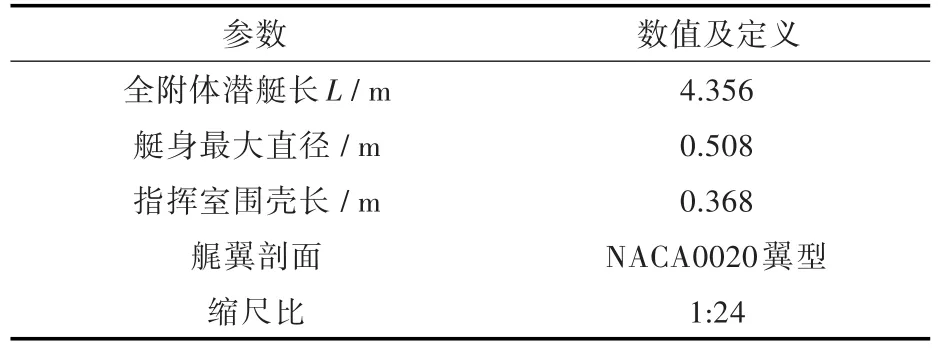
表1 SUBOFF潜艇模型主要参数Table 1 Main parameters of SUBOFF model

图3 DTMB 4383桨模型Fig.3 Model of DTMB 4383 propeller

表2 DTMB 4383主要参数Table 2 Main parameters of DTMB 4383

2.2 网格划分

2.2.1 流场计算网格划分

带桨潜艇的流场计算域模型如图4所示。其中，进流面距艇艏1倍艇长，尾流出口距离艇艉2倍艇长，流场的径向直径为10倍艇身最大直径，即5.08 m。潜艇表面网格划分分为2块（图5），螺旋桨等小域采用非结构化网格，对边界层进行局部加密，其余部分则采用结构化网格。

图4 带桨潜艇的计算域Fig.4 Computational domain of submarine with propeller

图5 潜艇表面网格Fig.5 Submarine surface mesh

2.2.2 声学计算网格划分

声学网格包括声源面、声源区及声传播区。声源面即发声面，是潜艇的表面网格，代表了偶极子声源。声源区即潜艇表面周围的湍流流动区域体网格，代表了四极子声源，其中声源区的选取范围应小于CFD计算中潜艇所影响的流场范围。同时，在体声源之外还要选取一层代表无限元边界面的圆柱面，即声传播区，其界面范围没有上限，视计算需要而定。本文建立的声学计算结构模型如图6所示，其中无限元界面两端与潜艇艏、艉的距离均为1倍艇长，即1L，圆柱半径则为1.5L。

图6 带桨潜艇的声学计算域Fig.6 Acoustic computational domain of submarine with propeller

与流场大涡模拟计算相比，声场计算对网格质量的要求相对较低。鉴于计算精度和时效性要求，声学网格的尺寸仅需满足每个波长至少分布6个网格节点即可。因此，利用网格生成软件ICEM进行非结构网格划分的声学网格如图7所示，声场监测点布置如图8所示。

2.3 流场计算边界条件

图7 声学网格Fig.7 Acoustics mesh

图8 潜艇声场监测点布置图Fig.8 Arrangement plan of submarine sound field monitoring point

将流域入口和出口分别设为速度入口和压力出口，来流速度设为v0=3.05 m/s，周向壁面设置为Symmetry，旋转域与流场大域的交界面设置为Interface。采用滑移网格技术实现螺旋桨的旋转效果，螺旋桨转速设为n0=515 r/min。采用SIMPLEC方法进行压力速度耦合迭代，时间步长设置为0.000 25 s；采用大涡模拟方法对流场进行非定常计算。

3 计算结果分析

3.1 螺旋桨激振力计算结果

螺旋桨在艇体艉部的不均匀流场中工作时必然会产生激振力，包括轴承力和艇体表面的脉动压力。剧烈的激振力将导致艇体艉振，影响轴承强度和艇桨水动力噪声，故激振力控制是低噪声螺旋桨的一项关键技术。由于潜艇螺旋桨距离艇体较远，其对艇体表面脉动压力的影响比水面舰船弱，故在进行声学计算之前，仅需针对螺旋桨轴承力开展分析。在螺旋桨激振力中，一阶叶频的占比较大，倍叶频和高阶谐波分量的占比较小，且随阶数的增加而迅速衰减，因此在螺旋桨激振力计算结果中只有叶频分量。

待计算收敛稳定后，记录约3.5个周期（4～4.4 s）的激振力时域数据，并通过快速傅里叶变换求得频谱曲线。图9、图10所示为螺旋桨激振力和激振力矩的时域与频域曲线。从时域图中可以看出，螺旋桨激振力和激振力矩随着时间的推移而周期性变化；从频域图中可以看出，螺旋桨激振力和激振力矩具有相同的脉动频率，在叶频（Blade Passing Frequency，BPF）（42.9 Hz）整数倍处均呈现不同幅值的尖峰，其中1倍叶频处的峰值最大，然后迅速衰减为0。通过对比螺旋桨的3种激振力可知，其水平力脉动最大，垂直力脉动次之，而推力脉动最小，螺旋桨激振力矩的变化规律与之相似。这主要是由非均匀流场中螺旋桨叶片受力不均衡所致，尽管垂直力和水平力的幅值不高，却产生了较大的脉动分量，这与文献［14］中的结论一致。如果垂直力和水平力的脉动分量过大，将导致轴系和艇体在水平方向与垂直方向的结构振动，这一点应特别注意。

图9 螺旋桨激振力脉动的时域与频域曲线Fig.9 The time domain and frequency domain curves of propeller excitation force fluctuation

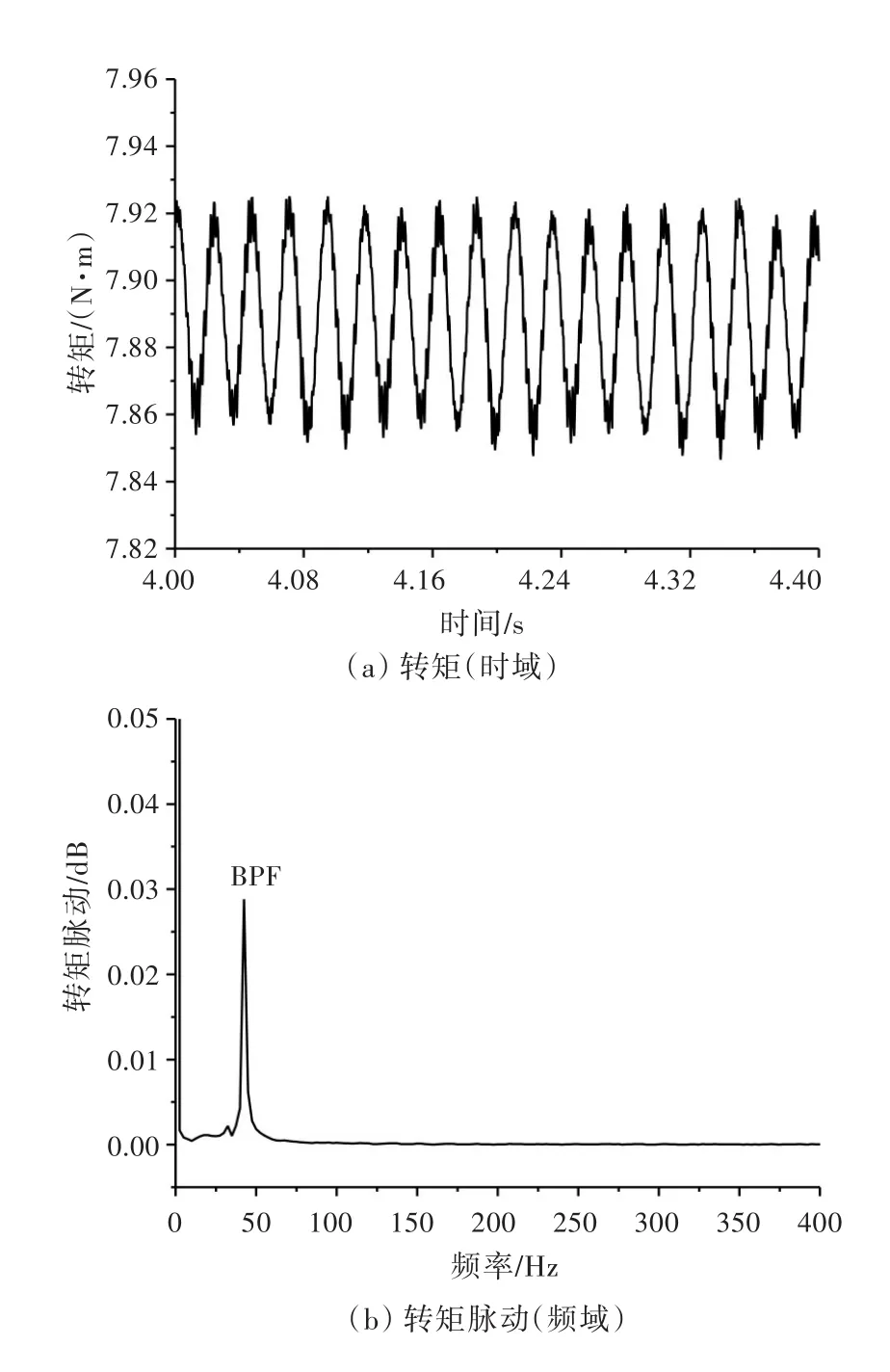
图10 螺旋桨激振力矩脉动的时域与频域曲线Fig.10 The time domain and frequency domain curves of propeller excitation torque fluctuation

3.2 艇桨一体的流场计算结果

本节将计算潜艇表面的压力分布，并与全附体潜艇的试验值进行对比，用以分析螺旋桨对潜艇表面压力场的影响。对单片桨叶而言，非均匀伴流场对螺旋桨水动力系数的影响较明显，在一个旋转周期内表现出了稳定的规律性；对整个螺旋桨而言，其推力和转矩系数约为单片桨叶的5倍，即等于螺旋桨的桨叶数量［11］。

图11所示为潜艇中纵剖面脊线上各监测点的压力系数分布，其中CP为无量纲压力系数，x为各监测点到艇艏的距离。由图可知，安装螺旋桨之后，艇体表面的整体压力分布变化不大，但指挥室围壳前端附近的压力波谷幅值变小，艉翼前端附近的波谷幅值变大，且艉翼后方的压力幅值急剧变小。由此可见，螺旋桨对潜艇艉部压力分布的影响较大，其中螺旋桨附近的艇体表面出现了压力骤降，这是由于螺旋桨的抽吸作用使得叶片背侧的压力转为吸力所致。

图11 潜艇中纵剖面脊线上的压力系数分布Fig.11 Pressure coefficient distribution in central longitudinal section ridge line of submarine

图12所示为潜艇中纵剖面的轴向速度分布。从图中可以看出，指挥室围壳和艉翼后方均出现了不同程度的低速区，这说明附体对流场的影响较为明显。同时，螺旋桨四周的流速较大，桨轴正后方的流速最低，这与螺旋桨的流场特性完全吻合。

图12 潜艇中纵剖面的轴向速度分布Fig.12 The axial velocity distribution of submarine central longitudinal section

图13所示为潜艇表面压力分布。从图中可以看出，潜艇最前端、指挥室围壳、艉翼前端和螺旋桨叶稍部位均存在局部高压区，所以这4个位置可能是噪声的主要贡献点。

图13 潜艇表面的压力分布Fig.13 Pressure distribution of submarine surface

3.3 艇桨一体的水动力噪声计算结果

3.3.1 艇桨一体的声场声压云图

图14所示为艇桨一体的声场声压云图。由图可知，指挥室围壳、艉翼和螺旋桨附近的声压级明显较高，且不同频率下的声压分布云图差别较大。在低频工况下，只有潜艇艏部和艉部存在明显压差，声辐射区间呈圆形分布。随着频率的增加，声辐射区间开始呈瓣状分布，且瓣状区间逐渐增加（970 Hz时有4个，1 380 Hz时有5个）；此时，潜艇附体和螺旋桨附近存在明显的局部高压区，这表明附体和螺旋桨对流场噪声的影响很大，与3.2节的结论一致。总体而言，随着频率的增加，辐射声压将呈现出更为明显的“蝶形”瓣状分布和更多的波峰，这一现象与文献［15］的计算结果基本一致。由图14可知，声压分布相对于潜艇中轴线具有较好的对称性，仅在少数频率下存在小角度偏转现象。

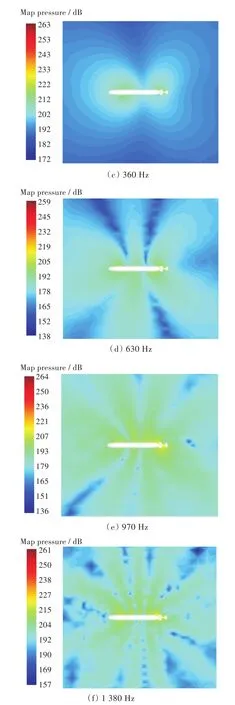
图14 潜艇水平剖面声压云图Fig.14 The sound pressure contours of submarine horizontal section

3.3.2 特征点的声压频谱特性

螺旋桨噪声一般有如下特性：主要集中在低频段，低频离散噪声远大于高频噪声，且0～200 Hz频段的噪声衰减速度明显高于其他频段；在远离桨盘面中心相同距离的不同位置处，径向的声压级高于轴向；随着远离桨盘中心，噪声总声压级将逐渐减小，其衰减速度不断减小［16］。

为了进一步分析螺旋桨的声压特性，本文选取了2个特征监测点，即潜艇正下方2 m处（特征点P1）和潜艇艏部正后方6 m处（特征点P2），其声压频谱曲线分别如图15和图16所示。由图可知，带桨潜艇的水动力噪声主要集中在低频段。随着频率的增加，声压级（Sound Pressure Level，SPL）有所降低，其波动范围逐渐趋于稳定。经计算，P1点的总声压级为212.86 dB，P2点的总声压级为218.93 dB，其中潜艇正下方的声压值约比全附体潜艇高100 dB，而螺旋桨正后方的声压值约比全附体潜艇高130 dB。由此可见，安装螺旋桨之后，潜艇辐射声场声压值变化较大，其中以螺旋桨正后方的影响最为明显。

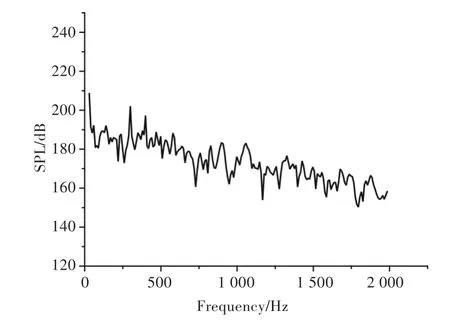
图15 P1处的声压频谱曲线Fig.15 Sound pressure spectrum curve at P1

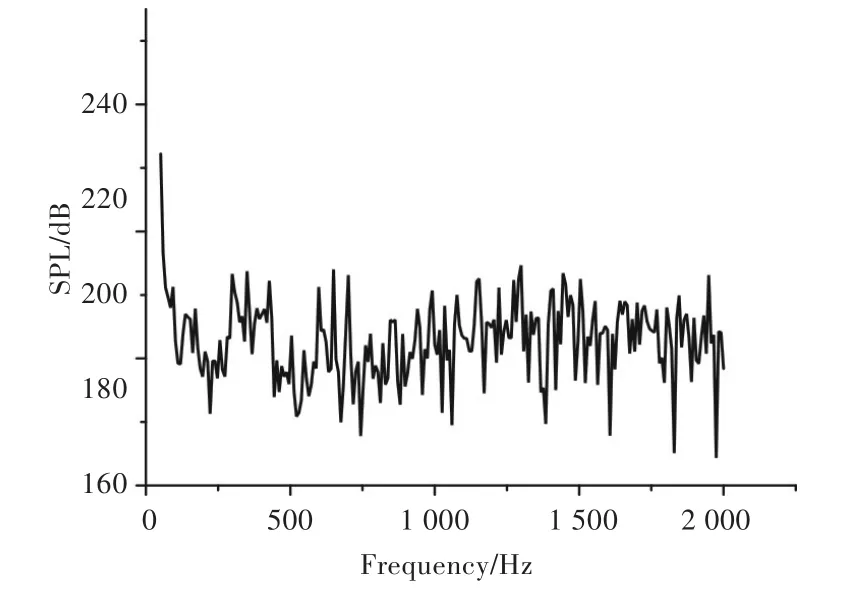
图16 P2处的声压频谱曲线Fig.16 Sound pressure spectrum curve at P2

3.3.3 艇桨一体的声指向性

为了深入研究带桨潜艇的辐射噪声特性，本文将基于沿潜艇圆周均匀布置的各监测点声压值，具体分析潜艇水下辐射噪声的指向特性。鉴于上文已针对潜艇水平剖面声压云图开展了全面分析，故此处仅选取潜艇正后方沿轴向布置的各监测点声压值来分析垂直方向上的声指向特性。一般螺旋桨的轴向声压等级明显低于径向，声指向性呈“3”字形分布；若在整个圆周均匀布置监测点，则声指向性将呈“8”字形分布［16］。由文献［16］可知，螺旋桨辐射噪声指向性关于50°角的方向呈对称性分布，但上、下两侧的分布极不对称，这可能是由于非均匀来流与叶片之间的耦合作用所致［16］。

图17所示为潜艇正后方的垂向声指向性示意图，为了更清晰地展示声指向规律，本文将各监测点的总声级均减去了一个基数（180 dB）。由图可知，在潜艇后方的横剖面上，声指向性大致呈圆形分布，各点处的声压级差值较小，仅潜艇正上、正下2个点的声压级略高。这与不带桨潜艇的垂直指向性规律差别较大，这是由于螺旋桨旋转时改变了周围流场，从而削弱了艉翼对潜艇后方声压分布的影响。

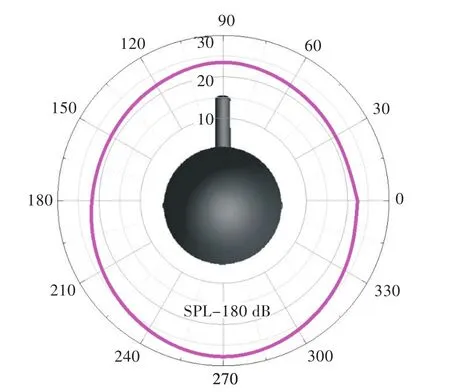
图17 潜艇正后方的声指向性（垂向）Fig.17 Sound directivity behind the submarine（vertical）

4 结 论

本文以SUBOFF潜艇和DTMB 4383桨为计算对象，首先分析了艇桨一体的螺旋桨激振力和潜艇流场，然后基于ACTRAN软件计算了艇桨一体的水动力噪声，得到如下结论：

1）螺旋桨激振力的各个分量具有相同的脉动频率，在叶频整数倍处呈现不同幅值的尖峰，其中1倍叶频处的峰值最大，然后迅速衰减为0。

2）对于螺旋桨的3种激振力，水平力脉动最大，垂直力脉动次之，推力脉动最小，螺旋桨激振力矩的变化规律与之相似。

3）潜艇指挥室围壳、艉翼和螺旋桨对其流场速度分布的影响较大，其中潜艇最前端、指挥室围壳、艉翼及螺旋桨叶梢部位均存在局部高压区，这是水动力噪声的主要贡献点。

4）潜艇水平声压分布相对于潜艇中轴线具有较好的对称性。随着频率的增加，潜艇辐射声压将呈现出更为明显的蝶形分布和更多的波峰。

5）根据特征监测点的频谱曲线，发现带桨潜艇的水动力噪声主要集中在低频段，随着频率的增加，声压级有所降低。此外，与无桨全附体潜艇相比，艇桨一体的辐射声场声压值变化较大，其中螺旋桨正后方的影响最为明显。

目前，本文仅针对缩比模型尺寸下艇桨一体的螺旋桨激振力和水动力噪声进行了初步预报，后续将开展实尺度条件下的深入研究工作，并将对比分析潜艇尺度效应带来的一系列影响。