后燃烧效应对约束空间内爆炸载荷的影响规律

徐维铮 ，吴卫国

1武汉理工大学高性能舰船技术教育部重点实验室，湖北武汉430063

2武汉理工大学交通学院，湖北武汉430063

0 引言

针对约束空间内的爆炸问题，爆炸后燃烧效应是需要重点关注的内爆炸物理现象。大多数炸药（TNT炸药、温压炸药、SDF混合型炸药［1］等）的爆轰产物具有负氧性，高温高压爆轰产物在膨胀过程中会与周围空气中的氧气进行剧烈的燃烧反应并释放大量能量，这一物理现象为后燃烧效应［2］。后燃烧效应对爆炸冲击波的传播过程、冲击波壁面反射压力、准静态压力都会产生一定的影响。

为了研究约束空间内后燃烧效应对爆炸载荷的影响规律，国内外学者开展了大量的实验和数值模拟研究。金朋刚等［3］采用压力传感器测量了在密闭罐体内分别存在氮气、空气和氧气3种条件下TNT炸药在后燃烧过程中产生的准静态压力，结果表明，在氧气环境下，TNT炸药的后燃烧效应较明显，能够产生更大的准静态压力。李鸿宾等［4］在容积为500 L的密闭爆炸罐中进行了TNT炸药爆炸实验，发现随着环境中氧气量的增大，准静态压力增大，说明提高环境中的氧气含量能够提高爆轰产物的反应率。李芝绒等［5］通过实验测量了在圆柱形密闭爆炸罐内分别存在空气和氮气这2种条件下温压炸药爆炸的冲击波峰值以及罐体内的准静态压力，结果表明，在爆轰反应阶段，氧气与超细铝粉发生氧化反应，空气环境中的冲击波峰值和冲量比氮气环境的略高；在后燃烧阶段，氧气与铝粉混合产生后燃烧反应，释放出大量的热量，与氮气环境相比，空气环境中的准静态压力和热响应温度峰值显著增大。Kuhl等［6］提出采用多流体模型描述考虑后燃烧效应的爆炸场，将爆炸组分划分为燃料、空气和产物3种成分，分别对这3种成分建立质量、动量、能量守恒方程，在爆炸过程中，采用狄拉克函数进行燃烧阵面的捕捉，释放后燃烧能量，并开发了网格自适应数值计算程序。Togashi等［7-8］将自主开发的三维爆炸波数值计算程序与劳伦斯利弗莫尔实验室开发的Cheetah编码衔接，利用Cheetah编码计算后燃烧能量，再将后燃烧能量添加到自主开发的程序，实现爆炸过程中后燃烧效应的模拟。

爆炸流场包含高密度比和高压力比强间断等复杂流场结构，对爆炸过程进行数值模拟时，需要高精度、强稳定性激波捕捉格式。Liu等［9］提出了加权本质无振荡格式（Weighted Essentially Non-Oscillation Scheme，WENO），Jiang等［10-11］发展了该格式并扩展了其应用。目前，WENO格式作为一种典型的高精度激波捕捉格式，对流场内的激波间断具有较高的分辨率，适用于求解包含激波、膨胀波以及接触间断等复杂结构的流场。

由于后燃烧过程涉及复杂的多组分燃烧化学反应，如果考虑详细的化学反应过程，不仅程序编写复杂，且由于化学反应时间尺度与流场时间尺度存在差别，计算量大，难以应用于实际工程问题计算中。为此，本文拟提出一种考虑后燃烧效应的简化反应率模型，考虑到WENO格式精度高及稳定性较好的优势，基于Fortran平台，采用五阶WENO有限差分格式，自主开发约束空间内考虑爆炸后燃烧效应的二维数值计算程序，并探讨反应速率及后燃烧能量大小对约束空间内爆炸载荷的影响规律。

1 控制方程及数值求解

为了近似考虑爆炸后燃烧效应，在Miller反应率模型［12］思想的启发下，提出一种考虑炸药爆炸后燃烧效应的数值计算方法，初步探讨后燃烧效应对约束空间内爆炸载荷的影响规律。

Miller反应率模型最初提出的目的是近似描述含铝炸药爆轰过程中铝粒子在爆轰波阵面后的反应过程［12］。我们尝试将模型思想推广应用到约束空间内爆炸后燃烧效应的数值计算中。本文采用的反应率模型如下：

式中：a为反应速率常数；p为流体压力；α为后燃烧过程中反应率（初始时α=1，反应完成后α=0）。

不考虑后燃烧效应的可压缩欧拉方程为

其中，

将反应率模型式（1）耦合到式（2）中，并以源项的形式进行后燃烧能量的添加，可得考虑后燃烧效应的可压缩欧拉方程为

其中，

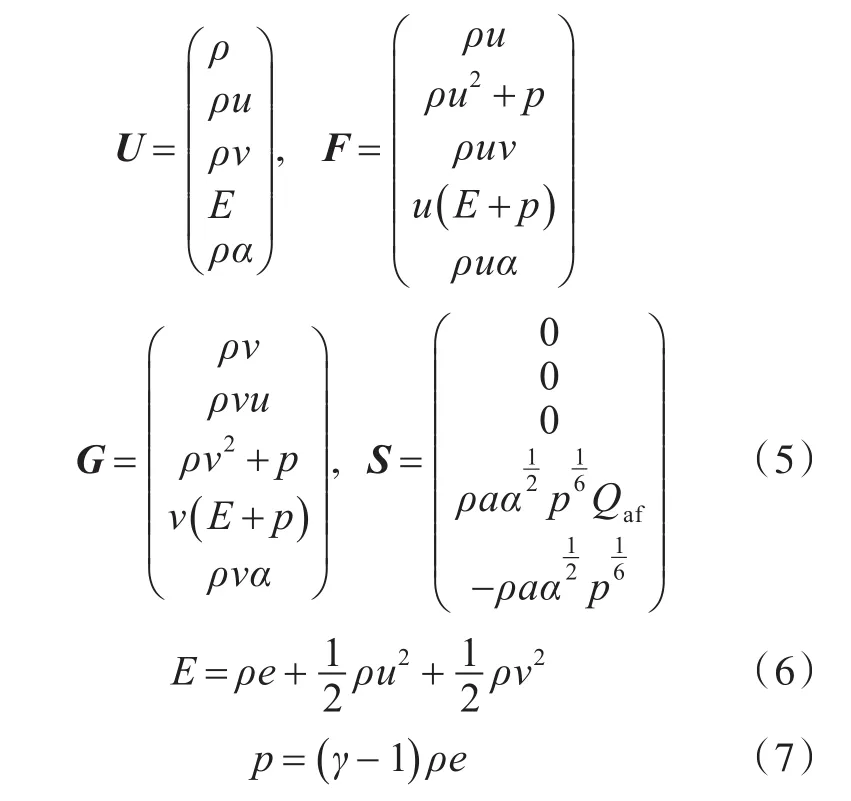
以上式中：ρ为密度；u，v分别为x，y方向上的速度分量；E为单位体积流体的总能量；e为比内能；Qaf为爆炸后燃烧过程中单位质量释放的能量，J/kg；γ为气体的绝热指数，文中γ统一取为1.4。

式（5）在每个方向上均可以看成是一个带有源项的双曲守恒律方程：

例如，针对x方向，式（8）的半离散守恒型格式为

2 约束空间内爆炸后燃烧效应数值计算

采用五阶WENO有限差分格式，自主开发了约束空间内考虑爆炸后燃烧效应的二维数值计算程序。自主程序对于爆炸波的数值计算可靠性在文献［14-15］中已经得到验证。本节采用自主程序对约束空间内炸药爆炸过程进行数值模拟研究，主要探讨反应率演化过程及后燃烧能量的加入对爆炸载荷的影响规律。

2.1 舱室尺寸及测点布置

长方形舱室的尺寸如图1（a）所示，图中数值单位为mm。在舱室壁面上设置了3个典型测点，用于监测爆炸载荷时间历程和反应率时间历程。均匀网格步长取为10 mm，如图1（b）所示。

图1 舱室尺寸及网格划分Fig.1 Size of cabin and mesh partition

2.2 初始条件和边界条件

基于瞬时爆轰假定，将方形炸药等效为均匀高压气团，具体参数为：边长22.2 mm，密度1 630 kg/m3，压力 3.057 9×109Pa。炸药设置在舱室中间，即图2（a）中的红色区域，周围蓝色区域为空气域，空气密度为1.0 kg/m3，压力为1.0×105Pa。初始时刻反应率分布见图2（b）中的红色区域。初始时刻反应还没发生，炸药所在区域反应率为1，舱室其他区域反应率为0。壁面边界条件设置为刚性边界，由于冲击波与结构变形耦合效应十分复杂，这里暂时不考虑舱室结构的变形。

2.3 计算工况

图2 爆炸初始条件Fig.2 Initial condition for the explosion

为了探讨反应速率和后燃烧能量大小对爆炸过程的影响规律，选取2类典型工况进行计算。工况1：后燃烧单位质量释放的能量Qaf=4.69×106J/kg，保持其他参数不变，反应速率常数分别取为a=0，10，40。工况2：反应速率常数为a=10，保持其他参数不变，后燃烧单位质量释放的能量分别取为Qaf=0，3.0×106，4.69×106J/kg。

2.4 反应率演化过程分析

为了探讨爆炸后反应率在舱室内部的演化过程，给出了2种工况在不同时刻的反应率分布图，如图3所示，其中左图为a=0，Qaf=4.69×106J/kg；右图为a=10，Qaf=4.69×106J/kg。由图3可知，2种工况下，反应率在不同时刻总体呈现相似的空间分布形态。在爆炸工况a=0，Qaf=4.69×106J/kg中反应速率常数为零，即在整个爆炸过程中没有发生反应，没有后燃烧能量的加入。根据式（4）可知，该工况求解的是爆轰产物质量分数的演化过程；由于爆炸工况a=10，Qaf=4.69×106J/kg中反应速率常数不为零，反应速度快，从而导致舱室内部的反应率快速下降，最终趋近于0。

图3 不同时刻的反应率分布图（左：a=0，Qaf=4.69×106J/kg；右：a=10，Qaf=4.69×106J/kg）Fig.3 Reaction rate distribution at different moments（left：a=0，Qaf=4.69× 106J/kg；right：a=10，Qaf=4.69 × 106J/kg）

为定量显示舱室内部反应率的变化，图4给出了工况1（a=0，10，40；Qaf=4.69×106J/kg）壁面测点1和2的反应率时间历程曲线。由图4可见，随着反应速率常数a的增大，反应率迅速下降，反应完成后，反应率等于0。这里需要说明的是，当反应速率常数a=0时，反应没有发生，根据式（4）可知，反应率的演化过程就是爆轰产物质量分数的演化过程，由于爆炸后爆轰产物与舱室内部的空气进行了复杂的掺混过程，因此舱室内部爆轰产物的质量分数数值将趋近于大于0而小于1。

图4 工况1壁面测点1和2的反应率时间历程曲线Fig.4 Time history curves of reaction rate for gauging points No.1 and No.2 in explosion case one

图5给出了工况2（Qaf=0，3.0×106，4.69×106J/kg；a=10）壁面测点1和2的反应率时间历程曲线。由图5可以看出，在反应速率常数一定的情况下，后燃烧能量的加入对反应速率时间历程的影响显著，然而随着后燃烧能量Qaf的增大，其大小对反应速率时间历程的影响较小。

图5 工况2壁面测点1和2的反应率时间历程曲线Fig.5 Time history curves of reaction rate for gauging points No.1 and No.2 in explosion case two

2.5 后燃烧能量的加入对爆炸载荷的影响

为了探讨不同反应速率常数a对舱室内部爆炸载荷的影响规律，给出了工况1（a=0，10，40;Qaf=4.69×106J/kg）壁面典型测点3的超压时间历程曲线（图6）。由图6可以看出，后燃烧能量的加入明显增强了冲击波载荷和冲量；随着反应速率常数a的增大，冲击波到达时间提前，冲击波峰值增大，冲量增大。由于后燃烧能量的加入，与工况a=0，Qaf=4.69×106J/kg相比，工况a=10，40；Qaf=4.69×106J/kg的准静态超压峰值增大。由于后燃烧能量相同，工况a=10，Qaf=4.69×106J/kg和工况a=40，Qaf=4.69×106J/kg具有相同的准静态超压峰值。

图6 不同反应速率常数下测点3爆炸载荷的时间历程曲线Fig.6 Blast load time histories with different reaction rate constants for gauging point No.3

为了探讨不同后燃烧能量大小Qaf对舱室内部爆炸载荷的影响规律，给出了工况2（Qaf=0，3.0×106，4.69×106；a=10）壁面典型测点 3的超压时间历程曲线（图7）。由图7可以明显看出，在反应速率常数一定的情况下，随着后燃烧能量Qaf的增大，载荷强度增大，最终的准静态超压峰值增大。

为了初步验证本文后燃烧能量加入的可靠性，从准静态超压峰值的角度进行了对比分析。根据文献［16］可知，封闭舱室内部准静态超压峰值的计算公式为

图7 不同后燃烧能量下测点3的爆炸载荷时间历程曲线Fig.7 Blast load time histories with different afterburning energy for gauging point No.3

式中：m为炸药质量；Qtol=QTNT+Qaf，为爆炸过程中释放的总能量，包含后燃烧过程中释放的能量Qaf，其中QTNT=4.69×106J/kg，为炸药的爆热；p0为初始大气压力；V为舱室体积；ρE=1 630 kg/m3，为炸药密度。

将工况1，2中的后燃烧能量Qaf代入式（10），得到准静态超压峰值的理论计算值，再将理论计算结果与数值模拟结果进行对比，结果如图6（a）和图7（a）所示。由图可以明显看出，理论计算结果与数值模拟结果吻合较好，证明了后燃烧能量加入的可靠性。

3 结 论

通过研究得到如下主要结论：

1）在后燃烧能量大小一定的情况下，反应速率常数增大时，冲击波到达时间提前，冲击波峰值、冲量均增大，准静态超压峰值保持不变。

2）在反应速率常数一定的情况下，随着后燃烧能量的增大，冲击波峰值、冲量及准静态超压峰值均增大，后燃烧能量的加入能显著增强爆炸载荷强度。

3）本文针对爆炸后燃烧过程的数值计算，尽管没有考虑复杂的多组分反应过程，然而采用一种简化的反应率模型近似描述后燃烧能量对爆炸载荷的影响，不失为一种满足实际工程计算的有效方法。

本文的研究方法及结果可为进一步研究内爆炸复杂多组分后燃烧效应及抗爆结构设计提供参考和借鉴。