锚杆锚固质量等级快速评级方法研究

王开华，杨森，周继中，曹其壮

（中国水利水电第七工程局有限公司，成都611730）

0 引言

在工程实践中，锚杆支护技术广泛应用于地下洞室、隧道支护工程及高边坡治理工程[1]，其质量的无损检测通常采用声波反射法[2-4]。锚杆质量等级主要分为A、B、C、D 四类[5]，其中A 级和B 级确定为合格，C 级和D 级确定为不合格，其依据如表1 所示。

如表1 所示，规程中仅给出了锚杆锚固密实度和等级的定性判别标准，许多地方用词较为模糊，如“杆底反射信号微弱”、“有较弱的缺陷反射波”、“清晰的杆底反射波”，在实际应用中不容易掌握相应的尺度，而且标准要求同时识别时域信号特征和幅频信号特征，这在一定程度上增加了计算量和识别难度。因此，为了便于计算机程序对锚杆锚固的质量等级进行定量识别，本文严格遵循锚杆密实度质量评判规程，提出了一种基于阈值评级的锚杆锚固质量等级快速评级方法，该方法仅针对锚杆的杆底反射的时域信号进行处理，便能满足分类标准要求，且具有简单、高效、准确的特点。

1 算法概述

1.1 数据预处理

由于锚杆反射信号原始数据存在长度不一致，采样间隔不一致等问题，无法直接用于算法处理，因此在进行分类之前，需对原始数据进行一系列预处理操作，使得用于分类处理的输入数据是经过归一化的可以相互比较的完整数据。而且预处理操作，可提升算法的正确性和分类的准确性。

（1）原始数据归一化以及获取相似度矩阵

原始数据的归一化处理过程包括Y 方向和X 方向的归一化。Y 方向的归一化是振幅归一化，即将反射信号的纵坐标归一化到设定的振幅区间。X 方向的归一化是时间归一化，即将以不同采样间隔获取的原始数据，通过曲线拟合和重采样的方法归一化到同样的采样间隔。归一化的作用是排除激荡信号大小的不同和锚杆长度的不同对后续算法的影响。

表1 锚杆密实度质量等级分类依据

现有仪器会对每根锚杆进行六次不同的测量作为一组数据，个别同组原始数据会含有异常数据，为了排除异常数据的影响，本文采依据公式（1）计算同组数据的两两相似度，并组成相似度矩阵，将比较突出的异常数据筛除。

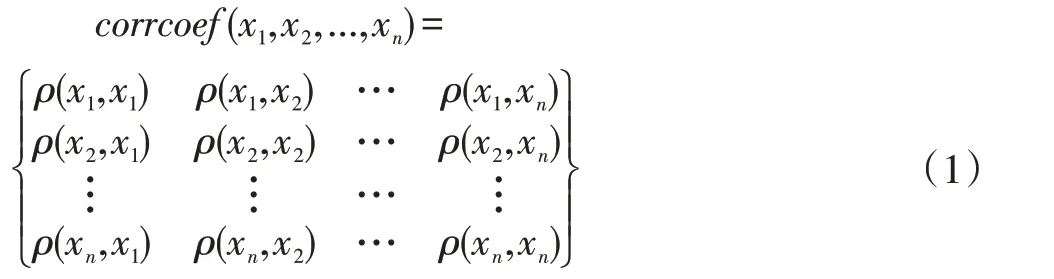
其中xi(x=1,2,…6)表示某根锚杆的六次测量数据，corrcoef(·)表示计算相似度矩阵，ρ(m,n)表示计算m、n 的相似度，本文通过公式（2），计算m、n 的相似度：

其中μm,σm分别是m 的均值和标准差。

在同一根锚杆上采集的数据不应该有较大的差别，任意两组数据的相似度应为0.9 以上。如果某数据与同组的其余数据相似度均不足0.9，那么将该数据视为异常数据排除，保留剩余数据。如果某组中有多于两个异常数据，那么将整组数据视为异常数据排除。

（2）x 方向修正以及上下峰值预处理

本文所述算法需要获取归一化后的曲线x、y 值以及上下峰值分别对应的坐标值，上下峰值即在发射信号的波形图中，正方向的峰值称为上峰值，在负方向的峰值称为下峰值，在后续计算中上下峰值分别计算。

由于现场测量时，激振信号的强度和持续时间的不同，会导致反射信号的主频率或周期不同，从信号的波形图上分辨，则表现在不同测量时，x 方向的峰值间隔不同，如图1 所示，同一个样本1-（14）内的两组数据1-（14）_1 以及1-（14）_4 相比较而言，从视觉上就可以看出曲线1-（14）_1 的峰值间隔与曲线1-（14）_4 的峰值间隔并不相同。为了便于后续计算和比较，需要将其统一到一个基准上进行计算，即进行x 方向上修正。

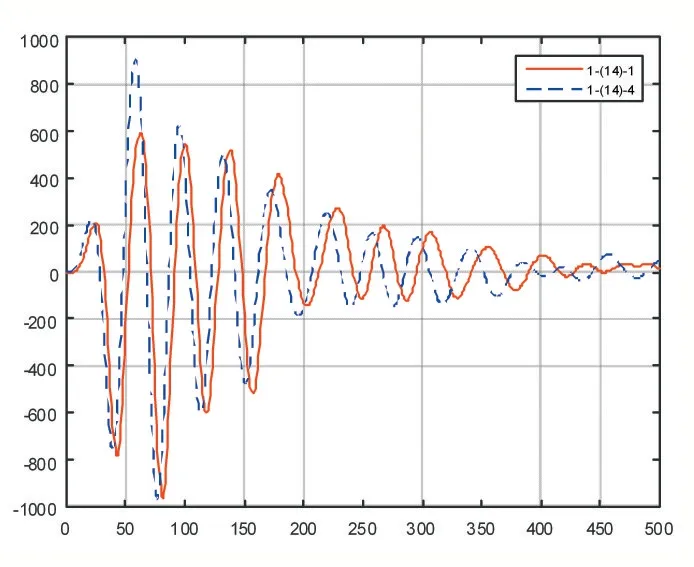
图1 修正之前的样本数据曲线

具体修正过程如下：

①获取曲线的前三个上峰值点p1,p2,p3；

②计算峰值横坐标间隔平均值：

其中，pix表示峰值pi的横坐标，将pavg设置为修正系数；

③对全部点的横坐标值进行修正：

其中，xbefore、xafter分别表示修正前后的横坐标值。

同时，由于激振信号等原因，可能出现第1 个上峰值或下峰值未达到该方向最大的情况，在后续峰值比较时该峰值不具备参考意义，需要去除该峰值，使其不参与后续峰值计数和处理。

1.2 阈值分类方法

在具体分类过程中，由于A、B 类波形曲线比较相似，C、D 类波形曲线比较相似，而AB 类与CD 类相比较而言，波形相差较大，如图2 所示，故采取由粗到精的分组分类策略，先将A、B 类视为一组，C、D 类为一组，完成分组分类后，再依据各类别特征具体分为A、B、C、D 种等级。

首先AB 类波形规整，只在前段有较大起伏，而CD 类波形较散乱，因此可通过曲线后段部分峰值均值作为分类依据。分别获取上下峰值点数组[u1,u2,…,um]和[d1,d2,…,dn]。以上峰值为例，将从ui开始的后续x个峰值点用于计算，下峰值点同理。

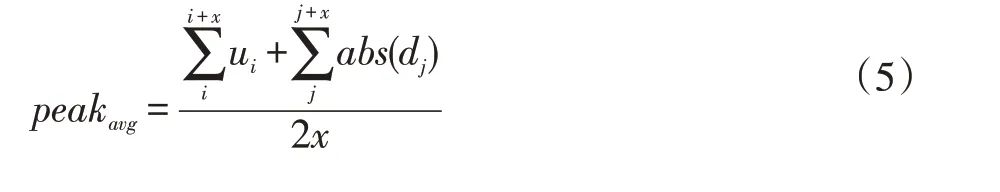
依照公式（5）获取峰值均值，其中abs（）表示求取绝对值。将peakavg作为区分AB 类和CD 类的依据。

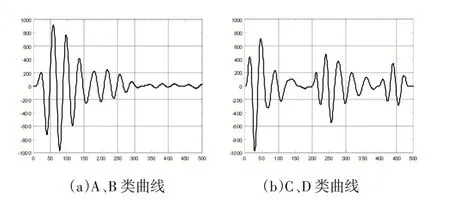
图2 样本数据波形曲线

其次C、D 类的划分根据为其后半段波动起伏情况，与D 类数据相比，C 类数据后段峰值起伏相对较小。计算曲线上下峰值最大值与最小值的比值ratio，并联合peakavg，划分C、D 类数据。

而A、B 类的具体划分依照其曲线波形规则程度。A、B 类曲线前部分起伏较大，而后面部分波形平整，如图3 所示，皆为包括最高峰开始的前4 个峰这段曲线波动起伏明显，而其后的曲线波动较小，基本趋于直线状态。因此对于A、B 类的划分就可以分别从曲线后半段波动起伏程度以及曲线前半段波形下降状态着手。

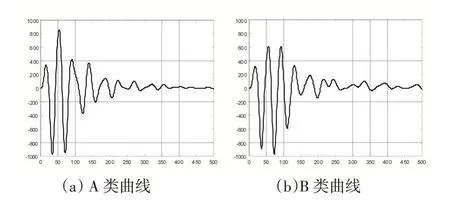
图3 A、B类曲线

以上峰值为例，将曲线最高峰后的第z 个上峰后的部分视为后半段，曲线后半段的波动起伏程度可根据后半段的前p 个峰值均值来进行确定。接着对于曲线前半段，计算上峰值最高峰开始的第1 个峰值与第2个峰值连线k12 的斜率绝对值以及第1 个峰值与第4个峰值连线k14 的斜率绝对值，将这两个斜率值作为判定依据，如图4 所示。

2 具体实验结论与分析

通过对实际工程运用中的锚杆进行测量，获取了本文实验所需的反射信号。共对351 根锚杆进行测量，每根锚杆测量六次，作为一组原始数据保存。然后使用人工分类方法，按照规程[5]对每组锚杆进行等级判断。

图4 斜率绝对值计算示意图

再完成人工筛选后，对原始数据按照第二章所述方法进行预处理得到中间数据。先进行分组分类。实验中，i 取值为5，x 取值为6。根据公式（5），计算峰值均值peakavg，若此峰值均值大于或等于阈值130，则说明该曲线波动较大，判定该曲线属于C、D 类，否则，该曲线属于A、B 类。

其次对于C、D 类的具体划分，除了计算峰值均值，同时还计算上下峰值最大值与最小值的比值ratio，并联合峰值、峰值均值以及比值作为分类依据。若峰值均值peakavg大于或等于阈值200，则判定该曲线属于D类；反之，若峰值均值peakavg在阈值130-200 范围内，同时满足上峰值最大值大于130 且下峰值最大值大于150，且其比值大于或等于阈值10，则判定该曲线属于C 类。

最后对于A、B 类的具体划分，在针对曲线后半段波动起伏程度以及曲线前半段波形下降情况的定量描述中，除了之前已获取的峰值均值，还需计算从最高峰开始的上下峰值的第1 个峰值与第2 个峰值连线的斜率绝对值abs（k12）以及第1 个峰值与第4 个峰值连线的斜率绝对值abs（k14）。

根据峰值、峰值均值以及斜率绝对值的统计结果，可知当曲线除包括最高峰开始的前4 个峰值以外的后6 个峰值均值在阈值范围60 以内，且满足严格连续下降趋势，即曲线前4 个峰值连续递减；或呈总体下降趋势，即曲线上下峰值的第1 个峰值与第2 个峰值连线斜率的绝对值大于第1 个峰值与第4 个峰值连线的斜率绝对值，且除最高峰外的前3 个峰值之间的差值绝对值小于阈值50，满足上述条件的曲线即为A 类曲线。

当曲线从第5 个峰值开始的后6 个峰值均值在阈值范围60-130 以内，曲线前4 个峰值并不满足严格下降趋势，而是满足曲线上下峰值的第1 个峰值与第2个峰值连线的斜率绝对值大于第1 个峰值与第4 个峰值连线的斜率绝对值，但是从曲线第2 个峰值开始，直到曲线的第5 个峰值结束，这个范围内的曲线峰值两两之间差值的绝对值大于或等于阈值50，这样的曲线即为B 类曲线。

3 结语

本文所述锚杆锚固质量等级快速评级方法，通过对原始锚杆数据进行归一化以及进行x 方向修正等预处理操作，得到可供分类的中间数据，然后计算其峰值均值以及相应的斜率绝对值等定量分类标准，从而实现对锚杆锚固质量等级的快速评级。

与目前主流的锚杆锚固质量等级评级方法相比，本文所述方法的优势有以下几个方面：

（1）简单易懂，本文所述方法基于统计结果得到可用来进行分类的阈值，基于阈值进行锚杆锚固质量等级快速评级；

（2）计算量小，仅针对锚杆的杆底反射的时域信号进行处理，能快速得到分类结果；

（3）准确高效，应用该方法得到的分类结果与原人工首次分类的结果存在不一致时，由于人工判定结果具有随意性，人工再次确认基本都能认可本算法分类所得到的结果，表明本算法具有较好的准确性。