受特定变化趋势限制的传感器数据处理方法研究
周俊华,雷孟飞,梁晓东
(湖南联智科技股份有限公司,湖南 长沙 410000)
0 引 言
在物联网传感技术领域,经常需要用到各种各样的传感器对物理世界进行感知,传感器的一般原理是将现实世界的物理量通过各种手段变为电学量,通过标定物理量和电学量之间的对应关系后,则可以通过测量电学量的值反推出被测物理量。
现实世界中的很多物理量在一定的条件限制下,具有限定的变化趋势,如随着时间的变化,松软地面的沉降呈现出递增趋势,混合液体中易挥发组分的含量会呈现递减趋势。对于这些具有明确呈递增或递减变化趋势的物理量,其真实值只有可能在变化趋势内单向变化,而因传感器的原理及其精度等因素的制约,会出现部分测量的原始数据不符合已知的变化趋势的问题,这种明显的错误在数据展示的时候是不能出现的。
常用的处理方法为通过多个同类型的传感器一起测量,然后采用数据融合的算法得到融合结果[1],但是目前针对不同信息的融合算法仍然缺乏合适的评价体系[2];另外基于成本考虑,单传感器的系统目前仍然在大量采用[3];广大学者对单传感器的数据处理方法也进行了很多研究,一般的处理技术可分为基于统计、基于最近邻、基于聚类等方法[4];另外也可基于传感器的系统误差原理,通过滤波的方式进行处理[5],比如曾金芳提出了基于最大熵方法的数据处理[3],宋强提出了极大似然法的数据处理等[6]。
笔者认为对于该类原始数据,其处理具有一定的特殊性。由于事物的“真值”是不可得的,只能通过不断地提高测量精度逼近,所以对于传感器所测量的每一个原始数据,都不能随意地篡改或者剔除,更不能简单地采用拟合或者其他的算法对整个原始数据做替换处理。本文基于可信传感器测量得到的每一个数据,以及使曲线符合限定的变化趋势的原则提出一种数据处理方法,该方法能够通过剔除最少的数据个数来满足上述需求。
1 传感器数据处理算法
1.1 选定数据处理窗口,根据限定趋势找出问题数据点
在原始数据中选取n(n≥3)个连续的原始数据作为一个处理窗口进行数据处理,窗口随时间依次往后推移,最终实现对所有数据的处理。
假设处理窗口内原始数据满足函数关系式Y=F(xi),其中i=1, 2,...,n,n为处理窗口内原始数据的总数量。找出处理窗口内不符合已知限定变化趋势的个别原始数据记为问题数据点,且问题数据对应的序号为jk,其中k=1, 2,...,m,m为问题数据的总数量;如果有连续p个数据不符合变化趋势的则只记录为一个问题数据点,同时引入参数tk,tk=p-1。
1.2 统计所有剔除问题数据事件的取值
对于序号为jk的问题数据点分别判断其前后相邻的原始数据是否符合处理窗口内原始数据的变化趋势,若在序号为jk的问题数据之前相邻的原始数据有不符合的,记为事件Jk1并统计事件包含的问题数据个数,若在序号为jk的问题数据之后相邻的原始数据有不符合的,记为事件并统计事件包含的问题数据个数。
变化趋势受限定则说明数据满足呈递增变化趋势或递减变化趋势,递增量(即后一个大数减去前一个小数的值)或递减量(即前一个大数减去后一个小数的值)大于等于0。
(1)若处理窗口内的原始数据的变化趋势为递增变化趋势,则:
如果F(xj)≥F(xj-2),则处理窗口内序号jk之前的原始数据已经符合递增变化趋势,事件Jk1包含的问题数据个数为剔除的数据数量加上tk。
如果F(xj)<F(xj-2),取jk=jk-1,若jk-1>jk-2,则返回步骤①;若jk-1≤jk-2,则结束,删除小于等于jk且大于jk-1之间的所有数据。
如果F(xj+1)≥F(xj-1),则处理窗口内序号jk之后且序号jk+1之前的原始数据已经符合递增变化趋势,事件包含的问题数据个数为剔除的数据数量。
如果F(xj+1)<F(xj-1),取jk=jk+1,若jk+1<jk+1,则返回步骤①;若jk+1≥jk+1,则结束,删除大于等于jk且小于jk+1之间的所有数据。
(2)若处理窗口内的原始数据的变化趋势为递减变化趋势,则:
①对于Jk1事件,具体是:剔除序号为jk-1的问题数据;判断序号为jk-2的原始数据Y=F(xj-2)与序号为jk原始数据Y=F(xj)的关系。
如果F(xj)≤F(xj-2),则处理窗口内序号jk之前的原始数据已经符合递减变化趋势,事件包含的问题数据个数为剔除的数据数量加上tk;
如果F(xj)>F(xj-2),取jk=jk-1,若jk-1>jk-1,则返回步骤①;若jk-1≤jk-1,则结束,删除小于等于jk且大于jk-1之间的所有数据。
如果F(xj+1)≤F(xj-1),则处理窗口内序号jk之后且序号jk+1之前的原始数据已经符合递减变化趋势,事件包含的问题数据个数为剔除的数据数量;
如果F(xj+1)>F(xj-1),取jk=jk+1,若jk+1<jk+1,则返回步骤①;若jk+1≥jk+1,则结束,删除大于等于jk且小于jk+1之间的所有数据。
1.3 选取最优剔除事件的集合
若上述不存在多组A值相等的情况,则所得数据为最终保留数据;若上述存在至少两组A值相等的情况,则分别记为Ap,p为1, 2,...,q,q为A值相等的总组数。对多组A值相等的数据采用线性方程最小二乘法进行数据拟合,结合偏差平方和来进行辅助判断,如下:
对原始数据函数Y=F(xi)进行拟合,得到拟合函数Yi=f(xi)=a'xi+b',其中i=1, 2,...,n,求出a'和b'的值。

比较σ2p值之间的大小,选取数值最小的偏差平方和作为最优解,所述最优解对应的数据剔除方案为最优方案,采用最优方案剔除数据后得到最终保留数据为最佳处理结果。
2 实例验证
采用激光测距仪测量一处具有沉降趋势的淤泥堆积场的表面高度变化情况,由于淤泥具有沉降趋势,所以测量数据应该呈现限定的递增变化趋势。原始数据见表1所列。

表1 原始数据表
在原始数据中选取n=24(n≥3)个连续的原始数据作为一个处理窗口进行处理,窗口内不符合原始数据变化趋势的数据点为j1=7,j2=15和j3=20,且t1=0,t2=0,t3=1。
(1)对于J11事件,剔除序号为j1-1=7-1=6的问题数据之后,判断序号为j1-2=7-2=5的原始数据Y=F(xj-2)=F(x5)与序号为j1=7的原始数据Y=F(xj)=F(x7)的关系。
因F(x7)≥F(x5),所以处理窗口内序号j1=7之前的原始数据已经符合递增变化趋势,事件包含的问题数据个数为1。
(2)对于J12事件,剔除序号为j1=7的问题数据之后,判断序号为j1+1=7+1=8的原始数据Y=F(xj+1)=F(x8)与序号为j1-1=7-1=6的原始数据Y=F(xj-1)=F(x6)的关系。
因F(x8)<F(x6),所以继续剔除序号为j1+1=7+1=8的问题数据,判断序号为j1+2=7+2=9的原始数据Y=F(xj+2)=F(x9)与序号为j1-1=7-1=6的原始数据Y=F(xj-1)=F(x6)的关系。
因F(x9)≥F(x6),则处理窗口内序号j1=7之后且序号j2=15之前的原始数据已经符合递增变化趋势,事件J12包含的问题数据个数为2。
依此类推,分别判断序号为j2和j3的问题数据的情况,求得 :J11=1,J12=2,J21=1,J22=1,J31=3,J32=2。
将上述的事件J11,J12,J21,J22,J31和J32包含的问题数据个数按照表达式A=min(J11,J12)+min(J21,J22)+min(J31,J32)=min(J11,J21,J32)=min(J11,J22,J32)=1+1+2=4计算出最少问题数据个数A,得到相应的剔除问题数据最少的方案。由于有两种方案得到的A值相等,所以继续进行后续的处理判断。
对处理窗口内的原始数据采用线性方程最小二乘法进行数据拟合,得到拟合函数Yi=f(xi)=a'xi+b',其中i=1, 2,..., 24;求出a'=0.133 7和b'=5.378 3。
上述两组A值相等的情况分别记为。

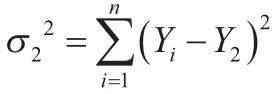
比较σ12和σ22值的大小,选取数值最小的偏差平方和σ22作为最优解,所述最优解对应的数据剔除方案为最优方案,采用最优方案剔除数据后得到最终保留数据为最佳处理结果,如图1所示。
3 结 语
基于剔除最小数据量的原则进行受特定变化趋势限制的单传感器的数据处理,通过采用平滑窗口的方法依次处理所有数据,采用直观选取不符合变化趋势的数据并通过穷举法结合排列组合选出剔除数据量最小的方案,对于存在多种情况得到剔除同样数据量的方法,则继续利用线性方程最小二乘法拟合并分别求取偏差平方和的方法,比较其离散程度,选取较小的值对应的方案作为最佳处理方法。结果表明,使用该方法能够通过剔除较少的误差数据使受特定变化趋势限制的传感器数据符合变化趋势,并且曲线整体变化平稳,可信度较高。本文方法能有效地解决现有技术中存在的因传感器测量得到的部分数据不符合已知变化趋势的问题。

