临近空间高超声速空腔几何特性的DSMC研究
张隽研,王学德
(南京理工大学 能源与动力工程学院,江苏 南京 210094)
临近空间高超声速飞行器的气动布局与外形设计一直是近年来研究的热点问题。由于临近空间大气的特殊性,在该空域飞行的飞行器,其结构强度及热力学防护主要受到气动力和气动热的影响,因此,其外形布局的设计尤为重要。在实际应用中,在飞行器的表面往往需要增加一定的空腔结构来满足和强化具体的应用需求,如在高超声速飞行器钝头体的前缘点引入空腔结构,可以使飞行器头部空腔的外缘形成“冷却环”,有效降低了局部热流[1];高超声速火箭撬试验中,为了方便试验体的安装与固定,火箭撬下方的滑轨会与试验体之间形成空腔结构[2];用于增强高超声速飞行器机动性的空气舵,其底部也设计为便于安装的类似空腔结构的缝隙[3];制造公差、非相似材料的不均匀碰撞或者传感器的安装,导致飞行器的表面不可避免地出现缝隙或缺陷这种类空腔结构,使飞行器在飞行过程中出现安全隐患[4]。以上应用都基于空腔这一基本的几何外形。为了更好地解决带空腔高超声速飞行器空腔几何结构的设计,需要对临近空间空腔几何特性及腔内流动问题进行研究。
空腔流动问题一直是空气动力学研究的经典问题之一,高速自由流流过空腔时,会形成2种基本的流动结构,即空腔内的剪切层及低速的再循环区域[5-6]。根据剪切层对空腔内部再循环区域的影响,空腔分为闭式和开式两大类[7]。开式空腔和闭式空腔内流体的流动特性并不相同。对于开式空腔,剪切层和边界层并未触及腔体底部,高速自由流对剪切层的冲击使其产生自持振荡,这使得空腔周围的气动噪声增大,给腔内的部署设施以及空腔自身结构的安全带来隐患;对于闭式空腔,边界层和剪切层逐渐触及腔体底部,空腔内再循环区域一分为二,使得空腔底部的压强增大,对空腔内部组件的安全分离产生不利的影响[8]。
国内外许多学者对连续流区域的空腔进行了很多数值模拟和实验研究工作,但是对于稀薄流区域的空腔研究较少。靳旭红等[9]研究了70 km,75 km,80 km,90 km 4个不同高度下稀薄流域高超声速缝隙流动问题,并分析了稀薄气体效应对缝隙内部流动结构和壁面热流的影响。Palharini等[4,10]首先对比了高超声速稀薄流动条件下,二维空腔与三维空腔内部的传热系数、压力系数与摩阻系数,结果表明腔体后缘y方向上二维算例的传热系数比三维算例的值大几倍,而腔体底部x方向的值吻合良好。随后其又研究了70 km高度处、马赫数为25时不同长深比对空腔壁面空气动力学特性的影响,发现长深比为4时空腔内部流动结构发生改变。Guo[11]采用结构网格,研究了60 km高度处、马赫数为8时不同长深比以及不同高度的前、后壁面对空腔内再循环区域以及剪切层的影响。
至今,学者们对稀薄流区域的不同高度以及不同马赫数下空腔由开式变为闭式的具体长深比数值还没有给出定量的研究计算,对稀薄流区域的空腔的研究,给出的高度跨度以及马赫数跨度还不够广。因此,本文从稀薄流临近空间出发,以空腔作为研究对象,研究高度为50~90 km,马赫数为5~20。由于直角坐标网格在处理倾斜壁面时需要对单元格进行切割处理,对物面的处理相对复杂,基于此,本文利用非结构网格良好的贴体性以及生成的便利性,研究了不同倾斜角下的空腔前壁面对空腔内再循环区域的影响。
1 计算方法
1.1 DSMC方法介绍
DSMC 方法是直接研究分子的微观运动的统计学方法,克服了解玻尔兹曼方程的复杂性。该方法通过大量的模拟分子来仿真真实分子的微观运动情况。其本质是在时间步长Δt内,通过运动子程序和碰撞子程序将分子的运动和分子的碰撞这2个耦合的过程进行解耦,通过采样子程序采集到每个流场单元的宏观流动数据,最后按单元编号将数据输出。DSMC方法中,网格起到以下2个作用[12]:一是空间离散化宏观流场;二是有利于选取分子碰撞对。
本文计算网格采用非结构贴体网格,分子模型采用变径硬球(VHS),能量交换模型采用Larsen-Borgnakke模型,物面采用恒温壁面边界条件,反射模型采用Cercignani-Lampis-Lord(CLL)完全漫反射模型。
1.2 算例验证
本文采用圆柱绕流模拟算例来验证程序的有效性,圆柱绕流的示意图如图1所示,其中Kn为克努森数,用于表征空气的稀薄程度。计算条件取自文献[13],模拟气体为氩气,模拟分子个数为151万,计算网格数为61 336,程序循环步数为20 000。来流速度v、来流温度T、来流密度ρ、物面温度Tsurf、马赫数以及时间步长Δt的设置见表1。
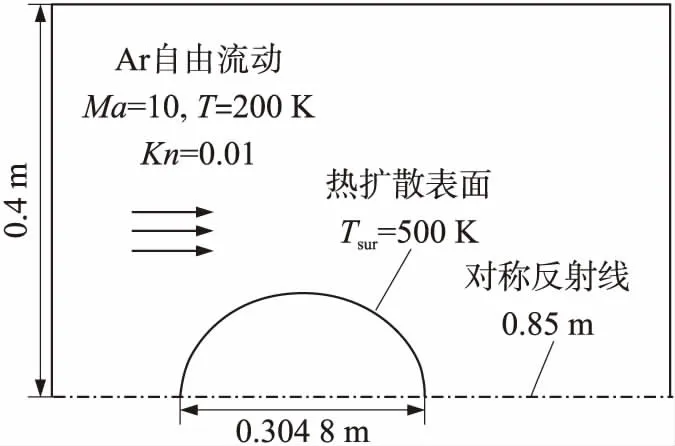
图1 圆柱绕流示意图
表1 计算参数
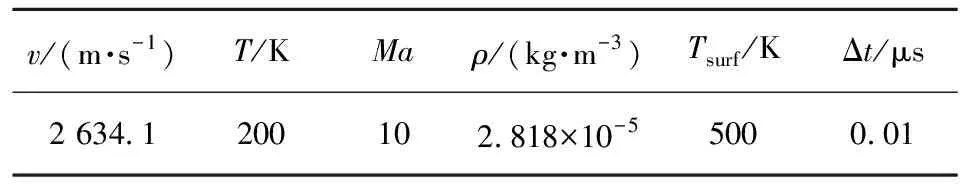
v/(m·s-1)T/KMaρ/(kg·m-3)Tsurf/KΔt/μs2 634.1200102.818×10-55000.01
图2给出了按表1参数条件运行的密度、温度和压力的等值线图。图3给出了本文圆柱绕流的压力系数Cp、摩阻系数Cf和表面传热系数Ch计算结果与文献[13]的比较,图中的横坐标Φ为圆柱表面的切线与x轴正方向所成的角度。由图可以看出,本文的计算结果与文献值吻合较好,验证了本文程序采用非结构网格计算的正确性。
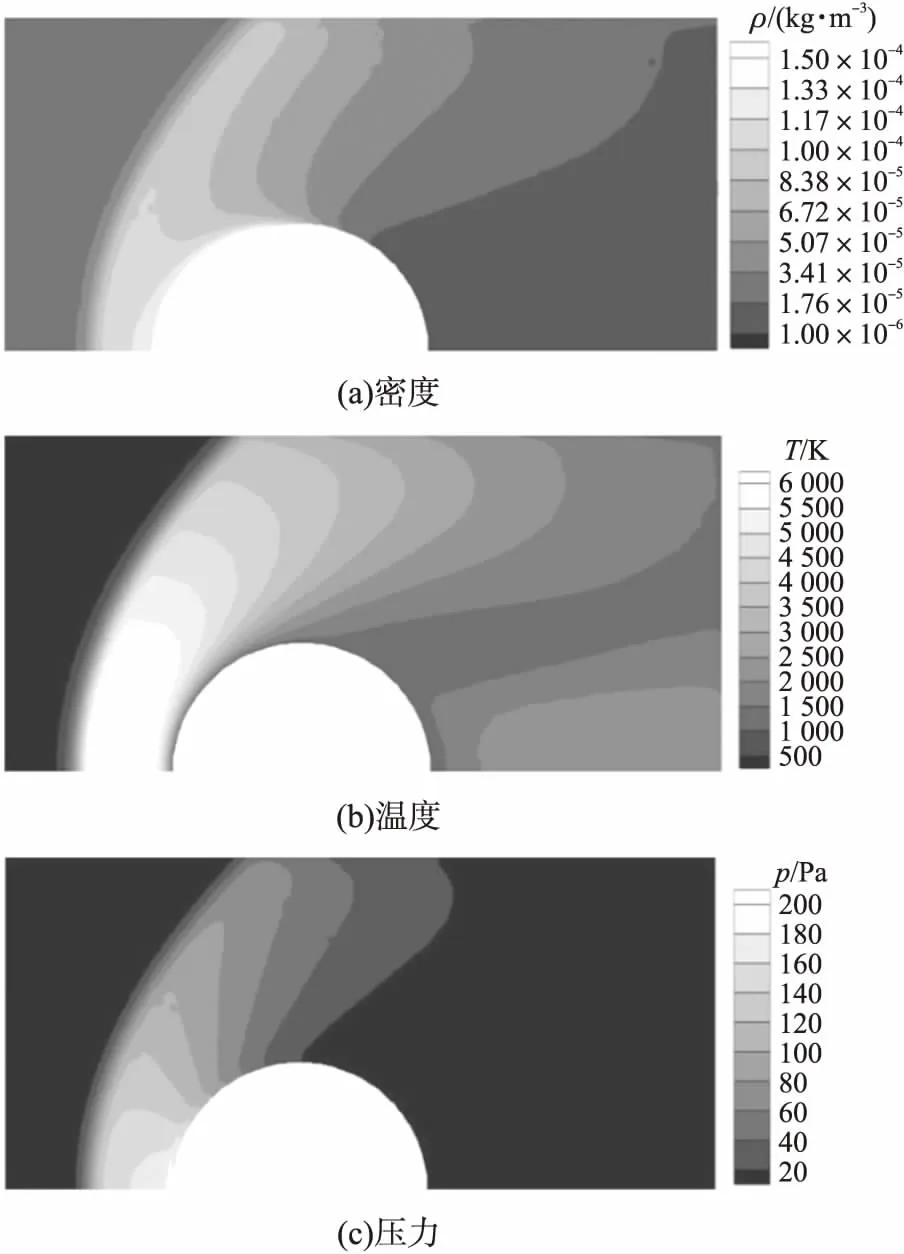
图2 圆柱绕流的密度、温度、压力等值线图
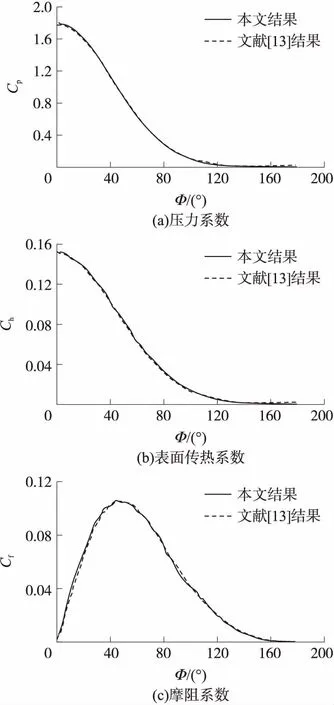
图3 圆柱绕流计算结果与文献[13]结果的比较
2 空腔的几何特性研究与分析
2.1 模拟参数的设置
定义空腔底部长度L与深度D的比值为长深比。本文取L/D=1~10,长深比间隔为1,以及前壁面倾斜角θ=30°,45°,60°,75°,研究空腔内再循环区域的流动特征,模拟高度H=50 km,60 km,70 km,80 km,90 km,来流速度Ma=5,10,15,20。不同高度下的来流条件见表2,表中,n为分子的数密度。由于高度的不同,空气的稀薄程度也不尽相同,网格尺度约为分子自由程的1/3,时间步长与来流速度的乘积要小于网格尺度,每个网格中的模拟分子数约为20~30。表3给出了L/D=6时不同高度算例中网格数K、分子数N与时间步长Δt的具体设置。本文研究计算的空腔模型如图4所示。
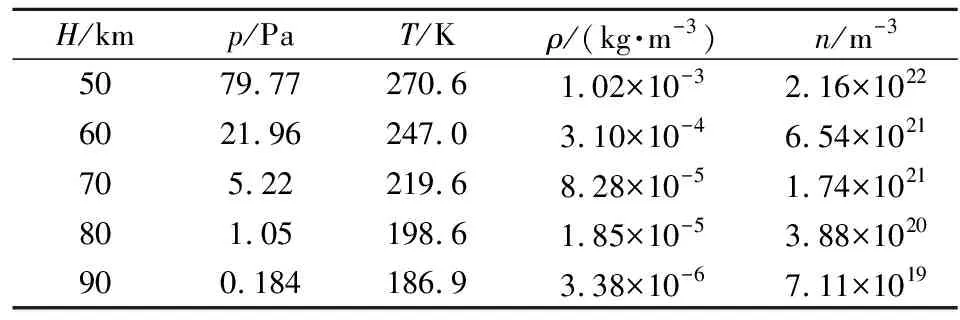
表2 不同高度高超声速来流条件
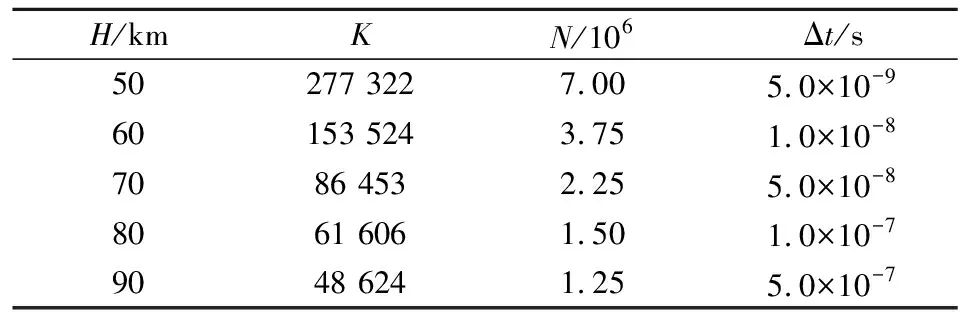
表3 不同高度,L/D=6算例的计算参数
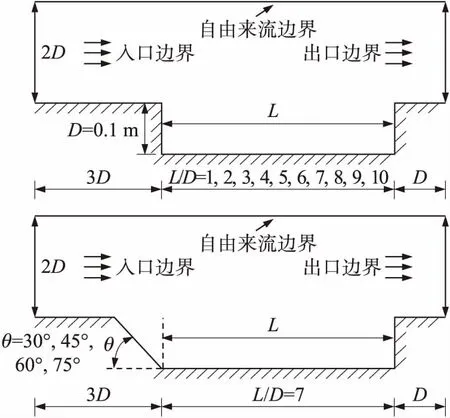
图4 空腔几何形状示意图
2.2 网格无关性验证
DSMC方法的计算精度主要取决于网格密度、采样次数、每个网格单元中的粒子和时间步长。根据经验,采样时间、每个网格单元中的粒子数量和时间步长都设置为适当的值,仅研究网格尺度的影响。时间步长Δt、网格数K以及分子数N的设置见表4。

表4 网格验证计算参数
定义一个无量纲参数Ω来研究网格尺度对计算结果的影响,其表达式为
(1)
式中:a为修正系数,这里取值为1.009;s为网格单元的平均线性尺寸,即相邻节点之间的平均距离;λ为来流分子的平均自由程;Kn为来流的克努森数;l为流场的特征长度。以50 km处L/D=6,Ma=10,取空腔前沿X=-0.3 m至X=0 m处物面的体积热流密度Q的算例为例,计算3套Ω值分别为1,0.67和0.33的网格,来验证3种尺度网格的独立性,计算结果如图5所示。3种不同尺度网格的局部放大图如图6所示。可以看出,每个网格尺度的热流密度很好地相互吻合,Ω=0.33和Ω=0.67尺度的网格计算结果几乎重合。为了减小计算损耗,选择中等网格作为计算网格处理下文中的各种工况。
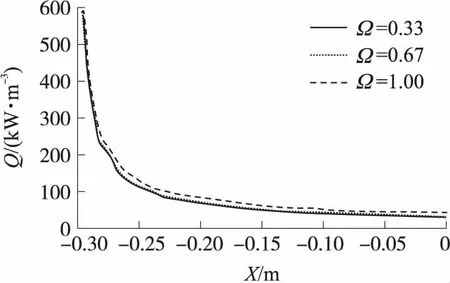
图5 3种不同网格尺度的热流密度对比
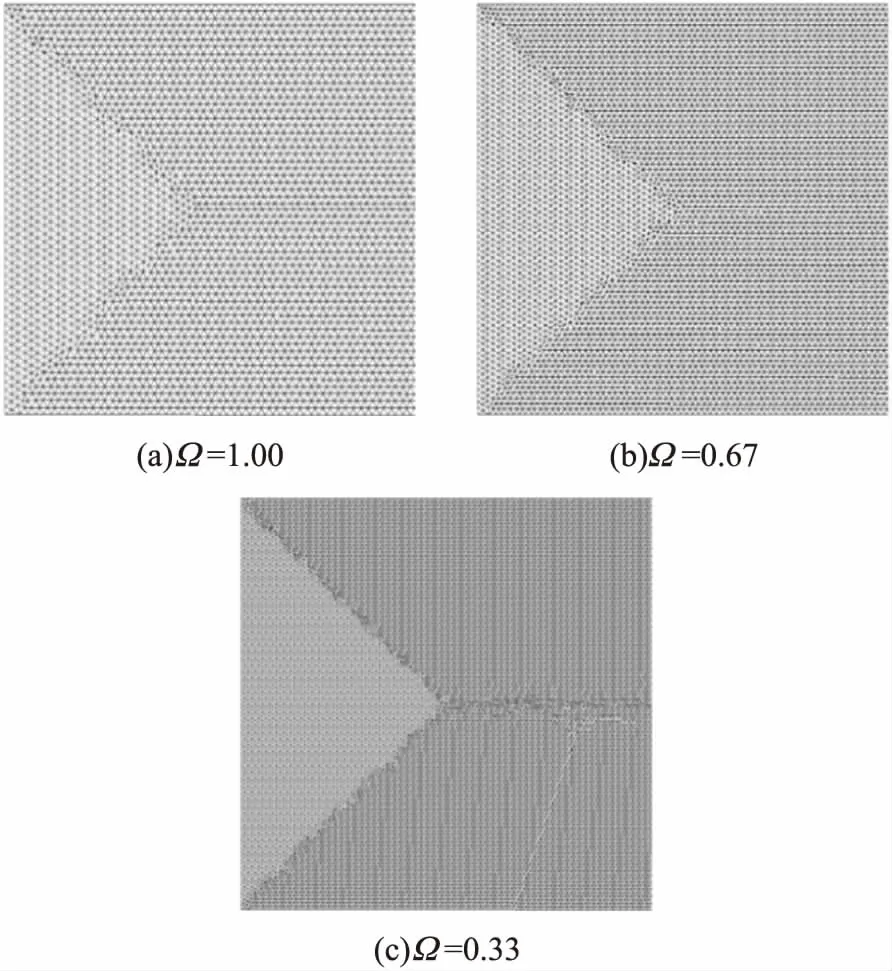
图6 3种不同尺度网格的局部放大示意图
2.3 不同长深比(L/D)对空腔流场的影响
首先以60 km的高度为例,空腔的长深比为1~10,间隔为1。图7给出了高度为60 km时不同长深比下马赫数的等值线图,图中以流线的形式标识了空腔中的再循环区域以及剪切层中的流动。可以看到,当长深比从1逐渐增加到10时,边界层也经历着显著的变化,剪切层区域为图中的浅灰色区域,该区域通过流线标识,如图7的图例所示。

图7 60 km处不同长深比的马赫数等值线及再循环区域示意图
当长深比小于4时,空腔内的再循环区域仅有一个,随着边界层的挤压效应,空腔内的再循环区域逐渐地一分为二。空腔内当L/D≥6时,剪切层逐渐触及到空腔底板,使再循环区域分为2个独立的循环区域,此时称空腔由开式变为闭式。
文献[14]中提出,长深比通常用于对空腔进行分类,以长深比L/D=10为空腔变形极限值,当L/D>10时空腔由开式变为闭式。根据本文的计算结果,在临近空间高度为60 km处,当L/D>6时,空腔呈闭式。也就是说,文献[14]中提到的用于分类空腔类型的标准不再适用于稀薄高超声速流动的情况。文献[15]中,空腔深度保持在3 mm,长深比分别为1,2,3,4,5,模拟所用的自由流动条件为:来流速度7 600 m/s,高度80 km,在这种情况下,即使L/D=3,空腔依然会变形,而L/D=4,5时,空腔变为闭式。因此,一个重要的发现是,用于区分空腔类型的标准(即L/D)不是恒定的,而是随自由流条件而变化。将本文的计算结果与文献[15]的结果比较后可以得出,对于具有更高海拔和更大速度的自由流动,L/D的标准会变得更低。本节旨在找出不同高度及不同马赫数时使空腔由开式变为闭式的具体长深比(L/D)的值。
本文还计算了其他高度及马赫数时空腔由开式变为闭式时的临界值,具体结果见表5。由于50 km和60 km处Ma=5的工况下空腔发生类型转变的长深比值均大于10,超出了本文的计算范围,因此表5中并未给出具体数值。60~90 km处Ma=10,15,20的闭式空腔流动示意图如图8所示。
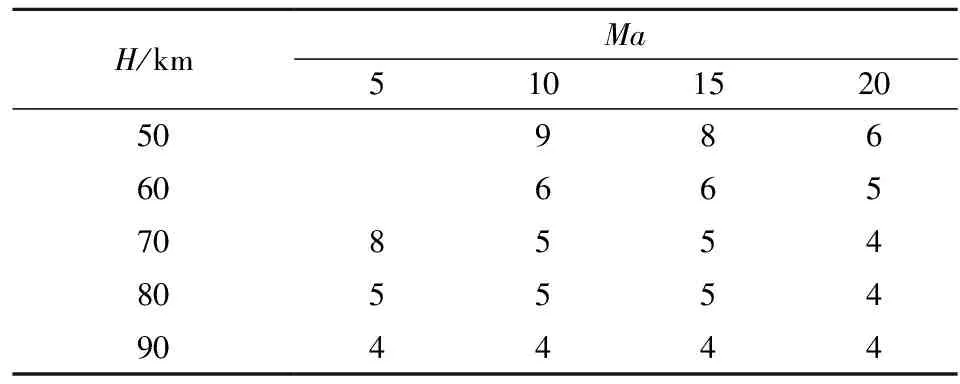
表5 空腔由开式变闭式的L/D临界值
从表5中可以看出,随着高度的增加空腔由开式变为闭式的长深比的值在逐渐减小,并且随着马赫数的增加,空腔发生变形的长深比值也呈减小趋势,并且高度对空腔发生形变的影响大于马赫数的影响。当Ma=5时,不同高度下空腔发生变形的长深比临界值的间隔很大,该间隔随高度的增加而减小,并且,该间隔随马赫数的增加也呈减小趋势。H=50 km时,马赫数对空腔发生变形的长深比的数值的间隔影响也较大,长深比L/D的数值间隔随着马赫数的增加而减小,并且,随着高度的增加,长深比的间隔也呈减小趋势。H=90 km时长深比不再随马赫数的变化而变化,当Ma=20,H>70 km时,L/D的值也不再因高度的变化而发生改变,因此,邻近空间区域内空腔由开式变闭式的长深比临界值的极限为4。

图8 不同工况下空腔由开式变闭式的流线图
将空腔内部壁面的长度进行归一化处理,定义前壁面为S1,其无量纲量长度为L1;底部壁面为S2,其无量纲长度为L2;后壁面为S3,其无量纲长度为L3,如图9所示。60 km处Ma=10的空腔后壁面处表面传热系数随长深比的变化趋势分别如图10和图11所示,从图中可以看出,随着长深比的增大,空腔壁面的表面传热系数也呈增大趋势,并且该趋势与文献[4]中的结果吻合。随着无量纲长度的增加,长深比大于7时表面传热系数呈先增大后减小趋势,原因在于长深比过大时会在空腔后方产生再附激波,对流场产生一定影响,并且分子撞击后壁面会反射使得近壁面处速度降低,也会使热流密度下降。

图9 空腔壁面无量纲长度示意图
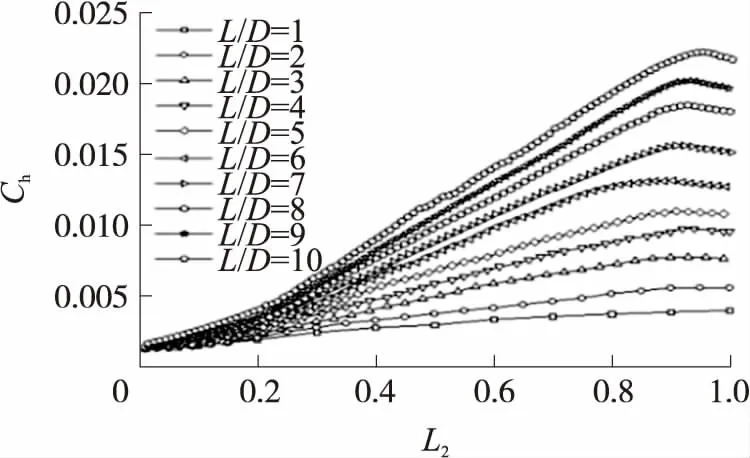
图10 空腔底部面壁S2的表面传热系数
2.4 不同物面倾角对空腔内流场的影响
以60 km处,Ma=10,L/D=7的工况为例,通过观察空腔内的再循环区域,研究物面倾角对其流动特性产生的影响。
不同倾斜角下马赫数的等值线图如图12所示,物面倾角分别设置为θ=30°,45°,60°,75°。从图中可以看出,剪切层对左侧空腔底部的挤压效应随左侧物面倾斜角的增大而减小。倾角θ=30°时,边界层几乎完全触及空腔左侧底部,使左侧的再循环区域完全消失,而右侧再循环区域几乎不受影响。当θ>60°时,左侧出现较小的再循环区域。随着倾角的增大,左侧再循环区域也逐渐扩大,因此在保证空腔的空气动力学性能的前提下,减小壁面倾角可以有效地减少再循环区域对空腔的影响。以本文研究内容为例,空腔壁面倾角为30°为宜。将前、后壁面的倾角同时设置为30°,马赫数等值线图如图13所示,由图可见,空腔内流动稳定,没有出现再循环区域。

图12 不同壁面倾角下的马赫数等值线图
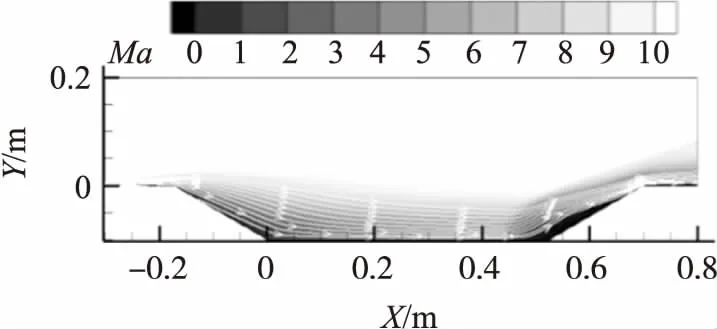
图13 前、后壁面倾角均为30°时的马赫数等值线图
空腔前壁面不同倾角的表面传热系数如图14所示。
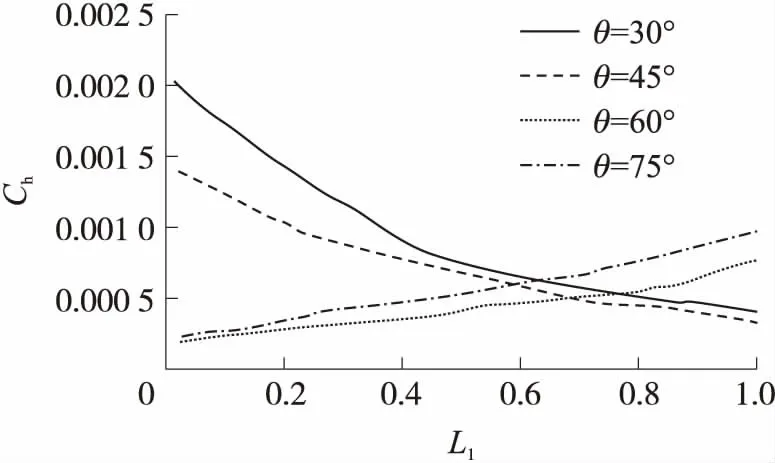
图14 不同壁面倾角时壁面S1的表面传热系数
当θ≥60°时,该壁面处表面传热系数的大小由空腔左侧的再循环区域决定,因此θ=75°算例的表面传热系数大于θ=60°算例;当θ≤45°时,该壁面处表面传热系数的大小由自由来流决定。与θ=45°的算例相比,θ=30°算例的空腔前壁面受到自由来流的影响更大,因此该算例下空腔前壁面的表面传热系数更大。
3 结论
本文研究了不同高度以及不同马赫数下不同的长深比L/D对空腔内在循坏区域的影响,以及在固定的长深比下,不同的物面倾角θ对空腔内在循环区域的影响。主要得出以下结论:
①找出了不同高度和马赫数下空腔内流动结构发生形变的L/D的临界值,发现高度和速度的增加可以使该临界值变小,且L/D=4为该临界值的极限值。
②减小物面的倾角可以使剪切层更易触及空腔底部,有效地消除空腔内的再循环区域,30°以下的角度为消除再循环区域且防止再次生成再循环区域的适合角度。
③空腔底部壁面与后壁面的表面传热系数随长深比L/D的增大而增大。当壁面倾角θ≥60°时,空腔前壁面的表面传热系数随θ的增大而增大;当壁面倾角θ≤45°时,空腔前壁面的表面传热系数随θ的增大而减小。

