高旋二维弹道修正弹的角运动特性
朱 煌,史金光,谢 飞,徐东辉
(1.南京理工大学 能源与动力工程学院,江苏 南京210094;2.辽沈工业集团有限公司 研发中心设计二所,辽宁 沈阳110045)
弹道修正弹成本低、命中精度高、附带毁伤小,在现代战争中具有至关重要的地位。精确制导组件(precision guidance kit,PGK)是美国陆军最早提出的高旋二维弹道修正弹引信项目,通过在常规炮弹上加装低成本GPS制导引信组件实现炮弹精度的提高[1]。近年来,美国ATK公司研究的PGK为典型代表,通过控制固定鸭舵相对于弹体的滚转角度,使操纵舵在大地坐标系中的位置固定,由此产生相应的修正力与力矩来实现弹道精确控制[2]。美国军方提出的XM1156“精确制导组件(PGK)”二维弹道修正引信,预期的圆概率误差达到50 m[3]。文献[4-5]建立了该类弹丸角运动方程,研究了其飞行稳定性及其在脉冲力作用下的运动特性。文献[6-7]研究了弹丸在重力和控制力作用下的动态响应特性、强迫运动特性等问题。张嘉易等[8]研究了鸭舵修正机构的气动特性,对几种不同形状、不同面积鸭舵的阻力、升力及各项力矩进行了分析,并研究了不同形状舵片在相同时间点进行弹道修正后的修正能力。袁备等[9]对不同舵偏角和受力面积下的鸭舵所受阻力、升力和导转力矩以及相关系数进行动力学仿真。许诺等[10]基于周期平均的概念提出一种能连续地控制平均法向力的大小和方向的修正方法。吴映锋等[11]研究了无控、有控时弹丸的攻角与速度运动特性。
本文在上述研究成果的基础上,建立了高旋二维弹道修正弹的角运动方程,推导了弹丸在起始扰动作用下的攻角与速度偏角的变化关系,研究了弹丸在脉冲控制力和固定方位控制力长时间作用的2种情况下的弹轴运动特性,进行了数值计算分析,验证了在控制力作用下的攻角、速度偏角规律,为控制策略与控制方案的设计提供了理论依据。
1 PGK组件概述
PGK组件由互相垂直的2对舵面组成,1对旋转舵片按照相同舵偏角差动安装,来流在2个舵面产生大小相等、方向相反的气动力,其合力为0,如图2所示。产生的合力矩使弹轴旋转,同时在舵面上生成相应的滚转阻尼力矩反对弹丸滚转,滚转阻尼力矩随着转速增大而增大,当2个力矩的和为0时,转速达到平衡。

图1 鸭式布局双旋弹结构示意图
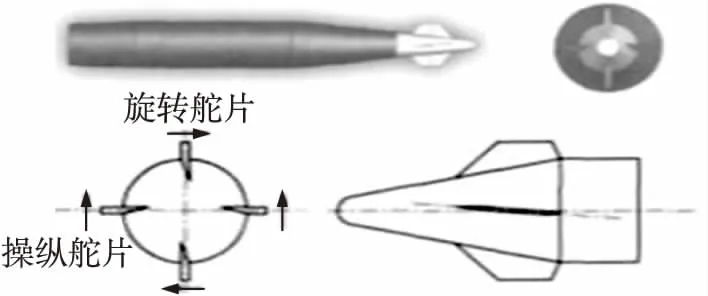
图2 PGK组件舵面安装情况
1对操纵舵片按同向偏转固定角安装,2片舵面上产生的升力方向相同,升力对弹丸质心形成的力矩影响弹丸角运动,产生攻角,影响全弹的气动力,进而改变弹丸的运动轨迹。
2 高旋二维弹道修正弹的角运动模型
对于高旋二维弹道修正弹,由于PGK组件的质量、体积相对于全弹来说较小,故可以忽略其质量和体积,不改变全弹的质量分布特性与轴对称性,主要考虑组件增加的控制力和力矩。通过在无控弹角运动基础上增加控制组件提供的控制力和力矩来建立其角运动方程。
建立的攻角角运动方程为[12]
Δ″+(H-iωp)Δ′-(kz+iωpMT)Δ=G
(1)

速度偏角方程为[12]

(2)
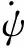
方程(1)右端的G为非齐次项,包含重力的影响、风的影响、轻微不对称因素的强迫作用、控制力和力矩的作用等。
在一段弹道上,认为空气动力变化较小,近似看作常数,攻角方程(1)和偏角方程(2)就可作为常系数微分方程,对其进行求解。
3 高旋二维弹道修正弹的角运动特性
3.1 起始扰动作用下弹丸的角运动特性
Δ″-iωpΔ′-kzΔ=0
(3)
其特征方程的特征根为
(4)
式中:
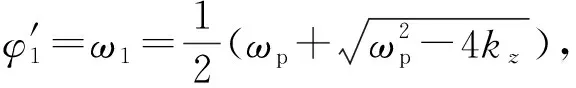
其中:φ′j=ωj,j=1,2,是对飞行弧长而言的角频率。
考虑静力矩为翻转力矩,弹丸满足陀螺稳定性时,方程(3)的解为
Δ=C1eiφ′1s+C2eiφ′2s
(5)
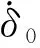
(6)
或
(7)
式中:
ω1t=ω1v0,ω2t=ω2v0
(8)
(9)
式(7)表示弹轴绕速度线的攻角运动是由2个圆运动合成,2个圆的幅值相等,角频率均为正,即2个圆运动方向相同,其合成运动的曲线为外摆线,如图3所示。

图3 起始扰动时的攻角曲线
3.2 起始扰动作用下的平均速度方向
方程(2)描述了速度方向围绕理想质点弹道速度方向的变化规律。当存在攻角Δ=δ1+iδ2时,由攻角产生的升力方向与复攻角矢量方向平行,大小为mbyv2|Δ|,速度方向根据升力的方向偏转,即满足偏角方程(2),则
ψ′=ψ′1+iψ′2=byΔ
(10)
由于ψ′的方向是沿偏角ψ变化的切向,所以从几何上讲,ψ′平行于攻角曲线的割线。
(11)
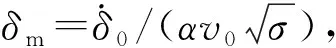
(12)


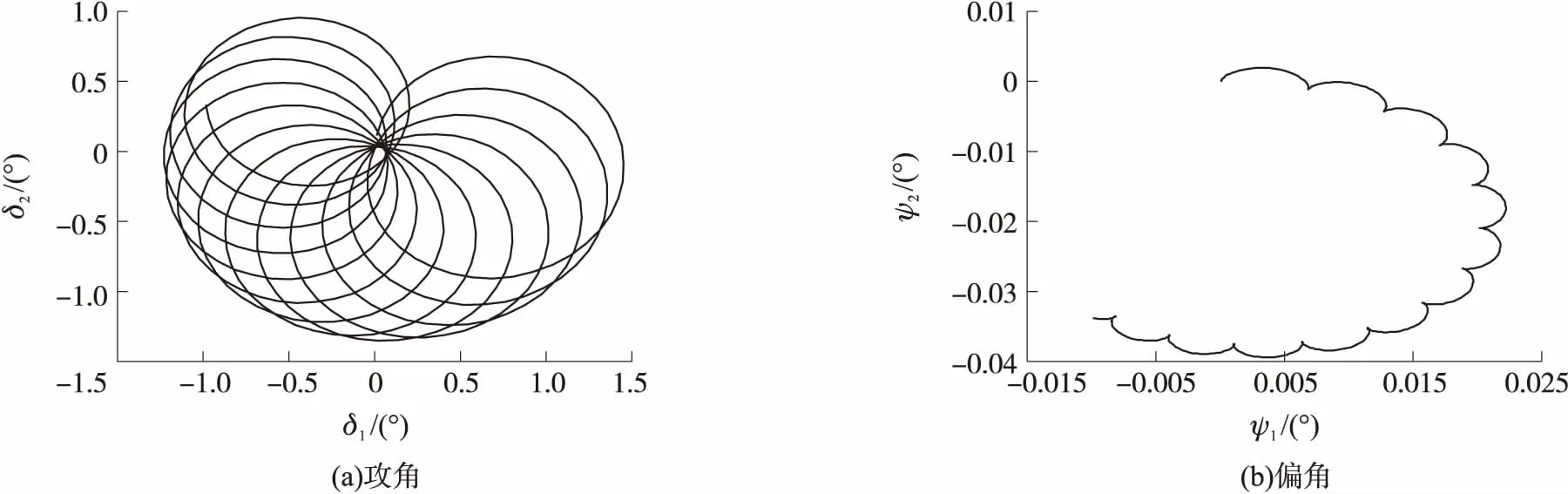
图向上时0.5 s内的攻角曲线、偏角曲线

图向下时0.5 s内的攻角曲线、偏角曲线


图向右时0.5 s内的攻角曲线、偏角曲线

图向左时0.5 s内的攻角曲线、偏角曲线

3.3 控制力瞬时作用下的弹轴运动特性
弹丸受到瞬时控制力是指升力舵面短暂地锁定停留在某一方位一段很短的时间Δt,形成此方向的升力和控制力矩,此后解锁,舵面相对弹体自由旋转而不提供确定方位的升力。此时可看作在普通力作用基础上增加了瞬时控制力矩时的作用效果。
以下假定攻角较小,气流始终与舵面垂直,升力与舵面垂直,大小不变。分析舵面产生向上和向下方向的控制力时,对弹丸质心产生控制力矩作用下的攻角和偏角变化规律。
图8、图9分别为产生向上、向下的控制力时的弹轴运动规律。
对比图8与图4、图9与图5可见,二者的运动规律相似,瞬时控制力所产生的平衡攻角、平均速度偏角的方向与瞬时控制力方向大致相反。
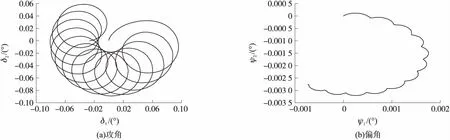
图8 控制力向上,0.5 s内的攻角曲线、偏角曲线

图9 控制力向下,0.5 s内的攻角曲线、偏角曲线
3.4 控制力较长时间作用下的弹轴运动特性
固定方位控制力指在小攻角条件下,舵面长时间停留在某个方位而形成固定方向控制力和控制力矩,从而研究弹丸角运动的长期平均响应。
此时弹丸受到平行于弹轴的气流,由升力面固定舵偏角δD产生升力FD0,FD0就是控制力,方向沿舵面法线方向。
以弹轴坐标系Oξηζ[12]的近似铅直面Oξη为弹体滚转角的零位置,设舵面法线方向相对于此零位置的滚转角为φD,则升力FD0也在φD方向,它沿弹体坐标系Oη和Oζ的分量为FDη和FDζ。设Oη为复数平面的实轴,Oζ为虚轴,故舵面升力的复数形式为
FD=FDη+iFDζ
(13)
设固定舵面压力中心到弹丸质心的距离为lG,则升力对弹丸质心产生的力矩为
MD=MDη+iMDζ=iFDlG
(14)
弹丸绕质心转动方程为
(15)
式中:ωη,ωζ分别为沿实轴和虚轴的转速分量;MDη,MDζ为增加的控制力矩。将式(15)第1式乘以(-i),再与第2式相加,得到摆动角Φ的复数方程,再与偏角方程相减,得到攻角方程:
Δ″+(H-iωp)Δ′-(kz+iωpMT)Δ=
[|FD|lG/(JAv2)]eiφD
(16)
将方程(16)的解代入偏角方程(2)中积分,可得到飞行速度方向的变化规律。
假设在一段弹道上,方程(16)中系数变化较小,近似看作常数处理,即方程(16)为线性常系数方程。
舵面方位角φD随着控制策略不同而变化,假设它在一段弹道上为常数,即固定舵停留在某一方位角φD不变,平行于弹轴的气流产生大小不变的控制力矩|FD|lG,方程右端为常数项,则方程解为
Δ=δ1+iδ2=C1e(λ1+iω1)s+C2e(λ2+iω2)s+ΔD
(17)

-(kz+iωpMT)Δ=[|FD|lG/(JAv2)]eiφD
其稳态解为
(18)
式中:KD=|FD|lG/(JAv2)。
可见,在固定方位φD舵控力作用下,攻角经过一段时间运动后达到平衡值ΔD。
当不考虑马格努斯力矩项时,即MT=0,则式(18)可写成:
(19)
此时平衡攻角ΔD的方位与舵面法线方向φD相反,相差180°。
当考虑马格努斯力矩项时,即MT≠0,式(18)可写成:
(20)
式中:Δφ=-arctan(ωpMT/kz),由于马格努斯力矩项引起的MT较小,Δφ为一小角度。
由式(20)可以看出,平衡攻角ΔD的方位在角度(φD+Δφ)的相反方向上,即在舵面法线方向φD相反的180°附近,相差一个小角度Δφ。
为了验证上述规律,以某大口径二维弹道修正弹为例,利用六自由度刚体弹道方程,设置操纵舵舵偏角FD0=6°,舵面压力中心到弹丸质心的距离lG=500 mm,控制时间为3 s,分析3 s内的弹轴运动规律。图10、图11分别给出了控制力向上、向下作用3 s内的攻角、速度偏角曲线。
由图10和图11可知,在固定方位φD舵控力长时间作用下,平衡攻角、平均速度偏角的方向与控制力方向近似成180°,相差一个小的角度Δφ。
图12、图13分别给出了全弹道上控制力向上、向下作用时的攻角、速度偏角曲线。

图10 控制力向上,3 s内的攻角曲线、偏角曲线

图11 控制力向下,3 s内的攻角曲线、偏角曲线
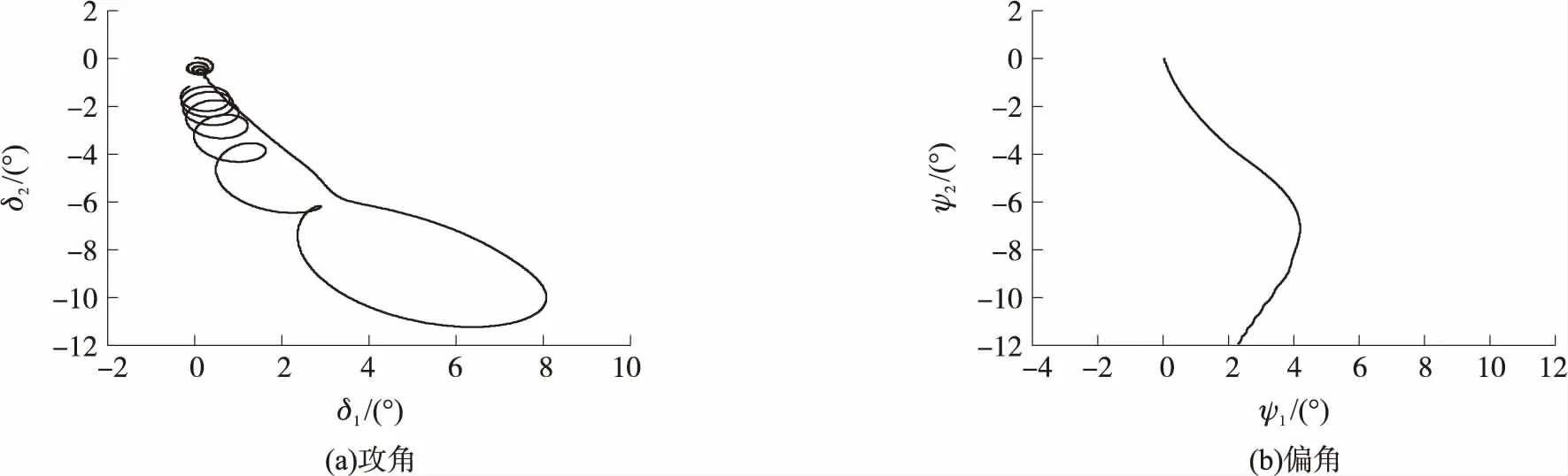
图12 全弹道控制力向上时的攻角、偏角曲线

图13 全弹道控制力向下时的攻角、偏角曲线
由图12和图13可知,在全弹道上固定方位舵控力作用下,弹丸的攻角运动规律是由舵控力产生相反方向的攻角与重力产生向右的动力平衡角合成的,平均速度偏角方向为该合成攻角的方向,该速度方向将影响弹道的质心运动,实现弹道修正。
4 结论

②弹丸在瞬时控制力作用下,产生的平衡攻角、平均速度偏角的方向与瞬时控制力方向大致相反;
③弹丸在固定方位舵控力长时间作用下,平衡攻角、平均速度偏角的方向与控制力方向近似成180°,相差一个小的角度Δφ;
④弹丸在全弹道上作用固定方位舵控力,弹丸的攻角运动是由舵控力产生相反方向的攻角与重力产生向右的动力平衡角合成的,平均速度偏角方向为该合成攻角的方向。

