高考数学试题研究的几种视角

（江苏省涟水中学 江苏淮安 223400）

一、研究试题的重要性

古人认为“书读百遍，其义自见”，才有今人的“题海战术”，这样造成我们一些同学在做一些比较新颖的题型时，感觉特别生疏，无从下手，这样的弊端正好暴露了我们学习的短板。我们经常会羡慕一些同学，他平时学习跟大家一样，该玩的时候玩，该学习的时候学习，但是一到考试时就考得特别好，有些下了很大功夫的学生反而成绩不怎么样，我就是这样的学生，有时我就在想，要是我也有跟他们一样的脑子，该多好！后来发现自己错了，大家都是“上帝咬过一口的苹果”，只要不是天生的愚笨，大家都是一样的，只是人家在学习的过程中是用心在学习，而我只是在完成一种任务，给自己强加了冗余的“砝码”，导致付出与收获不平衡。我开始去向学习好的同学取经，发现他们题做得不多，但是他们做得精，经常反思，不断研究试题，不光有了深度，还有了广度。从中领会了出题人的意图，直切试题实质，从而发挥试题功能的最大化，对于学习有了事半功倍的效果。[1]

二、研究试题的视角

针对不同的题型，我们都要有应对的“法门”，平时我们就要养成勤思勤问的学习态度，学会用“火眼金睛”去观察，透过现象看本质，以“变”对“万变”，把知识运用“活”了，才能受益终生。我根据自己平时关于学习数列总结下来的经验，以此为例，谈谈关于我们在解这类试题时该养成怎样的视角去研究。[2]

题目1：已知等比数列{an}的公比为q，记bn＝am（n－1）＋1＋am（n－1）＋2＋…＋am（n－1）＋m，cn＝am（n－1）＋1·am（n－1）＋2·…·am（n－1）＋m（m，n∈N*），则以下结论一定正确的是（ ）

A．数列{bn}为等差数列，公差为qm

B．数列{bn}为等比数列，公比为q2m

C．数列{cn}为等比数列，公比为qm2

D．数列{cn}为等比数列，公比为qmm

视角1 研究试题的立意

立意就是要知道出题人考查这道题需要涉及哪些知识点，哪些思想方法，要运用到哪些解题技能，来考察同学们的解题能力，以达到检测学生学习情况的目的。而针对本题，设计的考点是：①等比关系的确定；②等差关系的确定。只有熟练掌握等差数列与等比数列的定义、通项公式及其前n项和公式才是解题的关键。

视角2研究试题的解法

“条条大路通罗马”，只要我们的思路对，高考试题基本都可以一题多解，这样宽口径地考察同学，就需要我们在平时做题的时候，多积累解题方法，遇到这类题型脑海中就需要有一定的方式方法。既会有朴实自然的通法，又会有简捷的巧法，这既能培养我们的学习兴趣，又能培养我们思维的发散性、灵活性和深刻性，还能培养我们的数学探究意识，为我们的终身学习奠定基础。

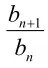
n＋1nn公比为q，利用等比数列的通项公式可得

得出即可判断出C，D两个选项．

视角3 研究解题的思想方法

每种题型都需要研究它的解题思想方法，这样我们在做题时才能广开思路，比如我们在解决三角函数这类题型，经常会用到数形集合思想、化归转化思想和分类讨论思想，三角函数是根据图像而建立的数学语言，所以我们在对任意角的三角函数研究都可以借助单位圆来进行转换。而对有关等比数列问题时，可用到下列的几种常见思想方法：

（1）方程的思想。等比数列中有五个量a1、n、q、an、Sn，一般可以“知三求二”，通过列方程（组）求关键量a1和q，问题迎刃而解。

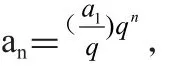
单调性：当或时，{an}是递增数列；

当或时，{an}是递减数列；

当q＝1时，{an}为常数列；

当q＜0时，{an}为摆动数列．

（3） 分类思想。当q＝1时，{an}的前n项和Sn＝na1；当q≠1时，{an}的前n项和Sn＝＝.等比数列的前n项和公式涉及对公比q的分类讨论，此处是常考易错点。

视角4 研究试题的变式

对于教学大纲中的知识点，出题中都会涉及到，而数学进行了这么多年的考试，为什么我们在刷题的过程中，难做到一模一样的原题呢？就在于它的多变性，所以研究试题的变式，可以发散我们的思维，不管试题怎样进行重组、引申、拓展，我们都可以找到它们发展的规律，让我们在不变中应万变。数学的魅力在于“变”，有“变”才有“用”，有“变”才能“活”。

通过对本题拓展研究，我们可以找到许多变式，下面给出一种常见的变式：

数列{an}满足a1＝1，nan＋1＝（n＋1）an＋n（n＋1），n∈N*.

（1）证明：数列是等差数列；

（2）设bn＝3n·，求数列{bn}的前n项和Sn.

本题考查利用等差数列的定义证明数列是等差数列；考查数列求和的方法：错位相减法。数列求和的关键是求出通项并选择合适方法，（1）将nan＋1＝（n＋1）an＋n（n＋1）的两边同时除以n（n＋1）得＝＋1，由等差数列的定义得证。（2）由（1）求出bn＝3n· ＝n·3n，利用错位相减求出数列{bn}的前n项和Sn.

在高考中，经常以解答题形式综合考查等差数列与等比数列的基本知识和基本方法，不管它怎样变化，我们只要把通用公式和数学方法记住，遇到此类题目我们都可以根据母题的发散思维去解题。