方程思想在解含三角形n等分线问题中的应用
(四川省内江天立(国际)学校 四川内江 641000)
方程思想贯穿中学数学始终.几何学科中求值问题常涉及利用方程思想解题,其核心解题思路是以所给条件为抓手、表示题中相关量、寻求等量关系、建立方程求解未知量.本文以“含三角形n等分线”为问题导向,以方程思想为解题主线,分别研究六类等分线问题,供读者参考.
类型1 三角形内角n等分线形成的角
例1 在△ABC中,∠A=α,∠ABC、∠ACB的n等分线分别交于点O1、O2、…、On-1,求∠BOn-1C的度数.(用α表示)
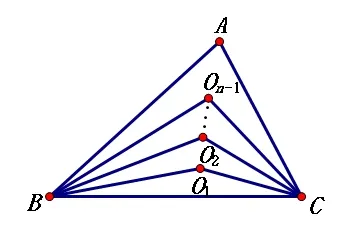
解析 因为∠ABC、∠ACB的n等分线分别交于点O1、O2、…、On-1,故令∠O1B C=∠O2B O1=∠O3B W2O=…=∠ABOn-1=x°,
∠O1C B=∠O2C O1=∠O3C O2=…=∠ACOn-1=y°,

点评:该问题实质上是求∠BOn-1C与∠A的数量关系,可借助“三角形内角和为180°”,利用方程思想分别将这两角放入△ABC和△On-1BC中研究,值得注意的是,解答时设元x、y但不求x、y的值,体现了整体代入消元、“设而不求”思想.另外,此题拆去边BC,立得类型2.
类型2 “规形图”n等分线形成的角
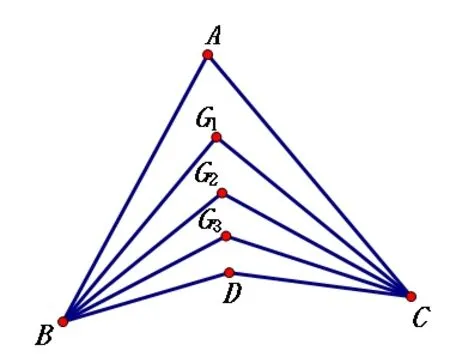
例2 如图,∠ABD,∠ACD的n等分线相交于点G1、G2…、Gn-1,若∠BDC=α,∠BG1C=β,求∠A的度数.(用α、β表示)
分析
此题解法类似例1,抓住∠B GiC=∠ABGi+∠ACGi+∠BAC,利用方程思想,
类型3 三角形外角n等分线形成的角
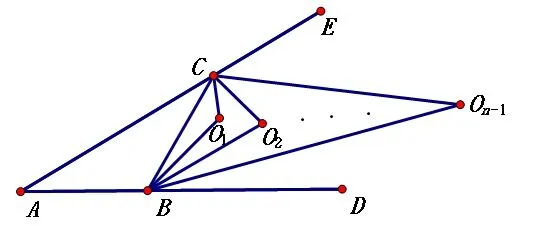

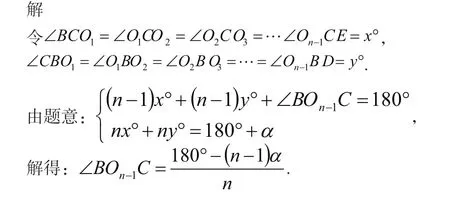
点评:此题与上题类似,类比推理可得.
类型4 三角形内角n等分线和外角n等分线形成的角
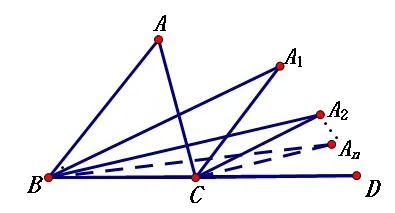
例4 如图,在△ABC中,∠A=α,∠ABC和∠ACD的平分线交于点A1,得∠A1;
∠A1BC和∠A1CD的平A分线交于A点A2,得A∠A2;∠AnBC和∠AnCD的平分线交于点n,得∠n,求∠n的度数.(用α表示)
解析 令∠ABA1=∠A1B C=x°,∠ACA1=∠A1C A2=y°,
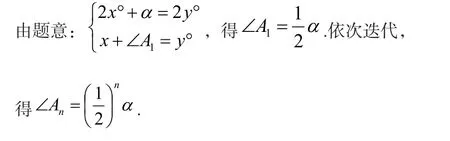
点评:本例与前3例有所不用,体现在反复利用迭代思想或观察规律求∠An.此题常作为考试选择、填空中压轴试题.
类型5 折线“8字”型n等分线形成的角
例5 ∠BAD的平分线AE1与∠BCD的平分线CE1交于点E1,∠BAE2的平分线AE2与∠BCE2的平分线CE2交于点E2,......,∠BAEn的平分线AEn与∠BCEn的平分线CEn交于点En,则∠AEnC与∠ADC、∠ABC之间是否仍存在某种等量关系?若存在,请写出你得结论,并给出证明;若不存在,请说明理由。
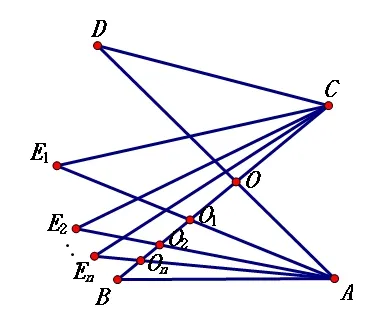
解析 折线“8字”型问题,要抓住(以此题为例)
∠ADC+ ∠DCB=∠ABC+∠DAB
这一等量关系解题.此题不妨令∠DCB=x°,∠DAB=y°,
则∠ABC-∠ADC=x°-y°.
由CE1平分∠BCD,AE1平分∠BAD,

类型6“ M ”型n等分线形成的角
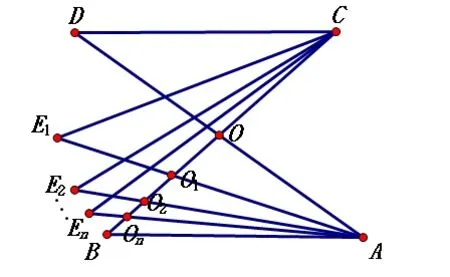
例6 如图,AB∥CD,∠BAD的平分线AE1与∠BCD的平分线CE1交于点E1,∠BAE2的平分线AE2与∠BCE2的平分线CE2交于点E2,......,∠BAEn的平分线AEn与∠BCEn的平分线CEn交于点En.判断并说明∠AEnC与∠ADC、∠ABC之间存在的数量关系.
分析:解法同上题,答案略.
点评:“M ”型n等分线形成的角与折线“8字”型n等分线形成的角具有相似之处,可类比推理分析问题.
以上所述6类“含三角形n等分线形成的角”仅为单一命题形式,常见地还有以组图形式、问题串形式等考查学生思维,方程思想方便之处在于简化角的书写表达,便于分析问题.教学时教师需注重引导学生将复杂问题简单化、简单问题条理化.

