例谈学生直观想象核心素养的提升

（山东省乳山市第二中学 山东乳山 264500）

众所周知，立体几何教学有自身独特的特点与需求，在教学中，既需要教师有过硬的专业素养，还需要有较好的创设、引导几何空间想象能力；对学生来将，需要扎实的计算基础，更需要良好的空间想象能力。因此，立体几何教学成为高中数学教学的难点。但立体几何是高考试题的重要组成部分，更是培养学生数学核心素养中不可或缺的内容。我们必须优化当前高中立体几何教学，真正实现高中立体几何教学有效性的提升。[1]

一、建模用模，提升学生直观想象能力素养

1．建模：建模是几何思维培养的第一步，就是通过具体的模型，先在学生脑子中形成“初印象”在后面的学习中才有可能“再创造“，我们可以利用的模型有学校统一定制的教师演示模型，它的缺点是教师演示，学生参与少，难以发挥其真正作用，所以在建模中我更推崇的是利用手边就地取材的模型：桌面、书本、手掌、笔、手指、教室的墙角、粉笔盒等等。善用这些现成的模型，可以使许多问题变得比较直观，让学生在真正参与中把问题解决掉。[2]

案例1：在讲授《1.2.2线面平行》这一节时，我们设计探究问题如下：

问题1（粗观察）：大家打开课本，当我们在翻动时，你会发现翻动页边所在的直线与其它页所在的平面有什么特点？（设计开放性问题，开阔学生思维）[3]

问题2（细探究）：

（1）翻动页两边所在的直线有什么样的位置关系呢？

（2）当课本合上的时候课本转动的一边与平面是否还是平行关系？

（3）如果要让线与面平行的话要保证什么条件？

引导学生借助手中现成的工具----课本，让学生在“观察----尝试----收获“中，直观了解线面平行，学生在打开课本比划中，掌握线面平行的判定定理，这一教法提高了学生的学习兴趣，帮助学生发现数学原理，培养了他们的空间想象能力。[4]

2．用模：用模型就是学生根据自己对于具体模型的特点的熟知，把不熟悉的几何体（或是难解决的）放在熟悉的几何体模型中来解题的一种思维方法。我们在遇到几何体的外接球有关问题时，往往借助长方体这个神奇的模型来解决，下面我们来看一类外接球类型：

案例2：当四面体的对棱相等时，我们可以把它看成是长方体切割而来，对棱长全相等的正四面体可以看成正方体切割而来。

例题：（2013包头模拟）如图所示，在等腰梯形ABCD中，AB=2DC=2，∠DAB=600，E为AB的中点，将ΔADE与ΔBED分别沿ED，EC向上折起，使A，B重合，则形成的三棱锥的外接球的表面积为_____________________

分析：本题的关键是定型，才能应用相关的结论进行解题，由已知条件知，平面图形AE=EB=BC=CD=DA=DE=EC=1，折叠后得到一个正四面体，如图所示把正四面体放置在正方体中：

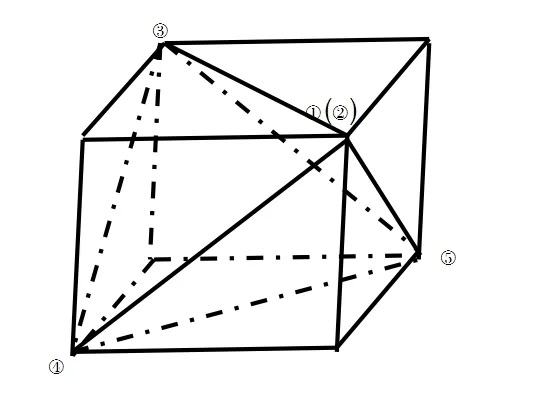
二、创设实践活动的机会，提升学生直观想象能力素养

以学生为主体，在坚持学生在教学中主体地位，充分发挥学生主动性的基础上进行教学方式的创新。定理的教学是立体几何中的难点，众所周知物理和化学都有实验课，为何我们不把数学“实验”引入课堂，他们会有异曲同工之妙的。

当下流行的教学方法创新实践，很多都已经取得了较为理想的效果，如翻转课堂教学，这一教学方式具有极高的整体性与系统性，较为适合立体几何的教学。在实际开展中，教师在课堂教学之前将学习素材以视频、图像等形式上传到教学平台，学生通过教学平台进行课前预习，因而能减少一部分不必要的课前教学，增加了有效课堂教学时间；在课堂教学中，教师将课堂可以交给学生，以学生合作探究、自主思考等方式主动探索教学内容，教师只需要在最后进行总结与深化，学生通过自己的努力得来的知识与能力一定比教师灌输更加灵活与深刻，在这一过程中，学生的空间想象能力与学习能力也得到了发展。课后巩固阶段，教师将相应的练习题上传至平台，学生在练习时遇到问题可以在教学平台留言，教师在之后的教学中重点进行弥补，这样一个教学闭环就形成了，既保证了学生的主体地位，又能够很好的提升教学质量。

三、数与形的完美结合，提升学生直观想象能力素养

新课标下，考试中心对考试大纲的说明中强调：“在高考中，充分利用选择题和填空题的题型特点，为考查数形结合的思想提供了方便，能突出考查考生将复杂的数量关系转化为直观的几何图形问题来解决的意识。”“数”与“形”结合，相互渗透，就是把代数问

所以，外接球的表面积为题几何化，在形中轻松解决繁琐的代数问题，这也是高考考察的重要数学思想之一。

结语

高中立体几何教学的进步，需要教师切实提高专业素养与教学技能，以先进的教学理念引导教学的开展，对教学方式进行切实可行的优化创新，发挥自身主动性充实丰富教学方法，做到全方位保证教学质量的提高。