“定积分存在的条件”问题情境教学设计
——从Riemann函数看Riemann积分
(湖南城市学院理学院 湖南益阳 413000)
一、内容分析
定积分是理解《数学分析》积分理论的基石,教材[1]先阐述了达布和的定义和性质,在此基础上证明了定积分存在的第一和第二充要条件。我在教学中利用定积分存在的两个充要条件归纳总结了Riemann函数的一些性质,在此基础上精心创设具有探究性、开放性的问题情境,让学生产生必要的认知冲突,有效调动学生积极思维,主动参与认知的发现过程,引导学生不断提出问题,澄清了一些错误理解,证明了R可积函数类的一些深刻性质,为学生学习广义积分、重积分、复积分和实分析打下了基础。
二、教学设计
1.利用复习环节作好铺垫。
从宏观上分析定积分存在的第一和第二充要条件的内在联系,阐述第一充要条件与第二充要条件的应用方法,为Riemann函数R可积的证明作准备。
复习:
几个记号:
分划:

(1)复述定积分存在的两个充要条件。
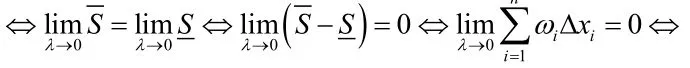
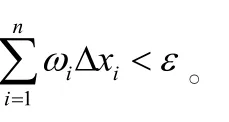
推论1 有界函数f(x)在[a,b]上R可积的充分必要条件是:对∀ε>0,存在分划Δ,

定理2(定积分存在的第二充分必要条件)有界函数f(x)在[a,b]上R可积的充分必要条件是:对任意给定的两个正数ε>0及σ>0,可找到δ>0,使得当任一分法满足λ(Δ)<δ时,对应于振幅ωi'≥ε的那些区间Δxi'的长度之和∑Δxi'<σ。
推论2 有界函数f(x)在[a,b]上R可积i'的充分必要条件是:对任意给定的两个正数ε>0及σ>0,存在一分法Δ,对应于振幅ωi'≥ε的那些区间Δxi'的长度之和Δxi'<σ。
(2)这两个充要条件之间有何内在联系?
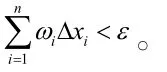
(3)如何应用这两个充要条件讨论函数的可积性?
证明所有ωi一致小于ε,如连续函数可积性的证明;
推论3:若f(x)在[a,b]上连续,则对∀ε>0,总可在[a,b]上插入若干分点,使得f(x)在每个小区间上的幅度ωi<ε。
证明n所有Δxi一致小于ε,如单调有界函数的可积性的证明;
将∑i=1ωiΔxi分成两部分,一部分ωi能一致小于ε,另一部分虽然ωi不能一致小于ε,但其区间长度的和能一致地小于σ,如只有有限个不连续点的有界函数的可积性的证明。
推论4:若f(x)在[a,b]上R可积,且积分值为I,又f∗(x)是f(x)在有限个点改变函数值后得到的函数,则f∗(x)在[a,b]上也R可积,且积分值仍为I。
2.改变教材的呈现方式,将命题分解为若干个前后呼应,环环相扣的小问题,把教材冰冷的美丽变为学生火热的思考。
例。定义Riemann函数
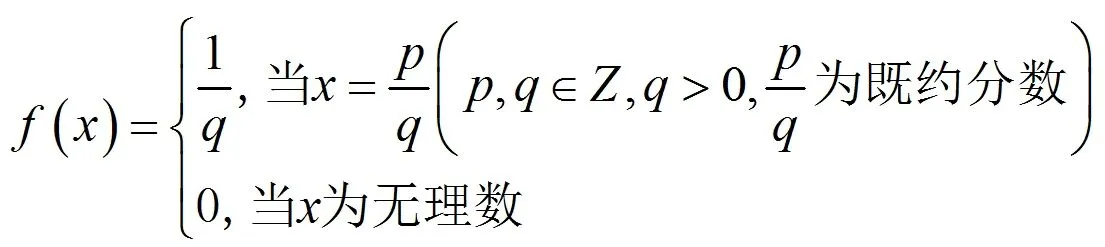
证明:
(1)对ε>0,在任意有限区间[a,b]上使f(x)≥ε的点x只有有限多个。
(2)f(x)在任意一点的极限都为0。
(3)f(x)在所有无理点处连续,有理点处不连续。
(4)f(x)在任意有限区间[a,b]上都R可积,且积分值为0。
(5)f(x)没有原函数,从而R可积函数不一定有原函数。
3.巧妙设问,层层深化,引导学生深入思考,领略积分世界的新天地。
接上文,问:什么样的函数会没有原函数呢?
(6)含有第一类间断点的函数一定没有原函数。问:知道了f(x)的原函数是F(x)之后,
引导学生发现:上式左边积分不一定存在。这是因为
(7)有原函数的函数不一定R可积。

从而f(x)在含有0的区间[a,b]上无界,从而在[a,b]上不R可积。
问:我们知道含有第一类间断点的函数一定没有原函数,那么含有第二类间断点的函数是不是也一定没有原函数呢?
引导学生发现,由上例可知:
(8)含有第二类间断点的函数可以有原函数。

引导学生发现,此时不能套用牛顿-莱布尼兹公式,因为牛顿-莱布尼兹公式的条件是f(x)连续,但是牛顿-莱布尼兹公式可以推广为:
(9)若f(x)有原函数F(x),且在[a,b]上R可积,
问:什么样的函数既有原函数又R可积呢?
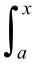
问:只有有限个间断点的有界函数是R可积的,那么有无限个间断点的有界函数R可积吗?
引导学生由Riemann函数和Dirichlet函数不难发现:
(11)在[a,b]上有无限个间断点的有界函数可能R可积,也可能不R可积。
问:在[a,b]上有无限个间断点的有界函数在什么条件下会一定R可积呢?
(12)若在[a,b]上的有界函数有无穷多个间断点,但这无穷多个间断点只有唯一的聚点,则该函数在[a,b]上R可积。
问:若在[a,b]上的有界函数有无穷多个间断点,但这无穷多个间断点有有限个聚点,则该函数在[a,b]上R可积吗?
引导学生发现,由积分的区间可加性可知:
(13)若在[a,b]上的有界函数有无穷多个间断点,但这无穷多个间断点只有有限个聚点,则该函数在[a,b]上R可积。
问:若在[a,b]上的有界函数有无穷多个间断点,但这无穷多个间断点有无穷个聚点,则该函数在[a,b]上R可积吗?
引导学生由Riemann函数和Dirichlet函数可知
(14)若在[a,b]上的有界函数有无穷多个间断点,但这无穷多个间断点有无穷个聚点,则该函数在[a,b]上未必R可积。
4.引导学生对以上有关结论给出严格证明。证明追求严谨,但不拒绝形象直观。结合图形阐述有关证明思路,从而使推理深入浅出。
5.构造具体实例,帮助学生理解上述相关结论。
例 判断下列函数在[0,1]上是否R可积。
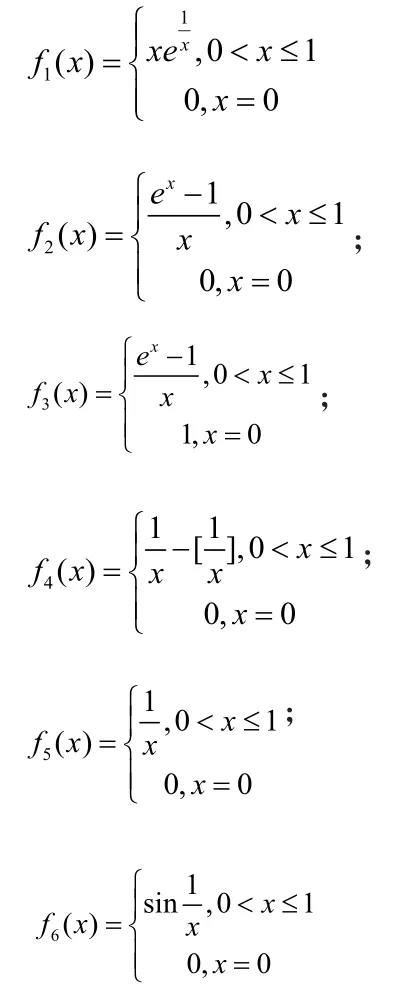
在引导学生思考“从间断点的多少的角度看,在[a,b]上的有界函数R可积有何充要条件?”的问题时,可告诉学生:实变函数理论告诉我们
6.适当拓展,激发学生的求知欲。
设f(x)在[a,b]有界,则f(x)在[a,b]上R可积的充要条件是f(x)在[a,b]几乎处处连续,即f(x)在[a,b]的间断点构成零测度集,形象地说,其间断点不“很多”。
又如:Dirichlet函数在[a,b]上不R可积,但改变积分的定义方式,如在勒贝格积分的意义下它又是可积的,此时称L可积。
结语
从Riemann函数的几个常用结论出发,精心设计了一系列环环相扣的问题情境,引导学生始终处于问题的探索与求真的过程中,证明与反例相结合,帮助学生厘清了一此似是而非的错误理解,将对定积分的理解上升到一个新的高度。更重要的是,学生在积极参与知识的探索过程中培养了发现问题、提出问题的可贵的科学品质和创新精神。

