分数阶带捕获的Lotka-Volterra生物经济模型演化研究

胡行华，高雷阜,李莉莉

（1.辽宁工程技术大学 理学院；2.阜新高等专科学校 计算机信息技术系,辽宁 阜新 123000）

1 问题的提出

在经济社会高速发展的今天，自然资源和生态环境经常遭到破坏，濒危种群的种类也在逐年递增，有关资源短缺和环境恶化方面的问题广受关注。从人类的物质需求和经济需求来看，对各种各样生态资源的开采和种群生物的捕获是不可避免的。但是，肆意的开采和捕获会造成自然资源和环境的破坏，同时使得濒危物种的数量逐年递减。因此，在保护好生态环境和达到资源持久再生的前提下，如何控制开采和捕捞的数量，使资源开发管理达到经济利益最大化是一项重要的研究课题[1]。

资源更新的最优管理直接关系到资源的可持续性发展，不仅能够更加丰富现有的理论研究，而且更好的协助于保护生态资源，在生物学和经济学两方面都具有重大意义。利用系统动力学理论[2]来研究生物数学中的种群演化发展，在可再生资源的生态方面和经济方面的综合研究引起了许多学者的关注[3，4]，特别是，带捕获的Lotka-Volterra生物经济模型[5，6]在维护生态种群平衡问题上起到了相当大的作用，文献[7]研究了一类只对捕食种群进行捕获的捕食一食饵两种群模型，分析了平衡点的存在性和稳定性，得到了最优捕获策略；文献[8]研究了食饵种群在一类非线性密度制约下，两种群均有非常数收获率的捕食系统，利用微分方程定性与稳定性理论及分支理论，得到系统平衡点的性态，利用Hopf分支理论得到存到多个极限环的充分条件；文献[9]利用微分代数方程理论研究了一类广义生物经济系统的混沌及混沌控制问题，通过利用反馈线性化方法设计控制器，使受控混沌系统的输出跟踪期望的恒值或某一期望的周期轨道，可以使处于混沌状态的生物种群平稳增长，实现生物种群的稳定演化和可持续捕捞。

经典的捕食食饵模型是如下的Lotka-Volterra模型[10]：

其中，x和y分别表示了在t时刻食饵种群的密度、捕食种群的密度，a为食饵种群的固有增长速度，k为食饵种群密度的制约系数（或者是食饵种群的死亡率），d为捕食种群的死亡速度，b为捕食种群的捕食强度。

在模型（1）的基础上把捕获的经济收益考虑进去可以得到带捕获的Lotka-Volterra模型[10]：

其中，E为捕获强度（如出海时间，拥有船只数量等，通常设定0≤E≤1），p为单位食饵捕获的报酬，c为捕获花费，v为经济效益。

带捕获的Lotka-Volterra生物经济模型是人类参与的包含许多主体因素的极其复杂的非线性系统，由于模型的部分变量具有长期的记忆性，运用整数阶微积分理论不能描述其变化特性，因而，需要尝试运用分数阶微积分理论建立其非线性动力学模型[11，12]，同时利用系统平衡点的稳定、分岔、混沌等方面的理论来研究模型的内在复杂性。本文在提出模型（2）的分数阶代数-微分系统的同时，定性分析该分数阶系统平衡点的稳定性、Hopt分岔、混沌等产生的条件，并运用Block-by-Block算法，通过时间序列图、相图等对带捕获的Lotka-Volterra模型复杂性演化路线进行仿真研究。

2 算法描述

2.1 分数阶带捕获的Lotka-Volterra模型描述

本文对分数阶导数的定义采用如下Caputo定义形式[13]：

其中，n-1＜α≤n，Γ(·)是Gamma函数。

下面给出系统（2）的分数阶形式：

其中，0＜β＜1，特殊地，当β=1，则分数阶带捕获的Lotka-Volterra模型（3）可以退化为整数阶带捕获的Lotka-Volterra模型（2）。

2.2 Block-by-block算法描述

考虑如下分数阶常微分方程组：

满足初始条件：

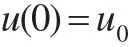
其中，u(t)=(u1(t)，u2(t)，…，um(t))，F=(f1，f2，…，fm)，0用α阶Caputo分数阶导数定义。则方程组与下面的Volterra积分方程是等价的：

其中，Γ(·)表示Gamma函数。

由Kumar和Agrawall构造的block-by-block算法[14]如下：将区间[0，T]分成2N个等分的子区间，其中：，设tj=jΔt，j=0，1，，2N。记方程在点tj上的数值解为uj，并记Fj=F(tj，u(tj))，假设已经构造出uj，j=0，1，…，2m，则逼近u(t2m+1)和u(t2m+2)的方法如下：

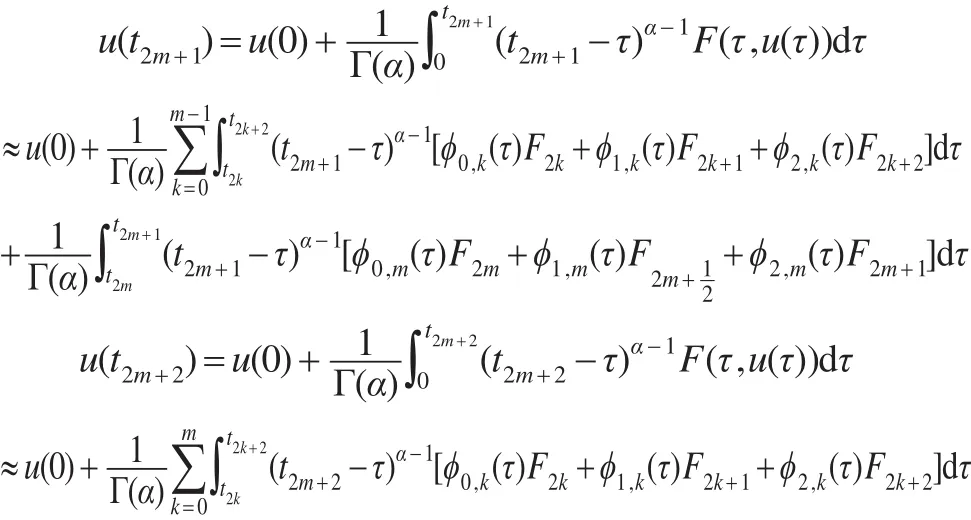
其中，ϕi，k(t)，i=0，1，2;k=0，1，…，m和ϕi，m(t)，i=0，1，2为分别定义在点上的二次拉格朗日插值基函数，并且

3 系统平衡点的稳定性分析

为了求系统（3）的平衡点，首先由系统（3）的代数方程可以得到代入到微分方程的右端可以得到系统（3）的平衡点满足方程组：

解方程组（5）可以得到系统（3）的平衡点为：P1=(0，0)，，由于P1、P2都是极端平衡点（退化平衡点），不利于生态资源的均衡演化。在此主要研究平衡点P3的渐近稳定、Hopt分岔、混沌演化等发生的条件。

在平衡点P3处系统的Jacobian矩阵为：

解得：

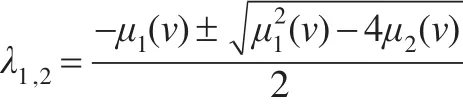
由于μ2(v)＞0，所以有：

（1）当μ1(v)＞0，即时，系统的所有特征值具有严格负实部。此时，平衡点P3是渐近稳定平衡点；

（2）当μ1(v)=0，即时，系统的特征值是一对共轭纯虚根，并且满足Hopt分岔条件，此时，系统在D(V，δ0)产生Hopt分岔；

（3）当μ1(v)＜0，即时，系统的特征值具有正实部。此时，平衡点P3是不稳定平衡点，会发生混沌等不确定现象。

4 系统演化仿真

下面对系统（3）在平衡点P3附近的演化规律进行研究，对于确定的带捕获的Lotka-Volterra模型，其分数阶微分系数β已经惟一确定，从而本文仅针对经济效益v的变化对系统（2）的复杂性演化影响进行仿真。以Matlab2015a为操作平台，在Intel（R），Pentium（R），Core(TM)i7-3520M CPU，2.9 GHz，4.00 GB内存，Windows7操作系统上执行Block-by-Block算法[13]。

根据模型的实际意义，取系统一组参数为：a=4,k=1,d=2,p=1,c=1；同时取微分阶数β=0.95，通过上述系统（3）在平衡点P3附近的演化稳定性分析可以得到：

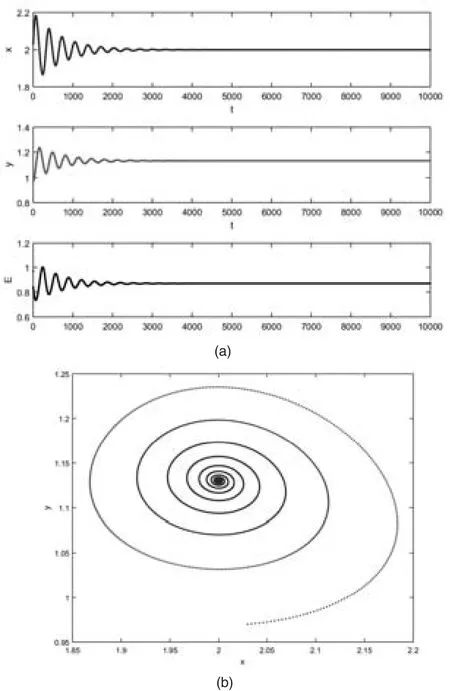
图1 经济效益v=0.87时,图(a)系统（3）各分量演化序列图,图(b)系统（3）演化的相图

通过理论分析和图1可以得出，在此组参数条件下，随着系统的演化，捕食种群和食饵种群的数量会在P3维持一个稳定的状态。此时，捕获者、捕食种群和食饵种群可以长久共存下去，捕获者可以获得相应的的最大经济效益，有利于生态资源的合理利用和健康发展。

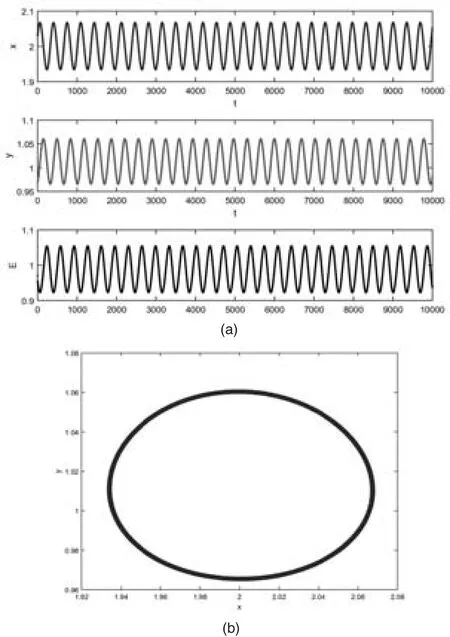
图2 经济效益v=0.999849时,图(a)系统（3）各分量演化序列图,图(b)系统（3）演化的相图

通过理论分析和图2可以得出，在此组参数条件下，随着系统的演化，捕食种群和食饵种群的数量会在P3产生Hopt分岔，系统呈现出周期性变化规律，不利于系统的发展和生态资源的稳定。

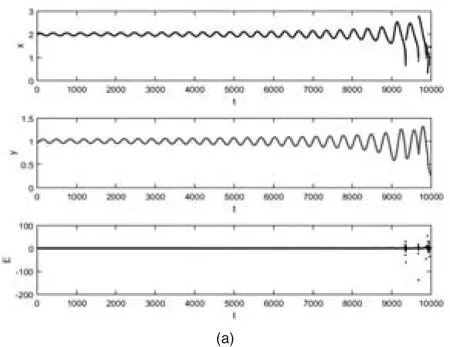
图3 经济效益v=1.01113时,图(a)系统（3）各分量演化序列图,图(b)系统（3）演化的相图

通过理论分析和图3可以得出，在此组参数条件下，随着系统的演化，捕食种群和食饵种群的数量会在P3产生混沌等不确定现象，无法对该系统的演化发展作出预测，同时整个系统处于处于一种失控状态，会产生非常大的破坏作用，不利于系统的发展和生态资源的稳定。

5 结论

混沌和分岔是非线性动力系统的一种内在不确定性的体现，是经常出现在非线性系统演化中的一种极其复杂的现象，是非线性系统稳定演化之外的典型形式；控制和避免混沌、分岔等现象才能有利于系统的稳定发展和精确预测。本文在给出分数阶带捕获的Lotka-Volterra生物经济系统基础上，从理论上分析了系统部分平衡点附近渐近稳定状态、分岔状态以及混沌状态的发生条件，同时运用Block-by-Block算法，通过时间序列图和相图等作了捕获者经济利益的变化对系统演化规律的影响数值仿真，得到了食饵种群持久生存前提下捕获者的最大经济效益。可以为生物资源的稳定发展和持续捕获提供理论依据。