具有恐惧效应的离散捕食者-食饵模型的稳定性*

舒 晴，谢景力，刘晗嫣

(吉首大学数学与统计学院，湖南 吉首 416000)

在生物数学中，捕食者与食饵之间的相互关系是学者研究的重点.最早的捕食者-食饵模型是Lotka-Volterra模型[1-2].1960年，Leslie等[3]认为捕食者种群的数量取决于捕食者与食饵的比率，并给出了Leslie-Gower模型.一些学者通过研究捕食行为建立了功能反应的概念,功能反应描述了每个捕食者单位时间内消耗的食饵数量[4-5].

在生物学中，一些因素会对种群数量造成影响,于是越来越多的学者致力于研究这些因素对捕食者-食饵模型稳定性的影响.有学者认为食饵对捕食者的恐惧会改变食饵的一些行为和生理特征，从而提出恐惧效应，它反映了食饵种群对捕食者种群的反捕食能力[6].为了在不影响种群繁衍的基础上获得最大的经济效应，学者在捕食者-食饵模型中加入1个收获项.受市场需求、成本等因素影响，收获项一直采用常数收获是不合理的,因此笔者考虑引入常数能力收获[7-10]，它比常数收获更具有指导意义,且便于计算.

连续和离散时间模型是描述种群关系的2类常用模型.当种群世代不重叠或数量很少时，离散时间模型是较合适的研究工具[11]，通过它可得到比连续时间模型更复杂的动力学性质，如混沌[12-13].笔者拟在经典Leslie-Gower模型的基础上,讨论恐惧效应和常数能力收获对新的离散Leslie-Gower模型的动力学性质的影响.

1 模型的建立

通过引入了常数能力收获和恐惧效应，建立如下具有Holling-Ⅱ型功能反应的修正的Leslie-Gower模型：

(1)

其中：x,y分别为食饵种群和捕食者种群的密度；r1,r2分别为食饵种群和捕食者种群的增长率；β为食饵种群内部的竞争强度；c1,c2分别为食饵种群和捕食者种群的人均减少率最大值；k1为环境对食饵种群和捕食者种群的保护程度；k为食饵种群的反捕食能力;E为收获能力；r2>E.

令

经过变换,模型(1)可以转化成

(2)

对模型(2)进行离散，可得

(3)

2 预备知识

从生物学的角度，当给定模型(3)的任一初始值u0=u(0)>0,v0=v(0)>0时，模型(3)的解un,vn均大于0.

定义1设λ1,λ2是F(λ)=0的根:

称平衡点E(x,y)是渐近稳定的，如果|λ1|<1,|λ2|<1；

称平衡点E(x,y)是不稳定的，如果|λ1|>1,|λ2|>1；

称平衡点E(x,y)是鞍点，如果|λ1|<1,|λ2|>1，或者|λ1|>1,|λ2|<1；

称平衡点E(x,y)是非双曲的，如果|λ1|=1，或者|λ2|=1.

引理1[14]特征行列式F(λ)=λ2-tr(J)λ+det(J)的解λ1,λ2满足|λ1|<1,|λ2|<1，当且仅当模型(3)的正平衡点是渐近稳定的，且|tr(J)|<1+det(J)<2.

3 平衡点的存在性

为了找到模型(3)所有的平衡点,根据差分方程平衡点的概念,需要解出如下模型：

(4)

φ2u2+φ1u+φ0=0

(5)

的正实数根.这里：

φ2=df(γ-p)；φ1=dfs(γ-p)+d(γ-p)2+f2；φ0=ds(γ-p)2+f(γ-p)-f2.

对于模型(3),零平衡点E0(0,0)与轴平衡点E1(1,0)是恒存在的.

定理1当γ-p>0且ds(γ-p)2+f(γ-p)0,φ1>0,φ0<0.

证明设二次方程(5)的根为m,n,根据根与系数的关系可得

因为r2>E,所以γ>p,于是

φ1=dfs(γ-p)+d(γ-p)2+f2>0,φ2=df(γ-p)>0.

证毕.

4 平衡点的稳定性

模型(4)的雅可比矩阵

其中

定理2(1)当且仅当γ>p时，平衡点E0(0,0)是不稳定的.

(2)当且仅当γ

(3)当且仅当γ=p时，平衡点E0(0,0)是非双曲的.

证明在平衡点E0(0,0),矩阵J(0,0)的特征值λ1=e>1,λ2=eγ-p.根据定义1可得下列结论:

(1)当eγ-p>1即γ>p时,平衡点E0(0,0)是不稳定的.

(2)当eγ-p<1即γ

(3)当eγ-p=1即γ=p时,平衡点E0(0,0)是非双曲的.

证毕.

定理3(1)当且仅当γ

(2)当且仅当γ>p时，平衡点E1(1,0)是鞍点.

(3)当且仅当γ=p时，平衡点E1(1,0)是非双曲的.

证明在平衡点E1(1,0),矩阵J(1,0)的特征值λ1=0,λ2=eγ-p.根据定义1可得下列结论:

(1)当eγ-p<1即γ

(2)当eγ-p>1即γ>p时,平衡点E1(1,0)是鞍点.

(3)当eγ-p=1即γ=p时,平衡点E1(1,0)是非双曲的.

证毕.

在平衡点E2(u1,v1)，令

F(λ)=λ2-tr(J)λ+det(J)=λ2-(2+M)λ+(1+M+N)，

其中

定理4设λ1,λ2是F(λ)=0的根，则模型(4)的正平衡点E2(u1,v1)是渐近稳定的当且仅当|2+M|<2+M+N<2.

证明因为tr(J)=2+M,det(J)=1+M+N,所以根据引理1可得模型(4)的正平衡点E2(u1,v1)是渐近稳定的当且仅当|2+M|<2+M+N<2.证毕.

5 正平衡点的Flip分岔

P(λ)=λn+d1λn-1+…+dn-1λ+dn,

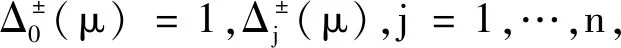
如果如下条件满足，那么Flip分岔发生在μ=μ0：

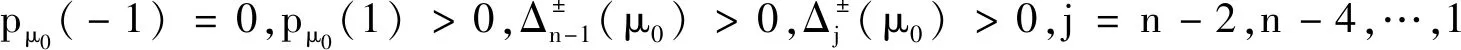
如果选择f为分岔参数，那么根据引理2可得如下结果：

定理5若

1-C1+C0=0,1+C1+C0>0,

其中C1=-(2+M)，C0=1+M+N，则模型(4)在正平衡点E2(u1,v1)经历了Flip分岔.

6 数值模拟

选取参数值d=2.1,s=0.16,f=11.8,γ=4.55,p∈[1.2,2.4],初值(u0,v0)=(0.553,0.148 8).可以观察到,当p=2.086 59时，模型(4)有唯一的正平衡点E2(u1,v1)=(0.553 07,0.148 863 9)，且模型(4)经历了Flip分岔.显然，定理5中的所有条件都满足，即

1-C1+C0=0,1+C1+C0=1.709 121 6>0,

1+C0=0.854 56>0,1-C0=1.145 439>0,

模型(4)在正平衡点E2(u1,v1)的Flip分岔如图1所示.

图1 Flip分岔Fig. 1 Flip Bifurcation

由图1可见,当p>2.086 59时,正平衡点E2(u1,v1)是渐近稳定的；当p<2.086 59时,正平衡点E2(u1,v1)会失去稳定性.这说明,适当地增加捕食者的收获可以稳定系统.