求解无约束函数局部鞍点的数值算法
吕义勇, 赵文杰, 周光明
(湘潭大学 数学与计算科学学院, 湖南 湘潭 411105)
0 引言
鞍点问题是一个非常重要的优化问题, 可应用于许多研究领域, 比如对偶理论、最大最小优化等.目前已经有大量研究鞍点问题的文献.例如, Bertsekas等[1]对鞍点问题的基本理论进行了详细介绍.Benzi等在文献[2]中提出了求解线性系统类型的鞍点问题的迭代方法,在文献[3-7]中提出了几种迭代方法与预处理方法来求解鞍点形式的线性系统问题.对于求解凸-凹型目标函数的鞍点问题, 目前的方法主要利用梯度, 次梯度, 变分不等式[8-10].Vasilyev等[11]提出了一种外梯度方法, 用于找到线性常微分方程的受控系统解上定义的凸-凹函数的鞍点.郭晓等[12]对带有简单凸集约束的鞍点优化问题, 提出了投影原始-对偶梯度方法, 并证明了算法的收敛性.
近年来, 在求解非凸-凹型目标函数鞍点问题上取得了重要的进展, 多种求解该类型的鞍点问题的数值方法被提出了.2018年, 基于Lasserre松弛方法, Nie等[13]提出了一种计算多项式鞍点的数值算法, 并证明了算法的收敛性.该方法不要求目标函数是凸-凹的, 约束集也可以是非凸的.2019年, Zhou等[14]基于Lasserre松弛方法和最优性条件, 提出了计算一般约束下有理函数鞍点问题的数值算法, 并且通过数值实验验证了算法的有效性.以上文献讨论的鞍点都是全局鞍点, 目前, 对于局部鞍点问题的研究很少.2019年, Adolphs等[15]定义了局部鞍点.2020年, 赵文杰[16]基于最优性条件和Lasserre半定松弛方法, 提出了一种计算无约束多项式的局部鞍点的算法.
本文将讨论无约束局部鞍点的计算问题.考虑到若函数在无穷远处还有局部鞍点, 则在实际计算中,无穷远处的局部鞍点是很难计算的.因此, 为了计算方便, 在一个有界的区域(通常取盒子形状的区域)内讨论局部鞍点.
本文在第二部分提出求解无约束局部鞍点的数值算法和验证局部鞍点是否是全局鞍点的算法, 在第三部分对这两个数值算法进行收敛性分析, 接着在第四部分给出一些具体的数值实验去验证算法的有效性, 最后对论文进行小结.
1 求解局部鞍点的数值算法
先给出鞍点的定义[1], 该定义实际上也是本文所提到的全局鞍点的定义.
定义1.1令X⊆Rn,Y⊆Rm,若f(x,y)在点(x*,y*)∈X×Y处满足
f(x*,y)≤f(x*,y*)≤f(x,y*), ∀(x,y)∈X×Y,
(1)
则称(x*,y*)为f(x,y)在X×Y上的鞍点.
下面是局部鞍点的定义[15].
定义1.2令X⊆Rn,Y⊆Rm, 若存在很小的正数γ, 在点(x*,y*)∈X×Y处满足
f(x*,y)≤f(x*,y*)≤f(x,y*), ∀(x,y)∈[X∩B(x*,γ)]×[Y∩B(y*,γ)],
(2)
其中
(3)
则称(x*,y*)为f(x,y)在X×Y上的局部鞍点.
设f(x,y)在Rn×Rm上是二阶连续可微的, 假设定义1.1中的X=Rn,Y=Rm, 本文主要讨论目标函数f(x,y)在Rn×Rm上的局部鞍点的计算问题, 当计算出局部鞍点之后, 若f(x,y)在Rn×Rm上存在全局鞍点,将从局部鞍点的集合中选出全局鞍点.如果目标函数在无穷远处还有局部鞍点, 则在实际计算中, 无穷远处的局部鞍点是很难计算的.为了方便计算, 将在一个有界的区域内讨论局部鞍点.本文令定义1.1和定义1.2中的X=[l1,b1]n⊆Rn,Y=[l2,b2]m⊆Rm.其中,l1,l2,b1,b2是给定的常实数.
假设f(x,y)∈C2(X×Y)在X×Y上不同的局部鞍点值只有有限个, 其大小顺序排列如下:
现在提出求解局部鞍点的算法.
算法1
步0:给定邻域半径γ, 区域X=[l1,b1]n⊆Rn,Y=[l2,b2]m⊆Rm, 初始点(x0,y0)∈X×Y,令S:=∅.
步1:求候选局部鞍点和对应的函数值f*.
(a) 求解如下问题:
(c) 若C2为空集, 则目标函数在X×Y上不存在局部鞍点, 算法终止.

(a) 给定初始点x0, 求解如下问题:
(4)
得最优解集为Cx={x1,x2,…,xK1}; 若Cx中的点xk,k∈{1,2,…,K1}有
则进入下一步, 否则验证下一个候选局部鞍点.
(b) 给定初始点y0, 求解如下问题:
(5)
得最优解集为Cy={y1,y2,…,yL1}; 若Cy中的点yl,l∈{1,2,…,L1}有
(c) 当C2中所有的候选局部鞍点验证完毕, 若S为空集, 则目标函数在X×Y上不存在局部鞍点, 算法终止.
该算法可以计算出f(x,y)在X×Y上的局部鞍点(x*,y*), 以及对应的局部鞍点值f*.在X×Y上, 函数f(x,y)的局部鞍点与全局鞍点有如下的关系.
定理1.1假设f(x,y)是X×Y上的二阶连续可微函数, 若(x*,y*)是f(x,y)在X×Y上的全局鞍点, 则(x*,y*)为X×Y上的局部鞍点.
证明若(x*,y*)是f(x,y)在X×Y上的全局鞍点, 由定义1.1可知, 下列不等式成立:
f(x*,y)≤f(x*,y*)≤f(x,y*), ∀x∈X,∀y∈Y.
假设(x*,y*)不是局部鞍点, 则至少存在一点(x,y)∈[X∩B(x*,γ)]×[Y∩B(y*,γ)], 使得不等式
f(x*,y)≤f(x*,y*)≤f(x,y*)
(6)
不成立.又
[X∩B(x*,γ)]⊆X, [Y∩B(y*,γ)]⊆Y,
因此不等式(6)不成立的结论与定义1.1矛盾.从而(x*,y*)为f(x,y)在X×Y上的局部鞍点.
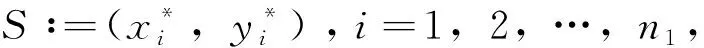
即验证局部鞍点是否是全局鞍点.
算法2


(a)求解如下问题:
(7)
鞍点, 算法终止.
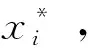
(a)求解如下问题
(8)
注: 在算法1和2中, 计算优化子问题时, 本文均利用MATLAB中的求解器MultiStart(Global Optimization Toolbox)求解[17].Multistart在求解优化子问题时, 根据给定的点(x0,y0),先通过在区域内生成一系列初始点, 再运用内点法, SQP等方法来求解相应的优化问题.因此, 若生成的初始点在区域内分布均匀, 并且足够多时, 算法1步1的所有候选局部鞍点, 步2中的所有局部最小点和局部最大点, 以及算法2中的所有全局最小点和全局最大点都是可以得到的.
2 收敛性分析
设x∈Rd, 无约束优化问题
ming(x)
(9)
具有以下一阶、二阶最优性条件[18].
定理2.1(一阶必要条件) 设g(x)在开集D上一阶连续可微.若x*∈D是问题(5)的一个局部极小点, 则必有∇g(x*)=0.
定理2.2(二阶必要条件) 设g(x)在开集D上二阶连续可微.若x*∈D是问题(5)的一个局部极小点, 则必有∇g(x*)=0且∇2g(x*)是半正定矩阵.
下面给出(x*,y*)是f(x,y)的局部鞍点的必要条件.
定理2.3假设f(x,y)是Rn×Rm上的二阶连续可微函数, 若(x*,y*)是f(x,y)在Rn×Rm上的局部鞍点, 则
(10)
证明若(x*,y*)是f(x,y)在Rn×Rm上的局部鞍点, 则由定义1.2可得:
f(x*,y*)≤f(x,y*), ∀x∈B(x*,γ),
又由局部极小点的定义可知,x*为f(x,y*)的局部极小点.
根据定理2.1和定理2.2可得:
同理, 根据
f(x*,y)≤f(x*,y*) ∀y∈B(y*,γ),
可以得到
由定理2.3可知, 若f(x,y)在X×Y上存在局部鞍点, 则通过算法1中步1, 得到满足条件(10)的全部候选鞍点的集合C2, 且局部鞍点(x*,y*)∈C2.

证明因为f(x,y)∈C2(X×Y)在X×Y上的局部鞍点只有有限个, 算法1的初始点在X×Y上分布均匀, 并且足够多, 领域半径γ很小.则算法1中所有的候选局部鞍点的集合C2, 步2中所有的局部最小点的集合Cx与所有的局部最大点的集合Cy都是可以得到的.
f(x*,y*)≤f(x,y*),∀x∈X∩B(x*,γ),
f(x*,y)≤f(x*,y*),∀y∈Y∩B(y*,γ),
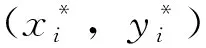


(11)
3 数值实验
本节通过数值实验来验证算法1和2的有效性.所有的数值结果均在华硕电脑上通过MATLAB 2016b计算得到.电脑配置如下: 双核 3.10 GHz CPU, 运行内存为 4GB.MATLAB 通过调用MultiStart来计算候选局部鞍点集合[17], 以及求解算法1和算法2中的最小、最大化子问题.
下列所有数值实验中, (x0,y0)表示初始点,k表示第k个局部鞍点, (x*,y*)表示局部鞍点的坐标,f*表示对应的局部鞍点值.在以下算例的计算中, 取γ=0.01.
算例1目标函数
给定区域(x,y)∈[-1,1]×[-1,1].利用算法1, 取初始点(x0,y0)=(0,0), 得到候选局部鞍点为(x1,y1)=(0.124 3,-0.456 4),(x2,y2)=(-0.456 5,0.573 3), 通过算法1的步2验证出这两个点均不是局部鞍点. 计算时间t=6.112 s.
给定区域(x,y)∈[-10,10]×[-10,10], 取初始点(x0,y0)=(0,0), 得到16个候选局部鞍点, 通过算法1的步2验证这16个点均不是局部鞍点.
算例2目标函数
给定区域(x,y)∈[-10,10]3×[-10,10]3.利用算法1, 取初始点(x0,y0)=(1,1,1,1,1,1), 候选局部鞍点集合为空, 即在区域[-10,10]3×[-10,10]3上不存在局部鞍点.计算时间t=8.429 s.
算例3目标函数
给定区域(x,y)∈[-10,10]3×[-10,10]3.利用算法1, 取初始点(x0,y0)=(0,0,0,0,0,0), 得到候选局部鞍点(0,0,0,0,0,0), 通过算法1验证后可知此点是唯一的局部鞍点, 局部鞍点值f*=0, 计算时间t1=72.751 s.
取初始点(x0,y0)=(1,1,1,1,1,1), 得到相同局部鞍点(0,0,0,0,0,0), 计算时间t2=74.185 s.又由算法2可验证出此局部鞍点不是[-10,10]3×[-10,10]3上的全局鞍点.
算例4目标函数
f(x,y)=e-y2-(x+1)2-e-x2+(y+1)2+ex2-y2.
给定区域(x,y)∈[-10,10]×[-10,10].利用算法1, 取初始点(x0,y0)=(1,1), 算得到候选局部鞍点(0.120 5,-0.557 3), 通过算法1验证后可知此点是唯一的局部鞍点, 局鞍点值f*=-0.246 4.计算时间t1=12.680 s.
取初始点(x0,y0)=(5,5), 得到相同的局部鞍点(0.120 5,-0.557 3), 计算时间t2=9.931 s.又由算法2可验证出此局部鞍点是[-10,10]×[-10,10]上的全局鞍点.
算例5目标函数
给定区域(x,y)∈[-5,5]3×[-5,5]3.利用算法1, 取初始点(x0,y0)=(0,0,0,0,0,0),计算得到候选局部鞍点(-0.716 7,-0.716 7,-0.716 7,0.586 6,0.586 6,0.586 6).通过算法1验证后可知此点是唯一的局部鞍点.局部鞍点值f*=1.320 8.计算时间t1=37.518 s
取初始点(x0,y0)=(1,0.5,1,1.5,2,1), 得到相同的局部鞍点, 计算时间t2=37.450 s.又由算法2可验证出此局部鞍点不是[-5,5]3×[-5,5]3上的全局鞍点.
算例6目标函数
f(x,y)=x4y2-x2y4+x3y-xy3+x-y.
给定区域(x,y)∈[-2,2]×[-2,2].利用算法1, 分别取初始点(x0,y0)=(0,0)与(x0,y0)=(-0.5,1.5), 计算得到的局部鞍点相同,计算时间为t1=15.081 s和t2=15.061 s.结果见表1.

表1 算例6的数值结果
从表1可以看出给定区域上有3个局部鞍点.由算法2可验证局部鞍点(-0.695 8,-0.695 8)是[-2,2]×[-2,2]上的全局鞍点.
算例7目标函数
f(x,y)=xcosy+ysinx.
给定区域(x,y)∈[-8,8]×[-8,8].利用算法1,分别取初始点(x0,y0)=(0,0)与(x0,y0)=(-2.5,2.5),计算得到的局部鞍点相同,计算时间为t1=15.192 s和t2=14.509s.结果见表2.

表2 算例7的数值结果
从表2可以看出在给定区域上有6个局部鞍点.由算法2可验证这6个点均不是[-8,8]×[-8,8]上的全局鞍点.
算例8目标函数
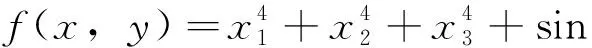
给定区域(x,y)∈[-5,5]3×[-5,5]3.利用算法1, 分别取初始点(x0,y0)=(0,0,0,0,0,0)与(x0,y0)=(1,1,1,1,1,1), 计算得到的局部鞍点相同, 计算时间分别为t1=73.059 s和t1=70.782 s.结果见表3.

表3 算例8的数值结果
从表3可以看出在给定区域上存在8个局部鞍点.由算法2可验证点(-0.592 0,-0.592 0,-0.592 0,±0.490 0,±0.490 0,±0.490 0)均为[-5,5]3×[-5,5]3上的全局鞍点.
上述算例在计算中, 初始点选取在给定的区域内即可.通过以上算例可知, 候选局部鞍点不一定为局部鞍点, 局部鞍点存在时, 全局鞍点不一定存在.由算例8可知, 如果区域上的全局鞍点存在, 全局鞍点可能不是唯一的.
以上算例的数值结果表明, 本文提出的无约束局部鞍点问题的数值算法和验证局部鞍点是否是全局鞍点的算法是可行的.
4 总结
本文研究了无约束函数局部鞍点的计算问题,当变量x和y限定于一些一般约束时, 本文提出的方法不再有效.因此, 如何针对带有一般约束条件的局部鞍点问题, 提出有效的数值算法是一个值得进一步研究的问题.

