改进的复制动态方程及其稳定性分析

吴克晴，冯兴来

（江西理工大学理学院，江西 赣州　341000）

改进的复制动态方程及其稳定性分析

吴克晴，冯兴来

（江西理工大学理学院，江西 赣州341000）

针对原复制动态建立过程的缺陷，通过引入强度系数，使博弈参与者采取不同策略时更显得相互依赖，体现出不同策略被采用的变化情况，扩展了进化博弈论的框架.针对均有两个策略的两个博弈参与者，研究分析了扩展后复制动态的稳定性，对以后科学管理具有重要指导意义.

进化博弈；复制动态；强度系数；进化稳定策略

1　引言

进化博弈理论的思想起源于达尔文的生物进化理论和拉马克的遗传基因理论［1］，视博弈参与者为有限理性，以群体为研究对象，其两个基本的概念是进化稳定策略［2］和复制动态方程［3］，前者强调的是变异，后者强调的是选择，由于变异后仍需要选择，所以建立策略随时间的总体动态非常关键，然而在运用进化博弈理论时，专家学者广泛采用文献［3］中的复制动态方程：其思想是选择某一特定策略频率的变化就等于该策略的适应度与群体平均适应度之间的差值，这种做法虽然克服了学习能力弱的个体在无法用“最优反应动态”模拟策略［4］选择时的困惑，然而并未考虑同一群体下策略间的相互依赖情况.

2　复制动态的构造

对于一群体A，假设存在n1种状态，且在t时刻第i（i=1，2，···，n1）种状态下小群体的数量为mi（t），生存适应能力为ui（t），所占群体A的比率为xi（t），t时刻群体A的平均生存适应度为

3　复制动态的进化分析

多个群体的复制动态的进化稳定性分析，可以从对两个群体两种选择状态的稳定性分析开始.本节就两种选择状态的两个群体展开其稳定性分析.

假设有两个博弈参与者A和B，均存在两种选择状态，其收益矩阵如表1.

表1两个博弈参与者A和B的收益矩阵

上表中a，b，c，d，e，f，g，h表示各博弈状态下的值；x1（t）与x2（t）分别表示t时刻A在第一、第二种状态下的数量所占A的比例；y1（t）与y2（t）分别为t时刻B在第一、第二种状态下的数量所占B的比例；λ1与λ2分别表示A在第一、第二种状态下的数量的自然增长率；ρ1与ρ2分别表示B在第一、第二种状态下的数量的自然增长率.

假设u1（t）与u2（t）分别表示t时刻A在第一、第二种状态下的收益；¯u为t时刻A的平均收益；w1（t）与w2（t）分别表示t时刻B在第一、第二种状态下的收益；¯w为t时刻B的平均收益，则

系统（5）的平衡点［6］的稳定性可通过文献［7］中提供的方法判别，即当系统（5）的雅可比矩阵的行列式为正值，其迹为负值时，平衡点是稳定的；行列式为正值，迹为正值时，平衡点是不稳定的；当行列式为负值时，迹为任意值时，平衡点为鞍点.由于参数值的大小未定，所以trJ 与detJ的符号未定，从而影响平衡点的稳定性，此分析过程略，现将所有的分析结果列举如下：

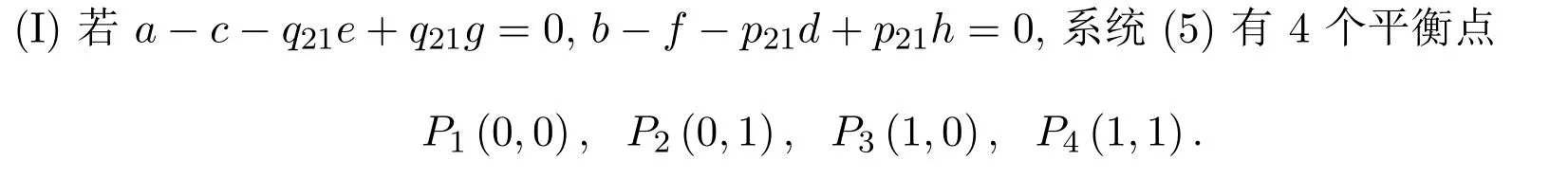
此时所有的分析结果为：

（1）当a-q21e＜0，f-p21h＜0时，P1（0，0）为稳定点，P2（0，1）、P3（1，0）为鞍点，P4（1，1）为不稳定点；

（2）当a-q21e＜0，f-p21h＞0时，P1（0，0）、P4（1，1）为鞍点，P2（0，1）为稳定点，P3（1，0）为不稳定点；

（3）当 a-q21e＞0，f-p21h＜0时，P1（0，0）、P4（1，1）为鞍点，P2（0，1）为不稳定点，P3（1，0）为稳定点；

（4）当 a-q21e＞0，f-p21h＞0时，P1（0，0）为不稳定点，P2（0，1）、P3（1，0）为鞍点，P4（1，1）为稳定点.

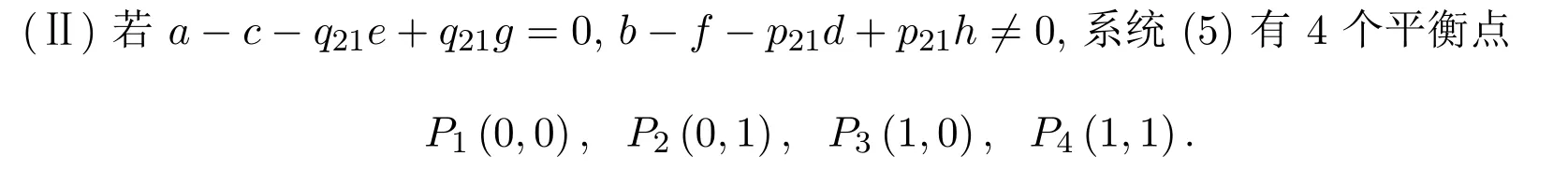
此时所有的分析结果为：

（1）当a-q21e＜0，b-p21d＜0，f-p21h＜0时，P1（0，0）为稳定点，P2（0，1）、P3（1，0）为鞍点，P4（1，1）为不稳定点；

（2）当a-q21e＜0，b-p21d＞0，f-p21h＜0时，P1（0，0）为稳定点，P2（0，1）、P4（1，1）为鞍点，P3（1，0）为不稳定点；

（3）当a-q21e＜0，b-p21d＜0，f-p21h＞0时，P1（0，0）、P3（1，0）为鞍点，P2（0，1）为稳定点，P4（1，1）为不稳定点；

（4）当a-q21e＜0，b-p21d＞0，f-p21h＞0时，P1（0，0）、P4（1，1）为鞍点，P2（0，1）为稳定点，P3（1，0）为不稳定点；

（5）当a-q21e＞0，b-p21d＜0，f-p21h＞0时，P1（0，0）为不稳定点，P2（0，1）、P4（1，1）为鞍点，P3（1，0）为稳定点；

（6）当a-q21e＞0，b-p21d＜0，f-p21h＜0时，P1（0，0）、P4（1，1）为鞍点，P2（0，1）为不稳定点，P3（1，0）为稳定点；

（7）当a-q21e＞0，b-p21d＞0，f-p21h＞0时，P1（0，0）为不稳定点，P2（0，1）、P3（1，0）为鞍点，P4（1，1）为稳定点；

（8）当a-q21e＞0，b-p21d＞0，f-p21h＜0时，P1（0，0）、P3（1，0）为鞍点，P2（0，1）为不稳定点，P4（1，1）为稳定点.

此时所有的分析结果为：

（1）当a-q21e＞0，c-q21g＜0，f-p21h＜0时，P1（0，0）为稳定点，P2（0，1）为不稳定点，P3（1，0）、P4（1，1）为鞍点；

（2）当a-q21e＜0，c-q21g＜0，f-p21h＜0时，P1（0，0）为稳定点，P2（0，1）、P3（1，0）为鞍点，P4（1，1）为不稳定点；

（3）当a-q21e＜0，c-q21g＞0，f-p21h＞0时，P1（0，0）为不稳定点，P3（1，0）、P4（1，1）为鞍点，P2（0，1）为稳定点；

（4）当a-q21e＜0，c-q21g＜0，f-p21h＞0时，P1（0，0）、P4（1，1）为鞍点，P2（0，1）为稳定点，P3（1，0）为不稳定点；

（5）当a-q21e＞0，c-q21g＞0，f-p21h＜0时，P1（0，0）、P4（1，1）为鞍点，P2（0，1）为不稳定点，P3（1，0）为稳定点；

（6）当a-q21e＜0，c-q21g＞0，f-p21h＜0时，P1（0，0）、P2（0，1）为鞍点，P3（1，0）为稳定点，P4（1，1）为不稳定点；

（7）当a-q21e＞0，c-q21g＞0，f-p21h＞0时，P1（0，0）为不稳定点，P2（0，1）、P3（1，0）为鞍点，P4（1，1）为稳定点；

（8）当a-q21e＞0，c-q21g＜0，f-p21h＞0时，P1（0，0）、P2（0，1）为鞍点，P3（1，0）为不稳定点，P4（1，1）为稳定点.

此时，需分以下几种情形进行讨论.

（1）当 a-q21e＜ c-q21g＜ 0，b-p21d＜ f-p21h＜ 0时，P1（0，0）为稳定点，P2（0，1）、P3（1，0）、P5（x∗，y∗）为鞍点，P4（1，1）为不稳定点；

（2）当 0＜c-q21g＜a-q21e，0＜f-p21h＜b-p21d时，P1（0，0）为不稳定点，P2（0，1）、P3（1，0）、P5（x∗，y∗）为鞍点，P4（1，1）为稳定点；

（3）当 0＜c-q21g＜a-q21e，b-p21d＜f-p21h＜0时，P1（0，0）、P4（1，1）为鞍点、P2（0，1）为不稳定点，P3（1，0）为稳定点，P5（x∗，y∗）为中心点；

（4）当a-q21e＜c-q21g＜0，0＜f-p21h＜b-p21d时，P1（0，0）、P4（1，1）为鞍点，P2（0，1）为稳定点，P3（1，0）为不稳定点，P5（x∗，y∗）为中心点.

（1）当 0＜c-q21g＜a-q21e，b-p21d＜0＜f-p21h时，P1（0，0）为不稳定点，P2（0，1）、P4（1，1）、P5（x∗，y∗）为鞍点，P3（1，0）为稳定点；

（2）当 a-q21e＜ c-q21g＜ 0，f-p21h＜ 0＜ b-p21d时，P1（0，0）为稳定点，P2（0，1）、P4（1，1）、P5（x∗，y∗）为鞍点，P3（1，0）为不稳定点；

（3）当a-q21e＜c-q21g＜0，b-p21d＜0＜f-p21h时，P1（0，0）、P3（1，0）为鞍点，P2（0，1）为稳定点，P4（1，1）为不稳定点，P5（x∗，y∗）为中心点；

（4）当0＜c-q21g＜a-q21e，f-p21h＜0＜b-p21d时，P1（0，0）、P3（1，0）为鞍点，P2（0，1）为不稳定点，P4（1，1）为稳定点，P5（x∗，y∗）为中心点.

（1）当 0＜c-q21g＜a-q21e，0＜b-p21d＜f-p21h时，P1（0，0）为不稳定点，P2（0，1）、P3（1，0）为鞍点，P4（1，1）为稳定点，P5（x∗，y∗）为中心点；

（2）当a-q21e＜c-q21g＜0，0＜b-p21d＜f-p21h时，P1（0，0）、P4（1，1）、P5（x∗，y∗）为鞍点，P2（0，1）为稳定点，P3（1，0）为不稳定点；

（3）当0＜c-q21g＜a-q21e，f-p21h＜b-p21d＜0时，P1（0，0）、P4（1，1）、P5（x∗，y∗）为鞍点，P2（0，1）为不稳定点，P3（1，0）为稳定点；

（4）当 a-q21e＜ c-q21g＜ 0，f-p21h＜ b-p21d＜ 0时，P1（0，0）为稳定点，P2（0，1）、P3（1，0）为鞍点，P4（1，1）为不稳定点，P5（x∗，y∗）为中心点.

（1）当a-q21e＜0＜c-q21g，0＜f-p21h＜b-p21d时，P1（0，0）为不稳定点，P2（0，1）为稳定点，P3（1，0）、P4（1，1）、P5（x∗，y∗）为鞍点；

（2）当c-q21g＜0＜a-q21e，0＜f-p21h＜b-p21d时，P1（0，0）、P2（0，1）为鞍点，P3（1，0）为不稳定点，P4（1，1）为稳定点，P5（x∗，y∗）为中心点；

（3）当c-q21g＜0＜a-q21e，b-p21d＜f-p21h＜0时，P1（0，0）为稳定点，P2（0，1）为不稳定点，P3（1，0）、P4（1，1）、P5（x∗，y∗）为鞍点；

（4）当a-q21e＜0＜c-q21g，b-p21d＜f-p21h＜0时，P1（0，0）、P2（0，1）为鞍点，P3（1，0）为稳定点，P4（1，1）为不稳定点，P5（x∗，y∗）为中心点.

（1）当a-q21e＜0＜c-q21g，f-p21h＜0＜b-p21d时，P1（0，0）、P4（1，1）为不稳定点，P2（0，1）、P3（1，0）为稳定点，P5（x∗，y∗）为鞍点；

（2）当c-q21g＜0＜a-q21e，b-p21d＜0＜f-p21h时，P1（0，0）、P4（1，1）为稳定点，P2（0，1）、P3（1，0）为不稳定点，P5（x∗，y∗）为鞍点；

（3）当c-q21g＜0＜a-q21e，f-p21h＜0＜b-p21d时，P1（0，0）、P2（0，1）、P3（1，0），P4（1，1）为鞍点，P5（x∗，y∗）为中心点；

（4）当a-q21e＜0＜c-q21g，b-p21d＜0＜f-p21h时，P1（0，0）、P2（0，1）、P3（1，0），P4（1，1）为鞍点，P5（x∗，y∗）为中心点.

（1）当a-q21e＜0＜c-q21g，0＜b-p21d＜f-p21h时，P1（0，0）为不稳定点，P2（0，1）为稳定点，P3（1，0）、P4（1，1）为鞍点，P5（x∗，y∗）为中心点；

（2）当c-q21g＜0＜a-q21e，f-p21h＜b-p21d＜0时，P1（0，0）为稳定点，P2（0，1）为不稳定点，P3（1，0）、P4（1，1）为鞍点，P5（x∗，y∗）为中心点；

（3）当c-q21g＜0＜a-q21e，0＜b-p21d＜f-p21h时，P1（0，0）、P2（0，1）、P5（x∗，y∗）为鞍点，P3（1，0）为不稳定点，P4（1，1）为稳定点；

（4）当a-q21e＜0＜c-q21g，f-p21h＜b-p21d＜0时，P1（0，0）、P2（0，1）、P5（x∗，y∗）为鞍点，P3（1，0）为稳定点，P4（1，1）为不稳定点.

（1）当 0＜a-q21e＜c-q21g，0＜f-p21h＜b-p21d时，P1（0，0）为不稳定点，P2（0，1）、P3（1，0）为鞍点，P4（1，1）为稳定点，P5（x∗，y∗）为中心点；

（2）当 c-q21g＜ a-q21e＜ 0，b-p21d＜ f-p21h＜ 0时，P1（0，0）为稳定点，P2（0，1）、P3（1，0）为鞍点，P4（1，1）为不稳定点，P5（x∗，y∗）为中心点；

（3）当c-q21g＜a-q21e＜0，0＜f-p21h＜b-p21d时，P1（0，0）、P4（1，1）、P5（x∗，y∗）为鞍点，P2（0，1）为稳定点，P3（1，0）为不稳定点；

（4）当0＜a-q21e＜c-q21g，b-p21d＜f-p21h＜0时，P1（0，0）、P4（1，1）、P5（x∗，y∗）为鞍点，P2（0，1）为不稳定点，P3（1，0）为稳定点.

（1）当 0＜a-q21e＜c-q21g，b-p21d＜0＜f-p21h时，P1（0，0）为不稳定点，P2（0，1）、P4（1，1）为鞍点，P3（1，0）为稳定点，P5（x∗，y∗）为中心点；

（2）当 c-q21g＜ a-q21e＜ 0，f-p21h＜ 0＜ b-p21d时，P1（0，0）为稳定点，P2（0，1）、P4（1，1）为鞍点，P3（1，0）为不稳定点，P5（x∗，y∗）为中心点；

（3）当c-q21g＜a-q21e＜0，b-p21d＜0＜f-p21h时，P1（0，0）、P3（1，0）、P5（x∗，y∗）为鞍点，P2（0，1）为稳定点，P4（1，1）为不稳定点；

（4）当0＜a-q21e＜c-q21g，f-p21h＜0＜b-p21d时，P1（0，0）、P3（1，0）、P5（x∗，y∗）为鞍点，P2（0，1）为不稳定点，P4（1，1）为稳定点；

（1）当 0＜a-q21e＜c-q21g，0＜b-p21d＜f-p21h时，P1（0，0）为不稳定点，P2（0，1）、P3（1，0），P5（x∗，y∗）为鞍点，P4（1，1）为稳定点；

（2）当 c-q21g＜ a-q21e＜ 0，f-p21h＜ b-p21d＜ 0时，P1（0，0）为稳定点，P2（0，1）、P3（1，0），P5（x∗，y∗）为鞍点，P4（1，1）为不稳定点；

（3）当c-q21g＜a-q21e＜0，0＜b-p21d＜f-p21h时，P1（0，0）、P4（1，1）为鞍点，P2（0，1）为稳定点，P3（1，0）为不稳定点，P5（x∗，y∗）为中心点.

（4）当0＜a-q21e＜c-q21g，f-p21h＜b-p21d＜0时，P1（0，0）、P4（1，1）为鞍点，P2（0，1）为不稳定点，P3（1，0）为稳定点，P5（x∗，y∗）为中心点.

4　进一步分析

根据以上分析，当收益矩阵中参数值满足（I）或（II）或（III）的时，系统（5）有4个平衡点

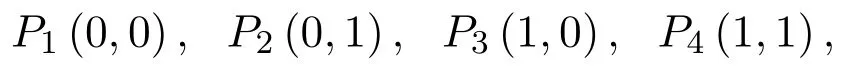
随着时间推移，最终的稳态平衡点唯一，且该平衡点的进化与强度系数λi，ρi（i=1，2）有关；但当收益矩阵中参数值满足（Ⅳ）时，系统（5）有5个平衡点

经过时间进化最终可能没有稳态平衡点或稳态平衡点不一定唯一（如（Ⅳ）下的情形5），而对于两个稳态平衡点中偏向哪一个的程度或处于中心点偏向哪一个状态的程度也与强度系数λi，ρi（i=1，2）有关，下面不妨以（Ⅳ）下情形5中（1）的情况进行分析，其它情况可类似.

（Ⅳ）情形5中（1）的情况：当

时，P1（0，0），P4（1，1）为不稳定点，P2（0，1），P3（1，0）为稳定点，P5（x∗，y∗）为鞍点.此时，系统的动态演化图［8-9］如图1所示.

在此情况下，显然P5（x∗，y∗）为以P1（0，0），P3（1，0），P4（1，1），P2（0，1）为顶点组成的四边形中的一个内部点.

根据几何图形及相关知识，由P1（0，0），P3（1，0），P4（1，1），P5（x∗，y∗）为顶点围成的四边形区域面积S为：

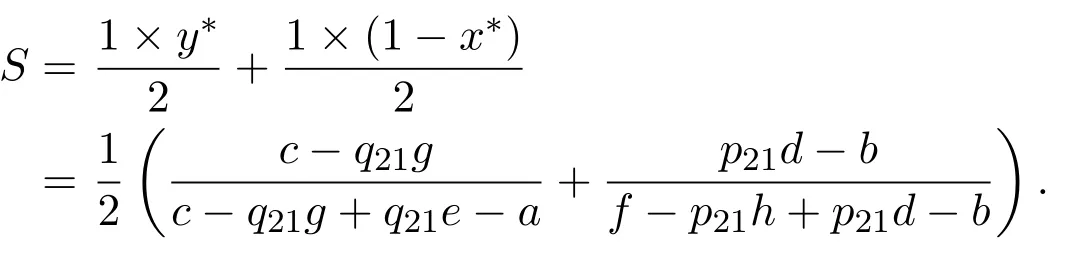
由于

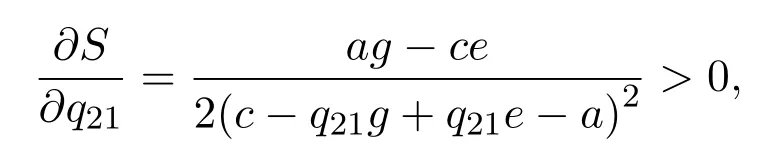
所以当增加q21时，S会增大，即当博弈参与者A在两种状态下增长率λ2与λ1的比值q21越大，其均衡策略为x1（t）=1.

同理，由于

所以当增加p21时，S会减少，即当博弈参与者B两种状态下增长率ρ2与ρ1的比值p21越大，其均衡策略为y1（t）=0，从而系统（5）的稳定状态更趋于平衡点P3（1，0），反之，系统（5）的稳定状态更趋于平衡点P2（0，1）.

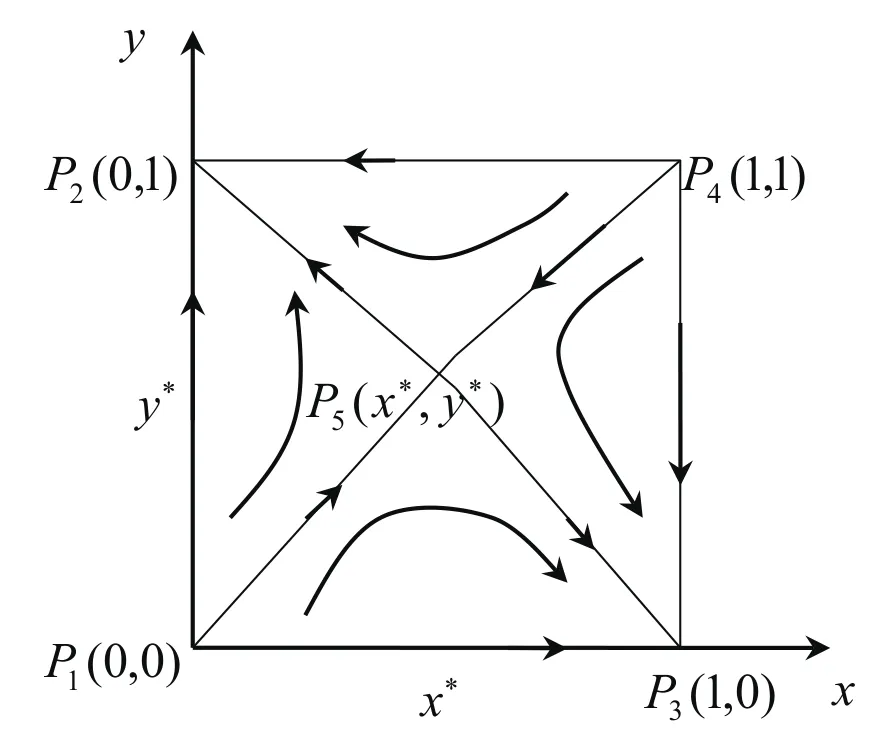
图1当a-q21e＜0＜c-q21g，f-p21h＜0＜b-p21d时的动态演化图

5　结语

本文通过引入强度系数，扩展了文献［3］中的进化博弈论框架.并针对两个策略的两个博弈参与者的情形，分析了他们采取不同策略时的进化稳定性情况，反映出强度系数对博弈决策的影响；最后，进一步研究表明了强度系数影响参与者在多个稳态下最终的优化行为，即影响动态系统稳定状态的演变趋势.

可以看到，虽然本文局限于分析两个策略的两个博弈参与者的情形，但对于多个博弈参与者多种策略的稳定状态，类似可得到研究.即方程（5）解的稳定状态分析对方程（3）解的稳定状态分析具有基础作用，仅计算量相对较为复杂.这对以后利用进化博弈理论，来解决分析实际问题具有重要的指导作用.

［1］殷辉，陈劲，谢芳.开放式创新下产学合作的演化博弈分析［J］.情报杂志，2012，31（9）：185-190.

［2］Smith J M.Evolution and the Theory of Games［M］.New York：Cambridge University Press，1982.

［3］Taylor P D，Jonker L B.Evolutionary stable strategies and game dynamics［J］.Mathematical Bioscience，1978，40：145-156.

［4］刘伟兵，王先甲.进化博弈决策机制设计综述［M］.运筹与管理，2008，17（1）：84-87.

［5］赵琼，别群益.一类修正的 Holling-Tanner捕食模型的持久性和全局渐近稳定性 ［J］.数学的实践与认识，2013，43（18）：292-298.

［6］何德明，何万生，谢保利.一类具有线性收获率的生物捕食系统的定性分析 ［J］.纯粹数学与应用数学，2013，29（1）：33-39.

［7］郭军华，李帮义，倪明.双寡头再制造进入决策的演化博弈分析［J］.系统工程理论与实践，2013，33（2）：330-377.

［8］王磊，张庆普.基于惯例视角的高校科研团队创造力演化博弈分析［J］.科学学与科学技术管理，2012，33（8）：82-90.

［9］梅强，马国建，杜建国，等.中小企业安全生产管制路径演化研究［J］.中国管理科学，2009，17（2）：160-168.

Improved replicated dynamic equations and its stability analysis

Wu Keqing，Feng Xinglai

（College of Science，Jiangxi University of Science and Technology，Ganzhou341000，China）

Based on the defects from the original replicated dynamic establishment，different strategies adopted are made more interdependent for game players by introducing strength coefficient，the changes of different strategies adopted are better reflected，and the framework of evolutionary game theory is extended.For two game players with two strategies，the stability of the replicated dynamics improved is analyzed.As a result，the analysis obtained in this paper has important guiding significance for scientific management.

evolutionary game，replicated dynamic，strength coefficient，evolutionarily stable strategy

O225；F224.32

A

1008-5513（2015）03-0221-10

10.3969/j.issn.1008-5513.2015.03.001

2014-02-20.

国家自然科学基金（61364015，61064006）.

吴克晴（1972-），博士，副教授，研究方向：运筹学、泛函分析.

2010 MSC：91A22，93C15