AANA序列的半参数模型的强相合性

张鸽，胡宏昌，张宇

（湖北师范学院数学与统计学院，湖北 黄石　435000）

AANA序列的半参数模型的强相合性

张鸽，胡宏昌，张宇

（湖北师范学院数学与统计学院，湖北 黄石435000）

讨论渐近几乎负相依序列的半参数模型，利用最小二乘法和非参数加权的估计方法，得到参数、非参数和误差方差的估计，并在合适的条件下得到这些估计量的强相合性，推广了负相依序列的半参数模型的相应结论.

半参数模型；渐近几乎负相依；强相合性

1　引言

讨论如下半参数模型：

其中 （xi，ti）为随机设计点列，β为待估的未知参数，g（·）是定义在闭区间 ［0，1］上未知的可测函数，随机误差序列 ｛εi｝为渐近几乎负相依序列 （简记为 AANA，定义见定义 1.1），且

假设存在定义在［0，1］上的某一函数h（·），有［1］

其中｛ηi｝是独立同分布序列，Eηi=0，且｛ηi｝与｛εi｝相互独立.

定义 1.1［2］称随机变量序列 ｛Xn，n≥1｝是 AANA序列，如果存在非负实数序列对所有n，k≥1满足：

其中f和g是对所有方差存在且对每个变元均非降连续的函数.

NA序列［2］在八十年代被引入，由于其在可靠性理论、渗透理论及多元统计分析中的广泛应用而备受关注，对于误差为NA序列的半参数回归模型，目前已经得到了许多重要的结果.例如：文献［3］研究了NA样本半参数回归模型的矩相合性；文献［4］研究了NA序列下半参数模型中小波估计的收敛速度；文献［5］研究了NA样本下半参数模型的渐近性质；文献［6］研究了误差为NA的半参数模型的弱相合性等.由此可见对于NA序列的半参数模型的研究具有一定的意义.AANA序列是一类广泛的负相依序列，对其研究具有一定的价值.目前，已经有大量的文献研究AANA序列，如文献［7］研究了Marcinkiewicz和Zygmund因变量的强大数定律的扩展；文献［8］研究了渐近几乎负相依随机变量的Rosenthal型不等式及其应用.若随机变量序列是NA序列，则它们一定是AANA序列，反之不真［7］.因此，AANA误差的半参数回归模型是NA误差的半参数回归模型的一个自然推广，从而研究前者将具有重要的意义.目前误差为AANA序列的半参数回归模型的研究还没有开始，因此本文初步研究模型（1）和模型（2）.

2　估计方法及主要结果

注2.1相对于独立随机误差而言，结论中的矩条件要减弱.但要减弱以上结论中关于｛εi｝的矩条件，则需要减弱下文引理3.2和引理3.3中的矩条件.然而减弱引理3.2和引理3.3中的矩条件也许是一件非常困难的事，因此实质性地减弱以上结果的条件并非易事.若｛εi｝为NA序列，则以上结论仍成立，由此可知，这些结论推广了NA序列的半参数模型的相应结论.另外，上述结论很容易推广到多维的情形.

3　主要结果的证明

为了证明的需要，先给出如下引理：

引理3.1［9］随机变量｛Xn，n≥1｝是AANA序列，其混合系数为｛q（n），n≥1｝，｛fi，i≥1｝是非增（或非减）的函数，则｛fn（Xn），n≥1｝仍是混合系数为｛q（n），n≥1｝的AANA序列.

引理 3.2假定｛εi；1≤i≤n｝是混合系数为｛q（n），n≥1｝的AANA序列，且满足

引理 3.3假定｛εi；1≤i≤n｝是混合系数为｛q（n），n≥1｝的AANA序列，且满足

又设定义在闭区间［0，1］上的实函数序列｛ani（·），1≤i≤n，n≥1｝满足：

引理3.4当条件A1和A2满足时，有

引理 3.5［10］设｛ηi；1≤i≤n｝是相互独立的随机变量，又设Wnj（t）是定义在［0，1］的权函数，且满足下述条件：

定理2.1的证明由（3）式和模型（1），可得

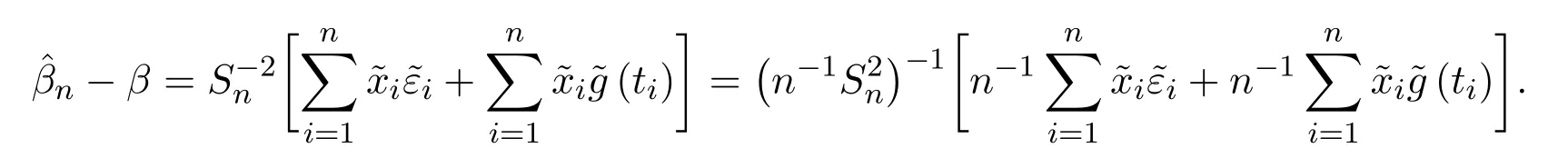
定理2.2的证明由（4）式和模型（1）可得

定理2.3的证明由（5）式和模型（1）可得

［1］Speckman P.Kernel smoothing in partial linear models［J］.J.Roy.Statist.Soc.B.，1988，50：413-436.

［2］Kim Tae sung，Ko Mi hwa，Lee Il hyun.On the strong law for asymptotically almost negatively associated random variables［J］.Rocky Mountain Journal of Mathematics，2004，34（3）：979-989.

［3］Zhou X C，Liu X S，Hu S H.Moment consistency of estimators in partially linear models under NA samples［J］.Metrika，2009，DOI：10.1007/s00184-009-0260-5.

［4］Hu H C，Wu L.Convergence rates of wavelet estimators in semiparametric regression models under NA samples［J］.Chinese Annals of Mathematics，Series B，2012，33（4）：609-624.

［5］Baek J，Liang H Y.Asymptotics of estimators in semi-parametric model under NA samples［J］.Journal of Statistical Planning and Inference，2006，136（10）：3362-3382.

［6］Zhang J，Hu H C，Zhu D D.Weak consistency of semi parametric random design regression model under NA samples［J］.Journal of mathematics，2013，33（5）：849-856.

［7］Chandra T K，Ghosal S.Extensions of the strong law of large numbers of Marcinkiewicz and Zygmund for dependent variables［J］.Acta Mathematica Hungarica，1996，71（4）：327-336.

［8］Yuan D M，An J.Rosenthal type inequalities for asymptotically almost negatively associated random variables and application［J］.Science in China Series A：Mathematics，2009，52（9）：1887-1904.

［9］Yuan Demei，An Jun.Rosental type inequalities for asymptotically almost negatively associated random variables and applications［J］.Science in China Series，2009，52（9）：1887-1904.

［10］Gao J T，Zhao L C.Adaptive estimation in partly linear regression models［J］.Science in China Series，1992，22（8）：791-803.

The strong consistency of semiparametric model with AANA errors

Zhang Ge，Hu Hongchang，Zhang Yu

（College of Mathematics and Statistics，Hubei Normal University，Huangshi435002，China）

We consider the semiparametric model with almost asymptotically negatively dependent errors.Using the least squares estimate and the weight function method，we obtain estimators of parameter，nonparameter and error variance，and discuss their strong consistency under some suitable conditions.We generalize the corresponding conclusion about semiparametric regression models with negatively associated random errors.

semiparametric model，asymptotically almost negatively associated，strong consistency

O212.2

A

1008-5513（2015）03-0296-11

10.3969/j.issn.1008-5513.2015.03.011

2014-12-01.

国家自然科学基金（11471105，11471223）.

张鸽（1990-），硕士生，研究方向：应用概率统计.

胡宏昌（1971-），博士，教授，研究方向：应用概率统计.

2010 MSC：65U05