Fourier分析中的几个核函数研究

王志珍

（上海师范大学数理学院，上海 200234）

Fourier分析中的几个核函数研究

王志珍

（上海师范大学数理学院，上海 200234）

研究Fourier分析中的Dirichlet核函数、Fejér核函数和Poisson核函数，介绍优核的概念.证明Dirichlet核函数不是优核，Fejér核函数和Poisson核函数是优核.

优核；Dirichlet核函数；Fejér核函数；Poisson核函数

1　引言

Fourier分析是分析领域的重要基础和组成部分，随着数学与科技的不断发展，Fourier分析也在越来越多的领域展示出其重要性.Fourier分析既可以应用于纯数学领域（如数论）［1］，又是应用数学领域（如信号与图像处理）的重要工具［2］.文献［3-4］通过构建基于Fourier分析的浓度动量法对湿地环境进行研究，得到湿地滩涂流的解析解，从而给出湿地环境弥散现象的细节描述.

给定一以2π为周期的可积函数f（x），其Fourier级数展开为：

一个自然的问题是：如果f（x）在某一点x处连续，其Fourier级数能否在这一点收敛到f（x）？更进一步，如果f（x）处处连续，其Fourier级数能否一致收敛到f（x）？实际上关于Fourier级数收敛性的研究很早就开始了，早在十九世纪，Dirichlet就给出了著名的Dirichlet收敛定理［5］，但其结果只是针对Fourier级数常规求和而言的.如果只考虑常规求和，一个连续函数的Fourier级数展开甚至可能不收敛.Zygmund曾构造出一个在区间［-π，π］连续的函数，但其Fourier级数在［-π，π］上可列个点处发散的例子［6］.之后人们注意到级数的求和方法可以不拘泥于常规求和，并引入Cesàro求和与Abel求和以丰富级数求和理论.文献［7］研究了这三种求和方式优缺点，指出常规求和适用范围最小，Abel求和适用范围最广.本文将通过改变Fourier级数的求和方式并引入相应的核函数概念，研究Fourier级数在不同求和方式下其收敛性会有哪些有趣的结果.

2　核函数概念

定义Dirichlet核函数如下：

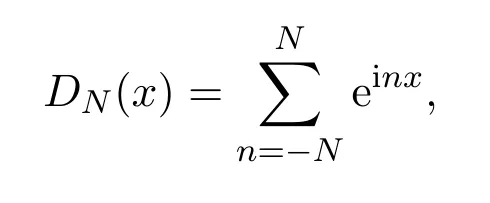
则f（x）的Fourier级数的部分和可写为：

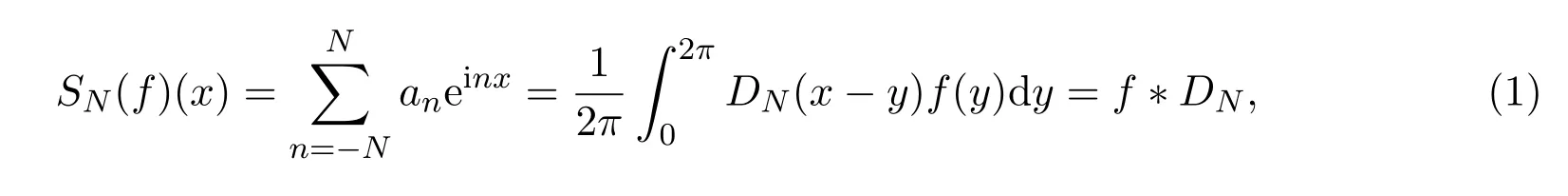
即f（x）的Fourier级数的部分和可视为f（x）与Dirichlet核函数作卷积.

定义2.1给定一族函数｛Kn（x）｝，如果满足如下三个条件：

注2.1文献［1］给出了关于优核的非常重要而有用的结论：如果｛Kn（x）｝是一族优核，则若f（x）在点x处连续，必有

若f（x）处处连续，则极限是一致收敛的.

接下来，以这个结论为出发点，考察f（x）的Fourier级数在不同求和方式下的收敛问题.

3　三类核函数研究

首先考察Dirchlet核函数，有如下结论.

定理 3.1Dirichlet核函数不是优核.

如果函数f（x）只满足连续性条件，那么其Fourier级数不能保证收敛到f（x），这与定理2.1的结论相符.那么如何去改进呢？文献［7］指出对级数采用不同的求和方式可能会使发散的级数变得收敛，Abel可和的适用范围要大于Cesàro可和，而Cesàro可和要比常规可和的适用范围更广.受这个结论启发，本文首先研究将Fourier级数由常规求和改为Cesàro求和会得到什么结论.由（1）式知Sn（f）=f∗Dn，现在对Fourier级数取N阶Cesàro平均，得

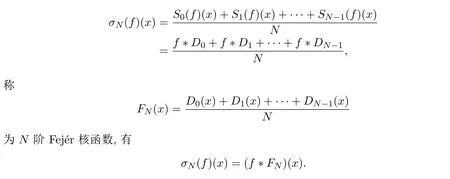
这样可将Fourier级数在Cesàro求和方式下的收敛性问题转化为研究函数f（x）与Fejér核函数做卷积的收敛性问题.关于Fejér核函数，有如下结论.

定理 3.2Fejér核函数是优核.

注3.1根据注2.1和定理3.1可知，若函数f（x）在点x处连续，则其Fourier级数的Cesàro和会在点x处收敛到f（x）；如果函数f（x）是处处连续的，则其Fourier级数的Cesàro和会一致收敛到f（x）.

最后研究将Fourier级数求和方式改为适用范围最广的Abel求和会有什么结果.

定理 3.3Poisson核函数是优核.

注3.2根据注2.1和定理3.3可得结论：若函数f（x）在点x处连续，则其Fourier级数的Abel和会在点x处收敛到f（x），如果函数f（x）是处处连续的，则其Fourier级数的Abel和会一致收敛到f（x）.

4　结论

函数f（x）的Fourier级数展开可视为f（x）与某个核函数作卷积，对Fourier级数采用不同的求和方式相当于让f（x）与不同的核函数作卷积.本文首先介绍了优核的概念并指出，一个优核可以让卷积运算具有好的收敛性.通过这一点可以指出：若对Fourier级数采用常规求和，即让f（x）与Dirichlet核函数做卷积，并不能保证级数一致收敛到连续函数f（x）；若对Fourier级数采用Cesàro求和或者Abel求和，即让f（x）与Fejér核函数或Poisson核函数作卷积，则可以保证级数一致收敛到连续函数f（x）.

［1］Stein E M，Shakarchi R.Fourier Analysis，an Introduction［M］.Princeton：Princeton Univ.Press，2011.

［2］Blackledge J M，Digital Image Processing.Mathematical and Computational Methods［M］.Chichester：Horwood Publishing，2005.

［3］Wu Z，Zeng L，Chen G Q，et al.Environmental dispersion in a tidal flow through a depth-dominated wetland［J］.Communications in Nonlinear Science and Numerical Simulation，2012，17：5007-5025.

［4］Zeng L，Chen G Q，Wu Z，et al.Flow distribution and environmental dispersivity in a tidal wetland channel of rectangular cross-section［J］.Communications in Nonlinear Science and Numerical Simulation，2012，17：4192-4209.

［5］Dirichlet G L.Sur la convergence des séries trigonomentriques qui serventà representer une fonction arbitraire entre des limites données［J］.Crelle，Journal für die reine angewandte Mathematik，1829，4：157-169.

［6］Zygmund A.Trigonomentical Series［M］.Cambridge：Cambridge Univ.Press，1959.

［7］张立柱.级数的常规可和，Cesàro可和与Abel可和的几点讨论［J］.纯粹数学与应用数学，2013，29（6）：565-571.

［8］陈纪修，於崇华，金路.数学分析［M］.2版.北京：高等教育出版社，2004.

Studies on several kernels in Fourier analysis

Wang Zhizhen
（Mathematics&Science College，Shanghai Normal University，Shanghai200233，China）

Dirichlet kernel，Fejér kernel and Poisson kernel in Fourier analysis are studied in this paper，the concept of good kernel is introduced and we proved that Dirichlet kernel is not a good kernel but Fejér kernel and Poisson kernel are good kernels.

good kernel，Dirichlet kernel，Fejér kernel，Poisson kernel

O173.1

A

1008-5513（2015）03-0238-07

10.3969/j.issn.1008-5513.2015.03.003

2014-08-23.

上海市一级学科建设项目.

王志珍（1974-），博士，副教授，研究方向：鲁棒控制，图像处理，数学分析.

2000 MSC：40C99