凹角区域泊松方程边值问题的CEFE与NBE耦合法求解*
朱双彪
(南京财经大学应用数学学院,江苏 南京 210023)
许多科学问题都可以转化为偏微分方程问题.通过数值求解这类问题的方法有很多,自然边界元[1-3]与有限元耦合法就是其中的一类.耦合法的好处在于,2种方法结合时能够弥补各自的不足.利用耦合法不仅可以求解圆和椭圆区域问题,还可以求解凹角区域问题[4-5].但在求解耦合问题时,由于是用直边三角形作有限元分析的,因此会产生误差.采用曲边有限元即曲边三角形代替直边三角形[6-8],就可以大大降低误差.笔者拟给出凹角区域上求解泊松方程边值问题的曲边有限元和自然边界元的耦合法.
1 曲边有限元与自然边界元耦合法
如图1所示,取夹角α、线段Γ0和Γ1、光滑的圆弧Γ,一起围成区域Ω.在区域Ω内求解如下边值问题:
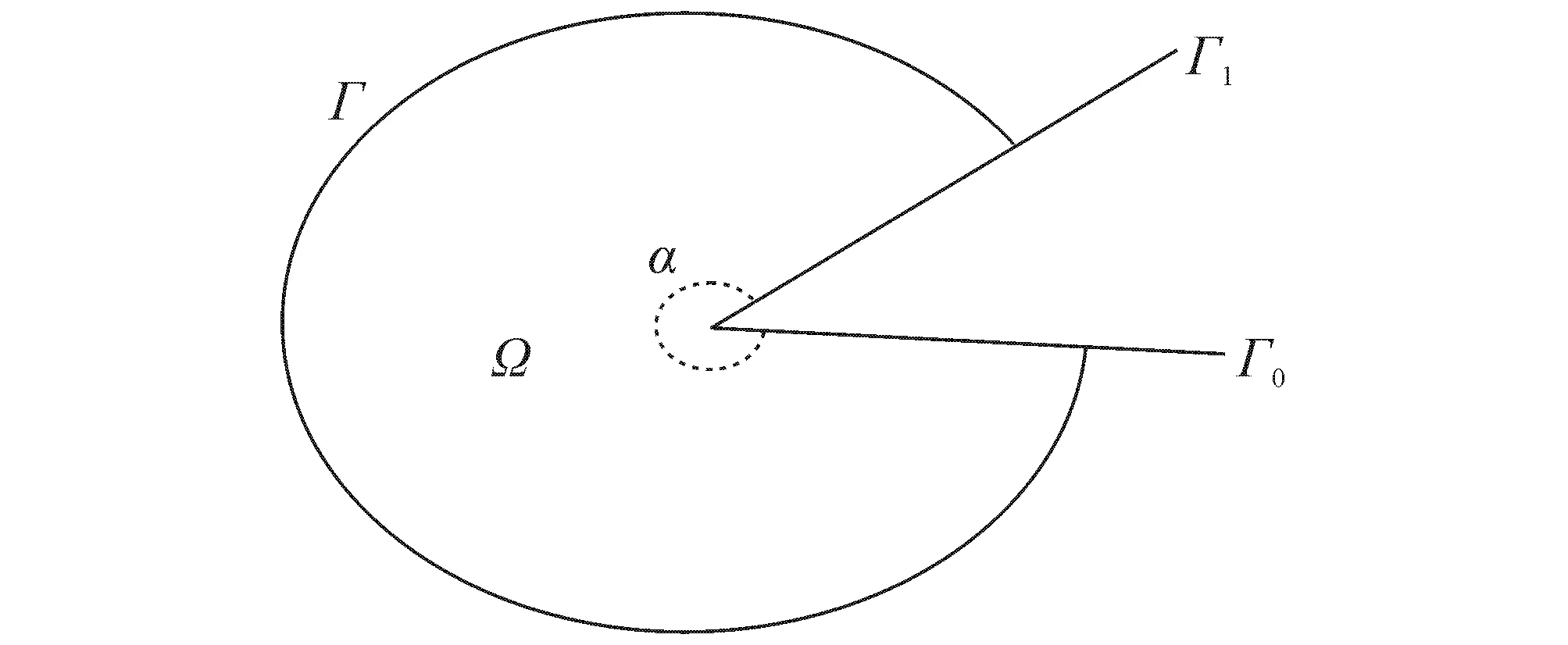
图1 区域ΩFig. 1 Area Ω
(1)
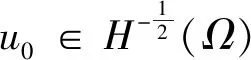
(2)
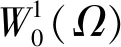
用半径为R的人工圆弧Γ2置于区域Ω内,其中Γ2={(R,θ)|0≤θ≤α},且dist(Γ,Γ2)>0.Γ2将区域Ω分为2个区域,Γ2包围的区域为Ω2,Γ2和Γ包围的区域为Ω1,如图2所示.在区域Ω2内用自然边界元方法,在区域Ω1内用曲边有限元方法.
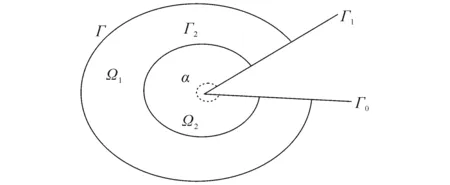
图2 区域Ω引入人工边界Fig. 2 Artificial Boundary of Area Ω
在耦合法中,一般是用直边三角形近似划分有限区域,但这种处理方式存在一定的误差.采用曲边元素,就可以很好地拟合待求解区域弯曲的边界[4-5].
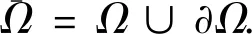
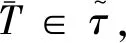
(3)
取参考单元G,其顶点g1=(0,0),g2=(1,0),g3=(0,1).记面积坐标(λ1,λ2,λ3),于是得到如下线性变换:
其中λ1=1-ξ-η,λ2=ξ,λ3=η.作如下变换F:
(4)
其中
(5)
(6)
这里
线性变换(3)~(6)可以将参考单元的3条边一一映射为曲边三角形的2条直边和1个曲边[6].
σ={Ni:i=1,2,3},是一组线性函数.定义Ni(φ)=φ(pi),φ∈Σ,i=1,2,3.在τ和有限元正则的情况下,各个曲边三角单元的插值误差估计为
(7)
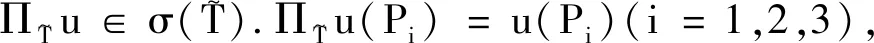
2 曲边有限元与自然边界元凹角耦合法的收敛性和误差估计
变分问题(2)的离散问题是
(8)
变分问题(8)有唯一的连续依赖于f的解.
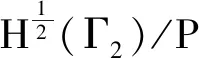
引理1[1]
证明因为Sh∈H1(Ω1),所以在
中取v=vh∈Sh,再与
相减,得到
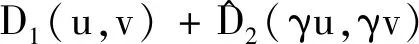
又因为uh∈Sh,所以
证毕.
由引理1和(7)式可以得到定理1,2:
定理1(收敛性) 假设插值算子满足
那么
定理2(能量模估计) 设u∈H2(Ω1),那么
由定理1给出的近似解满足收敛性可知,通过自然边界元和曲边有限元耦合法求解问题(1)是可行性.
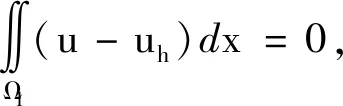
‖u-uh‖L2(Ω1)≤Ch2‖u‖2,Ω1.
对比能量模估计和L2模估计,L2模估计是最优的.
3 数值实例
例1在图1中取夹角α=7π/4.采用曲边有限元与自然边界元耦合法求解如下外边值问题:
其中Γ0,Γ1,Γ的边界条件分别为
Γ0={(r,θ)|r≥3,θ=0},Γ1={(r,θ)|r≥3,θ=α},Γ={(r,θ)|r=3,0<θ<α},
人工边界为
Γ2={(r,θ)|r=1.5,0<θ<α}.
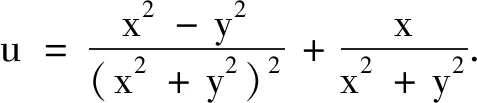
通过Matlab软件对区域进行加密剖分,结果如图3,4所示.图3是将边界划分为33个节点,图4是将边界划分为17个节点,可以看出图3的剖分比图4更密.
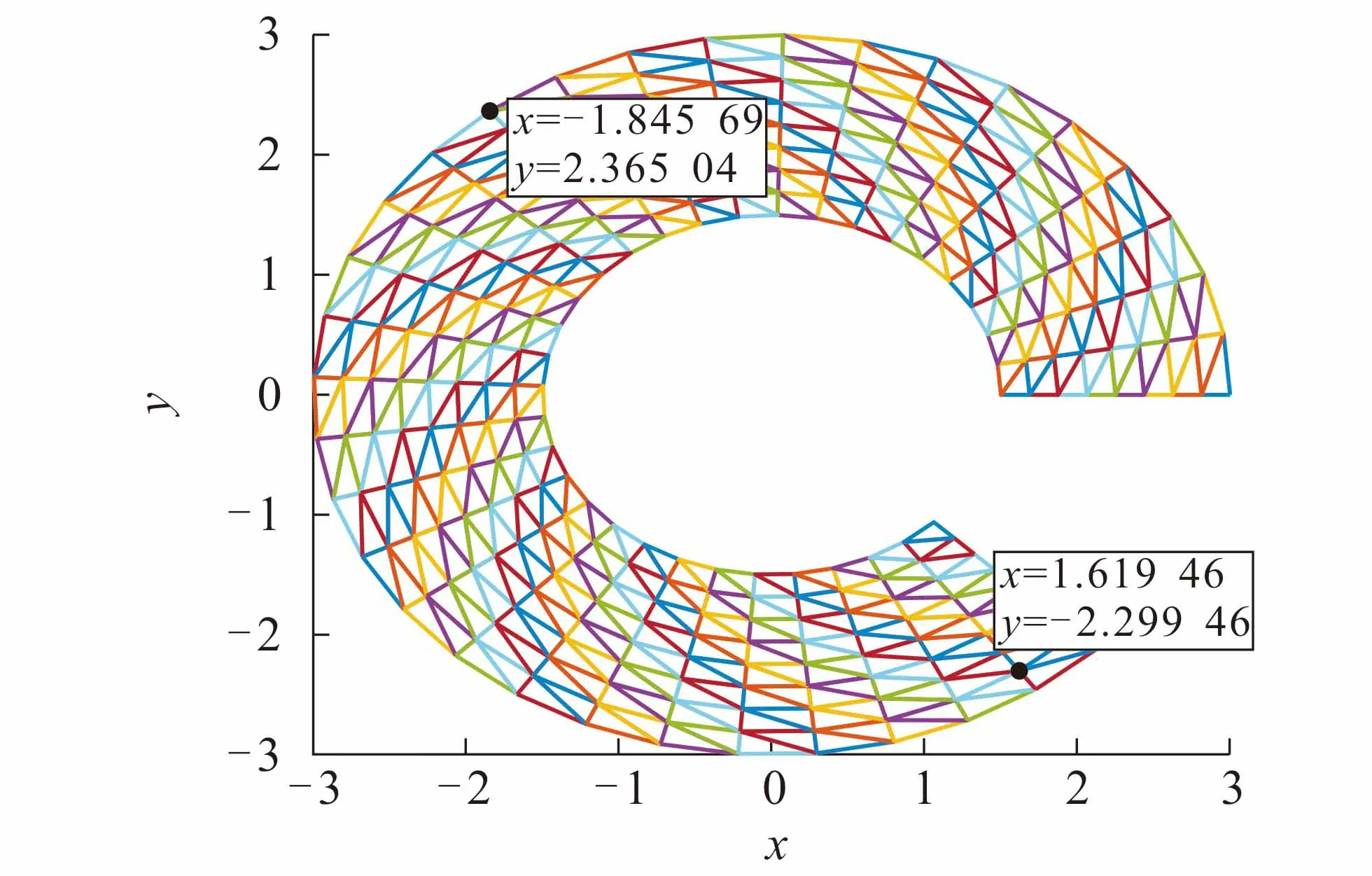
图3 mesh=8×33Fig. 3 mesh=8×33
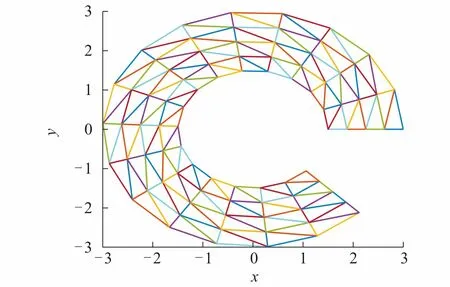
图4 mesh=4×17Fig. 4 mesh=4×17
取剖分网格N=17,33,65,129.有限元采用直边三角元和曲边三角元产生的误差分别见表1,2.

表1 有限元采用直边三角元产生的误差Table 1 Error Value of Straight Triangular Element in Finite Element

表2 有限元采用曲边三角元产生的误差Table 2 Error Value of Curved Edge Element in Finite Element
从表1,2可知:误差随着剖分网格的加密越来越小;当剖分网格相同时,L2误差阶都接近于ο(h2),但有限元采用曲边三角元产生的误差比直边三角元的小.这说明,曲边有限元采用曲边三角单元代替原来的直边三角形,可以克服边界近似产生的误差,降低数值积分误差.

