网络便利样本的推断问题研究

王 俊，金勇进，司亚娟

（1.中国人民大学a.统计学院；b.应用统计科学研究中心，北京100872;2.威斯康星大学麦迪逊分校生物统计及医疗信息系,美国 威斯康星州 WI 53726）

0 引言

随着人们生活节奏的加快、对信息安全的担忧等因素的影响，传统的概率抽样的回答率持续降低、花费越来越高，并且任何试图增加回答率的措施的单位成本也急剧上升。随着回答率的持续降低，研究人员不得不开始怀疑这些概率样本的代表性。与此同时，随着互联网的发展，网络便利调查成为了一种更为便捷、快速、便宜的收集调查数据的方式，常见的网络便利调查包括自我选择式网络调查、网络志愿样本池调查。

自我选择式网络调查中，调查研究人员直接将问卷的链接在各大互联网平台贴出，由上网的人群中感兴趣的网民自行选择参与调查。而对于网络志愿样本池调查来说，研究人员首先通过各种方式招募（通常为非概率抽样方法）大量的志愿者组建网络志愿样本池，当需要进行市场调研或者民意监测时，则根据一定的概率抽样设计从网络志愿样本池中抽取一个随机样本。

这类基于非概率抽样方法的网络便利调查，在获取样本单元的过程中并不依靠特定的抽样设计，而以招募受访者的便捷性考虑为主，通常情况下，能够在短时间内以较低的费用获取大量的样本单元。但对这类网络便利样本而言，由于最终样本是网络总体单元自我选择参与网络调查的结果，调查研究人员无法控制整个样本选择的过程，因此无法像概率抽样设计那样计算样本单元包含概率，进而不能直接在基于设计的推断框架下外推至总体。然而基于设计的推断方法由于其简单、方便、易操作而得到的广泛的应用，所以如何估计网络便利样本的包含概率则是对网络样本单元进行过推断的一个非常重要研究方面。

Rosenbaum(1987)[1]考察了倾向得分方法在非随机样本统计推断中的应用，在其背景中，倾向得分解释为总体中的单元被选进入非随机样本的概率，并将估计出的倾向得分的倒数作为非随机样本单元的权数，进而构建有限总体的HT估计量。在网络便利样本的推断中，由于无法获取总体单元层面所有的辅助信息，通常利用参照样本来估计总体中的单元被选入网络便利样本的概率，即倾向得分。参照样本可以是现存的质量更高的概率样本，或与网络便利调查同期执行的、质量更高的、至少包含用于构建倾向得分模型的变量信息的随机电话拨号调查。

Terhanian(2000)[2]，Lee(2006)[3]，Lee(2009)[4]将电话随机拨号调查获取的样本作为参照样本，并将其和网络便利样本融合成一个样本。合并后的样本中，网络样本单元的指示变量为1，参照样本单元则为0，通过简单逻辑回归估计出单元的倾向得分。这些方法在估计倾向得分的过程中，直接忽略了参照样本单元的设计权数。此时，利用逆倾向得分构建的网络便利样本单元的权数，只能将网络便利样本还原到合并后的样本，估计出的倾向得分只能解释为合并后样本中的单元被选入至网络便利样本中的概率，而非待研究的目标总体的单元被选入网络便利样本中的概率。Valliant(2011)[5]进一步探讨了逆倾向得分在构建网络样本池调查样本单元权数中的应用，通过实证研究和严格的数学证明，认为在利用参照样本和网络样本池样本估计倾向得分的过程中，需要将二者样本单元的权数考虑进逻辑回归模型的估计过程，形成加权的逻辑回归，并且将网络样本单元从参照样本的抽样框中剔除，否则将会导致估计量的偏差。然而在调查实践中，如果参照样本是现存

的高质量的概率调查，则对于普通的数据使用者来说，通常无法获取全国层面的抽样框，即使存在全国个人层面的抽样框，由于隐私问题，也无法获取参与调查者的身份识别信息，因此Valliant(2011)[5]提出的方法在实际操作中将存在困难；此外，其估计出的倾向得分的实际含义也模糊不清。本文在参照样本的背景下，考察如何利用逆倾向得分构建网络便利样本的权数，以对目标总体的特征进行统计推断，并在Valliant(2011)[5]提出的方法的基础上，将通过设计权数还原后得到的参照样本作为“伪总体”，并基于k最近邻的方法将网络便利样本单元从“伪总体”中剔除，此时，网络便利样本则可以看成是来自“伪总体”的一个样本，并通过加权的逻辑回归估计出倾向得分，估计出的倾向得分则可以解释为“伪总体”中的单元被选入至网络便利样本的概率，并将估计出的倾向得分的倒数作为网络便利样本单元的权数。

1 倾向得分及其在非随机样本推断中的应用

倾向得分方法是由Rosenbaum(1983)[6]在观测研究中为了有效估计治疗效应而提出的方法，在此背景中，倾向得分为观测样本单元在给定协变量X条件下，接受治疗T=1的概率 πi=P(Ti=1|Xi;γ)，当 πi满足下列条件(1)、(2)时:

(1)∀yi，P( )Ti=1|xi，yi;γ=P(Ti=1|xi;γ)

(2)∀vi，0 ＜ πi=P( )Ti=1|xi;γ＜1

则称单元进入治疗组或者控制组的分配机制为强可忽略的，即在给定X的条件下，观测样本单元被分配到治疗组T=1还是控制组T=0是完全随机的，和待研究变量y不相关，且均有一个非0的概率被分配到治疗组。此时，平均治疗效应（ATE）的估计为：

通常情况下πi的值是未知的，可以通过Logistic回归或Probit回归估计后带入式（1），进而得到。其实质则是分别利用治疗组和控制组的样本构造HT估计量，以估计样本层面的待研究变量的特征，二者的差异则为样本层面的治疗效应。在抽样调查的背景下，P(T=1|X;γ)则称为样本选择机制，T=1则目标总体中的单元被选入至样本，表示总体中的单元被选入样本的包含概率。

Rosenbaum（1987）[1]探讨了利用倾向得分对非随机样本s进行结构调整的方法，并假设 πi=P(i∈s|Xi;γ),i∈U为总体U中的单元被选入样本的包含概率。通过Logistic回归估计出参数γ̂，进而得到估计出的倾向得分，进而形成类似于HT估计量的逆倾向得分加权估计量：

2 基于k最近邻匹配的样本合并方法

2.1 基于k最近邻匹配的样本合并方法介绍

假设参照样本sr通过样本单元权数di，i∈sr还原得到的总体̂为伪总体，由于sr为概率样本，因此协变量X的设计无偏估计为，̂则可以看成是通过基于设计的估计过程得到的估计出的目标总体抽样框。网络便利样本sw，权数为（当为网络志愿样本池调查时，根据从网络志愿者样本池中抽取样本的不同，可能不为1，自我选择样本则均为1）。估计网络便利样本的包含概率则近似为估计网络便利样本单元从伪总体Û中被选入至sw的概率。为了集中考察方法，本文假设参照样本和网络便利样本均包含了协变量X的测量，且不存在模式效应，参照样本不存在无回答、涵盖误差等问题。估计过程见图1。

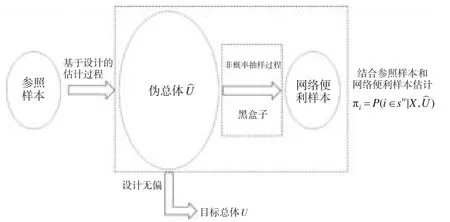
图1 估计过程

为了估计 πi=P(i∈sw|X，̂)，则需要将伪总体Û拆分为{̂-sw，sw} 。Valliant(2011)[5]认为应当将网络便利样本sw中的单元从参照样本的抽样框中剔除，然后将参照样本单元的权数均乘以（其中N为目标总体的规模）。然而在实际操作过程中，对于大多数调查人员来说，无法获取参照样本的总体抽样框，因此实际应用中存在困难，另外一方面如果参照样本是通过复杂抽样设计获得的，简单将参照样本的权数乘以将会导致协变量X分布的改变，更为重要的是其估计出的倾向得分的含义模糊不清。

然而在强可忽略的假设下，有 ∀yi，P(Ii=1|xi，yi;β，γ)=P(Ii=1|xi;β)，此时研究变量yi在网络便利样本sw中的分布f(yi|xi，sw;β)满足：

即控制了协变量Xi后，样本中待研究变量yi在网络便利样本sw中的分布f(yi|xi，sw;β)和其在总体中的分布f(yi|xi;β)一致，如果网络自愿样本sw中的第i个单元的协变量Xi和参照样本sr中的第j个单元的协变量Xj相同，则其待研究变量y的条件分布也相一致，此时，从伪总体̂中剔除一个和Xi相同的单元，则等同于将对应参照样本中的单元j的权数dj更新为dj-，更新后的权数不改变合并后的样本的辅助变量X及待研究变量y在伪总体中的结构及分布。最理想的情况是，网络样本sw中的每个单元都能够在参照样本sr中找到对应的精确匹配的单元，伪总体̂则拆分为{̂-sw，sw}。但是实际应用中，一方面，网络样本的样本量通常较大，而参照样本的样本量通常较少，因此网络样本中的单元并不是都能够在参照样本中找到精确匹配的单元；其次，满足一对一式的精确性匹配的样本单元往往较少，如果仅使用匹配后的样本单元，将会造成网络样本单元的大量浪费；此外，如果使用1最近邻的方法进行匹配通常会受到异常值的影响，尤其是当参照样本和网络样本之间协变量分布存在较大差异的时候。因此，本文基于kNN方法提出基于距离的加权的权数调整及样本插入的方法，过程如下所示：

步骤1：计算距离函数，并选择最近邻的k个单元。假如sw中第i个单元根据协变量Vi在参照样本sr中的k最近邻单元集合为Ni，k：

其中d(Vi，Vj)为距离函数，本文选择欧氏距离。

步骤2：单元插入及权数更新。由于本文中原始网络样本单元的权数为，对于网络样本中第i个单元在参照样本中的k个邻近单元Ni，k中的第c个单元（参照样本中的第j个单元）的权数dj更新为：

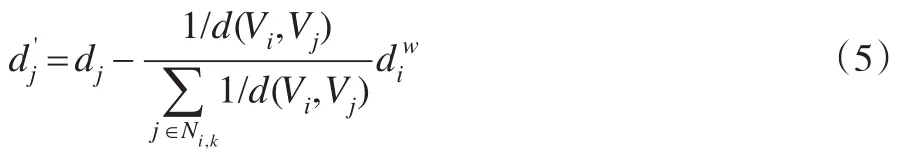
此时，Ni，k中的k个单元更新后的权数，(j∈Ni，k)的和为：

网络样本中的第i个单元，则相应地插入到参照样本中，权数为，则第i个单元的网络样本单元的权数和Ni，k中的k个单元的权数和为即参照样本和非概率网络样本融合后，不改变原始参照样本单元权数和。

步骤2的实质是将网络样本单元的权数按比例从其在参照样本中最近邻的k个单元的原始权数dj中扣除。重复步骤1和步骤2，直到所有的网络样本单元均被插入参照样本。则最终合并后的样本单元s={sr'，sw}，相应的权数为

根据步骤2，可以得到最终合并后样本s中单元的权数有：

即通过权数可以将合并后的样本集合在规模上依然还原至目标总体U。

步骤3：令Ii=1，i∈s表合并后样本s中第i个单元属于网络样本sw，Ii=0，i∈s表合并后样本s中第i个单元属于网络样本sr'。使用加权逻辑回归估计合并后样本s中单元被选入网络样本sw的概率π̂i。则网络样本单元的权数为wi=1，总体均值的估计为：

2.2 最近邻匹配个数k的选择

根据模拟的结果发现，步骤1中随着最近邻匹配个数k的增加，的相对偏差（定义见式（14）），随着k的增加不断减小，并最终趋向于稳定，的标准差（定义见式（10））、离散系数（CV）随着k的增加先增加后减小并趋向稳定。以上述模拟过程中的一次为例（如图2），随着k的增加估计量的相对偏差的绝对值变化相对较小，当k=2 时，估计量的相对偏差、CV最小，因此，本文中选择使得的标准差或者CV最小的k。

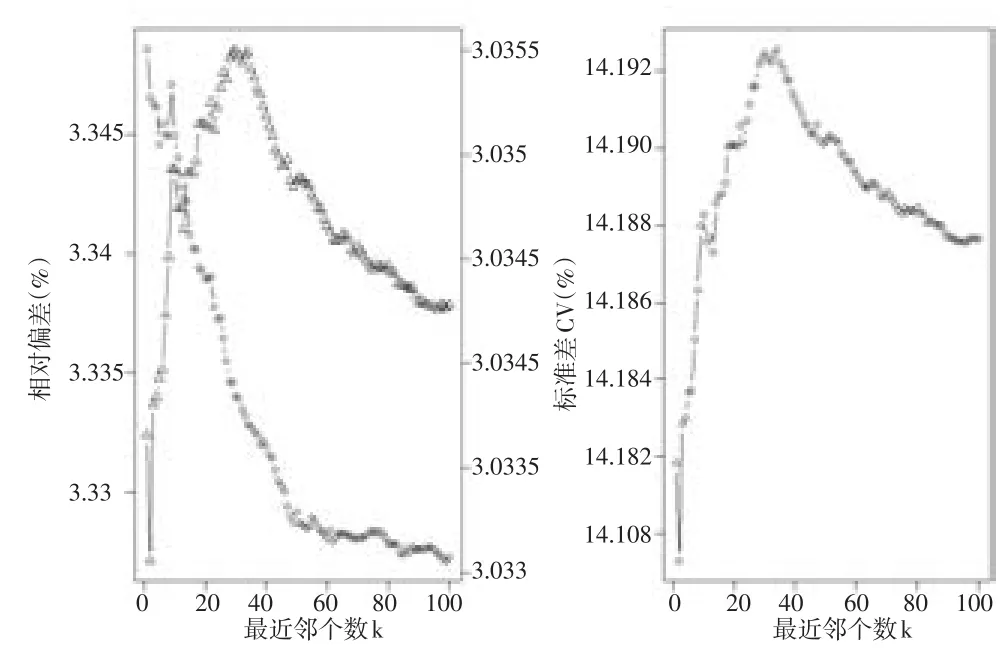
图2 最近邻个数k的选择

2.3 估计量的方差估计

的方差的估计为：

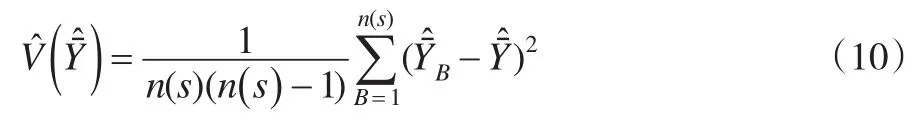
3 模拟研究

由于不同的调查模式之间会存在模式效应，比如纸笔调查和网络调查、电话调查和网络调查等，为了消除这种模式效应，并集中于研究不同倾向得分权数调整方法在网络自愿样本推断中的效果，在本文的模拟研究中，使用2014年中国家庭追踪调查（CFPS）的成人调查数据，删除个案缺失数据，及对相关变量进行随机插补后，一共有14039个个案，其中可以上网的个案有4084人，不可以上网的有9955人。为了减少抽样比较高引起的高估估计量效率的影响，本文利用有放回式的简单随机抽样从14039个个案中抽取1000000次，每次抽取一个单元，并将这1000000个个案作为模拟总体U。中国家庭追踪调查（CFPS）是由北京大学社会科学调查中心组织的旨在了解中国社会、家庭及个人发展的全国性的概率调查，每年进行一起。在CFPS的问卷中，他们设计了一个问题可以识别出样本单元是否上网，因此，使用CFPS的数据可以方便本文问题的研究。此外，本文通过对模拟总体数据进行逐步回归选取了所在省份prov、地区类型urban、年龄age、性别gender、受教育年限eduy、户籍类型qa作为解释总体单元能不能上网的协变量，并为每个模拟总体U中的单元模拟了三个连续性变量x1，x2，x3，三个变量分别来至于均值为10,5,40,方差为9,9,9的正态总体，并将上述9个变量作为估计倾向得分的解释变量，待研究的变量y由下面的模型生成：

3.1 模拟过程

步骤1：利用无放回式简单随机抽样从总体U中抽取一个样本量为nr的参照样本；

步骤2：从总体U中可以上网的子总体UW中根据指定的样本选择机制：

抽取样本量nw的网络自愿样本，其中=1表示子总体UW中第i个单元被选入到样本，假定非概率网络样本的样本选择机制为Logistic形式：

步骤3：对于特定的参照样本和网络样本的样本量组合nr，nw，重复步骤1和步骤2抽样过程1000次，每一次抽样过程后，均计算以下估计量：

（1）将基本人口信息变量省份、地区类型、年龄、性别、受教育年限及户籍类型作为辅助变量产生线性校准估计量

（2）将式（8）中的所有变量作为辅助变量产生线性校准估计量

（3）忽略参照样本单元权数的简单逻辑回归得到的逆倾向得分加权估计量

（4）Valliant提出的加权逻辑回归得到的逆倾向得分估计量

（5）本文提出的逆倾向得分加权估计量

本文从平均相对偏差（R.Bias）、平均标准差（S.E）及95%置信区间包含真值的比例（Coverage rate）三个方面对不同的估计量进行比较。

平均相对偏差定义为：

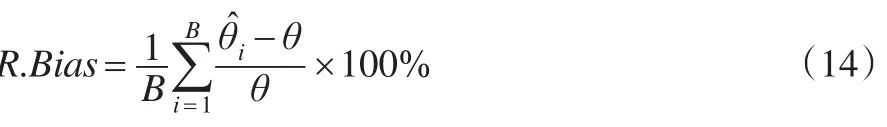
其中B为对于每次实验过程重复的次数，本文中B=1000，̂为第i次实验得到的总体特征的估计，θ为总体特征真值。

平均标准差定义为：

其中为第i次重复实验得到的估计量的标准差。

95%置信区间包含真值的比例定义为：

其中Interval为第i次模拟过程构造的置信区间。

步骤4：为了研究不同样本量nr,nw对估计结果的影响，本文赋予nr，nw不同的样本量组合，如表1所示：

表1 不同的样本组合

表中“√”表示有效的实验组合，“×”表示本文未做该样本组合的模拟研究。相比较于网络调查，传统的概率抽样花费较为昂贵，因此在本文的模拟研究中，限定参照样本的样本量不多于网络自愿样本的样本量。对于不同的nr和nw，重复步骤1至步骤3。

3.2 结果

从表2（见下页)可以看到，估计倾向得分模型时，如果忽略参照样本的设计权数，直接利用简单逻辑回顾，则得到的逆倾向的分加权估计量平均相对偏差较大，均在-10%以上，当网络便利样本量固定时，随着参照样本量的增加，的平均相对偏差有减少的趋势，但仍高于-10%，此时，网络便利样本样本量的增加并不能有效减少此估计量的平均相对偏差；Valliant提出的使用参照样本的设计权数，通过加权Logistic回归得到的逆倾向得分估计量以及本文提出的基于kNN的样本合并方法得到的逆倾向得分估计量的平均相对偏差较小，均在5%以内，当网络便利样本的样本量为2000时，两种估计量的相对偏差几乎相同，网络便利样本的样本量增加到3000时，的平均相对偏差均小于。

表2 不同样本组合下估计量相对偏差R.Bias结果

从95%的置信区间包含真值比例方面来看（见表3），的95%的置信区间包含真值的比例较低，在本文的模拟研究中均不高于90%；及95%的置信区间包含真值的比例均接近95%，当网络便利样本的样本量固定时，随着参照样本量的增加，两种估计量的95%置信区间包含真值的比例，有微弱的下降趋势，比如当网络样本量为3000时，随着参照样本量从500增加到3000，的95%置信区间包含真值的比例由95.1%下降至93.9%。

表3 不同样本组合下估计量95%置信区间C.Rate结果

从平均标准差SE来看，在网络便利样本的样本量固定的条件下，随着参照样本的增加（见表4），及的标准差逐渐减少，而对于忽略样本单元权数的简单逻辑回归得到的逆倾向得分加权估计量却有增加的趋势。

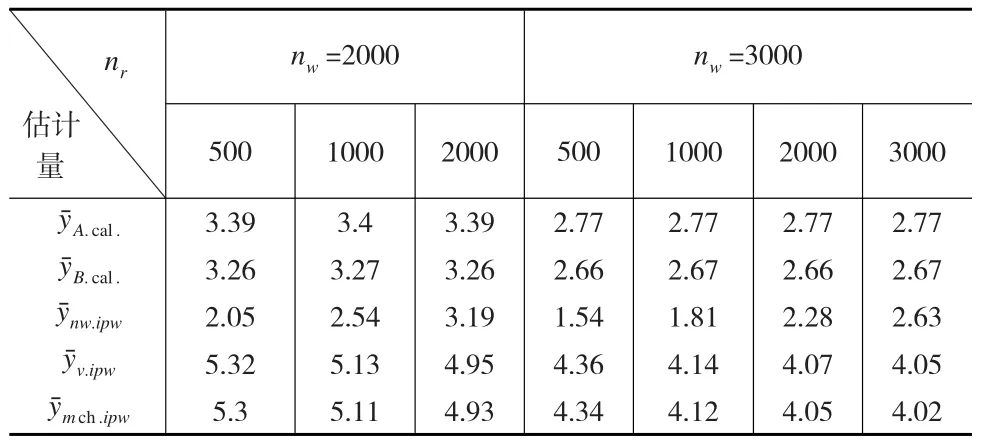
表4 不同样本组合下估计量标准差SE结果

值得注意的是，当校准变量为生成y的模型中所有变量时或者部分人口信息变量时，校准估计能够显著减少估计量的偏差，但不能完全消除偏差。然而校准变量的选择必须与待研究变量高度相关才能达到减少估计量偏差的效果，本文中选择的校准变量为生成待研究变量模型中的一部分或者全部，因此校准估计的模拟结果与其他方法相比具有较高的效率。

4 结论

本文在网络便利样本的背景下，介绍了倾向得分及其在利用网络便利样本对目标总体进行推断中的应用，并提出了基于k-NN的样本合并方法及相应的逆倾向得分估计量。模拟结果表明在估计倾向得分模型时，如果不考虑样本单元的权数，构建的逆倾向得分估计量的偏差相对较大、95%置信区间包含比例也较低；本文提出的基于k-NN样本合并方法及对应的逆倾向得分估计量，与Valliant提出的方法相比，在实际使用过程中，具有更高的操作性，且当网络便利样本的样本量较大时，能够相对减少估计量的偏差。此外，相对于利用倾向得分构建权数的方法，当将生成待研究变量y的所有协变量都包含进校准模型时，校准估计的平均偏差最小，随着样本量的增加平均偏差趋向于0。当校准模型中只包含基本的人口信息变量时，虽然相对于未截取的逆倾向得分估计量有所减低，但不能完全消除偏差。