权数可靠性的假设检验探讨
谢忠秋
(江苏理工学院 商学院,江苏 常州 213001)
1 问题的提出
根据研究,赋权方法已多达20多种。受此影响,即使是运用同一数据、同一无量纲化方法以及同一综合评价方法,而由于各人选择赋权方法的不同,也会致使综合评价的结论大相径庭。因此,如何对众多赋权方法所得权数的可靠性进行科学界定,就显得十分必要。
从现有文献看,关于权数的研究主要集中在以下几方面:(1)赋权方法的研究。这也是目前权数研究的主要内容。有主观赋权法、客观赋权法、组合赋权法等多达20多种赋权方法。(2)权数的性质研究。在权数具有重要性、模糊性、主观性、时序性的基础上,提出了空间性、时空性和函数性等权数新的性质,进一步深化了对权数的理论思考。(3)权数的调整研究。包括对抽样调查分析中初始权数的调整以及依据方差控制要求的权数调。(4)对权数影响的研究。如无量纲化对属性权重的影响,之间存在一种传导机制等。显然,上述研究进一步丰富和发展了权数的理论和实践体系。然而,在上述研究中,忽略了权数研究的一个根本性问题,即权数的可靠性研究。事实是,只有当权数可靠了(同样,在无量纲化和综合评价方法方面也存在着可靠性的问题),才能带来综合评价结果的正确性。相反,容易致使人们对其产生“怀疑”,进而对综合评价结果也极易产生一种“不信服”感,从而严重影响着综合评价的声誉。所以,在赋权方法的选择上,应以所得权数是否具有可靠性为标准。可靠,则该赋权方法可用,所得权数可用。否则,则俱不可用。显然,在权数研究中,应补上权数可靠性研究这一重要内容。但迄今为止,有关权数可靠性研究的文献还没有。也正基于此,本文提出这一问题,并给予实例分析,以期弥补权数研究现有的不足。
2 权数可靠性检验的统计量
所谓权数可靠性,从统计学的角度来说,就是指能以多大的概率保证依据某一赋权方法所得出的权数与评价者期望的权数相一致。显然,概率越大,则意味着依据某一赋权方法所得出权数的可靠性越好。在统计上,解决此问题的路径是进行权数可靠性的假设检验。
为便于理解,本文建立原假设H0:采用某一赋权法所得权数与总体权数没有显著差异(没有差异,则意味着所得权数是具有可靠性),则有:备择假设H1:采用某一赋权法所得权数与总体权数有显著差异(有差异,则意味着所得权数不具有可靠性)。而做好权数可靠性假设检验的核心是确定检验所用的统计量。
考虑到权数具有计数的性质,而卡方检验又是一种用途很广的计数资料的假设检验方法。所以,可以运用χ2检验,统计量如下:
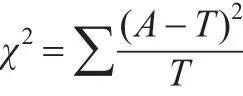
式中,A:实际数,T:理论数,V:自由度,为(行数-1)×(列数-1)
总体权数是客观存在的,相当于公式中的实际数,而运用某一赋权方法所得出的权数则相当于公式中的理论数。如果说,χ2检验的根本思想在于比较理论频数和实际频数的吻合程度问题,那么,权数的χ2检验的根本思想就在于比较运用某一赋权法所得权数和客观存在的总体权数的吻合程度问题。显然,如果总体权数已知,则可以直接运用检验。但事实毕竟是,总体权数事先是未知的,这就使得直接运用进行检验无法实现。那么,能否通过一定的变换,找到的替换变量,从而完成权数可靠性的假设检验呢?经过推导,证明这一想法是可行的。
χ2=的替换变量的寻找过程如下:
设:maxT-T=λi(maxT-minT)
λi是指样本的最大权数与某一权数的离差占总离差(极差)的比例。
于是有:
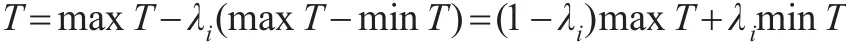
进一步有:
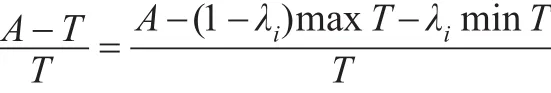
分子两边平方:
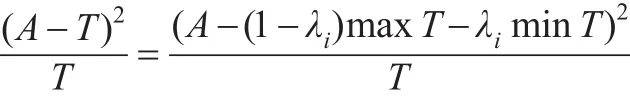
由于:
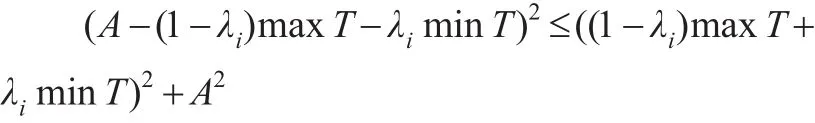
而:
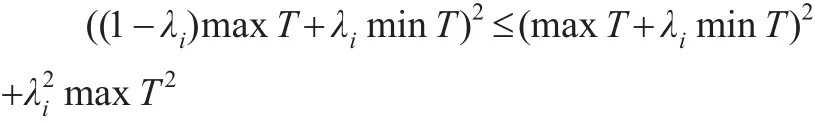
所以:

从而也有:
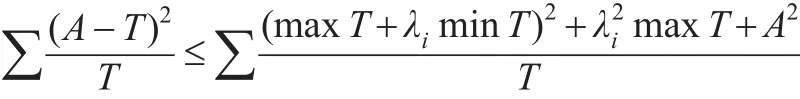
在非负数的情况下,又有:
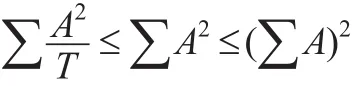
由权数的性质可知,∑A=1,所以有:
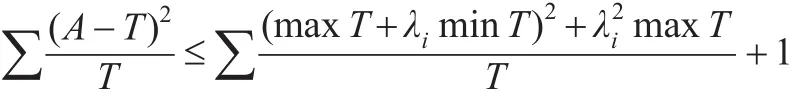
取最大值,则有:
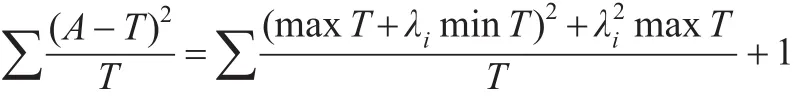
最终有:
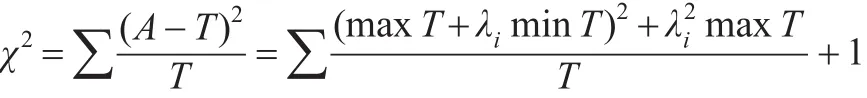
所以,对权数可靠性进行假设检验,其步骤如下:
(1)建立原假设H0:采用某一赋权法所得权数与总体权数没有显著差异。
备择假设H1:采用某一赋权法所得权数与总体权数有显著差异。
(2)计算χ2统计量:
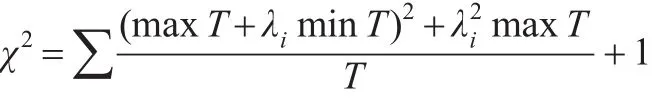
自由度v=(行数-1)×(列数-1)
(3)给定显著性水平(t(),查卡方界值表,找到(v)。
(4)比较χ2统计量与临界值χα2(v),当χ2≤χα2(v),则接受H0,拒绝H1,认为采用某一赋权法所得权数与总体权数没有显著差异;当χ2≥(v),则拒绝H0,接受H1,可以认为采用某一赋权法所得权数与总体权数有显著差异。
3 例证运用
例1和例2分别说明了权数可靠性检验接受原假设H0和接受备择假设H1的情况。结果表明,本文所提出的权数可靠性检验具有一般性。
例1:有6项指标,分别为A、B、C、D、E、F,采用某种赋权法所求得的权数分别为:0.2、0.15、0.16、0.18、0.11、0.2。那么,依据某种赋权法所得出的权数与总体权数之间是否有显著差异?计算过程见表1所示。
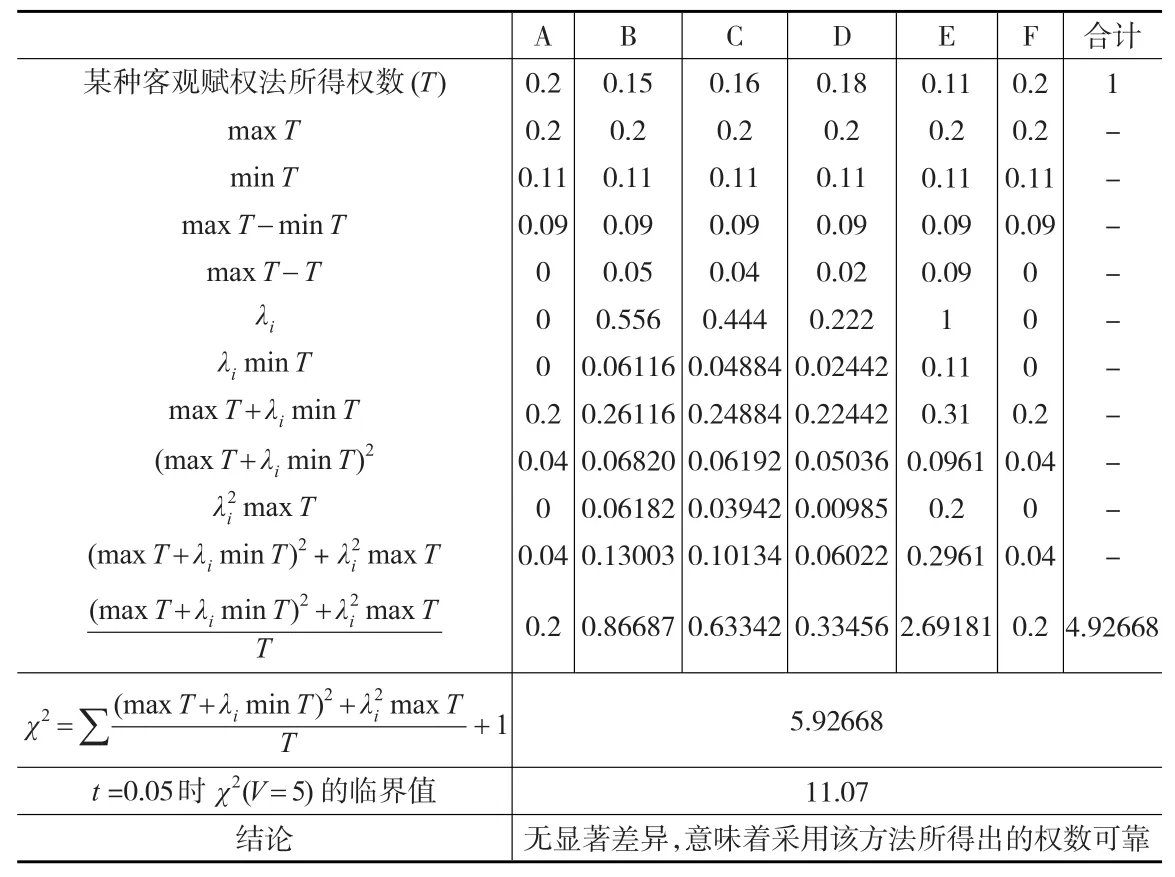
表1权数假设检验计算过程
例2:有6项指标分别为A、B、C、D、E、F,采用某种赋权法所求得的权数分别为:0.16、0.13、0.11、0.14、0.18、0.28。那么,依据某种赋权法所得出的权数与总体权数之间是否有显著差异?计算过程见下页表2。
需要指出的是,在实际运用时,要注意两个细节,一是权数的表现形式,不能采用∑T=100这样的形式,而只能采用∑T=1这样的形式,之所以如此,根本原因在于保持权数的和等于1这一性质不至于改变。二是在考虑列数或行数时,应将未知的总体权数的列数或行数考虑进去,否则会导致自由度是0而无法取得临界值。
4 结束语
本文通过运用上述方法对某种赋权法所得权数的可靠性进行检验,从根本上解决综合评价中权数确定无假设检
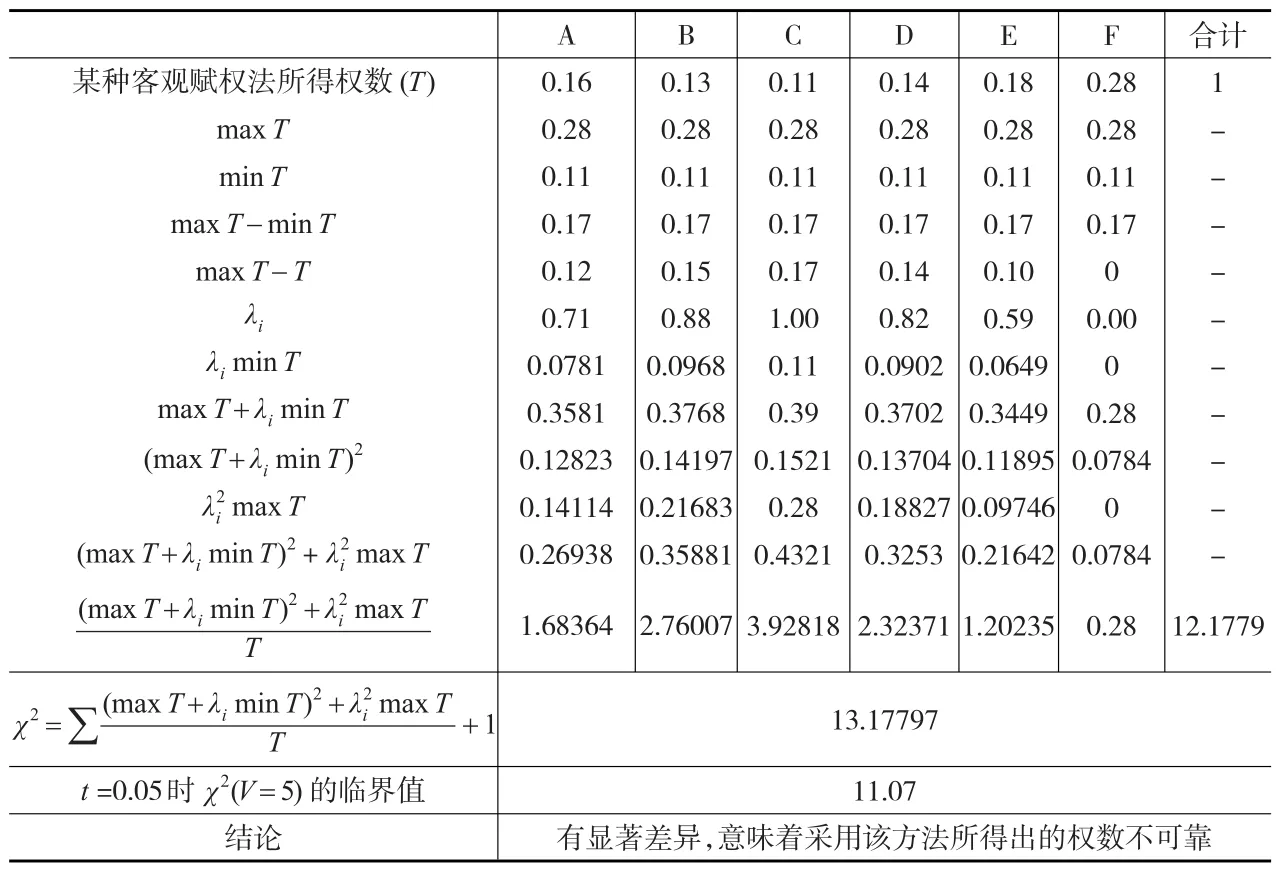
表2 权数可靠性检验计算过程
验的现象,以增强赋权法所得权数乃至综合评价的可信性。

