基于倾向得分多层模型的非概率抽样统计推断

刘 展

（湖北大学a.数学与统计学学院；b.应用数学湖北省重点实验室，武汉430062）

0 引言

网络调查由于其具有比电话调查更短的数据收集周期和更低的费用而急剧增长，目前已经在市场研究的调查数据收集中占主导地位。网络调查可视为一种单一的模式，但其抽取样本的方法有多种，包括基于概率抽样的网络调查与基于非概率抽样的网络调查，其中最值得注意的是基于非概率抽样的候选者数据库网络调查。这里网络调查的候选者数据库，简称网络候选者数据库，指自愿完成网络调查的上网人群，如果在后续的网络调查中选择他们作为调查对象，他们将配合完成调查[1]。候选者数据库网络调查是从网络候选者数据库中抽取样本进行网络调查，其获得的样本为网络候选者数据库的调查样本。可以看到，候选者数据库网络调查本质上属于非概率抽样调查，其样本属于非概率样本，入样概率未知，采用传统的抽样推断理论进行推断存在一定的困难。因此，非概率样本的统计推断问题，特别是候选者数据库网络调查的推断问题，就成为网络调查发展中迫切需要解决的问题。

倾向得分调整方法是一种被广泛应用于非概率抽样推断的方法。Duncan和Stasny（2001）[2]利用倾向得分方法降低了电话调查的覆盖偏差。Schonlau等（2004）[3]与Lee（2006）[4]指出倾向得分调整方法可能有助于减少抽样框覆盖不全、无回答、非概率抽样等产生的偏差。Brick（2013）[5]提出使用倾向得分加权来解决单元无回答的缺失问题。Schonlau 等（2009）[6]将性别、年龄、教育、收入等作为X，是否上网作为Y建立模型，构建非概率样本的倾向得分权数，最终得到的加权估计接近于总体参数真值。Valliant和Dever（2011）[7]结合网络候选者数据库和参考样本，建立logistic回归模型来估计倾向得分，并基于倾向得分对非概率样本构造了不同的权数来估计总体。然而，以上建立倾向得分模型估计倾向得分来推断总体均是在单一层次数据背景下进行的，即假设网络候选者数据库的数据结构是单一层次的，然而在一些情况下网络候选者数据库的数据结构可能是多层次或嵌套结构。多层次或嵌套结构就是在上一级分层的基础上进行再分层，形成一层套一层的嵌套结构或多层次结构，单一层次结构就是一个层次，不再逐层细分。例如，学生往往在一个班级内可以被分成不同的类，反过来这些班级又在学校内可以被分成不同的群。如果忽略数据的嵌套结构，仍然采用单一层次结构下的方法进行分析，可能会导致误导性或不准确的结果。因此，当网络候选者数据库数据具有嵌套结构时，需要考虑针对嵌套结构数据的倾向得分估计方法。Li等（2013）[8]在观察性研究中针对多层（嵌套）结构数据，探究了建立多层模型估计倾向得分来估计平均处理效应，但是并未探讨总体推断的问题。关于多层模型在医疗护理、卫生政策、教育等诸多领域中的应用研究文献越来越多，同时倾向得分分析也日益流行，然而对多层次数据结构的倾向得分分析还没有得到深入的研究。基于此，本文针对具有嵌套结构数据的网络候选者数据库和参考样本，探索构建倾向得分多层模型来推断总体的方法。为了便于讨论，本文主要考虑两个层次的嵌套结构数据。

1 多层模型

多层模型（Multilevel Modeling，简记为MLM）是包含固定效应和（或）随机效应的回归模型，是一种用于评价嵌套结构数据的统计分析方法[9]。多层模型是通过解释单元间的依赖关系、适当调整标准误差、在所有层次上分解方差，来改进嵌套数据中个体效应的估计。此外，多层模型允许跨层次的相互作用，这种相互作用解释了在一个层次测量的变量是如何影响在另一层次上所发生的关联的[9]。换句话说，对嵌套数据建立多层模型允许研究者去调查结果的变动有多少与群内和群间个体之间的差异有关[10]。下面讨论具体的多层模型方程。

对第j个群中第i个人观测的连续因变量Y的多层模型如下：

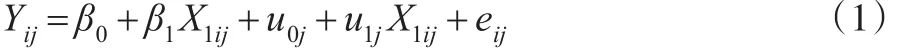
式（1）中β0、β1是固定效应，u0j、u1j为随机效应，eij为随机误差项。其中固定效应是未知的常数（参数），定义了预测变量X1ij与因变量Yij之间的关系；随机效应是随机变量，允许回归模型中的系数根据研究的群或个体（对象）随机变动，因此多层模型也称为随机系数模型。既然随机效应是随机变量，相应的就需要对随机效应定义概率分布，这就意味着多层模型比一般的回归模型有更多的参数需要估计。随机效应与随机误差项通常的假定分布为：

其中D为随机效应的方差协方差矩阵，为u0j的方差，为u1j的方差，σ01为u0j与u1j的协方差，σ2为eij的方差。

事实上，多层模型（1）也可以写成另外一种形式，如式（3）所示，式（3）是更为常见的一种形式，很多软件比如HLM、MLwiN等使用的都是这种形式。

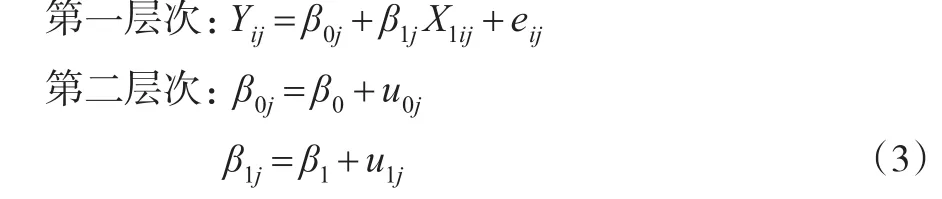
其中β0j、β1j为随机系数，并且β0j为第一层次方程的截距，β1j为第一层次方程的斜率，将第一层次与第二层次的方程结合即可得到式（1），第二层次中关于β0j的方程称为截距方程，关于β1j的方程称为斜率方程。式（3）清晰地定义了多层模型中第二层次所测量的第一层次预测变量，可以将第二层次的每个随机系数方程视为一个仅有截距项的回归模型，并且可以通过在这个模型中增加第二层次预测变量来解释随机效应的方差，比如在截距方程中增加性别Gender作为第二层次预测变量，则β0j=β0+β2Genderj+u0j，β2为未知常数（固定效应）。

式（3）只是一个简单的二层次模型，在具体建模时可根据具体的问题在第一层次方程中添加预测变量如X2ij，…，Xpij等，在第二层次方程中也可以添加一些预测变量。总之，在多层模型中预测变量可以被添加到第一层次和第二层次的模型方程中，这些变量的截距或斜率可以跨层次的变动，即截距或斜率可以为随机变量，是否限制或允许第一层次与第二层次预测变量跨层次变动是多层模型特殊的一个重要方面[9,11,12]。如果为三层次模型，则第二层次方程中的一些系数也是随机的，可以同样写出随机系数的第三层次方程，依次可类推到多个层次的模型。

对于多层模型的估计，可以从矩阵形式来考虑。在随机效应的条件下，第 j个对象或群的观测向量分布为 Yj|uj～N(Xjβ+Zjuj，Rj)，其中Xj为预测变量设计矩阵，β为固定效应向量，Zj为更小一些的预测变量设计矩阵，uj为随机效应向量，Rj为随机误差的方差协方差矩阵。所有随机效应平均下Y的边际分布为Vj)，其中Xjβ为第j个对象或群的观测Y的期望向量，D为随机效应的方差协方差矩阵对象或群的观测Y的边际方差协方差矩阵。在此基础上，采用某种形式的极大似然估计方法来估计模型参数。假设对象或群是相互独立的，首先写出似然函数形式为的边际概率密度函数，β、θ为待估参数，对有些模型来说似然函数可能需要近似。然后，使用迭代数学方法（比如Newton-Raphson）找到使得（近似的）似然函数值达到最大的模型参数估计。

2 倾向得分多层模型及总体估计

假设网络候选者数据库的协变量数据具有嵌套结构，比如协变量包括了班级、学校等变量，此时网络候选者数据库单元为不同学校不同班级里的学生。从该网络候选者数据库中随机抽取一个样本进行调查，得到一个网络候选者数据库的调查样本；同时假设获得了另一个具有同样嵌套结构数据的参考样本，比如采用多阶段随机抽样得到了另一个概率样本。设调查样本中第j个群第i个单元的入样概率 πij=π(Xij)，Xij=(Xij1，Xij2，…，Xijp)′是协向量，p是协变量数目，则有：

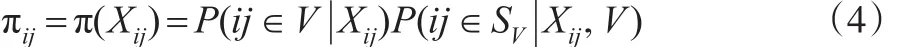
其中，V是网络候选者数据库；SV是从网络候选者数据库中随机抽取的调查样本；P(i j ∈ SV|Xij，V)是网络候选者数据库中第j个群第i个单元进入网络调查样本的概率，常常已知；P(ij∈V|Xij)是第j个群第i个单元自愿加入网络候选者数据库的概率，往往未知需要估计。设示性变量D表示单元是否加入网络候选者数据库，D=1记为单元加入网络候选者数据库，D=0记为单元未加入网络候选者数据库，那么第 j个群第i个单元加入网络候选者数据库的概率就是p(Xij)=P(Dij=1|Xij)=P(ij∈V|Xij)。

根据倾向得分的定义：给定辅助变量X的条件下单元接受处理（参与或回答）的条件概率，可知p(Xij)=P(ij∈V|Xij)本质上就是倾向得分。由于p(Xij)为一个概率，其范围在0到1之间，取值有限，直接建立多层模型不太合适，因此考虑使用联结函数，如最常用的Logit联结，即logit(p(Xij))=log(p(Xij)(1-p(Xij)))，将概率范围(0，1)转换为(-∞，∞)，再建立多层模型。在建立多层模型时，有很多的模型选择，比如第一层次的预测变量可以假定在群层次（第二层次）上是固定的或变动的；第二层次的预测变量可以仅包含在截距方程中，仅影响截距，也可以既包含在截距方程中，也包含在斜率方程中，同时影响截距和斜率。总之，在模型假定上进行不同层次预测变量的添减以及截距、斜率随机性的设置，就会产生许多不同的多层模型。下面分别进行讨论。

（1）具有固定斜率随机截距且不包含第二层次预测变量的倾向得分多层模型。

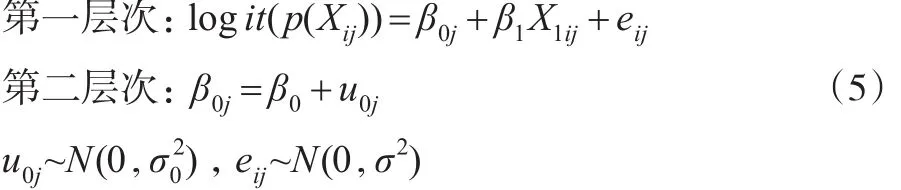
这里logit(p(Xij))表示倾向得分的Logit函数；β0为斜率方程中的斜率（固定）；β1为第一层次方程中的斜率（固定）。该模型假定不同群中X1与logit(p(Xij))回归方程的斜率相同截距不同，截距不同是由群的差异所引起的，但并未考虑群层次上具体变量对截距的影响。此模型通过固定斜率，假定X1对logit(p(Xij))的影响在不同群中是一样的。

（2）具有固定斜率随机截距且包含第二层次预测变量的倾向得分多层模型。

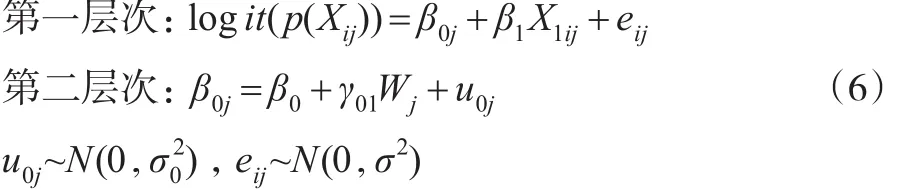
其中Wj为第二层次上的预测变量，γ01为固定斜率。此模型假定第二层次预测变量W只对X1与logit(p(Xij))回归方程的截距产生影响，换句话说不同群中X1与logit(p(Xij))回归方程的截距不同斜率相同，截距受到预测变量W的影响。

（3）具有随机斜率固定截距且不包含第二层次预测变量的倾向得分多层模型。

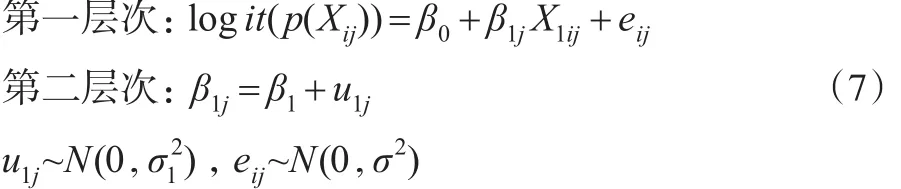
此模型假定不同群中X1与logit(p(Xij))回归方程的截距相同斜率不同，斜率不同是由群的差异所引起的，但并未考虑群层次上具体变量对斜率的影响。

（4）具有随机斜率固定截距且包含第二层次预测变量的倾向得分多层模型。

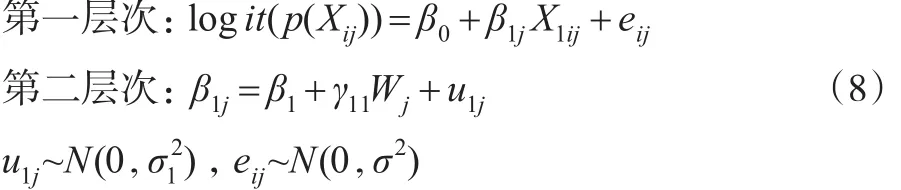
其中Wj为第二层次上的预测变量，γ11为固定斜率。此模型假定不同群中X1与logit(p(Xij))回归方程的斜率不同截距相同，斜率受到预测变量W的影响，即第二层次预测变量W对第一层次预测变量与因变量之间的关系产生影响。

（5）具有随机斜率随机截距且均不包含第二层次预测变量的倾向得分多层模型。

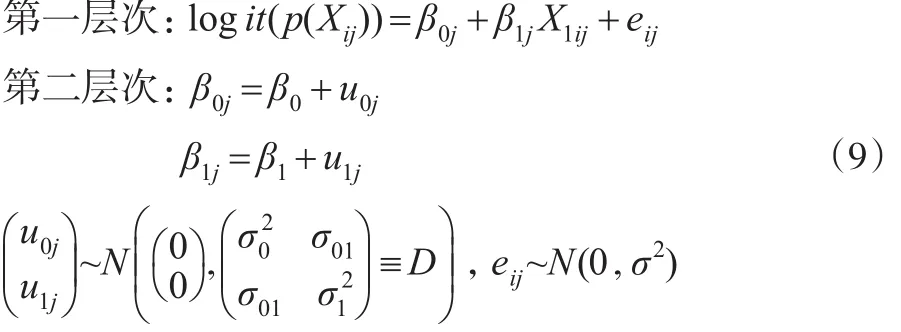
此模型假定不同群中X1与logit(p(Xij))回归方程的截距和斜率均不同，截距和斜率的不同是由群的差异所引起的，但并未考虑群层次上具体变量对截距和斜率的影响。

（6）具有随机斜率与截距且均包含第二层次预测变量的倾向得分多层模型。

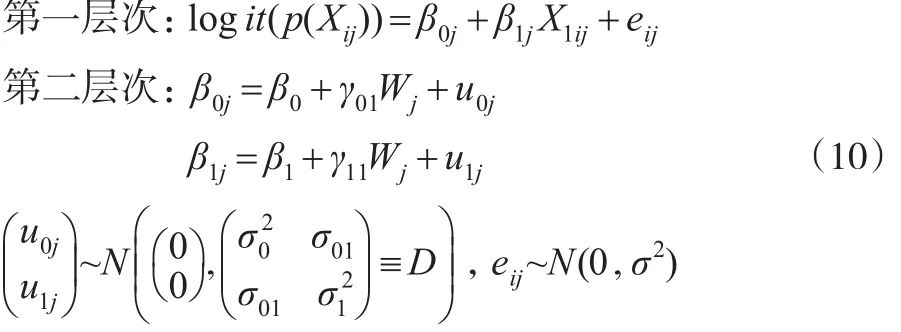
其中γ01为截距方程中预测变量固定的斜率，γ11为斜率方程中预测变量固定的斜率。此模型假定预测变量W对不同群中X1与logit(p(Xij))回归方程的截距和斜率都产生影响。

（7）具有随机斜率与截距且截距斜率其中之一包含第二层次预测变量的倾向得分多层模型。

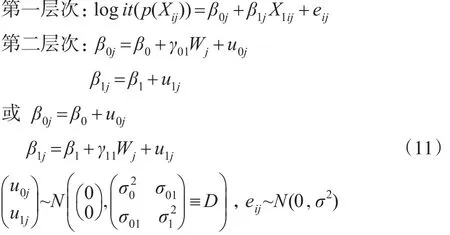
此模型假定预测变量W对不同群中X1与logit(p(Xij))回归方程的截距或斜率产生影响。以上只是考虑了第一层、第二层中一个预测变量的情形，可以根据具体的情况，添加多个预测变量。

在建立倾向得分多层模型之后，可以估计出logit(p(Xij))，得到倾向得分的估计带入式（4）则得到 πij的估计值，即：

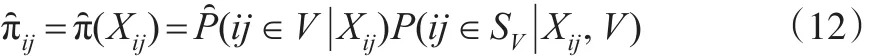
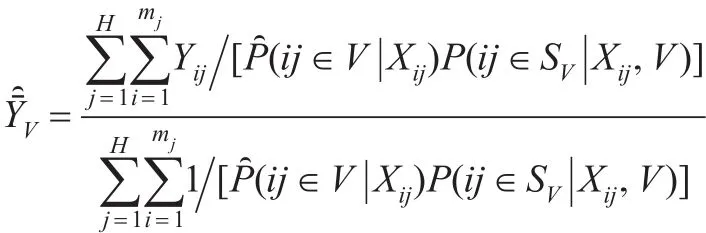
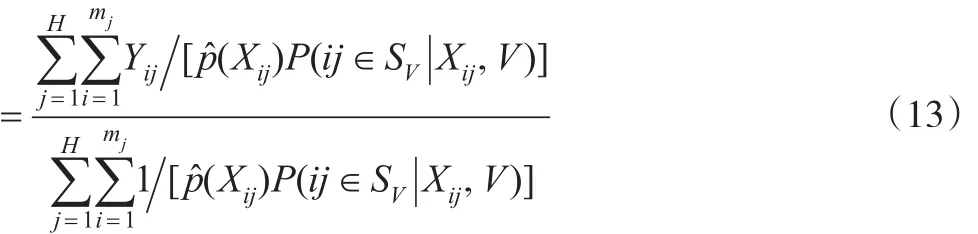
其中网络候选者数据库的调查样本SV可分成H个群（第二层次），第j个群包含mj个个体（第一层次），j=1，…，H。如果总体规模N已知时，可将式（13）的分母换为N。该加权调整方法可称为倾向得分逆加权方法。此外，对总体均值估计的方差可使用重抽样方法，如Bootstrap、Jackknife等来进行估计。

3 模拟研究

现对本文所提出的总体估计方法的效果进行模拟研究。首先生成一个大小为100000（N=100000）的具有嵌套数据结构的有限总体，协变量（预测变量）包括个体层次（第一层次）上服从正态分布N(1，1)的变量X以及群层次（第二层次）上服从正态分布N(0，1)的变量W，群个数m为50，每个群包含的个体单元数都相等为Nm=2000，目标变量Y值由两个协变量X、W以及多层线性模型Y=-0.5+0.5X-0.4W+0.3W×X+u1X+u0+ε来生成，其中u0、u1与ε分别由以下分布来产生：

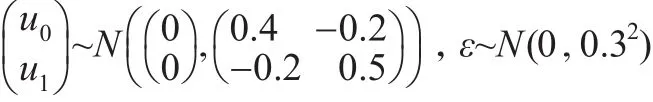
在生成的有限总体中不放回简单随机抽取20个群（每个群2000个单元），然后在每个群中不放回简单随机抽取50个单元，得到样本量为1000（nr=1000）的一个样本，视其为参考样本。然后，从20个群共40000个单元中去掉参考样本单元后的剩余单元中，再分别从20个群中不放回简单随机抽取1000个单元，得到一个有20个群且每个群包含1000个单元的嵌套样本，将其作为网络候选者数据库V，规模为M=20000。接着，采取分层随机抽样从网络候选者数据库V的20个群中不放回简单随机抽取500个单元，作为网络候选者数据库的调查样本SV，样本量为10000（nv=10000）。将上面的过程重复1000次，获得1000组蒙特卡罗样本，针对每一组样本构建具有随机斜率与截距且均包含第二层次预测变量的倾向得分多层模型以及单一层次结构下的Logistic倾向得分模型（忽略数据的嵌套结构）来估计倾向得分，并采用倾向得分逆加权方法来估计总体均值。这里的Logistic倾向得分模型为：

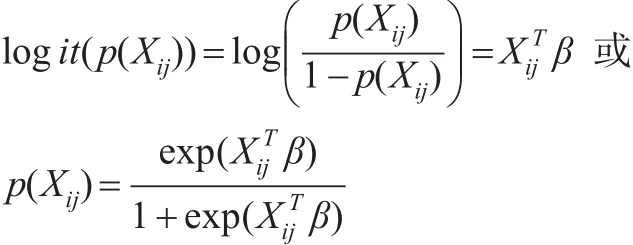
其中Xij=(Xij1，Xij2，…，Xijp)′为协向量，p为协变量个数，β为回归参数。最后，计算1000组模拟样本上总体估计的均值、方差、偏差与均方误差。

表1 基于倾向得分多层模型的总体均值估计的模拟结果

表1为基于倾向得分多层模型和Logistic模型并使用倾向得分逆加权调整方法计算的总体估计的均值、方差、偏差与均方误差。两种方法估计的总体均值较为接近，且总体均值估计的方差基本相同。从偏差上看倾向得分多层模型的逆加权估计偏差相对来说更小，而两种方法估计的总体均值的均方误差一样，说明对于具有嵌套数据结构的网络候选者数据库，基于倾向得分多层模型的总体估计相对于基于倾向得分Logistic模型的总体估计偏差更小，无偏程度更高，而两个估计的效率基本一样。

4 实证分析

实证数据来自2014年美国综合社会调查（General Social Survey，简记为GSS），选取调查中的性别（gender）、年龄（age）、种族（race）、区域（region）、教育（education）、收入（income）和投票变量（vote12）共7个变量，2538个个案的一个数据集，其中区域变量为群的分类变量，共分9个群。因为数据中出现了“不知道（Don't know）”、“无回答（No answer）”、“不适用（Not applicable）”、“不合格（Ineligible）”等选择结果，所以本文将这些结果的个案删除。此外，为了简化计算进一步对变量值进行了一些变换，获得7个变量、191个单元的最终数据集，7个变量的类型与具体取值见表2。

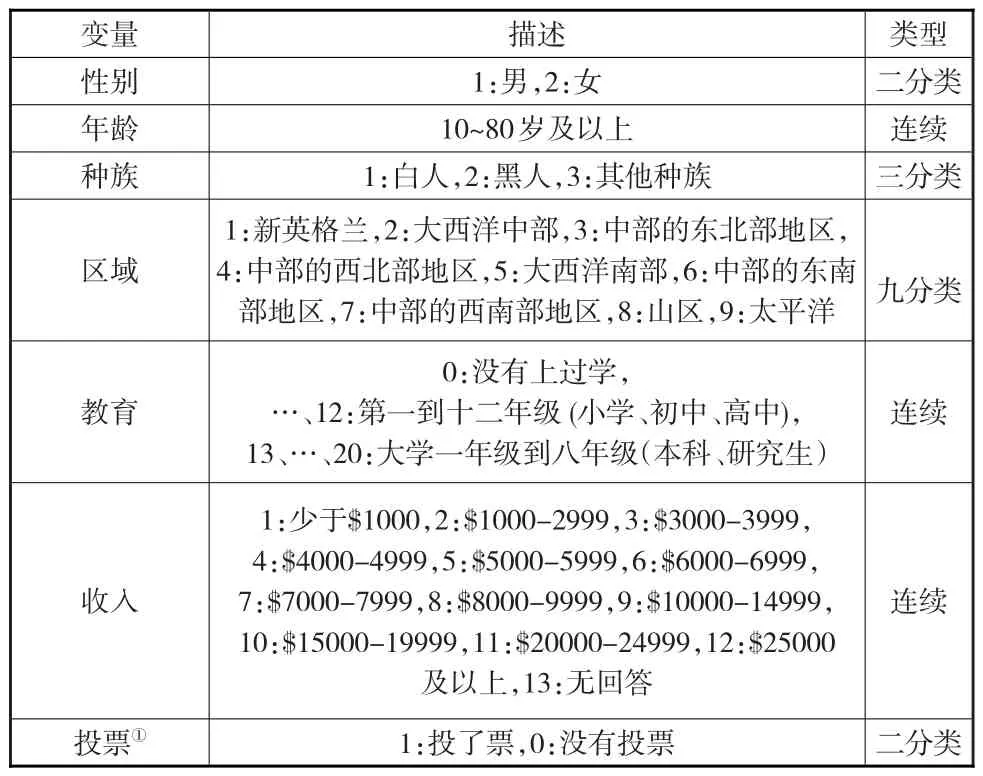
表2 基于倾向得分多层模型推断的实证变量

由于多层模型需要较多的数据，因此本文首先利用Bootstrap来构造一个伪总体。具体地，使用有放回简单随机抽样方法，从191个单元中抽取一个大小为100的样本，重复抽取100次，获得10000个单元，将这10000个单元和191个单元汇总，从而形成一个大小为10191的伪总体（N=10191）。然后，先使用PPS抽样从伪总体中抽取7个群即7个区域，再在每个区域中不放回简单随机抽取20个单元，得到一个大小为140的参考样本（概率样本，nr=140）。接着，从7个区域中去掉参考样本单元之后，再分别从每个区域不放回简单随机抽取300个单元作为网络候选者数据库V（规模为M=2100）。进一步从网络候选者数据库的每个区域中不放回简单随机抽取一个样本量为100的样本，即网络候选者数据库的调查样本SV（nv=700）。在伪总体固定的情况下，重复抽取参考样本和网络候选者数据库的调查样本1000次。

现对2012年总统选举中投票人数所占的比例，即投票变量Yvote的均值进行估计，将年龄、性别、种族、教育、收入作为投票个体（第一层次）上的协变量，并且投票的个体嵌套于区域层次（第二层次）之中。在1000组参考样本与网络候选者数据库的调查样本上，建立具有固定斜率随机截距且不包含第二层次预测变量的倾向得分多层模型以及Logistic倾向得分模型来估计倾向得分，并将倾向得分的逆作为权数进行加权调整来估计投票人数所占的比例。最后，计算1000组样本上总体估计的均值、方差、偏差与均方误差，见表3。

表3 基于倾向得分多层模型的总体均值估计的实证结果

由表3可知，建立倾向得分多层模型与Logistic模型并采用倾向得分逆加权方法计算的总体均值估计的均值都约为0.613，非常接近，并且两种方法估计的总体均值的方差也相差较小。在偏差与均方误差上，倾向得分多层模型逆加权估计的偏差绝对值比倾向得分Logistic模型逆加权估计的偏差绝对值要小，而且倾向得分多层模型逆加权估计的均方误差也较小，表明从偏差和均方误差两个方面来看，对于嵌套结构的数据，倾向得分多层模型逆加权估计不仅无偏程度较高，而且较有效率，估计比较稳健。

5 结论

本文针对网络候选者数据库具有嵌套结构数据的情况，提出建立倾向得分多层模型来估计倾向得分，并利用倾向得分逆加权方法来对非概率样本进行加权调整，从而推断总体。模拟与实证研究表明，对于具有嵌套结构的数据，相对于基于倾向得分Logistic模型的逆加权估计来说，基于倾向得分多层模型的逆加权估计偏差更小，估计的效率更高。可见，倾向得分多层模型比倾向得分Logistic模型更适合具有嵌套结构数据的网络候选者数据库。