单纯形分布联合位置与散度模型的贝叶斯变量选择
赵远英,段星德,庞一成
(1.贵阳学院 数学与信息科学学院,贵阳 550005;2.楚雄师范学院 数学与统计学院,云南 楚雄 675000;3.贵州财经大学 数学与统计学院,贵阳 550025)
0 引言
单纯形(simplex)分布是一类非常重要的统计分布,Barndorff-Nielsen和Jorgensen[1]给出了其最早的分布形式。由于该分布是定义在区间(0,1)上的连续分布函数,在实际应用时是分析百分比数据的有力统计工具,而且在公共卫生、环境和经济等领域都有广泛应用,所以对单纯形回归模型的研究引起众多统计工作者的普遍关注。例如:Song和Tan[2]基于广义估计方程的方法研究了散度参数为常数的单纯形分布广义线性模型;之后Song等[3]基于Song和Tan[2]的方法对可变散度参数单纯形分布广义线性模型进行进一步的研究;Zhang和Wei[4]与Zhao等[5]得到单纯形分布非线性混合效应模型的极大似然估计与贝叶斯估计等。由于均值(位置)结构与方差(散度)结构建模的科学意义,其研究也成为统计研究的热点之一。例如:Smyth[6]获得了可变散度广义线性模型的极大似然估计;基于联合均值(位置)与方差(散度)结构建模的思想,Paula[7]、Lee和Nelder[8]提出了双重广义线性模型的相关统计方法。但是上述文献都未涉及到变量选择问题。经典的贝叶斯变量选择方法有BIC准则[9]、贝叶斯因子[10]和伪贝叶斯因子[11]等。Mitchell和Beauchamp[12]在线性回归模型的框架下提出一种贝叶斯子集选择方法;George和McCulloch[13]基于随机搜寻和Gibbs抽样[14]有效识别潜在的解释变量;Green[15]讨论如何应用可逆跳跃MCMC(马尔科夫链蒙特卡罗)算法来研究模型的不确定性;Nott和Leonte基于Ising模型和Swendsen-Wang算法[16]描述了在广义线性模型框架下的贝叶斯变量选择抽样算法。Leng等[17]利用贝叶斯自适应LASSO方法研究如何选择变量。尽管已经有许多学者研究贝叶斯变量选择方法,也做出了卓有成效的工作。然而,几乎没有文献研究单纯形分布联合位置与散度模型的贝叶斯选择问题。因此,本文的主要目的就是在贝叶斯统计和单纯形分布联合位置与散度模型的框架下,提出一种可行有效的变量选择方法。
1 模型与符号
为了进行贝叶斯变量选择,受Kuo和Mallick[18]思想的启发,本文考虑单纯形分布联合位置与散度模型:
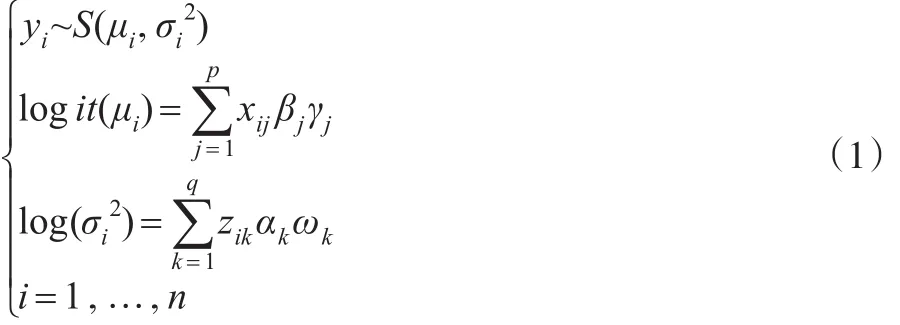
其中,yi~S(μi,)表示响应变量yi服从位置参数为μi∈(0,1)、散度参数为的单纯形分布,其概率密度函数为:
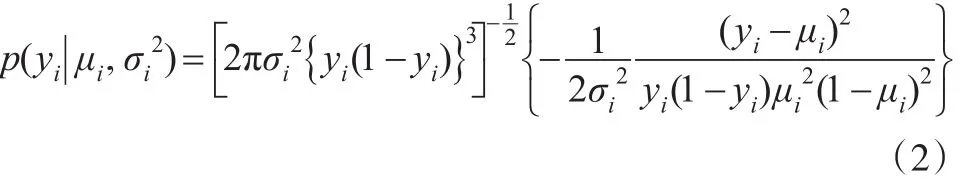
2 贝叶斯变量选择方法
记θ=(βT,αT)T,为了进行贝叶斯统计分析,首先得指定参数θ和示性变量向量γ与ω的先验分布。假设θ,γ与ω的先验分布相关独立,且γj(j=1,2,…,p),ωk(k=1,2,…,q)之间的先验分布也相互独立。即{θ,γ,ω}的先验分布可以表示为:类似于Kuo和Mallick[18]与Zhao等[5],本文考虑参数
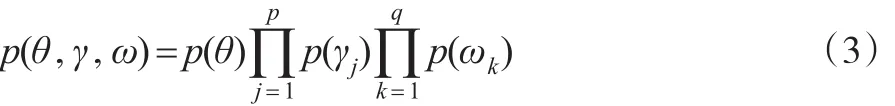
β,α 和 γj(j=1,2,…,p) 与ωk(k=1,2,…,q)的如下先验分布:
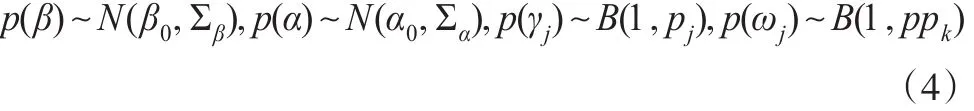
其中N(β0,Σβ)表示均值为β0协方差阵为 Σβ的多元正态分布,B(1,pj)表示参数为1和pj的Bernoulli分布,β0,Σβ,α0,Σα,和pj与ppk是事先给定的超参数。
本文提出一种能同时有效识别位置模型与散度模型中预测变量的贝叶斯变量选择算法。记y=(y1,…,yn)T,x={x1,…,xn}和z={z1,…,zn} 。对参数θ,γ与ω的贝叶斯统计分析可以基于联合后验分布p(θ,γ,ω|y,x,z)∝p(y,x,z|θ,γ,ω)p(θ,γ,ω), 其中p(y,x,z|θ,γ,ω) 是观测数据{y,x,z}的似然函数。因为分层模型的复杂性,很容易发现直接从联合后验分布p(θ,γ,ω|y,x,z)中抽样是不可能的。本文采用近代统计计算工具MCMC方法来解决上述困难。即采用Gibbs抽样[11]方法得到联合后验分布p(θ,γ,ω|y,x,z)的随机样本序列{(θ(t),γ(t),ω(t)):t=1,2,…,T},然后基于此随机序列,通过 γj(j=1,2,…,p)与ωk(k=1,2,…,q)的后验概率来有效识别预测变量xij和zik,最终达到贝叶斯变量选择的目的。从联合后验分布p(θ,γ,ω|y,x,z)中产生的随机样本序列的Gibbs抽样步骤为:(1)选取参数θ,γ与ω的初始值为θ(0),γ(0)和ω(0),并令t=0 ;(2)从条件分布p(θ||y,x,z,γ(t),ω(t))中抽取θ(t+1);(3)从条件分布p(γ||y,x,z,θ(t+1),ω(t))中抽取γ(t+1);(4)从条件分布p(ω||y,x,z,θ(t+1),γ(t+1))中抽取ω(t+1);(5)令t=t+1,重复步骤(2)至步骤(4)直到算法收敛。易知,θ,γ与ω的联合后验分布p(θ,γ,ω|y,x,z)正比于γ,ω), 即:
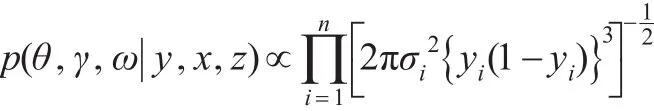
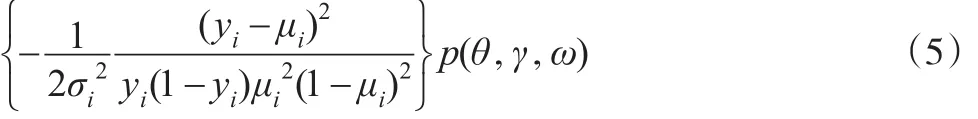
2.1 条件分布
由于θ=(βT,αT)T,本文分别给出β和α的条件分布。
对β的条件分布,由式(3)、式(4)和式(5)有:
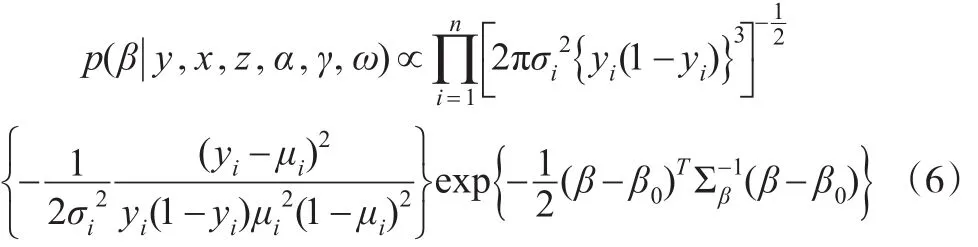
对α的条件分布,由式(3)、式(4)和式(5)有:
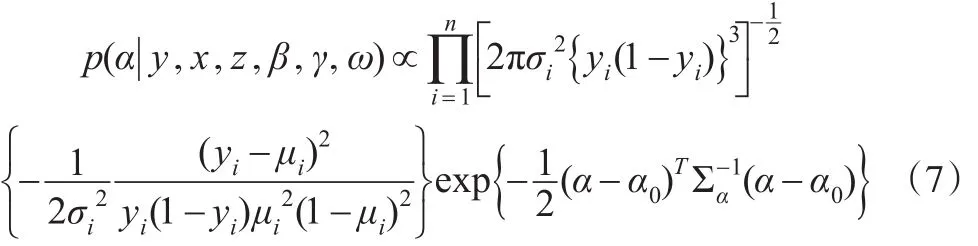
对γ和ω的条件分布,由式(3)、式(4)和式(5)分别有:
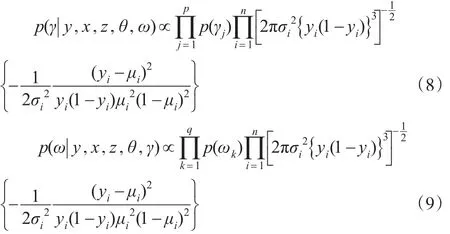
2.2 完成抽样
以下简述如何通过式(6)至式(9)产生所需要的随机样本。首先描述如何通过式(8)和式(9)产生所需要的γ和ω。对任何的j=1,2,…,p,记γ-j为γ删除第j分量之后得到的向量。在给定y,x,z,β,α,γ-j,ω的条件下,可以通过Bernoulli分布向量γ*(γ**)的第j分量等于1(0),其余分量和γ相等;相似地,对任何的k=1,2,…,q,记ω-k为ω删除第k分量之后得到的向量。在给定y,x,z,β,α,γ,ω-k的条件下,也可以通过Bernoulli分布ω**),向量ω*(ω**)的第k分量等于1(0),其余分量和ω相等。
由上面的描述可知,从条件分布式(8)和式(9)中抽样是很容易的。但是式(6)与式(7)中的条件分布并不是常见的标准分布,因此从条件分布式(6)与式(7)中抽样就十分困难和复杂。本文采用Metropolis-Hastings(MH)算法[19,20]来解决这一困难。对于式(6)中条件分布的抽样,本文选取多元正态分布N(0,Ωβ)为建议分布,其中
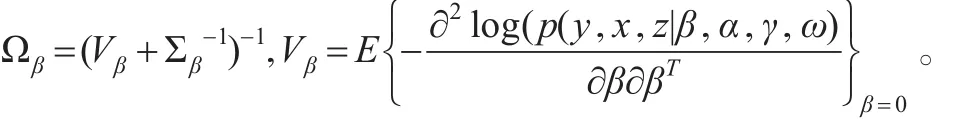
从条件分布中p(β|y,x,z,α,γ,ω)抽β的MH算法的步骤如下:已知β在第t次迭代时的迭代值为β(t),从分布N(β(t),Ωβ)中随机抽取潜在的转移点 β*,并同时独立地从区间[0,1]上的均匀分布U(0,1)中抽取一个随机数u,如令β(t+1)=β(t)。类似地,对于式(7)中条件分布的抽样,选取多元正态分布为建议分布,其中Ωα=(Vα+
从条件分布中p(α|y,x,z,β,γ,ω)抽α的MH算法的步骤如下:已知α在第t次迭代时的迭代值为α(t),从分布N(α(t),Ωα)中随机抽取潜在的转移点 α*,并同时独立地从区间[0,1]上的均匀分布U(0,1)中抽取一个随机数τ,如否则令α(t+1)=α(t)。在具体应用时,通常推荐选取σβ2与σα2使得接受β与α的平均概率为0.25左右。
3 数值例子
假设响应变量yi(i=1,…,n)来自式(1)中定义的单纯形分布联合位置与散度模型,位置参数μi(i=1,…,n)与散度参数σi2(i=1,…,n)分别由下面的模型确定:
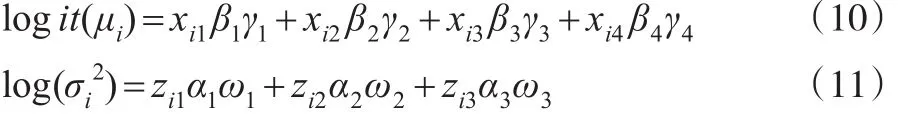
考虑p=4与q=3的变量选择问题,假设预测变量xi=(xi1,xi2,xi3,xi4)T与zi=(zi1,zi2,zi3)T分别独立地从标准正态分布N(0,I4)与N(0,I3)中产生,其中Im表示m×m的单位矩阵。参数的真值被设置为:(β1γ1,β2γ2,β3γ3,β4γ4)T=(0,0,1,1)T, (α1ω1,α2ω2,α3ω3)T=(0,0,1)T。即换言之,式(10)与式(11)分别变为:

因此,式(1)、式(10)和式(11)定义的模型为包含模型不确定性的单纯形分布联合位置与散度模型的类型。在模拟研究时,数据由式(1)、式(12)和式(13)产生,考虑样本量分别为n=50,100和200三种情形,然后应用本文介绍的Gibbs抽样和MH算法进行贝叶斯变量选择分析。表1基于20000次Gibbs抽样给出了出现频率最高的3个模型的比例。由模拟研究的数值结果可以得到以下结论:(1)贝叶斯变量选择方法能同时正确地识别出位置模型中的预测变量为xi3和xi4,散度模型中的预测变量是zi3;(2)随着样本量n的增大,贝叶斯变量选择方法的表现越来越好。
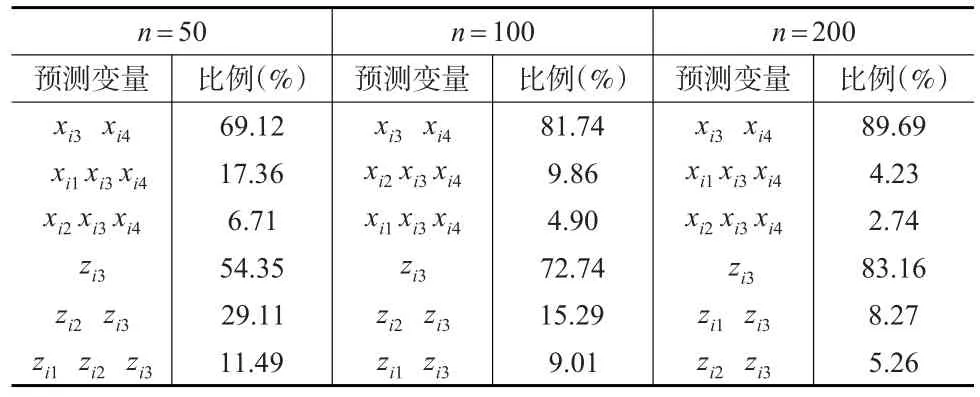
表1 模拟研究的数值结果
4 结论
本文针对单纯形分布联合位置与散度模型,基于Gibbs抽样与MH算法进行贝叶斯变量选择研究。结果表明,所提出来的方法能同时对位置模型与散度模型进行变量选择。模拟研究的结果显示了模型与方法的可行性与有效性。

