微观调查数据抽样权数的可忽略性检验及实证研究

王 峰，米子川

(山西财经大学 统计学院，山西 太原 030006)

一、引 言

在大数据日益成为归纳性统计研究的主流时，以小数据为特征的微观调查数据也再次成为演绎性抽样估计关注的焦点。一般认为，大数据告诉我们“是什么”，小数据则可以告诉我们“为什么”。2018年中国国家统计局与清华大学共同建立了国家统计局-清华大学数据开发中心，对“规模以上工业企业财务状况年度调查”“住户收支调查”等多个微观调查数据和普查数据进行开发应用研究。此外还有诸如中国家庭追踪调查(CFPS)、中国健康与养老追踪调查(CHARLS)、中国综合社会调查(CGSS)以及中国家庭金融调查(CHFS)等等一大批有影响力的微观调查数据。这些众多的微观调查数据，几乎全部是采用复杂抽样方法得到的。在实际的调查中，由于受到调查目的、估计精度、调查费用和可操作性等调查要求的限制，需要采用分层、整群、不等概率和多阶段等多种抽样方法相结合的抽样设计，来提高抽样效率和样本的代表性。我们把除单纯的简单随机抽样方法外，由其他多种抽样方法组合而成的抽样方式称为复杂抽样，由此得到的样本为复杂样本。这里的“复杂”指的是抽样设计的特征偏离了放回简单随机抽样的设计特征，而在有限总体的抽样框中放回简单随机抽样所获得的数据就是独立同分布的数据[1]。显然复杂抽样数据不是独立同分布数据，其入样概率多为不等概率，因此需要引入抽样权数对复杂抽样数据做系列调整。抽样权数中的基础权数，也就是单元入样概率的倒数，可用于调整由于复杂设计带来的不等概率的偏差。更进一步，统计学家在考虑无回答、抽样框覆盖偏差等因素时，需要对抽样权数做进一步调整，形成最终的抽样权数。

很显然，在估计总体均值或比例等一些描述性分析时，抽样权数是避免偏差必不可少的重要因素[2-4]。但是，在研究解释变量和被解释变量关系的模型中是否应该考虑抽样权数，一直存有争议[5-7]。近年来，对于抽样权数和回归模型也有集中性的讨论[8-15]。应用抽样权数的优势是明显的。首先能使样本较好地代表总体，至少在一些重要特征上样本的分布与总体的分布趋于一致，且在一般情况下，加权后的估计量是其总体参数的无偏估计；其次，引入抽样权数可以方便调整样本信息，使样本数据的应用更加灵活。当然，应用抽样权数进行调整也存在明显缺陷：首先增加了估计量的标准误，从而导致估计的不稳定性与精度的降低；其次是抽样权数变化越大，其设计效应(Kishs deff)也越大。因此，在没有必要应用抽样权数的情况下，引入抽样权数可能不仅不会使偏差减少，反而会造成估计量有效性的降低。另一方面，如果在应该加入抽样权数的情况下，没有加入抽样权数，可能会使估计量产生更大偏差。

那么，在什么情况下应该使用抽样权数呢?更进一步，使用复杂调查数据建立解释变量和被解释变量关系模型中是否应该使用抽样权数?Bollen认为大体分三类：一类主要来自生物统计、公共卫生和抽样调查领域的学者，一般使用抽样权数；另一类来自经济社会领域(包括计量经济)的学者，一般不考虑抽样权数；还有一小部分学者可能用也可能不用权数[2]。Chambers和Skinner认为目前还没有一个明确的答案[16]。本文将从抽样权数的低效性和抽样权数影响的显著性入手，在平衡两者得失的基础上，给出一个判断是否使用权数的思路，作为解决上述问题的一个参考，这也是本文的一个创新之处。

二、抽样权数影响的检验

一般地，引入抽样权数的估计量会满足无偏性，但在通常情况下，其方差也会变大。Korn给出了引入抽样权数所带来的方差增大情况的测度指标，即抽样权数低效性的测量，并给出了近似计算公式[17]。但是多数统计学家仍倾向于通过抽样权数对模型造成的影响进行测度，以此来决定抽样权数的取舍。从该测度的方法角度可以分为直接测度(系数差异性的检验)和间接测度(抽样权数辅助检验)。接下来，通过分析抽样权数低效性和抽样权数影响的显著性，在其各自适用性和优缺点的基础上，得到抽样权数可忽略性的检验思路。

(一)抽样权数低效性的测量

(1)

(2)

该公式来源于Korn，这里的CV是样本权数的变异系数。低效性的检验来自如下逻辑：我们当然希望有一个无偏估计量，但是如果因为无偏而造成的方差(均方误差)过大，我们还是选择一个有偏估计量。这个低效性的计算就是测算这个方差(均方误差)大多少，如果没大多少，我们应该选择无偏估计量，即应该使用抽样权数。如果低效性很大了，说明加入权数后造成的方差(均方误差)太大了，我们放弃无偏性，选择有效性，即不应该加入权数。

那么到底方差(均方误差)大多少就是太大了呢？目前还没有一个客观的标准，但是可以从以下几个方面去考虑：

从低效性的绝对程度看：Korn认为，5%到10%的低效性在实际应用中不是很大[17]。本文认为，考虑到当前抽样设计的复杂性，尤其是为降低抽样成本以及无回答因素所带来的抽样设计上的复杂化，不超过30%的低效性，在实际中都会认为不是很大。这一点在本文后续的国内外数据测算中得到验证。

从低效性对估计量期望精度的影响看：例如，在75%的低效性下，使估计2%的标准误从0.01%增加一倍到了0.02%，不会认为是不可接受的大。同样75%的低效性下，使估计2%的标准误从0.5%增加一倍到了1%，这一般会认为大到了无法接受的程度[17]。

从未加权估计量偏差的期望大小来看：如果能够准确估计未加权估计量的偏差，则可以考虑用偏差帮助选择是否加权。即使不能从数据中足够准确地估计出偏差，若能从理论上说明对于某些类型的参数，偏差可能会很小。例如，在估计两个均值或比例的差异时，偏差会比估计单个均值或比例时小。在这些情况下，即期望偏差很小时，一般不会特别反对使用未加权估计量。

总的来看，从抽样权数低效性测量的角度来判断是否应该使用抽样权数，还是需要研究者的主观判断，不同的使用者可能会有不同的结果；另外，在实际的应用中，出于计算方便，一般采用近似计算，在某些情况下可能存在误导(参见例子[17])。但是，低效性测量的优势也是明显的，首先低效性测量不依赖于所采用的推断方法或模型，这样适用性就很强；另外低效性的计算只依赖于抽样权数的分布且计算简单方便。

以上是根据抽样权数对估计量方差(均方误差)的影响，来判断是否使用抽样权数。另外一个思路是通过比较回归模型中加权和未加权的系数是否有显著差异来判断是否需要加权，或者将权数置于模型中判断其是否显著。

(二)抽样权数影响的显著性测量

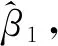
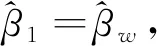
2．抽样权数辅助检验(Weight Association Tests)。Hausman曾建议评估其他形式的方程Y=Xβ+XMβM+ε中βM的显著性来判断设定误差[18]。这里的XM是X的一个合适变形。用F检验H0：βM=0来检验设定误差。另外，与一般多元回归的假定类似，使用F检验需要我们假定ε来自于正态分布。尽管Hausman建议用这样一个形式去检验各种设定误差，但他并没有考虑用它做加权检验。

Dumouchel等利用Hausman的回归方法并将其用于确定是否加权[20-21]。再次考虑方程Y=Xβu+Xwβw+ε，这里Y是被解释变量的向量值，X是未加权的解释变量阵对应的系数为βu，Xw是相同解释变量阵对应的加权系数为βw，ε是误差向量。Dumouchel and Duncan建议用OLS估计这个回归模型然后用F检验H0：βM=0去检验是否需要权数，拒绝原假设意味着需要加权。可以看出尽管Hausman并没有这么做，作为权数辅助检验(WA检验)的Dumouchel和Duncan和Fuller的F检验回归法都是遵循Hausman替代基于回归的设定误差检验。Fuller将这一方法做了一个改变，推荐用回归Y=Xβu+Wα+ε，这里W是权数变量，检验其系数α是否显著非零。

三、抽样权数可忽略性检验的操作路径

在得到调查数据的抽样权数后，其分布就容易直观得到。加之低效性的判断不依赖于所采用的模型方法，因此在判断抽样权数是否可以忽略时，首先计算抽样权数的低效性，并根据前述内容做出低效性是否可以接受的判断。

为给出低效性的一个一般经验水平，这里给出了一些常见分布下的抽样权数频数分布图。样本量取1 000，见图1，从上往下依次为：均匀分布 [U(a=1，b=1 000)] 、正态分布 [N(μ=1 000，σ2=10)] 、二项分布 [B(n=50，p=0.25)] 、指数分布 [e(λ=0.1)] 、卡方分布 [χ2(3)] 、Possion分布 [P(λ=4)]抽样权数的频数分布图。因为这里都是权数所以不是整数的全部取最大整数。

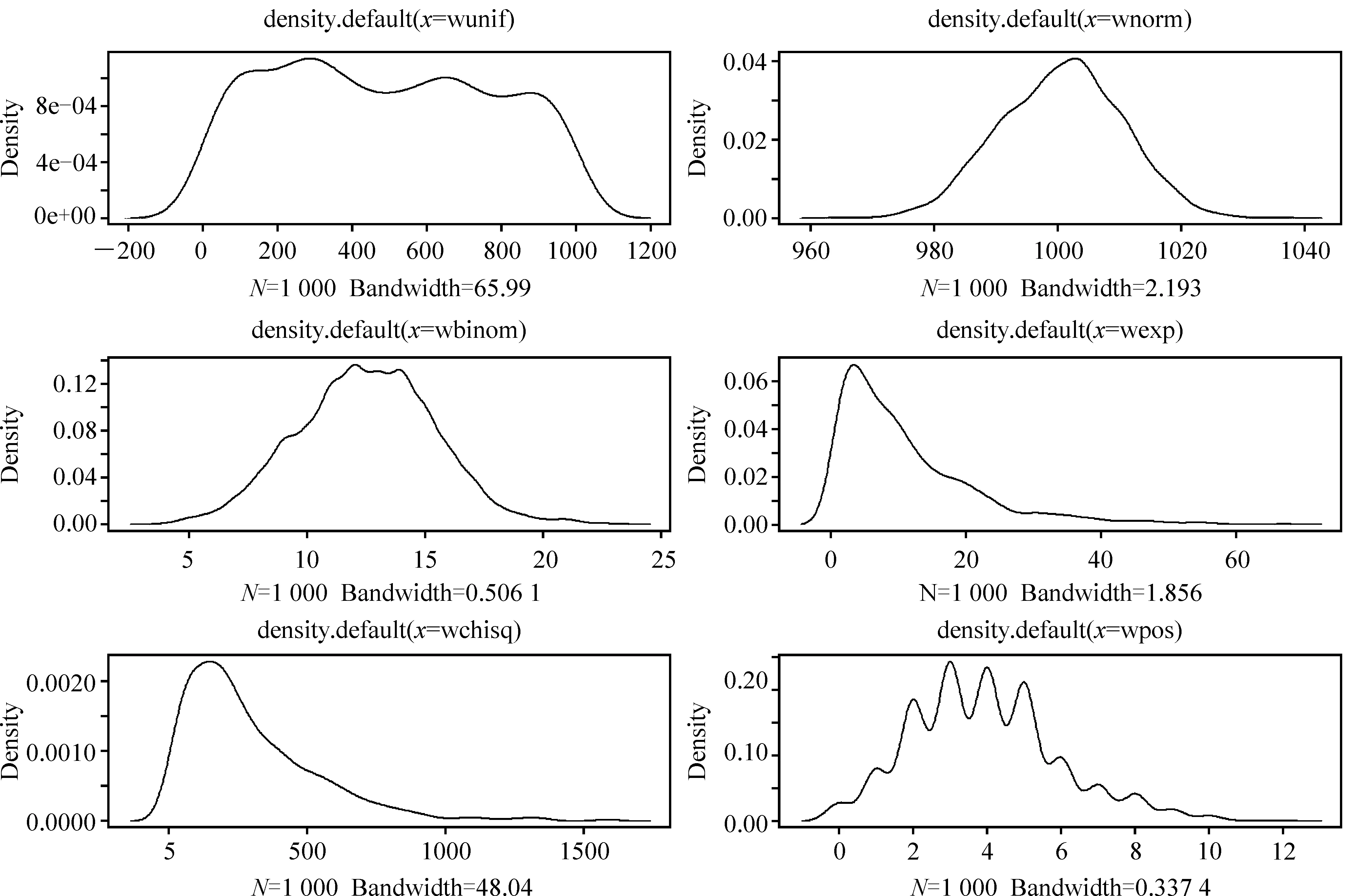
图1常见分布下的权数分布图

考虑到常数分布很简单，为一条水平直线，这里没有画出。对于常数分布，样本权数的低效性显然为零。因为此时的样本就是等概率抽选，也可以认为样本是自加权的，不存在因为权数的引入而造成估计量标准误的增大。因此，抽样权数的低效性为零，公式的计算结果也为零。可以认为，在不考虑抽样权数的调查数据分析时，都是默认抽样权数为常数，这显然可能会低估估计量的标准误，更主要的是通常会失去估计量无偏性。一般情况下，抽样权数的分布不会是常数，除样本是自加权样本外，均会产生抽样权数低效性的发生，这里测算了以上几种常见参数分布的抽样权数的低效性，见表1。

表1 抽样权数在常见分布下的低效性

① 这里需要说明的是“再抽样权数”与抽样权数一样仅仅是一个公布的权数。因为中国家庭追踪调查(CFPS)抽样设计的复杂性，调查数据清理和加权调整也异常复杂，耗时较长，无法满足研究者对调查数据进行快速分析的需求。因此，在中国家庭追踪调查的数据库中包含了一个再整合数据库，即对5个“大省”进行再抽样调整样本，使5个“大省”的抽样比与“小省”的抽样比近似相同，以便在没有及时获得抽样权数的情况下利用再抽样调查权数去推断总体。

以上图形可以从便捷的角度给出实践中抽样权数分布的直观认知。即实际中可以很方便的画出抽样权数的频数分布图，如果这个分布图与上述的某个图形类似，就可以相应的得到抽样权数低效性的一般认知。

由于抽样权数的分布图形只是对抽样权数低效性判断的一般认知，具有很强的主观性，多数情况下甚至是无法做出判断，因此这里综合抽样权数的低效性和抽样权数影响的显著性，提出一个检验抽样权数可忽略性的判断路径，见图2。

当抽样权数的分布为正态分布[N(μ=1 000，σ2= 10) ]、二项分布[B(n= 50，p= 0.25) ]和Possion分布[P(λ=4)]时，抽样权数的低效性比较小，也就是说考虑抽样权数对估计量标准误的影响很小，甚至可以忽略不计，这时候应该使用抽样权数，即在保证估计量无偏的情况下，不会对标准误产生很大影响；如果抽样权数的分布为指数分布[e(λ=0.1)]时，此时的抽样权数无效性达到了44.6%在这种情况下就要格外谨慎，虽然考虑抽样权数能使估计量无偏，但此时估计量的稳健性会较差。通常会选择稳健性，而放弃考虑抽样权数。当然也可以选择重新构建研究的子总体，获取新的抽样权数重新判断； 如果抽样分布类似均匀分布[U(a=1，b=1 000) ]和卡方分布[χ2(3)]时，低效性达到了24.5%和25%，此时考虑抽样权数可能会影响到估计量的标准误，至于影响的大小是否能够接受，可以用上述假设检验的方法去检验。但为什么不直接用该假设检验来判断呢？原因有二：一是低效性的判断方便快捷不依赖于所采用的方法；二是假设检验的判断，目前还局限于回归模型的分析中，虽然对其他模型的构建可以提供参考，但当前还没有证明该假设检验可以应用于其他一切模型。

图2 抽样权数可忽略性的判断路径图

四、实证研究

CFPS是北京大学中国社会科学调查中心主持的追踪调查项目之一，调查对象是中国的25个省市自治区的家庭户和家庭户中的所有满足调查条件的家庭成员。在抽样设计上采用三阶段、不等概率的整群抽样设计[22]。本文以CFPS2010的数据为例，来说明抽样权数可忽略性检验。

(一)低效性检验

首先利用抽样权数的分布图做一个直观的分析，图3中左侧图形为中国家庭抽样权数分布图右侧为中国家庭再抽样权数①分布图。这两个图形都与常数分布差的很远，与图1中正态分布[N(μ=1 000，σ2=10)]、二项分布[B(n=50，p=0.25)]相差也比较大，与卡方分布[χ2(3)]类似，因此其低效性都不会很小。对比两个图形，再抽样权数的低效性要大于抽样权数低效性。

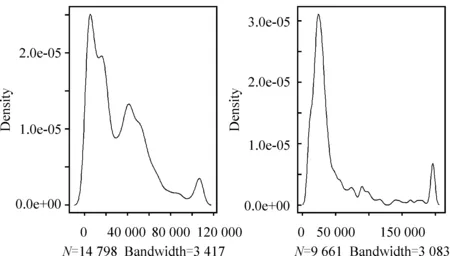
图3 全国家庭抽样和再抽样权数分布图

这里根据式(2)，对CFPS2010的抽样调查数据中的家庭权数和家庭再抽样权数的低效性做进一步分类测算，结果见表2。可以看出中国家庭的抽样权数的低效性为26.208%；其中城镇家庭抽样权数的低效性低于全国水平为25.422%；农村家庭抽样权数的低效性高于全国水平为26.627%。同时也可以看出，家庭再抽样的权数低效性较高，全国、城镇和农村家庭的再抽样权数低效性分别为34.537%、34.676%和33.702%。无论是抽样权数还是再抽样的权数，低效性虽然不小，但也没有大到无法接受的程度。根据笔者掌握的国外抽样权数低效性的测算结果：美国国家健康和营养调查(NHANES)中，NHANESII中2～18岁男孩抽样权数的低效性是34%；NHANESI中25～74岁女性抽样权数的低效性是48%；美国国民健康访问调查(NHIS1987)18岁以上男性的抽样权数的低效性是22%。为便于与国外比较，我们也计算了CFPS2010中25～74岁女性抽样权数的低效性是26.451%，18岁以上男性的抽样权数的低效性是26.131%，前者比美国同一指标低，后者略高。

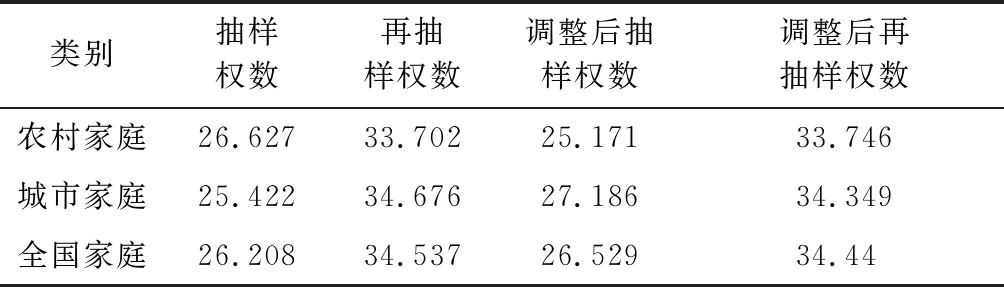
表2 农村、城镇及全国家庭抽样权数的低效性单位：%

① 对于缺失数据可以考虑多种方法去插补，由于这些缺失值对权数的分布影响不大，因此本文直接删除处理；对于家庭消费小于100元的家庭，CFPS用户手册中说明对其做过插补处理，但数据中仍然有6个家庭的消费小于100元，这里也删除处理。

为了做进一步检验，我们计算了家庭消费和家庭收入调整后的抽样权数的低效性。这里面的调整主要包括删除了家庭消费和家庭收入中的缺失数据，也删除了家庭消费在100元以下的数据①。经过这样的调整，抽样权数略微有些变化，见表2。调整后城镇家庭抽样权数的低效性均高于农村家庭抽样权数的低效性，但低效性的变化都不是很大。

接下来我们测算了不同规模家庭的抽样权数的低效性。根据家庭成员数将家庭规模划分为：家1为1位家庭成员、家2为2位家庭成员，以此得到家6及以上为家庭成员数为6位及以上。从表3可以看出，虽然不同家庭规模的样本量差异较大，一位家庭成员的家庭样本数为728，三位家庭成员的家庭样本数为33 556，但它们的抽样权数的低效性都不是非常大，都没有超过30%。

表3 按家庭人口数划分的抽样权数的低效性

因此，无论是家庭抽样权数还是成人抽样权数，以及不同规模家庭的抽样权数，低效性都不是特别的大。因此，我们在使用调查数据时，应该考虑抽样权数，这样既可以得到一个无偏估计量，同时其有效性也不会降低很多。

(二)抽样权数影响的显著性水平检验

由前面的分析可知，在考虑家庭收入和消费时，由于删除了缺失数据和家庭消费小于100元的数据后，抽样权数的分布有了略微的变化。但抽样权数的低效性依然不是很大，因此从低效性的角度看，我们应该考虑抽样权数。为对上述思路与路径做完整的分析，接下来从抽样权数影响的显著性水平来检验抽样权数是否可以忽略。即假设认为抽样权数低效性的大小无法判断，则通过假设检验来判断。

这里利用权数辅助检验的方法，选取Dumouchel和Duncan所述方法对上述数据的抽样权数是否应该引入模型进行检验。Dumouchel和Duncan是将权数及权数与解释变量的交互作用引入模型，利用F检验其系数是否全部为零来判断抽样权数是否可以忽略。因为权数辅助检验需要依据模型来检验，由前述数据，这里对家庭消费和支出建立线性模型来检验抽样权数的可忽略性。

表4 家庭支出关于家庭收入的线性模型比较

注：***表示在1%水平上显著。

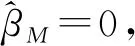
为全面展示抽样权数可忽略性的判断路径图，这里给出了另外一种情况，即抽样权数是可忽略的。依然以CFPS2010的数据为例，选取cyear指标为抽样权数。这其实相当于认为CFPS2010的数据是等概率抽选的，这也是在实际中，微观调查数据建模时经常默认的，即数据是等概率抽样获取的，因此抽样权数可以忽略。利用Dumouchel和Duncan所建议的检验方法，计算得到F(2，8 188) = 1.411，P=0.244，在0.1的显著性水平下，我们不能拒绝，由此得出cyear作为权数是可忽略的。

然而事实是这些数据并不是等概率获取的，所以说，在给微观调查数据建模的时候，如果对抽样权数视而不见，其所建立的模型就值得怀疑，因为多数大型、规范的调查数据很少是等概率抽取样本，同时还要考虑因为无回答和抽样框覆盖偏差等因素所带来的“过抽样”和“欠抽样”等问题。当然不是说对于这类调查数据就必须在模型中考虑抽样权数，如果因为引入权数带来方差的增大，足以影响到数据分析，或者假设检验没有被拒绝，这时候可以如图2所示，返回重新选择研究的数据或者选择不考虑抽样权数处理。但无论怎么样，对抽样权数总归要有一个处理，用要有用的理由，不用也要有个说明，这是我们的写作动机之一，本文就此给出了解决该问题的一个路径。

五、结论与建议

权数是把双刃剑，在提高精度的同时，有可能提高估计量的误差[15，23]。因此，在使用微观调查数据时，是否使用抽样权数，本文给出了一个判断思路。即从抽样权数的低效性和抽样权数影响的显著性两方面入手，给出了一个判断路径图。第一，通过分析抽样权数低效性的计算过程，得出了抽样权数低效性判断的优缺点，并给出了抽样权数在几种常见分布下，低效性的一个一般经验判断。第二，通过对抽样权数影响的显著性检验方法的综述，根据方法的不同，分为系数差异性检验和权数辅助检验，并得出这些检验与Hausman的模型设定误差检验的关系。最后，通过CFPS2010验证了本文提出的检验路径，并给出了CFPS2010家庭抽样调查数据抽样权数的低效性，与国外类似调查数据的低效性进行了比较。通过低效性判断和Dumouchel-Duncan检验说明其抽样权数的不可忽略性，即得到在使用CFPS2010家庭抽样调查数据做统计推断或数据建模时，应当考虑抽样权数。当然，本文所运用的抽样权数影响的显著性检验还局限于回归分析，如何将其推广到其他模型，比如结构方程模型中，还需要做进一步研究；文中抽样权数低效性大小的判断，还缺乏客观统一的标准，需要更多经验数据的积累和方法的创新。