基于EMD-PSO-LSSVR的物料需求组合预测模型

白朝阳，宋林杰，李晓琳

（大连理工大学 管理与经济学部，辽宁大连116024）

0 引言

物料需求预测受到企业内外部多方因素影响，如订单变化、生产能力改变、产品周期化迭代等因素，往往呈现出样本量小且变化周期快、范围大的特点，从而使得需求预测问题难度较高。对于传统预测模型，需要事先知道影响因素的模式,而这种模式主要靠主观分析和特征判别,因此传统模型对于物料需求的预测效果并不理想。

物料需求呈现出非平稳、非线性的时间序列特征。本文拟将EMD和LSSVR的组合进行物料需求预测。运用EMD方法将非平稳时间序列分解为一系列的本征模函数（imf）和一个残差项（res），挖掘出更多的信息，再使用LSSVR模型并结合PSO进行组合预测。并根据某清分机生产企业实际物料需求数据，验证了该组合预测模型的可行性和有效性。

1 EMD-LSSVR组合预测模型

1.1 经验模态分解EMD

EMD通过数据的特征时间尺度来获得本征波动模式，将复杂时间序列分解为能够直接分析的有限个本征模函数以及残差。因其在处理非平稳、非线性数据上的优越性，该方法可以应用于任何类型的时间序列（信号）的分解，且比之前的处理方法更具有明显的优势。EMD方法的分解步骤如下：

（1）确定数据序列x(t)的局部极值。找出当前序列的所有局部极大值点，使用三次样条函数拟合形成当前数据序列的上包络线U(t)。同样，找出数据序列所有局部极小值点，形成数据序列下包落线L(t)。计算上包络线和下

然后将m1(t)从原始序列x(t)中除去，形成新的序列h11(t),若其满足对称性，且局部极大值均为正数，所有局部极小值均为负数，则所得到的分量h1(t)为IMF否则，用h11(t)替代x(t)并重复上述过程，直到找到满足要求的IMF，具体公式为：

（2）满足要求的时间序列h1n(t)即为IMF1，并定义为c1(t)，用原始序列x(t)减去c1(t)即可得到r1(t)为：

（3）将r1(t)作为原始序列，并重复上述步骤直到rn(t)无法再分解。最终原始时间序列被分解为：包络线的平均值m1(t)：

其中，x(t)表示数据的原始时间序列，ci(t)表示每个IMF值，n为IMF函数的个数，r(t)表示残差。使用EMD需要满足以下假设条件：

（1）数据至少有一个最大值和一个最小值；

（2）数据的局部时域特性由极值点间的时间尺度唯一确定；

（3）如果数据没有极值点但有拐点，则可以通过对数据进行一次或多次微分求得极值，然后再通过积分来获得分解结果。

物料需求时间序列都符合这些假设，因此可以用EMD方法分解。

1.2 最小二乘支持向量回归LSSVR

在给定样本空间集中，S={(xi，yi)|xi∈Rn，yi∈R，i=1，…，N}，xi为函数的输入值,通过非线性映射生成高纬度空间函数的对应值，即函数的输出值yi，其优化问题为：

其中，C为惩罚系数，φ(xi)为非线性映射函数，ei为误差项，i表示误差项个数。未解决该优化问题，引入拉格朗日函数：

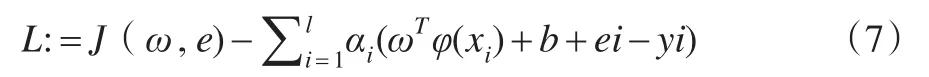
根据Karush-Kuhn-Tucker条件，求解得：

分别对w、b、ei、αi求偏导，然后消除ei和w后,式（8）转变为：

求解得：

其中，ψ(x，xi)为内核函数，本文选取拟合精度较高且适用于小样本的高斯函数为核函数：

式（11）中，σ为高斯核函数的宽度参数，它隐含地定义了从需求函数特性输入空间到高维特征空间的非线性映射，从而控制最终解的复杂性。

1.3 EMD-PSO-LSSVR组合预测模型构建

第一阶段，首先针对不同类型参数，将原始物料需求数据进行经验模态分解，得到若干IMF和一个残差趋势项Res。然后使用通过选取平均值、标准差、偏度、均方值、相关系数等统计指标进行聚类分析，把IMF聚为高频、低频两类，并迭加相同类别的IMF。得到高频聚类本征模态函数CIMF1（Comprehensive Intrinsic Mode Functions 1)和低频聚类本征模态函数CIMF2（Comprehensive Intrinsic Mode Functions 2)。最后以CIMF1、CIMF2和Res作为训练样本，建立LSSVR进行预测。

第二阶段，输入上述步骤得到的训练样本训练LSSVR，获得最优参数，从而获得物料需求预测结果。考虑到最小二乘支持相量回归预测模型的关键问题在于参数的确定，本文采用PSO算法来优化LSSVR的物料需求预测型，具体步骤如图1所示。

图1 PSO算法优化LSSVR参数过程

2 物料需求的EMD-PSO-LSSVR组合预测

2.1 数据来源及研究方法

本文选取2012年1月至2015年3月，A金融设备制造企业MES（Manufacturing Execution System）系统中某清分机产品族通用材料S的月出库数据作为研究样本。由于该行业物料需求同时受订单驱动以及上期期末库存量的影响，因而数据序列会呈现出周期性。为评价组合预测模型的性能，本文选取平均绝对误差MAE（Mean Absolute Error）、平均绝对百分比误差MAPE(Mean Absolute Percentage Error)、均方根误差RMSE(Root Mean Absolute Error)为误差评价指标，与ARIMA、三次指数平滑以及LSSVR预测模型进行对比，从而说明EMD-PSO-LSSVR组合预测模型在物料需求预测应用上的有效性。评价指标计算方法如式（12）、式（13）、式（14）所示,其中pi、xi分别为物料需求在时间点i时的预测值与实际值：

2.2 数据背景及描述性统计

A企业是MTS（Make-to-order）-ATO(Assemble-to-order)的混合型生产模式,同时该企业于2012年实行产品族管理战略。针对产品族内的通用材料S，企业会提前进行生产决策以避免采购、生产周期过长而导致的拖期违约等问题。在接到具体订单后，生产部门会根据订单要求制定当期装配计划以满足产品订单需求。通用材料S是某类型清分机产品族内所使用的特殊材料，而该类型清分机市场订单不稳定，在2012—2015年中通用材料S的需求量时常会有大幅度的波动，使用传统预测模型难以预测。关于物料需求数据的具体统计特征指标如表1所示。

表1 物料需求数据统计特征指标

2.3 EMD及合成分析

2.3.1 EMD分解结果

根据EMD算法，越早分解出的IMF频率越高，波动性越大，越能代表原始序列在近期所表现出的特点，而分解最后剩余的残差项则代表了原始序列的发展趋势。物料需求序列使用EMD分解后，得到3个IMF分量和1个残差项，分解结果如图2所示。其中，按照频率从高到低排列分别为IMF1、IMF2、IMF3，IMFs分量曲线均呈现出一种围绕零均值线、局部最大值、和局部最小值基本对称的振荡形式。而且可以发现，随着频率的降低，序列的规律性越来越明显。

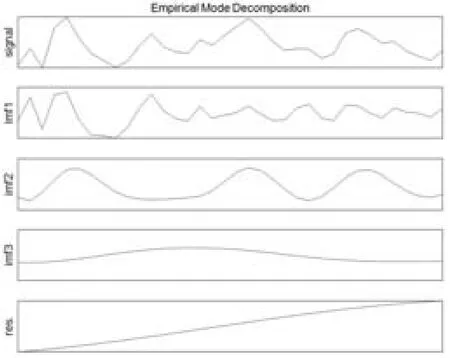
图2 EMD分解结果

2.3.2 EMD聚类合成结果分析

表2是IMFs以及RES的特征统计指标，可以看出最大值与最小值的范围差距在不断缩小，选取描述统计结果中能够体现序列特征的平均值、标准差、峰度、偏度、相关系数等指标并结合IMF的波动频率进行聚类分析。

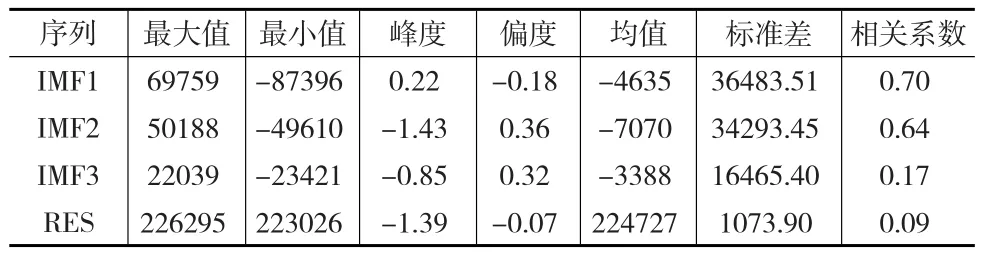
表2 EMD分解结果描述统计

从表2中还可以看出IMF1及IMF2波动频率较高，数据的离散程度也较为接近且与原时间序列数据的相关性较强，因此将IMF1及IMF2叠加构成CIMF1，即高频聚类本征模函数；同时IMF3成为CIMF2，即低频聚类本征模函数，分解聚类后的波动趋势显示：聚类后得到的CIMF1、CIMF2及残差项对于原始时间序列均有隐含的统计学解释，能够说明其波动原因及长期趋势。CIMF1反映的是原始物料需求的序列短期内的波动，由于产品族管理战略的施行，A企业针对通用材料S的计划调度管理也愈加成熟，通过预先生产策略减轻产品需求波动对通用材料需求数量波动的影响。CIMF2的波动反映出事件对于物料需求序列的影响，其振幅体现的是事件对于物料需求的影响程度而周期则表示外界影响的周期长短。最后看到残差项的趋势是长期上升但趋于平缓，反映出物料需求的长期趋势是微弱上升的，这与产品族所处市场已趋于饱和的情景是相符合的。

2.3.3 面向高频聚类本征模函数的LSSVR参数优化

本文取粒子群算法的加速度因子C1和C2取经验值C1=1.5，C2=1.7，种群规模设为20，初始种群随机生成，搜索终止条件为达到最大迭代次数100，惯性权重Wmax=0.8，Wmin=0.3，参数自动寻优得到最优正则化参数C=2.5354，最优核函数参数σ=0.5457,相关系数r=99.84%具体拟合寻优结果如图3、图4所示。

图3 LSSVR拟合结果曲线

图4 PSO适应度迭代曲线

从以上处理结果来看，粒子群优化后的组合预测模型拟合效果良好，同时收敛速度快。从长期趋势看，物料的需求量成略微上升的趋势，并且随着时间的增长，物料需求量的震荡幅度逐渐减弱，这也符合企业物料管理水平逐渐成熟的客观实际。

2.3.4 面向低频本征模函数的函数拟合

根据低频CIMF2的形态构造函数表示数据趋势，CIMF2的形态和Gumbel概率密度函数的形态相似。本文使用origin软件的函数拟合功能对CIMF2使用高斯拟合，得到拟合结果及残差值，非线性拟合确定系数R2的值为0.9873，说明拟合结果良好，具体函数拟合式为:

通过对CIMF2进行拟合,得到最优参数如表3所示，其中y0为常数项，xc为尖峰中心的坐标值，w为峰宽，A为曲线尖峰的高度。

表3 CIMF2拟合参数

2.4 模型评价与对比

目标时间序列共有39个观测值，本文选取前36个点作为回归训练样本集，后3个点作为预测测试集，将EMD-PSO-LSSVR模型与三次指数平滑、ARIMA、LSSVR模型进行回归预测对比分析，以验证EMD-PSO-LSSVR组合预测模型在物料需求预测问题中的有效性，预测结果如表4所示。

表4 预测结果分析

表4给出四种模型的预测结果和相对预测误差。EMD-PSO-LSSVR模型的预测精度优于其他三种模型，预测出的S物料需求值较其他三种模型更接近于实际值。组合预测模型预测期内的最大、最小相对预测误差为2.15%和5.01%，其他三种模型的最大、最小相对预测误差较大，分别为6.89%和9.97%、4.35%和13.57%、3.99%和6.33%。

为了评价模型的预测效果，本文选取了MAE、RMSE以及MAPE三种指标，用于评价不同方法对测试样本的预测能力。MAE、RMSE均是用来衡量的是预测值与实际值之间的偏差，其中MAE是常用的评价指标，其特点在于预测结果的个体差异对于平均值的权重相同，而RMSE对于预测结果中偏移程度大的误差比较敏感，更能体现预测结果的精准度。MAPE用来衡量误差与实际值之间的比例，真实反映了预测结果偏移的程度。经过计算，得到误差分析结果如表5所示。

表5 预测误差分析结果

从表5可以发现：EMD-PSO-LSSVR组合预测模型的MAE、RSME和MAPE均小于三次指数平滑模型、LSSVR模型以及ARIMA模型。这说明对于样本量小且变化模式复杂的物料需求预测问题，EMD-PSO-LSSVR组合预测模型能够比常用的三次指数平滑模型及ARIMA模型提供精度更高、更加可靠的预测结果。另外，从各个指标来看，组合预测模型相较于LSSVR模型平均提高了接近3倍的精度，这是经过EMD分解合成将非平稳的数据变得具有一定的规律性，从中可以挖掘出有效的信息，从而提高了预测精度。

EMD-PSO-LSSVR组合预测模型与三次指数平滑模型预测结果的趋势与实际值相同，而ARIMA模型以及LSSVR模型则呈现出了相反的趋势。为了实现精益化管理，提升运营效率，企业需要通过分析未来物料需求的发展倾向，来制定更加合理的生产计划。而趋势预测结果的偏差会给企业生产管理者提供错误的决策信息，使其对未来物料需求的走势产生错误认知，从而造成过量采购或物料短缺等问题，最终会对企业经营造成负面影响。

3 结论

本文基于最小二乘支持向量机技术对非平稳时间序列数据进行预测，为降低数据非平稳性对预测结果的影响，利用经验模态分解（EMD）将原始序列分解为若干IMF分量和残差趋势项，根据IMF分量的描述统计结果，根据其频率的高低将其聚类为高频和低频两部分。利用高频的部分来预测物料需求的短期波动，利用低频部分来预测物料需求的长期趋势，并利用粒子群算法（PSO）对模型参数进行优化，最后将高频、低频以及残差项汇总，得到最终预测结果。为了验证EMD-PSO-LSSVR组合预测模型的有效性，本文选取了A公司的通用材料S的需求量为研究对象，并对比分析了ARIMA、三次指数平滑、LSSVR三种模型的拟合和预测效果。结果表明，EMD分解后，利用LSSVR做物料需求量回归预测的拟合效果最优，验证了EMD-PSO-LSSVR组合预测的有效性，能为企业做物料需求预测提供参考。