基于供应可靠性的供应链契约设计

李新军，刘兴华

（烟台大学 经济管理学院，山东 烟台 264005）

0 引言

信息不对称渗透在社会生活的方方面面，在一个两级供应链生产系统中，制造商和供应商之间存在的不对称信息如：制造商生产成本、市场需求、供应商可靠性等。而要实现私有信息共享也面临着诸多难题：一方面，供应商分享私有信息并不一定有利于其利润的增加，公开信息动力不足；另一方面，供应商提供的私有信息并不完全可信，信息共享需要在供应链之间建立庞大的信息系统，共享信息耗时费力。本文主要研究信息不对称情况下制造商如何建立有效的甄别机制以区分不同类型的供应商。

二级供应链中，制造商面临着供应商的中断风险，同时要考虑固定支付、变动支付、订货量和惩罚成本四个变量作为采购决策的要素。本文运用委托代理理论和甄别博弈理论，建立两阶段动态规划博弈，并探究获取供应商可靠性信息的价值。

1 模型假设与符号说明

供应商由于遭受随机中断，如恶劣天气、火灾等导致的存货不合格，柔性制造导致的零件不配套，运输过程中发生事故等，且一旦发生中断，则交付量为0，即完全中断。供应商包含两种供应类型：高可靠性（H）和低可靠性（L）（可靠性表示供应商能够成功交付产品的概率），t∈{H，L}。由于可靠性信息为私有信息，可通过海萨尼转换将其转换为风险条件下的选择，从而将不完全信息博弈转换为完全但不完美信息博弈。通过此转换，尽管供应商的可靠性类型无法确定，但可知道供应商为高可靠性和低可靠性的概率分别为αH和αL，且αH+αL=1。ρt表示t类型供应商的交付状态（交付过程是否发生中断），θt表示供应可靠性水平，即供应商成功交付产品的概率。ρt与θt之间的关系为：

定义θH=h，θL=l，且h＞l，即高可靠性供应商比低可靠性供应商成功交付产品的概率高。ct表示t类型供应商完全可靠即不发生中断情况下的单位生产成本，若考虑到中断风险则供应商的实际生产成本为且即低可靠性供应商成功交付单位产品的平均生产成本大于高可靠性供应商成功交付单位产品的平均生产成本。

K表示制造商的订货成本，此成本对两个供应商无差异。r表示制造商对产成品的单位售价，且D表示市场需求，f(x)和F(x)分别表示其密度函数和分布函数。

契约设计如下页图1所示。契约形式为(X，q，v，p)，其中X表示制造商的固定成本，q表示制造商的订货量，v表示制造商的单位变动成本（为保证成功交付产品时X≥0，则必有v≤ct），p表示制造商的单位缺货成本。制造商向供应商提供一组可靠性不同的契约菜单，运用激励相容机制，由供应商做出选择，向制造商表露其真实的可靠性类型。

图1 契约签订和执行过程

2 模型构建与分析

若z＞q，不论产品是否成功交付，其收入和z=q时的收入相同，但生产成本显然高于z=q时的生产成本，因此z≤q。整理后得供应商期望利润为：

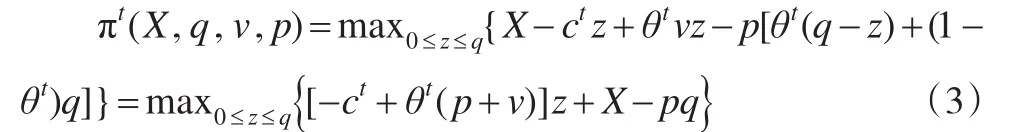
2.1 供应商生产决策

在第二阶段的执行过程中，契约(X，q，v，p)既定条件下，t类型（t∈{H，L}）的供应商为达到利润最大化的目标，将根据契约内容决定自己的产量z。由于交付过程可能发生中断，因此最终交付量为min(q，ρtz)，其中q表示订货量，交货后供应商接受变动支付vmin(q，ρtz)及惩罚成本p(q-ρtz)+（符号“+”定义为：当x＞0时，x+=x；当x≤0时，x+=0）。供应商的期望利润为：

求导可知供应商的最优产量z与X无关，而只与q、p、v相关，因此用zt(q，p，v)表示t类型供应商的最优产量。考察z的系数，得出定理1。

定理 1：给定契约 (X，q，v，p)，供应商的最优产量zt(q，v，p)和期望利润 πt(X，q，v，p)，如表1所示。

表1 供应商最优产量及期望利润

由表1中最后一列可得，供应商的期望利润随其可靠性的增大而增加，即供应商越可靠，则其成功交付单位产品的平均生产成本就越低，也就意味着期望利润越高。

定理2：对于契约 (X，q，v，p)，相比于低可靠性供应商，高可靠性供应商具有可靠性优势τ(q，v，p)=πH(X，q，v，p)-πL(X，q，v，p)，如表2所示。

表2 高可靠性供应商相对于低可靠性供应商的可靠性优势

因为X在运算中抵消了，所以τ不是X的函数。

从表2可以看出，两种类型供应商的可靠性之差越大，则对高可靠性供应商越有利，故高可靠性供应商为了获取更多利润有动机伪装成低可靠性者。而制造商为了获得供应商真实的可靠性类型，可以运用激励相容机制，针对不同类型的供应商设计不同的契约，引导供应商暴露自己的真实类型。

2.2 制造商契约设计

分析签约阶段制造商的契约设计问题。制造商提供一组使自己利润最大化的契约菜单，供应商从菜单中选择一个契约 (Xt，qt，vt，pt)，决定最优产量zt(qt，vt，pt)，并获得最优利润 πt(Xt，qt，vt，pt)，同时向制造商暴露自己的可靠性类型。制造商获得利润为产品的销售收入和供应商缺货的罚金之和减去固定支付和变动支付。

制造商设计的契约菜单不但要最大化自己的期望利润，还要使供应商真实暴露自己的可靠性类型。契约满足：

其中，qt≥0，vt≥0，pt≥0，t∈{H，L}。

式（5）和式（6）分别为激励相容约束，诱导供应商暴露其真实的可靠性类型；式（7）和式（8）分别表示个体理性约束。同一契约条件下，高可靠性供应商获得更高利润，即XL-cHqL+hvLqL-(1-h)pLqL≥XL-cLqL+lvLqL-(1-l)pLqL，结合式（5）和式（8），可知式（7）必定为松约束，故删掉。以上模型描述的是一个完美贝叶斯均衡问题，下面从完全信息和可靠性信息不对称两个角度分别进行分析。

2.3 完全信息下制造商契约设计

完全信息下，没有必要考虑激励相容约束，故删除式（5）和式（6）。两种类型的供应商均得到能够接受其最低的保留利润，即 πH(XH，qH，vH，pH)=πL(XL，qL，vL，pL)=0 ，代入式（4）中，得制造商的期望利润为：

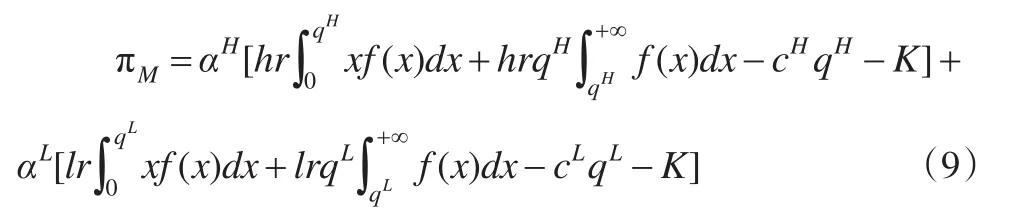
式（9）自动分离为两种类型供应商各自的非线性规划问题。定理3给出了制造商在供应可靠性信息对称时的最优契约设计。

定理3：当获知供应商的可靠性类型为高可靠性H或者低可靠性L 时，制造商设计的最优契约（xt，qt，vt，pt）中各决策变量值，如下页表3所示。

表3 信息对称下制造商的最优契约设计

2.4 可靠性信息不对称时制造商契约设计

由定理2可知，在信息不对称条件下，高可靠性供应商有可能会伪装成低可靠性类型。为此，制造商要多给高可靠性供应商支付一定的酬金，称为信息租金，表示为：

信息租金表现为高可靠性供应商的可靠性优势，但它只发生在高可靠性供应商谎报自己的类型以选择低可靠性类型契约的情形中。因此，尽管高可靠性供应商接受信息租金，但却表现在低可靠性类型的契约中，因为通过改变低可靠性类型的契约，制造商能改变高可靠性供应商的行为。

在制造上的契约设计模型中，式（5）和式（8）通过改变XH和XL的取值，能够将不等式转化成等式，为紧约束，而式（6）为松约束，用于检验最优解。低可靠性供应商获得的利润πL*=0，高可靠性供应商获得的利润为πH*=(cL-cH)qL+(h-l)(pL+vL)qL，制造商获得的期望利润为：

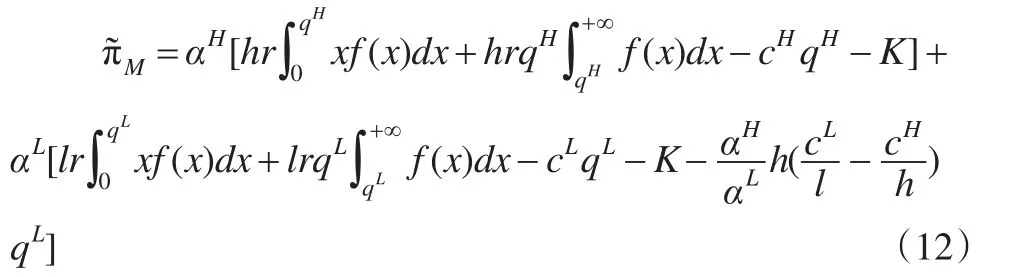
将式（12）自动分离为两种类型供应商各自的非线性规划问题。定理4给出了制造商在供应可靠性信息不对称时的最优契约设计。

定理4：信息不对称条件下，通过设计合理的契约诱导供应商显示其可靠性类型，制造商设计的最优契约（xt，qt，vt，pt）中各决策变量值，如表4所示。

表4 不对称信息条件下制造商设计的最优契约

由定理3和定理4，得到推论1。

由推论1可知：高可靠性契约中的订货量不受私有信息的影响，但在低可靠性契约中，由于私有信息的存在，订货量会有所减少。不论信息是否对称，高可靠性契约中的订货量均大于低可靠性契约中的订货量。据此，定义：

式（3）表示私有信息导致的制造商与低可靠性供应商签约时的渠道损失。

3 信息价值

可靠性信息不对称给制造商造成的损失由信息租金和渠道损失两部分组成。信息租金表现为付给高可靠性供应商的酬金，以引导其表露自己的真实类型；渠道损失表现为私有信息造成的订货量的减少。（而就整体来看，供应链的信息价值只有渠道损失这一部分，信息租金只是在供应链内部进行流转，并不会减少整体的利润。）因此，对制造商而言，其信息价值为：

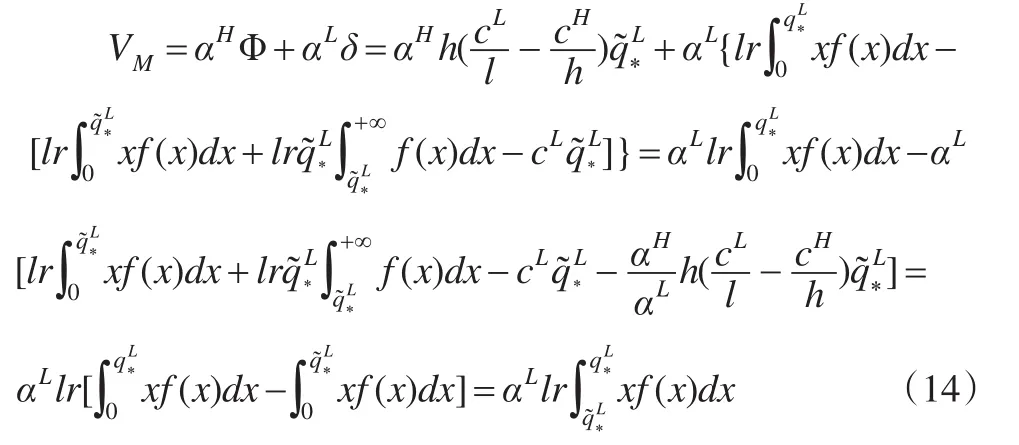
从式（14）可以看出，完全信息和信息不对称下制造商向低可靠性供应商的订货量之差越大，则信息价值越大。

推论2：高、低可靠性供应商之间的可靠性水平相差越大，则信息价值就越大。

推论3：供应商为高可靠性的概率越大，或为低可靠性的概率越小，则信息价值越大。

由推论2和推论3可知，为减弱信息不对称带来的负面影响，制造商可以采取适当的奖惩机制提高低可靠性供应商的可靠性水平，以缩小两种供应商的可靠性差距，或提升高可靠性供应商的比率，将私有信息造成的损失降到最低。

4 算例分析

假定随机需求D服从[10,20]的均匀分布，即D~U[10，20]；两种供应商的可靠性水平分别为h=0.8，l=0.6；两种供应商的市场比例分别为αH=0.4，αL=0.6；两种供应商生产单位产品的成本分别为cH=cL=3；制造商订购费K=5；制造商对两种供应商的单位缺货成本分别为pH=pL=3.5；制造商对两种供应商的单位变动成本分别为vH=vL=1.5；产品的单价r=12。

（1）令αH从0.1依次增加到0.8，则αL依次从0.9降低到0.2，其他参数保持不变。可得可靠性信息不对称情况下制造商最优契约设计和信息价值，如表5所示，制造商契约设计指标与高可靠性供应商的概率αH之间的关系，最后一列反映了αH对制造商信息价值的影响。共享信息使制造商的利润有所增加，即信息不对称使得制造商的利润减少了，且αH越大，则信息价值越大。由第三列数据可知高可靠性契约中的订货量不受私有信息的影响；对比表5（见下页）第3列和第5列数据，可知不论αH取何值，高可靠性下制造商的订货量均高于低可靠性情况。

（2）令h从0.6增加到0.9（h≥l），其他参数保持不变。可靠性信息不对称下制造商的最优契约设计和信息价值，制造商契约设计指标与高可靠性供应商的可靠性水平h之间的关系如表6所示，最后一列反映了h对制造商信息价值的影响，h越大，或两种供应商之间的可靠性水平之差越大，则信息价值越大，即私有信息对制造商造成的利润损失越大。对比表6第2列和第4列数据，可知不论h取何值，高可靠性契约的订货量均大于低可靠性契约。

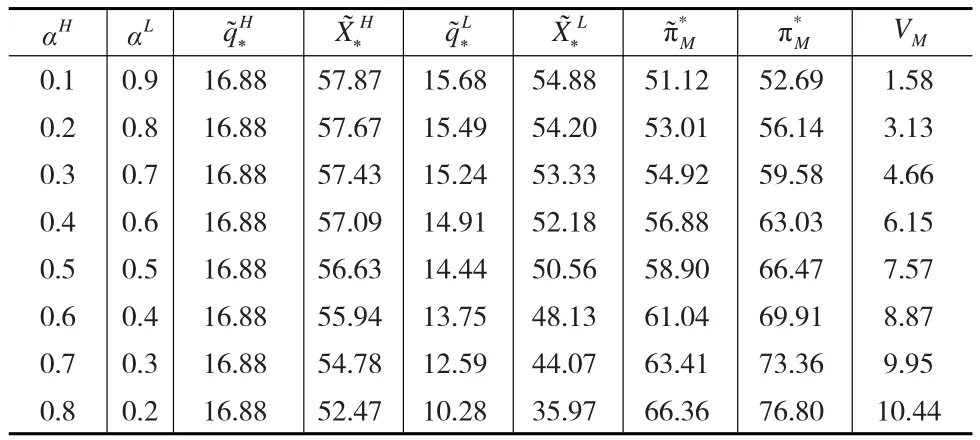
表5 契约设计和信息价值随αH和αL的变化趋势

表6 契约设计和信息价值随h的变化趋势

5 结论

本文研究供应商可靠性信息不对称条件下制造商设计的两阶段动态规划契约以及供应商的生产决策。假定需求随机，供应商的可靠性包含高低两种类型且为其私有信息，运用委托代理理论和显示性原理，研究制造商的最优契约设计和供应商的最优生产安排，探究可靠性信息的获取价值。可得如下结论：

（1）不论信息是否对称，高可靠性契约中的订货量均大于低可靠性契约中的订货量。

（2）高可靠性契约中的订货量不受私有信息的影响，但在低可靠性契约中，由于私有信息的存在，订货量会有所减少。

（3）两种类型供应商之间的可靠性差距越大，高可靠性类型的概率越大，低可靠性类型的概率越小，则获取信息的价值就越大。

本文只研究了单供应商和单制造商的契约设计，并且供应商的可靠性也只限于离散的两种类型，后续可以继续研究多供应商和多制造商背景下的供应链契约设计问题，或者研究可靠性服从连续型随机分布下的采购及协调策略。