基于随机森林的加权特征选择算法

徐少成，李东喜

（太原理工大学 数学学院，太原 030024）

0 引言

面对大量的高维数据，剔除冗余特征进行特征筛选，已成为当今信息与科学技术面临的重要问题，也是人们研究努力的方向。特征选择是从原始特征中根据一定的评估准则剔除一些不相关特征而保留一些最有效特征的过程，且在特征选择后分类正确率近似比选择前更高或近似[1]。Davies证明了筛选最优特征子集是一个NP完全问题[2]。目前，特征子集的选择方法上主要有基于信息熵、神经网络、支持向量机等算法[3-9]。

随机森林（Random forest，RF）[10]是利用多棵决策树对样本进行训练并集成预测的一种分类器，它采用bootstrap重抽样技术从原始样本中随机抽取数据构造多个样本，然后对每个重抽样样本采用节点的随机分裂技术来构造多棵决策树，最后将多棵决策树组合，并通过投票得出最终预测结果。RF对于含有噪声及含缺失值的数据具有很好的预测精度，并且可以处理大量的输入变量，具有较快的训练速度，近些年来已被广泛用于分类、特征选择等诸多领域。

本文以加权随机森林的变量选择特性来研究特征选择算法，用WRFFS算法来进行特征的剔除、筛选，以选出最优的特征子集，相比于文献中的IFN[3]、Relief[4]、ABB[5]、CBFS[6]等特征选择方法，本文算法WRFFS在分类性能（分类准确率、最优特征子集）上均有很大提升。

1 随机森林

定义1[1]：随机森林是由一组基本的决策树分类器合成的集成分类器，其中随机向量序列独立同分布，K表示基决策树的个数。在给出自变量X情况下，每个基分类器通过投票选出最好的分类结果，经过K轮训练，得到一个分类模型序列：

再利用它们构造成一个多分类模型系统，该系统的最终分类结果以多数投票结果为准。最终的分类决策结果：

其中H(x) 表示随机森林的分类结果，hi(x)表示每个决策树分类器的预测分类结果，Y表示分类目标，I(·)表示示性函数。

定义2[1]：给定一组基分类模型序列{h1(X)，h2(X)，…，hk(X)}，每个模型的训练集随机从原始数据集(X，Y)中抽取，因此余量函数为：

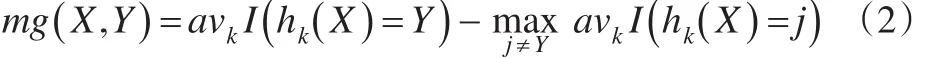
mg(X，Y) 表示余量函数，I(·)表示示性函数，余量函数值反映了正确分类结果超过错误分类结果的程度。

定义3[1]:泛化误差的定义为：

式中,下标X，Y表示概率P覆盖X，Y的空间。

当决策树分类模型足够多时，hk(X) =h(X，θk) 服从强大数定律。

性质1:随着分类模型的增多，对于所有序列θ1，θ2，…，PE*几乎处处收敛于:

性质1说明了随着决策树分类模型的增加，随机森林不会出现模型过度拟合问题，但模型会生成一定程度的泛化误差。

2 随机森林的特征选择算法

本文基于随机森林来设计特征选择算法，采用袋外数据(记为OOB)做测试集。本文算法是利用重抽样技术构造多个数据集，分别在每个数据集上进行特征重要性度量，然后给每个特征重要性度量加上权值，最后综合评估特征重要性度量。

2.1 算法描述

本文的算法WRFFS，利用特征重要性度量值作为特征排序的重要依据，依次从特征中去掉一个重要性最低的特征，并计算每次剔除后的分类正确率，选取最高正确率对应的特征变量作为最优特征选择结果。为了消除数据不均衡带来的大偏差影响，本文采用10折交叉验证计算分类正确率，取10次分类的平均正确率作为本轮迭代的分类正确率。其中以10次训练中最高正确率对应的训练数据作为进行特征重要性排序的原始数据。

算法的具体过程如下（注：N代表原始数据中特征的总数）：

输入：原始数据集S；

最大分类正确率MaxAcc=0

过程：for t=1,2,…,N-1

1：将原始数据集S随机均分成10份；

2：设置局部的平均分类正确率MeanAcc=0；

3：for i=1,2,…,10

4：初始化每次迭代的正确率为Acc=0；

5：在数据集S上运行randomForest创建分类器；

6：在验证集上进行分类；

7：比较分类结果，计算每次迭代的分类正确率Acc；

8：计算平均分类正确率，MeanAcc=MeanAcc+Acc/10；

end for

9：对特征按重要性度量进行排序；

10：比较 if(MaxAcc<=MeanAcc)

则(MaxAcc=MeanAcc)；

11：剔除特征重要性排序中最不重要的一个特征，得到新的数据集S；

end for

输出：全局的最高分类正确率MaxAcc；

全局的最高分类正确率对应的特征选择集合

2.2 特征重要性度量

本文基于OOB样本数据来做特征的重要性度量。为了避免OOB数据类别严重不均给算法结果带来的影响，本文采用K折交叉验证来计算特征的重要性度量值。本文WRFFS方法在计算特征的重要性度量值时，通过分别在每个特征上添加噪声然后进行分类正确率的对比，来确定特征的重要性程度（当一个特征很重要时，添加噪声后，预测正确率则会明显下降，若此特征是不重要特征时，则添加噪声后对预测的准确率影响微小）。本文K的取值采用简单的交叉验证思想，将K取值为5，取5次的平均值作为最终的性能评价标准。

设原始的数据集为D，特征个数为N，经过重抽样后的数据集为Repeated Sampling-D(简记为RS-D)，个数为M。

随机森林的Bagging步骤就是对原始数据进行Bootstrap取样，为了保证分类的精度，WRFFS经过多次重复取样构造多个数据集。在每个RS-D数据集上构造一棵决策树，通过给特征添加噪声对比分类正确率，得到一个特征的重要性度量。M个RS-D数据集可以得到M个特征的重要性度量。但是每个RS-D数据所获得的特征重要性的可信度（权重）不同。因此WRFFS方法的主要步骤就是计算特征的重要性度量值和权重的大小。

第j个属性的特征重要性度量是由R和Rj的差值所决定的，其中R表示的对特征添加噪声前的分类正确的个数，Rj表示的对特征添加噪声后的分类正确的个数。由于采用的是五折交叉验证，每个RS-D数据集分成五份，五份数据集交叉作为测试数据集，因此在同一RS-D数据集上，R和Rj需要分别计算五次，最后第j个特征的重要性度量FMij是由五次产生的平均差值来决定：

其中i代表第i个RS-D数据集，j代表第j个特征，k代表第k层数据。

2.3 权重度量

假设存在一个样本数为T的测试数据集，有M个不同的RS-D数据集产生M棵决策树。根据决策树的预测结果可以获得一个T×( )M+2 的矩阵，矩阵的每行代表着要预测的样本，矩阵的前M列分别表示M棵决策树对每个样本的预测结果，第M+1列代表前M棵决策树对每个样本综合投票的结果（前M列中每行中占多数的样本分类结果判定为该样本的最终分类结果放在第M+1列），第M+2列代表测试数据的真实分类结果。则第i棵决策树的可信度（权重）可由下列公式得到：

其中TreeConfidencei表示第i棵决策树的权重，Treeij表示第i棵决策树对第j个样本的预测结果，Ensemblej表示所有决策树对第j个样本的集成预测结果。AccEnsemble表示集成预测的准确率，即Ensemble与Original的相符程度。由于每棵决策树的AccEnsemble值都是一样的，因此是否考虑AccEnsemble的作用对排序结果没有影响，但本文在计算权重时加入这个因素，其目的是尽量缩小各决策树间权重的相对差距。

表1（见下页）是一个M=7，T=5的一致性度量矩阵。

表1 M=7，T=5的一致性度量矩阵

表1列出了7棵决策树分别对5组数据的分类结果，Ensemble对应那一列为7棵决策树分别对5组数据的集成结果，以超过半数的结果作为最终的集成结果，Original对应那一列分别为5组数据的真实分类标签。

若不考虑AccEnsemble因素，根据可信度公式分别计算出来Tri的可信度：

TreeConfidence1=1，TreeConfidence2=0.4，TreeConfidence3=0.8，TreeConfidence4=0.8，TreeConfidence5=0.2，TreeConfidence6=0.6，TreeConfidence7=0.6

若考虑AccEnsemble因素，根据可信度公式分别计算出来Tri的可信度：

AccEnsemble=0.8

TreeConfidence1=0.8，TreeConfidence2=0.32，TreeConfidence3=0.64，TreeConfidence4=0.64，TreeConfidence5=0.16，TreeConfidence6=0.48，TreeConfidence7=0.48

所以最终的特征重要性度量值FinalMetric可通过下式计算：

其中j表示第j个特征。

3 实验结果及分析

3.1 实验数据

为了方便比较和分析，在UCI数据集文献[11]中挑选了8个具有代表性的数据集。表2列出了这些数据集的特征。

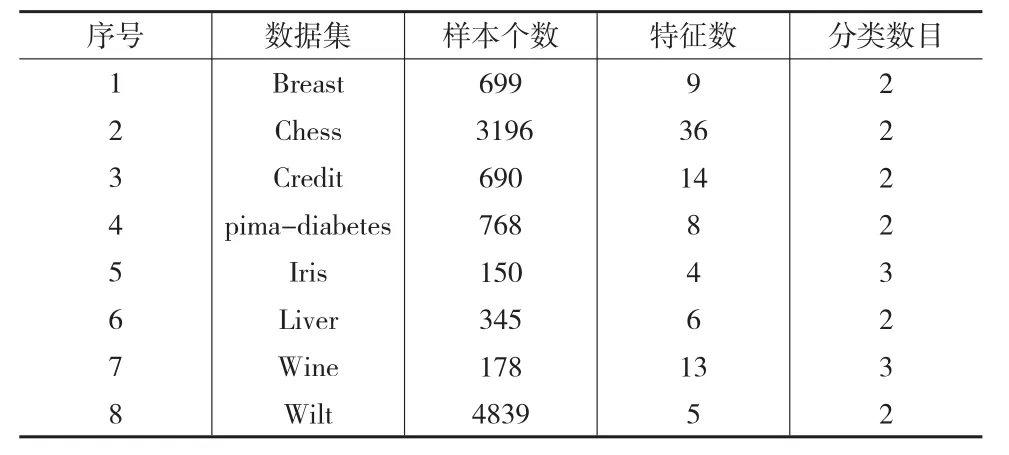
表2 取自UCI的实验数据汇总

3.2 实验结果

在每个数据集上，运行本文的特征选择算法WRFFS，记录在每个数据集上进行特征选择后挑选出的最优特征子集及对应的分类正确率。表3和表4分别给出了这些数据总特征数及在 IFN、Relief、ABB、CBFS、WRFFS算法下进行特征重要性排序而得到的最优特征集的大小。表中最后一列给出了本文WRFFS算法选出的最优特征子集。为了验证WRFFS在选择特征时的稳定性，表3的WRFFS方法在计算特征重要性度量时进行特征值干扰的方式是添加高斯噪声，表4的WRFFS方法在计算特征重要性度量时进行特征值干扰的方式是扰乱特征值。

表5列出了随机森林在IFN、Relief、ABB、CBFS、WRFFS算法下进行特征选择后的分类错误率，最后两列列出了本文方法WRFFS在两种不同的噪声干扰下经过特征选择后的分类错误率。表中第一列为本文方法在数据集上进行特征选择前的分类错误率。

表3 各个算法得到的特征子集的大小（添加高斯噪声）

表4 各个算法得到的特征子集的大小（扰乱特征值）

表5 随机森林在全部特征及进行特征后的特征子集上的分类错误率（%）对比

通过对表3、表4的特征选择结果和表5的分类错误率分析，尽管用不同类型的噪声来扰动特征属性值，但他们最终选择的特征子集和分类错误率却是几乎一致的，这也说明了本文的方法WRFFS在特征选择上是稳定的。再对比本文的WRFFS和IFN、Relief、ABB、CBFS在最终选择出的子集特征维数看，IFN、Relief、ABB选择出的特征维数平均下降了大约30%以下，CBFS选择出的特征维数平均下降了大约48%，而WRFFS选择出的特征维数平均下降了大约50%。除了CBFS和WRFFS选出的特征子集维数相差不多外，IFN、Relief、ABB选择出的特征子集维数下降率明显低于WRFFS方法，说明本文的WRFFS在特征选择数目上具有一定的优势。

分析表5中的数据发现，IFN、Relief、ABB、CBFS经过特征选择后的平均分类错误率大约在15%左右，而本文的WRFFS经过特征选择后的分类错误率却只有10%左右，相比其他方法的分类错误率下降了30%多。尽管CBFS选择的特征子集维数和WRFFS方法几乎一致，但WRFFS在特征选择后的分类错误率比CBFS降低了30%多。WRFFS相比特征选择前分类精度有些许下降，是因为特征选择尽管去掉了一些不重要的特征，但也去掉了这些特征所包含的分类信息，所以分类精度稍许有些下降也是正常的。

综合以上两方面，本文的WRFFS不管在特征选择的数目上还是在分类精度方面，WRFFS都较其他方法有很大的优势。由于选取的数据具有广泛的代表性，所以说WRFFS在特征选择上具有更强的适用性。

4 结束语

为了对大量高维数据进行降维以筛选出最优特征子集，本文提出了基于随机森林的加权特征选择算法WRFFS。加权的思想主要体现在进行特征的重要性度量时，以往方法只对一个数据集利用决策树进行一次特征重要性度量，本文方法通过对原始数据集重抽样构造多个小数据集，在每个小数据集上分别作一次特征重要性度量，然后对所有子数据集上的特征重要性度量值加权求和得到最终的特征重要性度量值。该算法以特征重要性度量为标准对特征按重要性程度进行排序，然后采用SBS法依次剔除排在最后一位的最不重要的特征，最后基于分类正确率挑选出最优特征子集。实验结果表明WRFFS具有很好的性能（特征选择子集少，分类精度高），与文献中的方法[3-6]相比具有很大的优势。所以WRFFS在特征选择上具有更强的适用性。

由于WRFFS采用后向序列搜索法依次剔除排在最后一位的一个最不重要的特征，在面对高维或者超高维的大数据时，本文方法WRFFS效率不是很高。所以在后续的研究中可以从每次过滤掉不重要特征的数量上来提高算法整体的效率和性能。