带有Elastic Net惩罚的贝叶斯分位数回归及其数值模拟

刘亚新

（中南大学 数学与统计学院，长沙 410083）

0 引言

自1978年Koenker和Bassett[1]提出分位数回归的概念以来，分位数回归因能提供更全面的信息以及优良的性质，在理论和应用领域都得到了广泛的研究和应用。Yu和Moyeed[2]最早提出了贝叶斯分位数回归，将分位数回归问题与非对称拉普拉斯分布（Asymmetric Laplace Distribution,ALD）联系起来，分位数回归系数估计的最小化问题等价于误差项服从非对称拉普拉斯分布的似然函数的最大化问题，进而采用贝叶斯方法估计分位数回归的系数，该方法在计量经济学领域受到了越来越多的关注。由于似然函数很复杂，参数的后验分布不是熟悉的函数形式，因此常常用MCMC方法对参数的后验分布进行抽样模拟，得到参数的贝叶斯估计。Yu和Moyeed采用的是随机游走M-H算法，建议分布为以当前参数值为均值的正态分布。尽管该方法非常方便地产生候选值，但是接受率依赖于分位数，而且收敛速度很慢。Kozumi和Koboyashi[3]提出了基于非对称拉普拉斯分布的位移-尺度模型的Gibbs抽样算法。该算法根据参数的全条件后验分布进行抽样，而全条件后验分布是已知的函数形式，这大大提高了抽样的收敛速度，因此得到了广泛应用。

对分位数回归中的变量选择问题，Koenker[4]首次将Lasso的思想应用于分位数回归中。Wang等[5]将最小绝对差估计与自适应Lasso惩罚结合起来进行变量选择。Li和Zhu[6]将Lasso的思想应用于分位数回归中进行变量选择，将系数的绝对值和作为惩罚部分，提出了计算Lasso分位数回归的全部正则化路径的有效算法，同时又对拟合模型的有效维数进行估计，可以用来选择正则化参数。Wu和Liu[7]证明了SCAD方法和自适应Lasso分位数回归的Oracle性质。Park和Casella[8]从贝叶斯角度研究Lasso分位数回归问题，提出了分层模型，并用Gibbs抽样进行参数估计。Li等[9]从贝叶斯的角度研究Lasso分位数回归，提出了一个分层模型的框架，将参数的先验分布设成拉普拉斯先验，并用Gibbs算法进行抽样，实验证明贝叶斯Lasso分位数回归比其他方法的Lasso分位数回归更优。Alhamzawi等[10]提出了贝叶斯自适应Lasso分位数回归，对不同的回归系数赋予不同的惩罚参数，且惩罚参数的先验设为倒伽玛分布，并把倒伽玛分布的超参数设成未知量，采用Gibbs算法对后验分布抽样来估计参数。

本文对带有Elastic Net惩罚的贝叶斯分位数回归提出了更简单的估计方法，使所有参数的全条件后验分布都是熟知的分布形式，可以采用Gibbs算法进行抽样，避免了Gibbs抽样中又包含M-H抽样的问题[9]，提高了迭代效率。

1 带有Elastic Net惩罚的贝叶斯分位数回归

1.1 分位数回归

给定训练数据{(xi,yi),i...,n},xi为预测变量，yi为响应变量，预测变量xi与响应变量yi满足：

其中β=(β1，β2，...，βk)T∈Rk,εi是误差项，且相互独立，满足εi的第τ分位数为0，即的τ分位数回归方程可以写为：

根据Koenker和Bassett[1]的理论，分位数回归系数β的求解可转化为下列优化问题：

其中ρτ(u)=u(τ-I(u＜0))是损失函数，I(·)表示示性函数。

Yu和Moyeed[2]指出，在假设误差服从非对称拉普拉斯分布的前提下，最小化问题（3）可以转化为最大化似然函数问题。即假设误差项εi服从非对称拉普拉斯分布ALD(0，σ，τ)，其中σ是尺度参数，εi的密度函数为：

可以证明，服从该分布的变量的τ分位数是0。进而yi|xi，β，σ~ALD(，σ，τ)，密度函数为：

样本集y=(y1，y2，...，yn)T的似然函数为：

需要说明的是，误差ε并不是真的服从ALD分布，这样的假设只是为了将最小化问题（3）转化为最大化似然函数（4）。不管数据的原始分布是什么，使用非对称拉普拉斯分布都是一种有效的拟合贝叶斯分位数回归的方式，即使误差不是真的服从非对称拉普拉斯分布，参数估计仍能取得很好的效果。

1.2 基于Elastic Net惩罚的贝叶斯分层模型

带有Elastic Net惩罚的分位数回归的参数估计模型为：

由于：

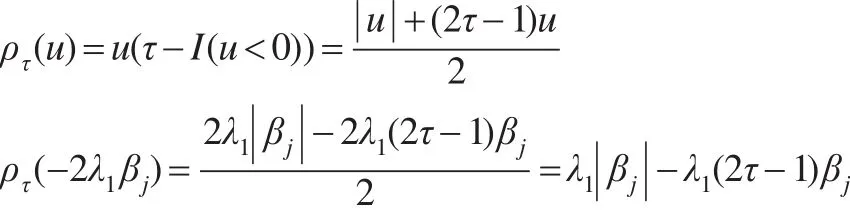
式（5）可以转化为:

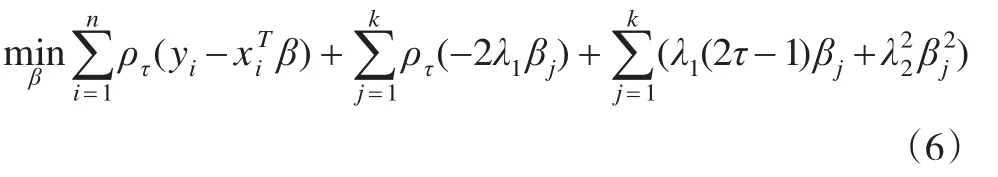
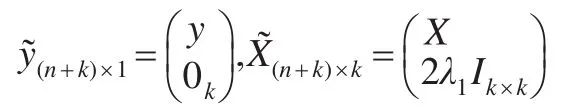
其中X=(x1，x2，…，xn)T，Ik×k表示k阶单位矩阵，则式（6）将变为:

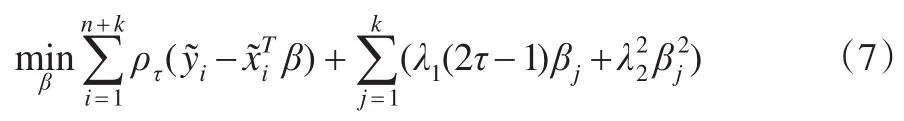
令:

则:

可以看出，最小化式（7）相当于最大化式（8）。令η=，为了得到各参数的全条件后验分布，将非对称拉普拉斯分布用指数分布和正态分布混合表示。Kozumi和Kobayashi[11]已证明，若z服从指数分布exp(τ(1-τ)σ)，v服从标准正态分布N(0,1)，误差项可以表示为:

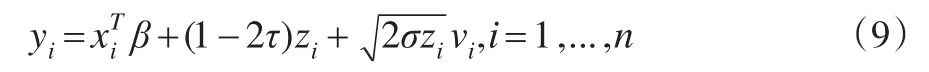
从而:yi|xi，zi，β，σ~N(+(1-2τ)zi，2σzi)

为了得到参数的贝叶斯估计，需要指定各参数的先验分布。本文对尺度参数σ，惩罚参数(λ1，η)分别采用各自的共轭先验分布，σ的先验分布为倒伽玛分布IG(a，b)，λ1的先验分布为N(μ，δ2)I(λ1＞0)，η的先验分布为广义倒高斯分布GIG(c，d，f)，其概率密度函数为:

则式（1）将转化为:

其中Kc是第二类修正贝塞尔函数，d＞0，f＞0，c是实数。

外墙保温性能的高低，将会直接影响旧工业建筑改造后日常运营中的能耗，利用原有厚砖墙的畜热性能在此基础上采取修复、增加保温层等措施进行外墙的改造设计。一般情况下，旧工业建筑的外窗气密性和保温性能差，应进行节能计算采取相应的改造更换措施，将原单层平板玻璃更换位为中空低辐射节能玻璃。屋顶保温性能设计。采取更新原来保温层的办法进行改造设计。

综上所述，得到如下的贝叶斯分层模型：

1.3 Gibbs抽样

由贝叶斯分层模型可得，参数 (β，σ，λ1，η，z)的联合后验密度为：

根据贝叶斯定理，回归系数βj的全条件后验密度为：

其中β-j表示去除参数βj之后的参数向量，xi，-j也类似，则βj的全条件后验分布为正态分布N(ba′，1a′)。

参数σ的全条件后验密度为：

故参数σ的全条件后验分布为倒伽玛分布，即：

同理可得其他参数的全条件后验分布分别为：

由各参数的全条件后验分布可以采用Gibbs算法进行抽样，其中广义倒高斯分布的抽样可以参考Dagpunar[12]和Jörgensen[13]，也可以借助 R软件中GeneralizedHyperbolic程序包中的rgig函数。

2 数值模拟

2.1 独立同分布情形

对于独立同分布情形，本文采用在这一研究领域经常使用的数值模拟模型：

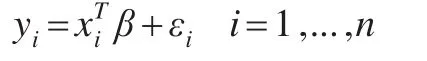
其中回归系数分为以下两种形式：

Case1：β=(3，1.5，0，0，2，0，0，0)T

Case2：β=(0.8，0.8，0.8，0.8，0.8，0.8，0.8，0.8)T

Case1和Case2分别对应稀疏和密集的情形。在Case1中，自变量的样本数据产生于多元正态分布Nk( )0，Σx，误差ε~N(0，1)。在Case2中，自变量的样本数据产生于多元正态分布误差ε~N(0，1)。模型生成20组数据集，每组数据集中有400条训练样本，100条测试样本。评价指标为对测试样本计算的均值绝对差的均值（MMAD）和标准差（SD），即：

分别估计分位数τ=(0.3，0.5，0.8)时的分位数回归模型。

表1和表2（见下页）分别是独立同分布情形下Case1的参数估计结果和MMAD（SD）值。可以看出，在参数估计方面，带Elastic Net惩罚的分位数回归方法比QRLasso方法和QR-SCAD方法更准确，但是其MMAD值和SD值比这两种方法都大，而只比QR方法小，说明当预测变量之间的相关性较低时，带Elastic Net惩罚的分位数回归方法的优势并不十分明显。

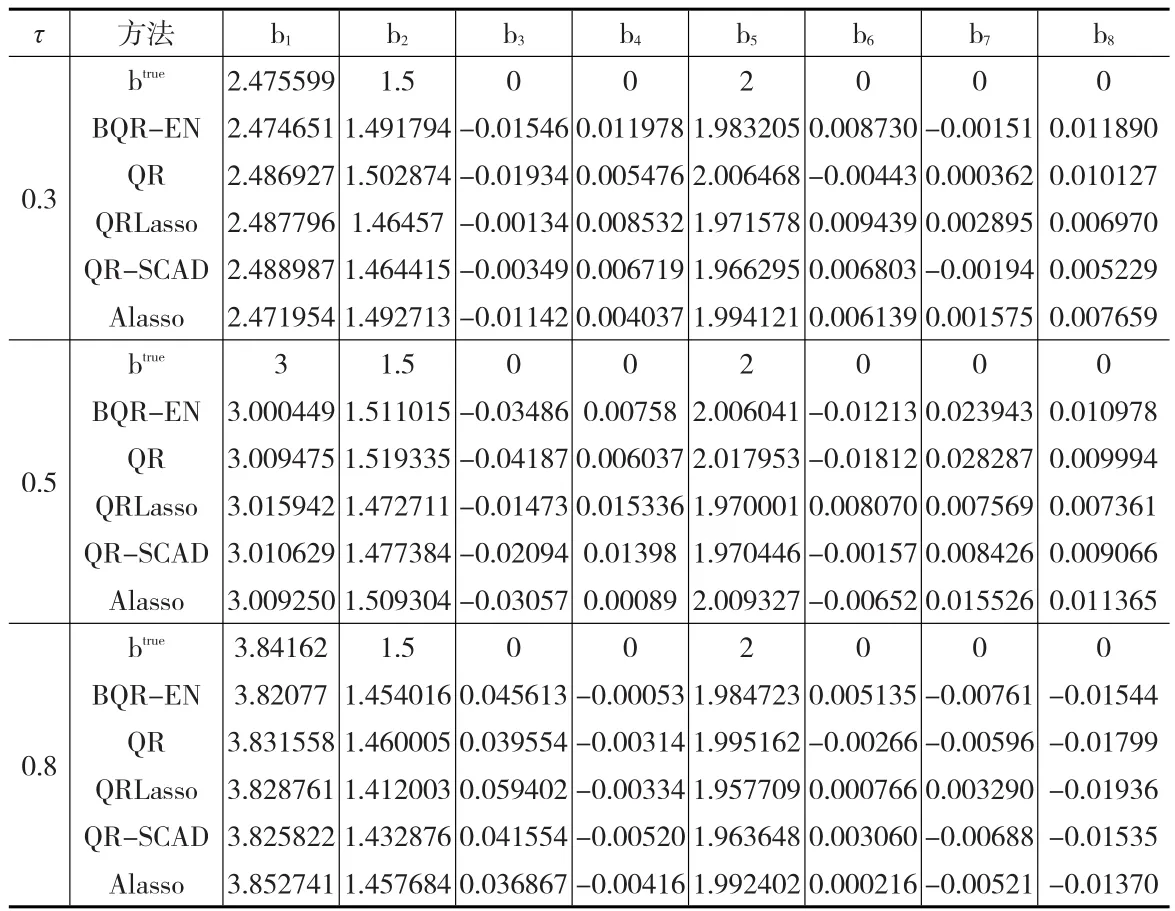
表1 独立同分布情形下Case1的参数估计

表2 Case1各方法的MMAD(SD)值

表3和表4分别是独立同分布情形下Case2的参数估计结果和MMAD（SD）值。Case2对应密集的情形，并且变量之间存在较高的相关性，可以看出带Elastic Net惩罚的分位数回归方法凸显出了优势，其MMAD(SD)值比其他四种方法都要小，而且参数估计也相对更加准确。这说明带Elastic Net惩罚的分位数回归方法在变量之间存在比较严重的多重共线性时具有明显的效果，同时也具有较强的稳健性。

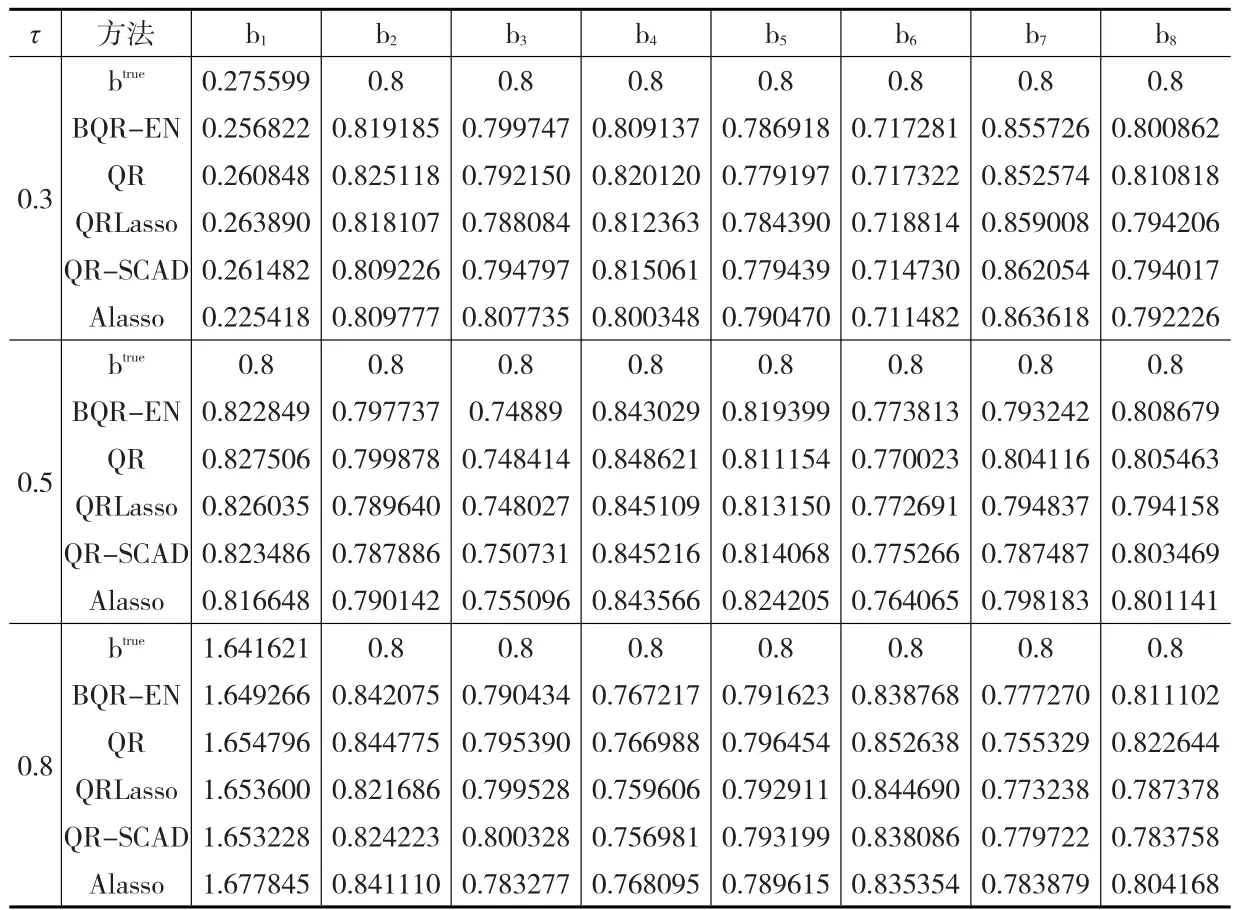
表3 独立同分布情形下Case2的参数估计

2.2 非独立同分布情形

对于非独立同分布下的数值模拟，本文采用如下回归模型：

预测变量x1，x2，…，x7的样本数据产生于均匀分布U(0 ，1) ，误差项ε~N(0 ，1)。与独立同分布情形类似，模型生成20个数据集，每个数据集中有400条训练样本，100条测试样本，估计分位数τ=0.2，0.3，0.5下的分位数回归方程。

表5和表6（见下页）分别是非独立同分布下的参数估计结果和MMAD（SD）值。可以看出，在非独立同分布下，五种方法仍能得到比较准确的估计。其中，本文的方法在预测方面具有较小的标准差(SD)，总体上要优于QR方法和QRLasso方法。Alasso方法虽然比带Elastic Net惩罚的分位数回归方法有更小的MMAD值和SD值，但是其不能解决预测变量个数大于样本量这种情况，而且Alasso方法的惩罚参数多，抽样复杂，没有带Elastic Net惩罚的分位数回归方法便于理解，易于操作。

表4 Case2各方法的MMAD(SD)值

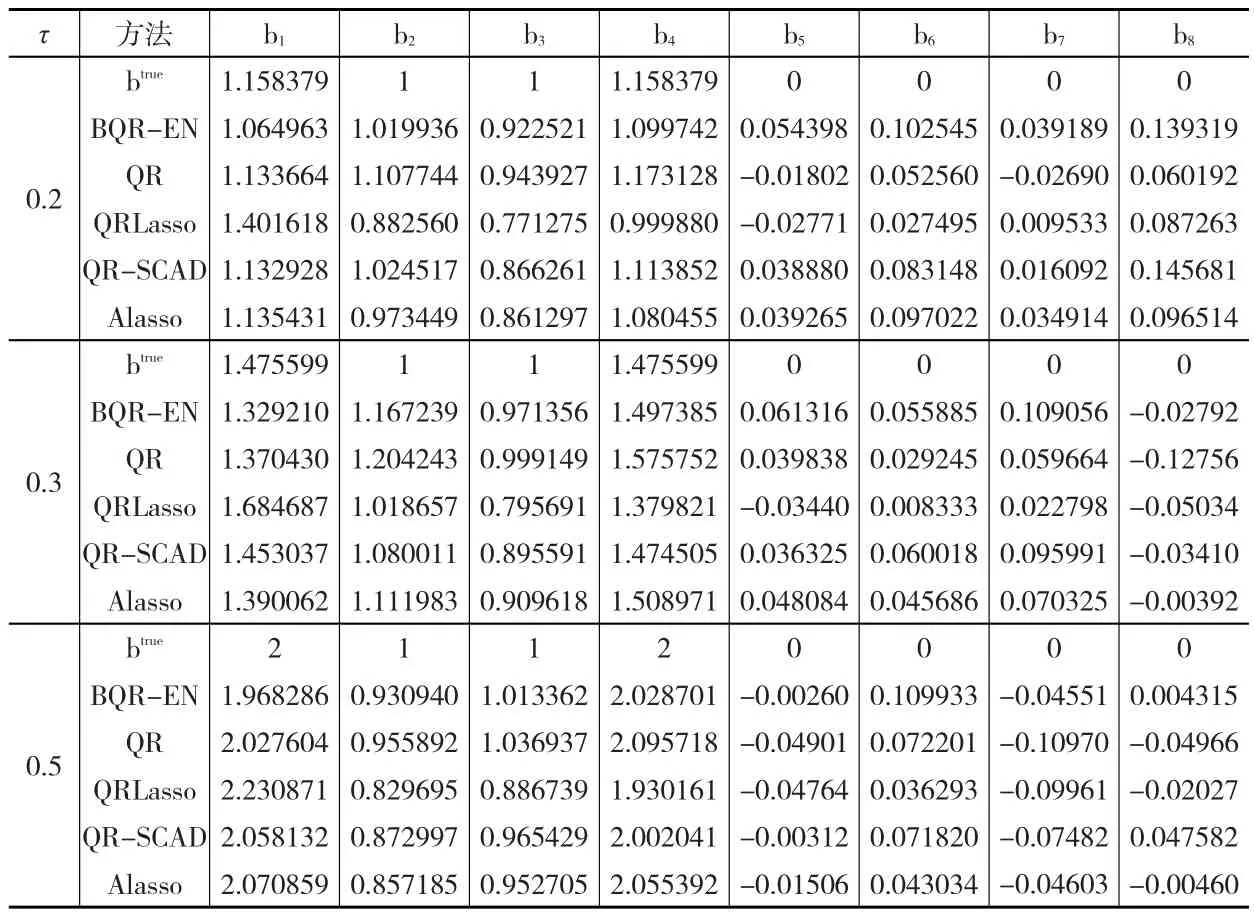
表5 非独立同分布情形下的参数估计

表6 非独立同分布情形下各方法的MMAD(SD)值

3 结论

带有Elastic Net惩罚的参数估计方法是对Lasso方法的改进，可以解决预测变量大于样本量情况下的变量选择问题，并且当预测变量间存在着较高相关性时，Elastic Net惩罚仍然能得到比较准确的参数估计。本文研究了带有Elastic Net惩罚的贝叶斯分位数回归问题，建立了相应的贝叶斯分层模型，使Gibbs抽样成为可能，提高了马尔科夫链的收敛速度，同时在参数估计和预测方面也具有较小的偏差。