基于贝叶斯理论的云模型参数估计研究

高艳苹，吕王勇，王玲玲，蔡琳芝

（四川师范大学 数学与软件科学学院，成都 610068）

0 引言

云模型由三个云参数期望Ex、熵En、超熵He构成，并且自1995年由李德毅院士提出至今有着十分广泛的应用，包括智能控制[1]、数据挖掘[2,3]、多属性决策[4,5]和分析评价[6]等。这些应用领域大部分将精确的数量值变为定性的语言值，这种转换最关键的部分就是通过精确的数量值估计出云参数值。经典的云参数估计方法有矩估计法和极大似然估计法，二者的共同点是在将样本均值作为期望估计值的前提下，分别求得熵、超熵的矩估计和极大似然估计。在期望不是一个未知参数，而是一个随机变量，且分布已知的假设下，应用贝叶斯理论，得到期望的后验分布及其后验估计，然后通过期望的后验估计求得熵、超熵的后验矩估计和后验极大似然估计。贝叶斯理论在云模型中的应用除此之外还包括：空战态势评估[7]、空中目标威胁评估[8]、公路物流供应链整体协调[9]、航空发动机性能评估[10]等。

本文将Ex作为一个随机变量，根据其先验分布推得其后验分布与后验估计；再根据Ex的后验估计得到关于En、He的后验矩估计和后验极大似然估计；最后运用均方误差准则，通过仿真实验对这几种估计方法加以比较，得到后验的极大似然估计法效果最优的结论。

1 云模型

1.1 云模型的定义及基础知识

云是利用自然语言值表示的某个定性概念A与其定量表示之间的不确定性的转换模型。设U是一个用精确数值表示的论域，A是U上对应的定性概念，对于任意的x∈U，都存在一个[0，1] 区间上具有稳定倾向的随机数μA(x)，μA(x)叫做x对A概念的确定度，x在论域上的分布称为云模型，简称为云。云由数字特征期望Ex、熵En、超熵He来反映定性概念整体上的定量特征[11]。期望Ex是整个论域的重心，也是概念量化的最典型样本；熵En是概念A不确定性的度量，熵越大，概念越宏观，模糊性和随机性也越大；超熵He是熵的不确定性度量，即熵的熵。云将定性概念的整体特性用三个数字特征值来定量反映，对理解定性概念的内涵和外延有着极其重要的意义，而且通过三个数字特征，可以设计不同的算法来生成云滴及其确定度，得到不同的云模型[11,12]。

在云模型中，两个最关键、最重要的算法是正向云算法[11]和逆向云算法。正向云算法是在已知云模型的三个参数Ex、En、He值的情况下，产生带有确定度的云滴样本。逆向云发生器是根据一定数量的云滴样本得到表征定性概念的三个参数Ex、En、He的值。两种算法综合应用，共同实现定性语言值与定量数值之间的自然转换。

由于正态云的普适性[12]及其在云模型中的重要地位，所以本文主要研究正态云模型。在正态云中，设X是一随机变量，且X～N(Ex，y2)。

其中：

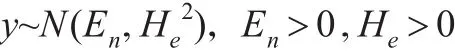
则y的概率密度函数为：

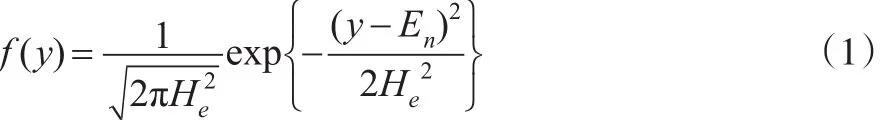
当y为定值时，X的条件概率密度函数为：

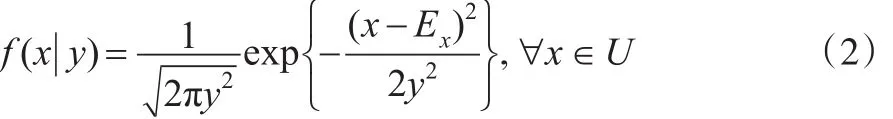
根据式（1）和式（2），又由条件概率密度公式[13]，可知X的概率密度函数：

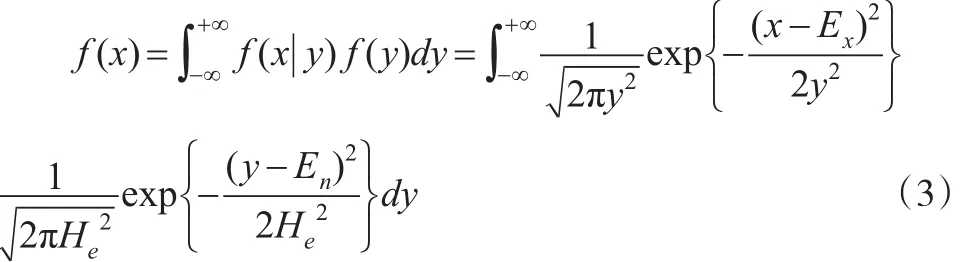
由此可得[14,15]：

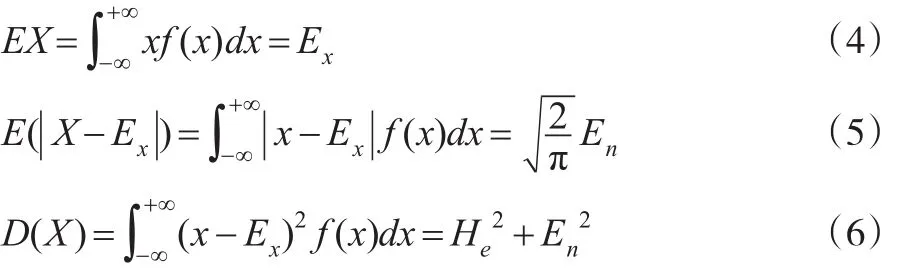
1.2 云滴的产生过程

云滴的产生过程如下：

（1）生成期望值En、标准差He的正态随机数y；

（2）生成期望值Ex、标准差y的正态随机数x；

产生云滴之后需要将这些云滴送入云滴检验器，通过检验的云滴才可以使用。

1.3 云滴检验器

（1）因为云滴服从N(Ex，En2+He2)的正态分布，由中心极限定理知，当时，定型概念的确定度可以达到1-α，其中为标准正态分布的双侧百分位点。计算出的云滴点的均值XL和的云滴点的均值XH。当满足时：其中d=XH为在给定α时定性概念覆盖达到1-α的范围，则可认为云滴聚集度较高，即专家意见差异较小，可以接受，若不符合，需要修正[16]。

（2）将置信范围1-α之外的云滴去除，利用初始的Ex、En、He重新生成等量的云滴。

（3）将新生成的及没被剔除掉的云滴样本，运用矩估计[15]，得到新的参数Ex、En、He的估计值。

有了样本并且对样本进行了检验，通过检验的样本就可以进行云参数的估计，下面介绍两种经典的云参数估计方法。

2 经典的云参数估计方法

2.1 云参数的矩估计

设x1，x2，…，xn是来自随机变量X且通过检验的一簇云滴样本，根据式（4）至式（6）并结合样本求得云参数的矩估计如下：

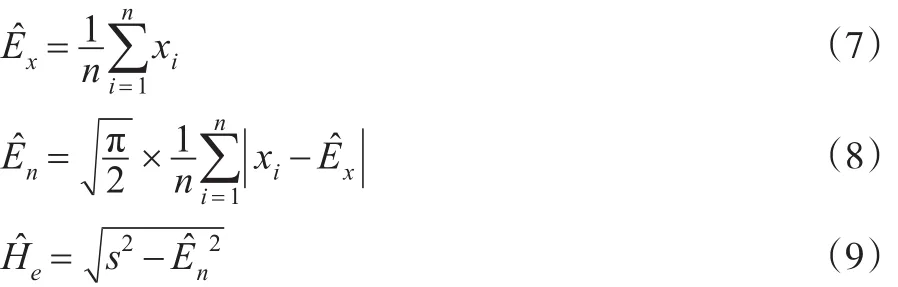
2.2 云参数的极大似然估计

沿用上面的假设，x1，x2，…，xn是来自X并且通过检验的一簇云滴样本，X～N(Ex，y2)，y～N(En，He2)。因为云模型共有三个未知参数，其中样本均值是参数Ex的无偏估计，所以在这里参数Ex的估计值依旧使用样本均值代替，即由式（3）知X的密度函数为：

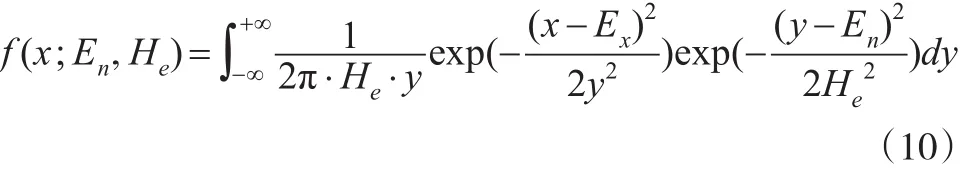
所以这组样本点的似然函数为：

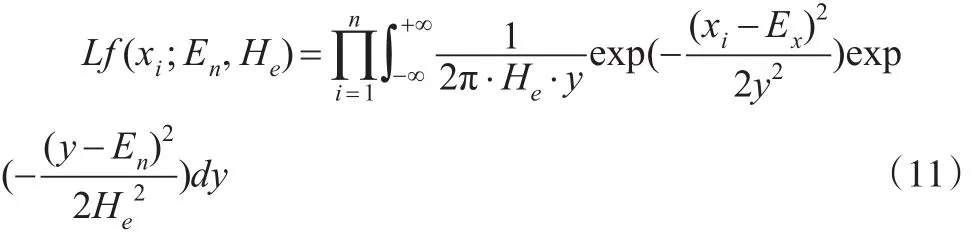
记：

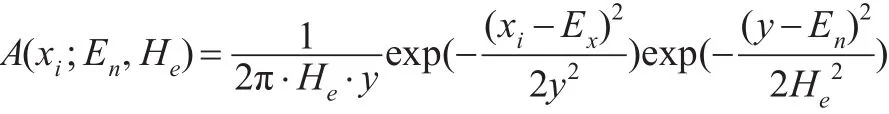
将式（11）取对数，得到：

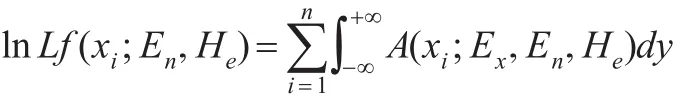
然后将式（11）分别对He，En求导，得到：

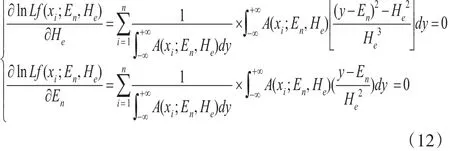
满足式（12）的解就是En，He的极大似然估计。

不管是矩估计还是极大似然估计，在对参数Ex进行估计时都是用的样本均值。假设Ex不是一个未知参数，而是一个随机变量，并且知其先验分布，那么就可以应用贝叶斯理论得到Ex的后验分布，下面给出Ex的后验分布推导过程及参数的后验估计。

3 云模型中Ex的后验分布与参数的后验估计

3.1 Ex 的后验分布

设x1，x2，…，xn是来自X并且通过检验的一簇云滴样本，其中En，He是未知参数。假设Ex的先验分布服从正态分布，这里的c0表示Ex的期望，是Ex的方差，可得样本X的分布和Ex的先验分布分别为：

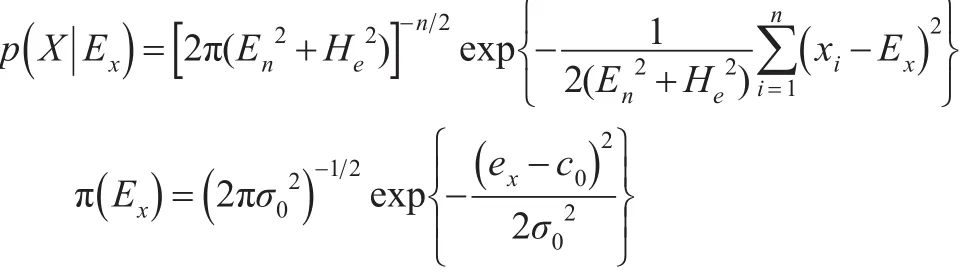
由此可以写出X和Ex的联合分布：

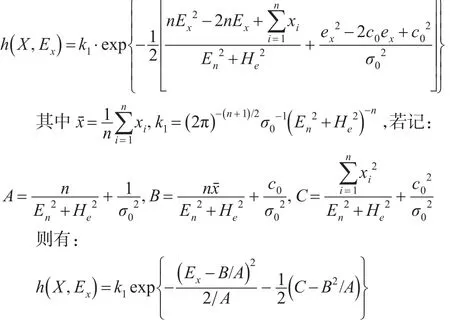
可见A、B、C均与Ex无关，由此容易算得样本的边际密度函数和Ex的后验分布：

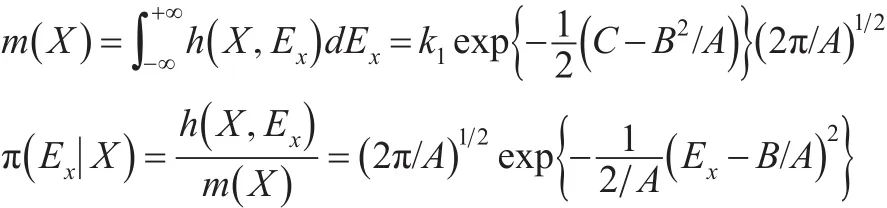
这说明在样本给定后，Ex的后验分布为,即：

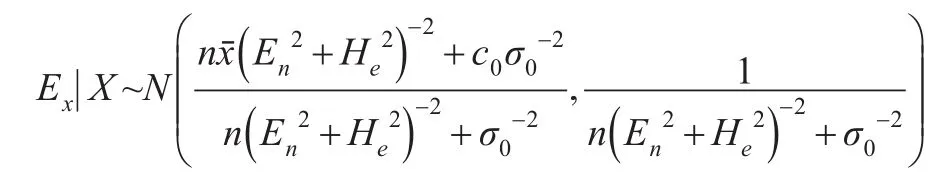
后验分布的均值即为Ex的后验估计，记为

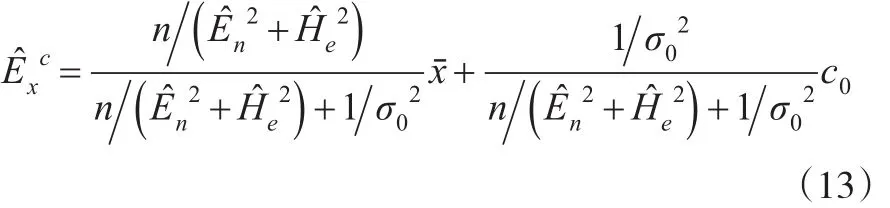
其中，是En，He的矩估计。有了Ex的后验估计就可以得到参数En、He的后验矩估计和后验极大似然估计。

3.2 En、He 的后验矩估计

公式（13）是Ex的后验估计，再根据式（5）和式（6）得到En、He的后验矩估计为：

其中s为云滴的样本标准差。

有了Ex的后验估计，也可以据此构造参数En、He的后验极大似然估计。

3.3 En、He 的后验极大似然估计

上文给出了求得En、He极大似然估计的方法，后验的En、He的极大似然估计法与其原理相同，唯一不同的是，经典的En、He极大似然估计所使用的Ex的值是由样本均值代替的，后验的En、He的极大似然估计所使用的Ex的估计值是通过贝叶斯理论得到的，将Ex的后验估计值带入到公式（12）中，求得满足方程组的解就是En、He的后验极大似然估计。

4 仿真

无偏性是对估计量的一个重要而常见的要求，但是很多时候无偏估计是不存在的，也不一定比有偏估计更优。从直观上理解，一个好的估计应该在真值周围波动，同时拥有较小的均方误差，所以均方误差也是一个评价估计优劣的有力标准。本文用均方误差综合评价估计的优劣。

设初始云参数为Ex=25，En=3，He=0.1，并用此组值产生云滴样本。剔除掉隶属度大于99.99%的样本点和偏离很大的云滴样本，然后等数量取样，将重新得到的云滴加上没被剔除的云滴送入到云滴检验器进行检验云滴，检验通过的云滴样本进行计算。根据云滴样本容易求得经典的云参数的矩估计值；在使用经典的云参数的极大似然估计方法时，由于式（12）是无穷积分，所以根据6σ原则[13]，将无穷积分变为定积分，利用复合梯形求复杂定积分的方法计算式（12）中的每一个积分，而后将En、He设定区间和步长，每取一次En、He的值，带入到计算后的积分中，找到使式（12）结果最接近0的En、He的值，那么这组En、He即为所求。

在求Ex的后验估计时，En、He的值是已知的，即为参数En、He的矩估计值；然后根据求得的Ex的后验估计得到了En、He的后验矩估计。En、He的后验极大似然估计就是将式（12）中Ex的值用Ex的后验估计值代替，其余的求解方程组的步骤与经典的极大似然估计求解步骤相同，最后得到的使式（12）结果最接近0的En、He的值就是En、He的后验极大似然估计。

四种算法下熵En和超熵He的均方误差比较如下页图1和图2所示。

图1是四种算法下熵En均方误差的比较。由图1可知，经典熵的矩估计的均方误差最大，熵的后验极大似然估计的均方误差最小，所以四种算法中熵的后验极大似然估计算法效果最优。参数的矩估计随着样本量变化的增加波动较大，而极大似然估计的波动较为平缓，且极大似然估计的均方误差要小于矩估计的均方误差，所以极大似然估计法的估计效果比矩估计法要好。在两种极大似然估计算法中，后验的熵的极大似然估计的均方误差最小，说明其效果最优。

图2是四种算法下超熵He均方误差的比较。由图2可知，经典超熵的矩估计的均方误差最大，超熵的后验极大似然估计的均方误差最小，所以四种算法中超熵的后验极大似然估计算法效果最优。参数的矩估计随着样本量变化的增加波动较大，而极大似然估计的波动较为平缓，且极大似然估计的均方误差要小于矩估计的均方误差，所以极大似然估计法的估计效果比矩估计法要好。在两种极大似然估计算法中，后验的超熵的极大似然估计的均方误差最小，说明其效果最优。

图1 四种算法下熵En均方误差比较

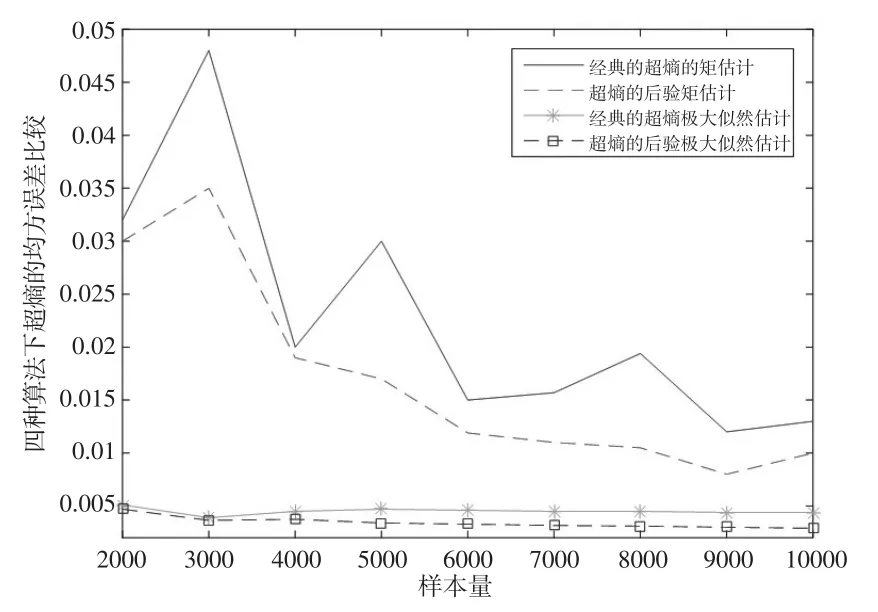
图2 四种算法下超熵He均方误差的比较

5 结束语

本文主要研究了云参数的估计方法，在经典参数估计的理论基础上，应用贝叶斯理论得到了后验的参数估计方法，并将经典的参数估计法与后验的参数估计法加以比较，得到了后验的极大似然估计效果最优的结论，所以在今后估计云参数时应使用后验的极大似然估计法以使云参数值更加准确。