基于矩阵分解的最近邻推荐系统及其应用

王 娟 ，熊 巍 ，b

（对外经济贸易大学a.统计学院;b.大数据风险与管理研究中心,北京 100029）

0 引言

随着互联网的日益发展，大数据逐渐进入人们的日常生活。海量数据的可获得性使人们获取信息更为便利，生活更加高效，但是在海量数据中也存在着大量的垃圾数据，对于用户来说，如何在这些数据中精准高效地找到自己需要的信息变得更加困难，开发高效推荐系统的需求更加强烈。同时大数据的可获得性产生了推荐系统的新问题——稀疏性，大规模的用户数据集与物品数据集可以获得，但是每个用户只对少量的物品做出评分，使得评分矩阵存在高度稀疏性，协同过滤及其他一些传统的推荐算法表现不佳。矩阵分解推荐算法在稀疏性与冷启动问题上都有很好的表现，目前的矩阵分解推荐算法有隐语义模型、奇异值分解、非负矩阵分解等，其主要原理是根据用户评分矩阵推断出用户和物品的隐语义向量，然后根据隐语义向量进行推荐。但矩阵分解有其弱点，就是解释性差，不能很好地为推荐结果做出解释；且矩阵分解并未考虑用户之间的相似性。本文创新性的将矩阵分解的结果应用于最近邻推荐算法，综合二者的优点预测推荐系统评分，并能很好地解释推荐结果。

利用Book-Crossing图书社区整理的278858个用户对271379本书进行的评分数据，显示评分仅有397243条，稀疏性达到99.9995%。针对稀疏矩阵首先进行了矩阵分解插值，然后利用基于用户的最近邻推荐算法寻找测试集用户的最近邻集合，并根据最近邻用户的评分作出推荐。该方法先考虑了用户与物品之间的联系，并解决了稀疏矩阵的问题，最近邻集合则考虑了用户之间的相似性，并能给出推荐结果的直观解释。综合矩阵分解与最近邻推荐算法的优势给出了更为有效的推荐算法。

1 文献综述

不同的推荐算法利用推荐系统中的不同信息给出推荐。基于内容的推荐算法考虑的是用户感兴趣的物品的特征相似度，选择与用户已评分项目有相似特征的项目推荐给用户。如Blancofernandez等（2008）[1]、Lops等（2011）[2]、Mooney和 Roy（2000）[3]、Pazzani和 Billsus（2007）[4]等都对基于内容的推荐系统进行了研究。Blancofernandez等（2008）[1]在分析项目之间的相似性时改进了句法相似性过度专门化的问题，Mooney和Roy（2000）[3]则运用了信息提取和机器学习算法对项目进行文本分类，提升了预测精度。基于用户的协同过滤考虑了用户之间的相似性，利用最近邻用户的评分预测目标用户的评分；基于项目的协同过滤则考虑了项目之间的相似性，该算法并未考虑项目的特征属性，其主要是根据用户的评分行为计算项目的相似度并给出推荐。Bell和Koren（2007）[5]改进了最近邻推荐中相似系数的权重计算方法，Koren（2010）[6]从评分矩阵出发提出了一种新的计算用户之间相似性的方法来改进协同过滤算法。在2009年的Netflix大赛上，Koren等（2009）[7]首次将矩阵分解应用于推荐系统，并在Movielens数据集上得到了很高的预测精度，有效地解决了评分矩阵稀疏的问题。矩阵分解推荐算法将原始的评分矩阵分解为用户-因子矩阵和项目-因子矩阵，可以有效地解决稀疏性与冷启动问题。目前的矩阵分解推荐算法有隐语义模型、奇异值分解、非负矩阵分解等，其主要原理是根据用户评分矩阵推断出用户和物品的隐语义向量，然后根据隐语义向量进行推荐，但矩阵分解的结果不易解释且没有考虑用户之间的相互影响。Cacheda和Formoso（2011）[8]的分析结果表明在稀疏条件下SVD明显好于其他一些传统的推荐算法；Nguyen和Zhu(2013)[9]也研究了矩阵分解算法，创新性地将项目的内容信息融入了矩阵分解算法中，内容增强的矩阵分解算法不仅提高了推荐的准确性，而且对内容提供了有用的见解，使推荐更易于解释。Wu(2007)[10]采用了三种不同类型的矩阵分解算法：规则化的矩阵分解、最大利润矩阵分解和非负矩阵分解，并将得到的结果与几个参数结合起来实现了一个比Netflix系统更好服务的推荐算法。在单一推荐算法的发展下，一些混合推荐算法开始逐步发展起来，混合算法可以充分考虑评分矩阵的多类问题（如稀疏性、冷启动）而给出更为精准的推荐。Melville等（2002）[11]将协同过滤与基于内容的推荐方法结合，使用基于内容的预测器来增强现有的用户数据，然后通过协同过滤提供个性化的建议，实验结果表明内容增强的协同过滤要比纯粹的协同过滤和一般的混合方法要好。

目前的研究集中于协同过滤与矩阵分解两大方向，协同过滤易于解释，且考虑了用户之间或用户与项目之间的相似性，但在稀疏条件下则表现不佳。矩阵分解可以有效解决矩阵稀疏问题，但是其分解的两个矩阵难以得到一个很好的解释。本文提出了基于矩阵分解的最近邻推荐算法，针对稀疏矩阵首先进行了矩阵分解插值，然后利用基于用户的协同过滤推荐算法寻找测试集用户的最近邻集合，利用最近邻用户的评分作出推荐，先考虑了用户与物品之间的联系，最近邻集合则考虑了用户之间的相似性。结合矩阵分解与协同过滤的优点预测推荐系统评分，能够很好地解释推荐结果并提高预测精度。

2 模型介绍

评分矩阵中普遍存在的情形是用户、项目数量都很大，但是用户只对部分项目有评分。用户-书籍评分矩阵中存在大量未评分数据，传统的基于项目的最近邻推荐与基于用户的最近邻推荐算法在稀疏矩阵中的表现黯然失色。

而矩阵分解算法的原理是：基于用户的行为对项目进行自动聚类，也就是把项目划分到不同类别/主题，这些主题/类别可以理解为用户的兴趣。对于一个用户来说，他们可能有不同的兴趣。例如用户A可能喜欢文学作品、语言学，用户B可能喜欢文学、经济与资讯类，用户C可能喜欢军事、历史等，基于这样的想法，单纯对书籍的分类可能并不能反映用户的兴趣所在。本文在可见的书籍名单中归结出几个类别，不等于该用户就只喜欢这几类，对其他类别的书籍就一点兴趣也没有。也就是说，本文需要了解用户对于所有类别的兴趣度。对于一个给定的类来说，需要确定这个类中每本书籍属于该类别的权重。权重有助于确定该推荐哪些书籍给用户。

假设评分矩阵为Rn*m，分解为两个矩阵Pn*k，Qk*m的乘积：

矩阵值Rij表示的是用户i对项目j的兴趣度。将R矩阵表示为P矩阵和Q矩阵相乘。其中P矩阵是用户-类别矩阵，矩阵值Pik表示的是用户i对类别k的兴趣度；Q矩阵是类别-项目矩阵，矩阵值Qkj表示项目j在类别k中的权重，权重越高越能作为该类的代表。然后根据如下公式来计算用户i对项目j的兴趣度：

防止过拟合，引入正则化后的目标函数为：

采用随机梯度下降法求解该最优目标：

更新的Pik，Qkj为：

对于一个用户来说，当计算出他对所有项目的兴趣度后，就可以对评分矩阵插值。矩阵分解算法从数据集中抽取出若干潜在因子，作为用户和项目之间连接的桥梁。

利用矩阵分解算法估计出每个用户未评分项目的潜在评分，在这个过程中主要考虑了用户与项目之间的作用关系，然后对插值后的评分矩阵进行中心化。

在中心化后的评分记录中找出测试集用户u的最邻近用户集，充分考虑用户之间的相似性。计算最近邻集合中对每个项目的加权评分，计算估计误差。

采用余弦相似度计算相似性：

目标用户u相似矩阵为：

根据用户相似矩阵寻找与目标用u相似的k个用户构成最近邻集合。

用户u对项目j的预测评分为：

根据用户u对所有项目的预测评分计算预测误差，评估模型预测精度。

优点：先利用矩阵分解寻找用户与项目之间作用关系，通过提取项目的不同属性，以及用户对不用属性的兴趣度，计算用户对该项目的整体兴趣度作为第一步得出插值，再利用用户之间的相似性找出目标用户的最近邻集合，利用最近邻集合的加权评分作为目标用户对于项目的预测评分。在这个模型分析中，从用户与项目之间的相关性及用户之间的相似性两个维度出发预测评分，充分利用了评分矩阵中的信息。

3 书籍评分数据分析

本文通过book-crossing数据集来验证所提出的基于矩阵分解的协同过滤算法的推荐效率，Book-Crossing图书社区收集了278858个用户对271379本书的评分，包括显式和隐式的评分。评分记录共计1048575条，其中显式评分有397243条，评分范围为1～10，1分表示极不满意，10分表示很满意。隐式评分有651332条，用0表示，隐式评分是指用户的浏览购买记录，一般用0和1表示，0表示没有浏览/购买，1表示浏览/购买。如果用户浏览过，但是没有给出评分，可以推断他不喜欢该项目，而没有浏览过只能表明用户暂时没有接触过这个项目。本文的实证部分采取显式评分进行分析。Book-Crossing数据包括三个数据集；用户信息集包括用户ID、年龄、所在国家、州等人口统计学属性；书籍信息集包括书籍ISDN编码、书籍名称、作者、出版社、出版年份信息；还有用户评分数据集。原始数据中存在部分无效数据，首先要对数据进行一系列预处理。

3.1 数据处理

考虑到数据过于稀疏，在本文的分析中，首先对数据进行了统计，只选取评分书籍不小于20本的用户以及评分用户不小于20个的书籍，筛选过后的用户共计2789名，书籍总数达到1846本。评分记录共计38854条，数据稀疏性为99.25%。从评分记录中随机抽取1000条记录作为测试集。评分记录如表1所示。

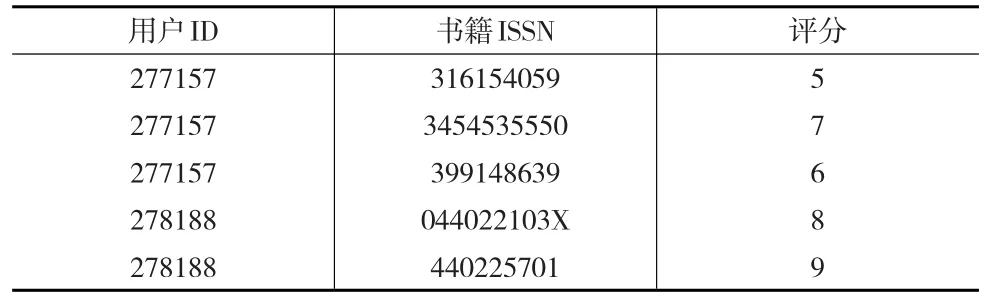
表1 部分评分记录

图1展示了各类评分数据频率分布，从图1可知，评分矩阵中用户倾向于给出较高的分数，评分众数和中位数均为8，平均评分为7.94。

图1 评分数据分布柱形图

图2给出了用户累积评分分布折线图，对用户评分频率降序累积排列并画出折线图，评分最多的用户做出了913个评分，大约483个用户评分数据占到了所有评分数据的50%。

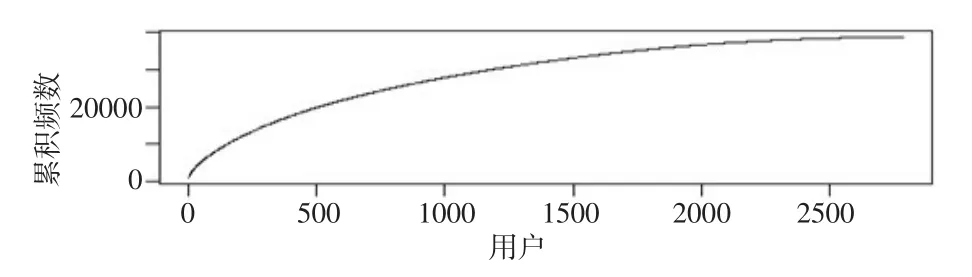
图2 用户累积评分分布折线图

图3给出了书籍累积评分分布折线图，从书籍累积评分来看，评分最多的书籍有221个用户评分，大约对于470本书的评分个数即达到了整体评分数的50%。

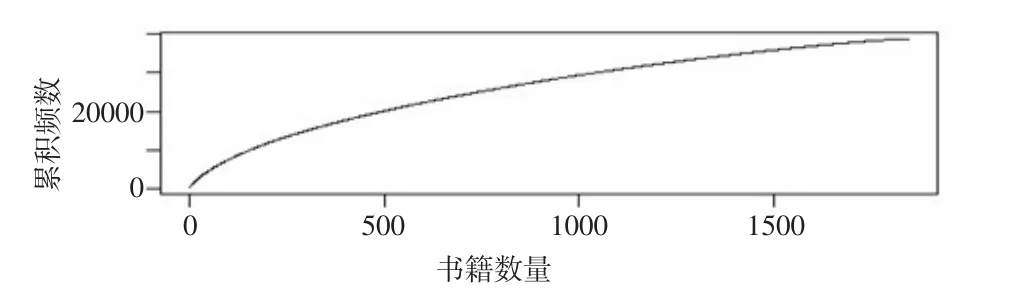
图3 书籍累积评分分布折线图

3.2 误差衡量标准

推荐系统常用的误差衡量指标有均方误差（RMSE）、平均绝对误差（MAE）。测试集共1000个数据。

在矩阵分解后得到矩阵R=P*Q,然后基于最近邻集合计算测试集用户的预测评分，填补评分矩阵的缺失值，计算测试集的误差。

3.3 基于矩阵分解的最近邻推荐系统

矩阵分解得到的R矩阵对评分矩阵插值填补，然后对1000条测试集记录做中心化。

寻找测试集1000条记录对应用户的10个最近邻集合，利用相似系数加权计算目标用户已评分项目的预测评分并计算预测误差RMSE和MAE。表2为矩阵分解过程中所用参数。

表2 梯度下降法求解矩阵分解中的参数设置

表3（见下页）为不同矩阵分解主题下的MF-CF方法的预测误差。由表3可知，随着k值的增加，预测误差首先表现为逐渐减小，当k值大于30以后，预测误差不再减小，并会随着k值的增大出现小幅增加。当k值为30时，MF-CF预测方法的平均绝对误差为0.74，回顾原始数据评分为1～10，间距较大，其平均预测误差较小，预测变化较小，表明了MF-CF方法在Book-Crossing数据集上得到了较为合理的结果。

4 结论

本文首先对稀疏矩阵做了矩阵分解，并用梯度下降法求出对应的P、Q矩阵，从用户对项目的偏好角度预测用户评分，然后利用已插值的评分矩阵计算目标用户的最近邻集合，并利用最近邻用户的评分预测目标用户的评分。在模型估计部分计算了不同k值下的矩阵分解的误差，并选取了最优的k值进行预测。

本文只是从稀疏矩阵出发对分层混合推荐方法的一个尝试，在混合推荐算法的具体应用中，还有较多的算法未能应用在此与文中算法进行对比。从数据来看，本文所设计的数据只是对原始数据中显式评分数据的建模，原始数据中包含有大量的隐式评分并未在该方法中考虑，在以后的分析中可以应用隐式评分对Book-Crossing完整数据集进行分析。作为该想法的扩展研究，原始数据集中还包括了用户的一些基本人口统计学信息及书籍的基本信息，利用数据挖掘和文本分析等方法充分利用这些信息提高推荐系统的质量也是继续深入研究的一个方向。

表3 不同参数下推荐性能比较