具有恐惧效应和食饵避难所的Leslie - Gower捕食者食饵模型的动力学分析

刘英姿, 李忠, 何梦昕

( 1.福州大学 数学与统计学院, 福州 350108; 2.闽江学院 数学与数据科学学院, 福州 350108 )

0 引言

捕食者- 食饵模型是描述种群关系的一个重要模型.研究发现，捕食者的存在会改变食饵自身的生理机能,例如食饵会因为担心被捕食者而降低自身的繁殖能力或改变栖息地,学者们将这种现象称为恐惧效应[1].2016年, Wang等[2]首次将恐惧效应考虑到捕食者- 食饵模型中,研究显示较大的恐惧可以促进系统的稳定.2017年, Sasmal[3]提出了一种具有恐惧效应和Allee效应的捕食者- 食饵模型,研究显示该模型会使系统产生双稳现象.2019年, Zhang等[4]提出了一种将恐惧效应和避难所相结合的捕食者- 食饵模型,研究发现恐惧效应和避难所会改变食饵和捕食者的种群密度,同时恐惧效应也会促进系统的稳定.2020年, Wang等[5]讨论了一种具有恐惧效应的Leslie - Gower捕食者- 食饵模型,并分析了该系统的稳定性和Hopf分支.基于上述研究,本文研究如下具有恐惧效应和食饵避难所的Leslie - Gower捕食者- 食饵模型的动力学行为:

(1)

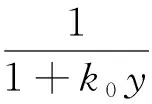
(2)

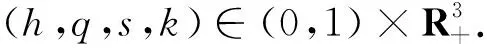
1 预备定理

定义系统(2)的初值条件满足x>0,y≥0, 则由此易得正y轴是系统(2)的不变集,且系统(2)的解都是正的.

定理1系统(2)的解是有界的.

由于原点在系统(2)的右端没有意义,无法通过雅克比矩阵分析原点的稳定性,所以本文利用吹胀方法来讨论原点的稳定性.

定理2系统(2)的原点是一个不稳定的点.

证明利用水平吹胀的方法令x=u和y=uv,则系统(2)可变为如下系统:

(3)

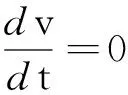
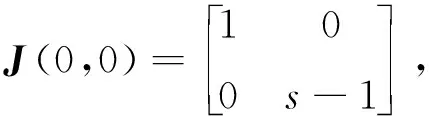
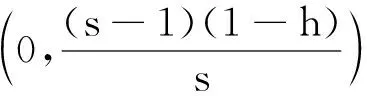
其中P(u,v)和Q(u,v)是不低于3次的解析函数.利用文献[6]中的定理7.1进行判定可知,当s=1时由系统(2)的原点吹胀出来的点(0,0)是一个排斥的鞍结点.再利用垂直吹胀的方法即令x=ηw,y=η和dt=(1-h)dτ(仍然用t表示τ),则系统(2)可变为如下系统:

(4)

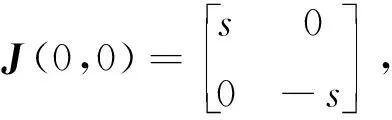
2 平衡点的稳定性

(5)

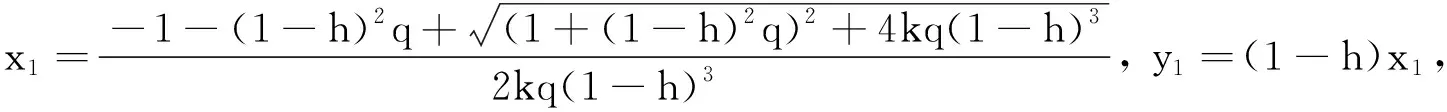
定理3系统(2)的边界平衡点E0是一个鞍点.

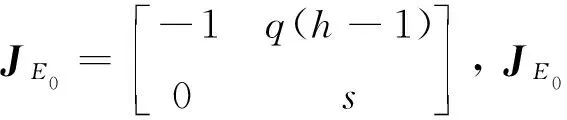
定理4系统(2)的正平衡点E1是局部渐近稳定的.

证明系统(2)在E1点的雅可比矩阵JE1及其行列式和迹分别为:

由以上易知Det(JE1)>0, Tr(JE1)<0, 所以正平衡点E1是局部渐近稳定的,证毕.

定理5系统(2)的唯一正平衡点E1是全局渐近稳定的.

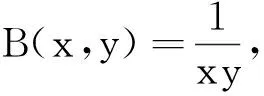
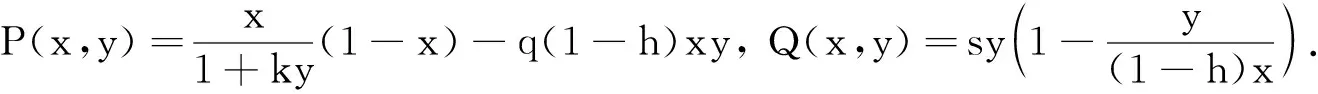
3 恐惧效应和食饵避难所对种群密度的影响

正平衡点E1(x1,y1)满足如下方程:

(6)

利用隐函数求导法则求x1和y1对k的导函数可得:

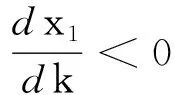
下面讨论食饵避难所对食饵和捕食者种群密度的影响.利用隐函数求导法则求x1和y1对h的导函数可得:

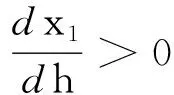
下面用两个例子来分别说明恐惧效应和食饵避难所对种群密度的影响.

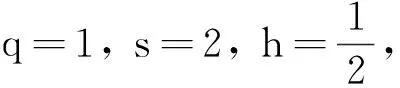
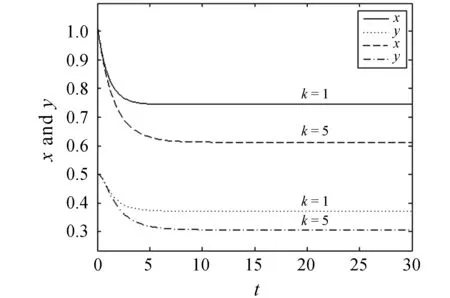
图1 恐惧效应对种群密度的影响

(7)

取k=1, 则系统(7)的唯一正平衡点为E1(0.745,0.372); 若取k=5, 则系统(7)的唯一正平衡点为E1(0.612,0.306).图1为恐惧效应对种群密度的影响.由图1可以看出,随着k值的增大,食饵和捕食者最终均达到稳定的种群密度(分别由0.745降到0.612, 由0.372降到0.306), 由此可知恐惧效应不利于食饵和捕食者种群密度的增加.

例2对系统(2)取参数k=1,s=2,q=4,即考虑如下的系统:

图2为食饵避难所对食饵种群密度的影响.由图2可以看出,食饵的种群密度随着避难所h的增大而增大,说明增加食饵避难所有利于食饵种群密度的增加.图3是食饵避难所对捕食者种群密度的影响.从图3可以看出，当h的取值为00.548), 较多的食饵会进入避难所,因此此时捕食者能够捕获的食饵变少,即较大的食饵避难所不利于捕食者种群密度的增加.

图2 食饵避难所对食饵种群密度的影响 图3 食饵避难所对捕食者种群密度的影响

4 结论

本文考虑了一类具有恐惧效应和食饵避难所的Leslie - Gower捕食者-食饵系统,证明了该系统具有唯一的正平衡点，且该点是全局渐近稳定的.研究还表明：恐惧效应和食饵避难所对系统的稳定性没有影响,但是恐惧效应和食饵避难所会改变食饵和捕食者的种群密度.其中恐惧效应会降低食饵和捕食者的种群密度，食饵避难所会增加食饵的种群密度,较小的食饵避难所会增加捕食者的种群密度,较大的食饵避难所会降低捕食者的种群密度.该结果可为调整种群密度提供参考.本文模型考虑的是相对简单的Holling I型功能性反应函数,在今后的研究中我们将考虑一些更为复杂的功能性反应函数,以此进一步研究具有恐惧效应和食饵避难所的捕食者-食饵模型的动力学行为.