基于自动机的用户名合法性检测方法
刘帆, 赵亚慧,, 崔荣一
( 1.延边大学 融合学院, 吉林 延吉 133002; 2.延边大学 工学院, 吉林 延吉 133002 )
0 引言
用户名合法性检测问题的本质是字符串匹配问题.与传统的字符串匹配不同,合法性检测问题只需保证字符类别匹配成功即可.合法的用户名字符串需同时含有数字、特殊字符、大写字母且其长度需大于8位.传统的字符匹配算法主要有暴力匹配(BF)算法[1]、Rabin - Karp(RK)算法[2]、字符串查找(KMP)算法[3]以及正则表达式[4].其中: BF算法虽然简单,但耗时较大; RK算法是基于哈希函数的一种对BF算法改进的算法,在正常情况下该算法的效率虽然优于BF算法,但当哈希产生冲突时该算法的效率仍然较低; KMP算法是一种采用消除主串指针回溯的方法对BF算法进行优化的算法,该算法虽然能够弥补BF算法在主针回溯后需重新开始进行比较的缺点,但在重复率很高的文本中其效率低于BF算法;正则表达式与上述方法相比,虽然时间效率有所提高,但存在空间复杂度高和易出错等缺点[5].近年来,一些研究者基于上述方法又提出了BM算法[6]和Sunday算法[7],这两种方法虽大幅提高了字符串匹配的效率,但二者过于依赖于辅助数据结构,且预处理时间过长.
1956年, Moore等首次提出了有限状态自动机的概念[8],并在后续的研究中针对字符串匹配问题提出了有限状态自动机算法—Aho - Corasick(AC)算法[9].该算法与上述传统算法相比,只需扫描一遍字符串即可,且其时间复杂度与模式串的规模无关,因此该算法受到学者们的关注.目前利用该方法虽然可以检测用户名字符串中包含的类别,但无法检测用户名长度,因此其应用性受到一定限制.为此,本文提出了一种新有限状态自动机,并通过分析验证了该自动机的有效性.
1 有限状态自动机
传统的有限状态自动机由一个五元组组成[10]:
M=(Q,Σ,δ,q0,F).
(1)
其中:Q是包含自动机中所有状态的非空集合;Σ是字母表,自动机接收的任意字符均为该集合元素;δ是状态转移函数,其中δ:Q×Σ→Q, 对∀(q,a)∈Q×Σ, ∃p∈Q有δ(q,a)=p,它表示自动机M在状态q时读入字符a之后,状态q随即转向状态p;q0为M的初始状态,q0∈Q;F为终止状态集合,F⊆Q,∀q∈F,q称为M的一个终态.
对于∀x∈Σ*, 若有δ(q0,x)∈F, 则称x被M所接受;对于∀x∈Σ*, 若有δ(q0,x)∉F, 则称x不被M所接受[11].所有可以被M接受的x的集合称为M可接受的语言,表示为:
L(M)={x|x∈Σ*且δ(q0,x)∈F}.
(2)
假设Q={q0,q1,q2},Σ={0,1},F={q2},δ(q0,0)=q1,δ(q0,1)=q0,δ(q1,0)=q2,δ(q1,1)=q0,δ(q2,0)=q2,δ(q2,1)=q0, 则此时的自动机M如图1所示,其状态转移函数如表1所示.在图1中,单圆圈代表自动机中的中间状态,双圆圈代表终止状态,标有字符的有向箭头代表转移函数,箭头S所指向的单圆圈代表初始状态.

图1 M的状态转移图

表1 M的状态转移函数
2 自动机模型的构建
为了便于检测用户名的合法性,本文设计了一种可计数的有限状态自动机,其检测流程如下:①用户提交需检测的用户名.②系统利用同态映射对用户名进行字符分类(属于同一类的字符被映射为同一个字符,同时用户名字符串映射为对应类别字符串);若某类别字符串可以被该自动机正确识别,则对应的用户名字符串为合法,否则为不合法.由于自动机每次只能输出一个字符,不能直接输出用户名是否合法,因此本文设计了一个解码函数.该解码函数可根据自动机最后的状态输出用户名不合法的原因.用户名映射、自动机识别以及状态解码的过程如图2所示.

图2 用户名映射、自动机识别和状态解码的过程
2.1 映射函数和解码函数
用户名字符分类是一个同态映射过程.设D是初始用户名字符串,E是分类字符串,f:D→E为映射,对于∀d1,d2∈D有f(d1d2)=f(d1)f(d2), 则称f是D到E的同态映射.本文将用户名字符分类的映射函数定义为:

(3)
其中x是原始用户名字符串中的字符.
输出不合法原因的解码函数是一个映射过程,即当∀a∈A,∃b∈B, 且有h(a)=b, 称h是A到B的映射.本文将解码函数定义为:
(4)
其中,x是指自动机在接收一个字符串后跳转到的最终状态.
2.2 自动机模型的构建
本文建立的自动机模型G由一个六元组组成:
G=(Q,Σ,δ,q0,F,n).
(5)
其中:Q、Σ、δ、q0、F与有限状态自动机的定义一致;n为计数器(自动机每接受1个字符时,n减1).G的状态转移函数如表2所示.本文算法的具体步骤如下:
输入:字符串s
输出:用户名是否合法
Step 1 对字符串s进行映射,得到映射串s′;
Step 2 根据状态转移函数表初始化状态转移字典trans, 同时将n初始化为8;
Step 3 设初始状态为q0, 即设待匹配字符串的首位为i=0;

表2 G的状态转移函数
Step 4 读完字符串时,若n≤0时则算法结束,否则跳转到Step 5;
Step 5 依据最终状态进行解码并输出字符中不合法的原因,算法结束.
该算法中,输入是需验证合法性的原始用户名s; 输出是该用户名s是否合法.若合法,不输出错误;若不合法,输出不合法并给出原因.映射串s′是输入字符串s经函数f(x)同态映射得到的分类字符串,字典trans是依据表2进行初始化的状态转移函数,n赋值为8表示合法用户名至少是9位字符;end表示自动机为终态,end∈F.
3 算法分析
3.1 算法有效性证明
对于任意的一个输入字符串a1a2…an, 根据文献[10]中的定理1可知:对于∀q∈Q,ω∈Σ*,a∈Σ, 有δ(q,wa)=δ(δ(q,w),a).由此可得:
δ(q0,a1a2…an)=δ(δ(q0,a1a2…an -1),an)=δ(δ(…δ(q0,a1)…),an).
(6)
再根据表2可得:
δ(q0,a1a2…an)=δ(δ(q0,a1a2…an -1),an)=δ(δ(…δ(q0,a1)…),an)=end.
(7)
依据计数器的定义,此时接收到的字符串a1a2…an的值为:
n=8-|a1a2…an|.
(8)
公式(8)中的|a1a2…an|表示字符串a1a2…an的长度.当式(8)中求得的n大于0时,自动机在end(终态)处跳转至下一状态,即表示用户名不合法.因此,只有当自动机最后到达的状态是终态时,该用户名才是合法的,否则为不合法.根据本文算法构造的用于检验用户名合法性的可计数自动机如图3所示.
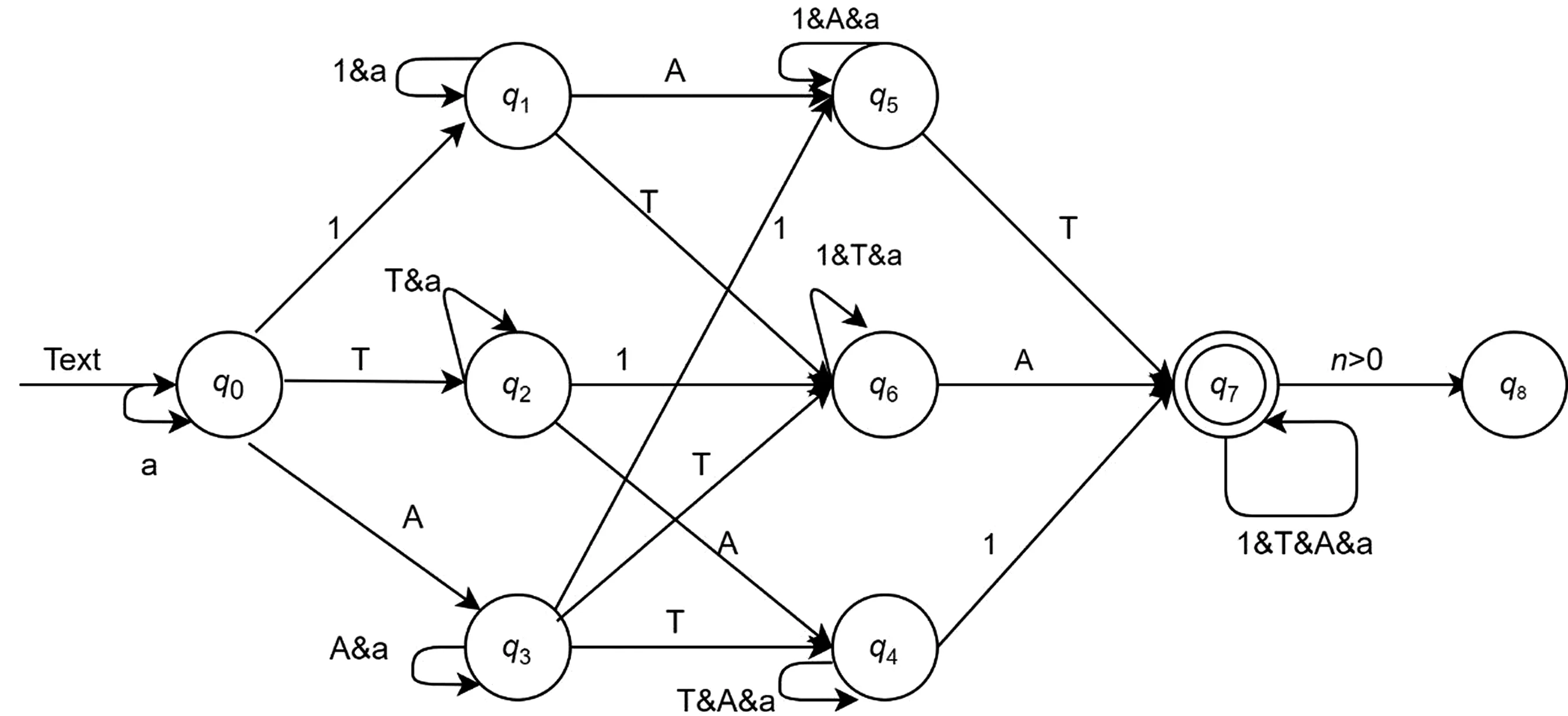
图3 可计数自动机的状态转移图
本文以输入字符串s和t为例验证本文构造的自动机的有效性,其中假设s为‘abA*’和t为‘2B&’, 映射串s1(‘aaAT’)和t1(‘1AT’)由s和t经映射函数f(x)得到.图4和图5分别是s1和t1的状态转移图,图中的虚线为字符串在自动机中的转移路线.由图可知,s1和t1经自动机转移到的最终状态分别是q4和q8.由于q4和q8均不是终态,因此这两个字符串是不合法的.此时解码函数h(x)输出的是:“该用户名缺少数字,不合法”和“该用户名长度不够,不合法”.上述实例证明本文提出的算法可以有效验证用户名的合法性,且具有简单、稳定的优点.

图4 s1的状态转移图
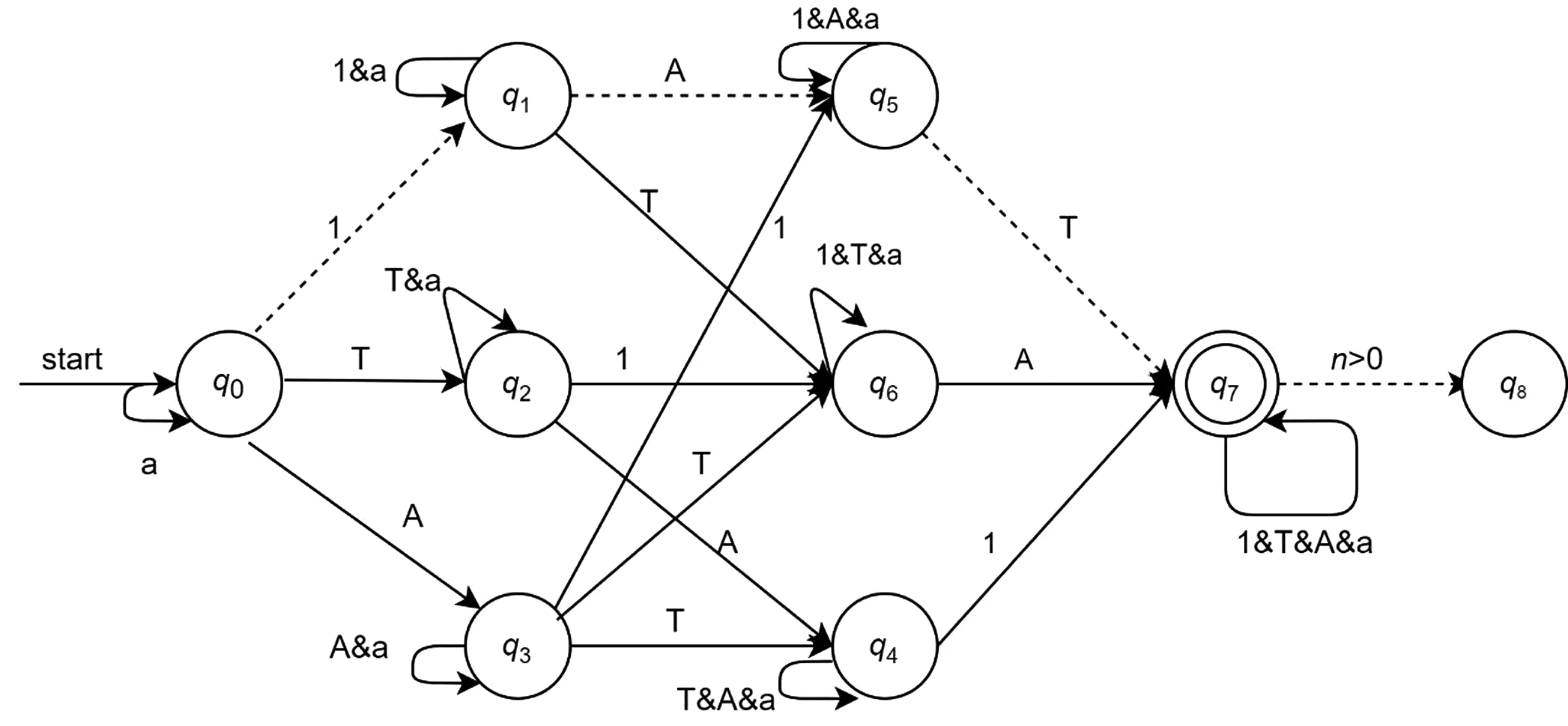
图5 t1的状态转移图
3.2 算法复杂度分析
表3为传统有限自动机模型(DFA)与本文所提模型(N - DFA)的复杂度,其中n为需要满足的条件个数,m为用户名长度.由表3可知,本文所提模型在时间复杂度和空间复杂度方面均优于传统模型.

表3 不同模型的复杂度
4 结论
研究表明,本文设计的模型可实现有限状态自动机的计数和设置输入字符串的长度,且具有检测效率高、性能稳定等优点,因此本文方法可用于用户名的合法性检验.本文算法未能实现计数器和终态的完全分离,拟在今后的研究中通过调整计数器和终态的关系使二者相互独立,以使本文算法达到更好的检测效果.

