冯诺依曼型元胞自动机和自指语句
邬舒雯 熊明
1 引言
元胞自动机(Cellular Automata,CA)是一类时间和空间离散的数学系统,其特征是局部相互作用和内在的并行演化形式。元胞自动机这一概念起源于冯诺依曼(von Neumann)在“自动机的一般逻辑理论”(The General and Logical Theory of Automata)中所提出的二维自复制自动机系统。(参见[12])元胞自动机结构、规则简单,但能产生复杂的行为模式,因此作为一类复杂系统的最简单数学表示,被广泛应用于交通运输、计算机科学、人工智能、生物科学、物理学等众多学科领域。
近年来,文[9]提出了能够将元胞自动机与自指语句相联系的观点。文中提出元胞自动机的演化过程与自指语句的修正过程这两个动态过程在本质上是相同的,这种相似性,使我们能够将元胞自动机和自指语句,一个属于计算机科学和一个属于逻辑学的两个不同研究领域的理论概念相互联系起来进行研究。文[9]主要研究了初等元胞自动机及其相关联的自指语句,从初等元胞自动机诱导出若干类悖论,并根据自指语句的特征对初等元胞自动机给出了一个分类。
文[9]用来分析自指语句的一个关键概念是修正序列,这是来自于修正理论(参见[5,6])的基本概念。在这个理论中,自指语句分阶段按照修正规则与极限规则进行赋值,每个语句都可建立一个动态的赋值过程,这样的过程即为修正过程。本文基于文[9]提出的理论,将目光投向到更为复杂的二维元胞自动机系统中,研究一类特殊的冯诺依曼型元胞自动机及其相关的自指语句。我们尝试从前者给出一些悖论,并对此类冯诺依曼型元胞自动机在演化过程方面的特征进行逻辑学视角的分析。
本文采用文[9]中表达自指语句的形式语言,即带有一元谓词符号T的一阶算术语言(LT)。对此语言中的语句的哥德尔数同时也表示对应的数字符。因而,当T表示真谓词时的意思是C是真的。
本文结构如下:第二节将介绍文[9]在初等元胞自动机与自指语句的主要思想,为本文的分析奠定理论依据;第三节引入冯诺依曼型元胞自动机的基本概念,并给出对应的自指语句的表达方式;第四节根据[9]提出的方法,给出寻找此类元胞自动机演化过程中不动点的方法。然后,第五节将进一步对冯诺依曼型元胞自动机不动点的表现性质进行分析,并通过引入说谎者悖论的相关性质进行比较,最后一节将总结前面所做的相关内容,并尝试给出一种冯诺依曼型元胞自动机的分类。
2 初等元胞自动机和自指语句
元胞自动机是由无数个排列在网格结构的具有自身状态值的元胞构成,每个元胞的状态值都是根据一组明确的规则随时间的变化确定性地演变,并且这些规则涉及相邻元胞的状态值。在数学上,常把元胞自动机表示为由元胞状态、邻域和演化规则构成的三元组〈S,r,f〉,其中S是状态的有限集,r是邻域的半径,f是迭代函数(也称为局部函数)。
作为元胞自动机的基本单位,元胞分布在一定维数的空间网格中,此网络结构可向各个维度无限延展而形成所谓的“元胞空间”。根据元胞空间的维数,元胞自动机可以划分一维、二维及更高维的元胞自动机。如果把一维元胞自动机看作是元胞在一条带子上进行演化的自动机,那么二维的元胞在一个平面上进行演化的自动机。在前一类中,领域半径为1 且状态集为{0,1}最为简单且基本,被称为初等元胞自动机,它与自指语句之关联是本文研究之基础。在后一类中,则有本文将详加研究的Totalistic 的冯诺依曼型(von Neuman Neighborhoods)元胞自动机1除冯诺依曼型外,二维中典型者还有摩尔型(Moore Neighborhoods),广为人知的康威(John Conway)生命游戏就是属于摩尔型,详情参见[4]。,其解释见下一节。
本节主要解释初等元胞自动机与自指语句如何发生关联。初等元胞自动机中的元胞均匀地分布在一条两段可无限延伸的带子上,因此每个格子以由整数索引:Ci,i ∈Z。在每个离散时间阶段‘t’,元胞Ci在t阶段的状态Ci(t)必为布尔值0和1(图示用白格和黑格表示)之一。Ci的两个最近的邻居表示为Ci-1(左邻居)和Ci+1(右邻居)。Ci在t+1 阶段的状态由它与它的两个邻居在步长t的状态决定。决定方式由演化规则(或迭代函数)来规定。例如,图2-1 给出了一种演化规则。在一定的初始状态下,每个格子的演化是唯一确定的。因此,可用不同的演化规则来区分不同的元胞自动机。图2-1 对应的自动机被命名为ECA 452文[1]中使用“ECA n”(或“规则n”)来表示一个Wolfram 数为n 的初等元胞自动机。Wolfram 数是指根据Wolfram 给出的编码规则对元胞自动机进行编码所得的数字,详情参见[14],第65 页。。
每个演化规则本质上是一个有三个变元的布尔函数。例如,图2-1 实则是一个三变元的真值表,它正是ECA 45 的迭代函数f的表格表示。f(x,y,z)的布尔表达式为x⊕(y ∨¬z)。由此,ECA 45 的演化可由公式Ci(t+1)=Ci-1(t)⊕(Ci(t)∨¬Ci+1(t))3详情可参见https://www.wolframalpha.com/input/?i=rule+45,该网站给出了所有初等元胞自动机对应的布尔表达式。确定。
正如前文提到,文[9]把初等元胞自动机关联到自指语句。基本的思想是,对于每个初等元胞自动机,若其演化式为,则可定义自指语句的无限集{Ci|i ∈Z},其中,这里每个Ci不再表示格子,而是一个语句,它所断定者正是语句Ci-1,Ci,Ci+1按f组合的那种真值情况。例如,ECA 45 的对应的自指语句中,每个都断定要么语句Ci-1为真,要么或者语句Ci为真,或者语句Ci+1不为真。需要说明的是,元胞自动机的演化式可表达为布尔表达式对于当前的研究颇为重要,因为当前之研究与自指语句密不可分,而自指语句的表达必须借助布尔公式。布尔表达式对初等元胞机顺理成章,但对其他却未必,这一点在下一节将会显现出来。
初等元胞自动机与对应的自指语句的一个基本关联是:前者的演化过程与后者的所谓修正过程本质上是相同的。给定带子中每个元胞的初始状态,则每个初等元胞自动机在每个时间步长都唯一地给出每个元胞的状态,各个时间步长的状态演变就构成了一个演化过程。而修正过程来自于一个称为语义真理论的逻辑学领域,其中T预设的表示是真谓词“是真的”,其外延也按照一定的过程来演化,过程中每个阶段的外延都由上一阶段为真的语句构成。在此演化中,语句,尤其是上面提到的那些自指语句,因其表达式中含有T,其真值会随着阶段的改变而发生改变。这样,在此过程中,自动机中每个元胞对应的语句的真值也形成了一个演化过程,此演化过程被称为修正过程。(参见[5,6])
关于初等元胞自动机的演化过程和对应自指语句的修正过程以及这两种过程如何对应,具体细节可参见[9]。后面的讨论将直接利用初等元胞自动机上已经建立的一些事实,我们将把二维的元胞自动机的演化过程与对应的自指语句的修正过程也视为等同的。因此,正如[1]已经证明的那样,对任意初等元胞自动机,其对应的自指语句集是悖论的,当且仅当此自动机的演化过程没有不动点。对于二维的自动机,当知道其演化过程没有不动点,我们将直接指出其所对应的自指语句集也是悖论的4不动点之规定将在节5 针对二维情况给出规定,悖论语句的修正过程定义来自于[5,6],可参见[9]。。
3 冯诺依曼型元胞自动机的逻辑表达式
冯诺依曼型元胞自动机作为二维元胞自动机中常见的一种类型,是指元胞领域是包含目标元胞周围(上下左右)四个正交元胞的集合。我们可用矩阵形式表示冯诺依曼型元胞自动机,其中元胞是均匀排列的,并由整数索引:Ci,j,i,j ∈Z。由Ci,j+1,Ci,j-1,Ci-1,j,Ci+1,j表示目标元胞上下左右四个邻居。在每个离散时间阶段t,我们使用表示元胞Ci,j在阶段t的状态,由Ci,j表示的t阶段的结构是一个无限矩阵序列。本文研究状态集为{1,0}(分别通过黑白格子表示),领域半径为1 的最基础的Totalistic 规则(总和型),其解释形式可表示为:

目标元胞的状态是根据迭代规则和其邻域元胞状态随时间变化的。我们用颜色的从浅到深来分别对应f从0 到5 的值,用tn(tn ∈{0,1})表示在时间‘t+1’下相应的子规则Tn决定的目标元胞的值,可将T 型元胞自动机规则进行图示化,如图3-1 所示5所有此类规则图示都由电脑软件Wolfram Mathematica 12 绘制而成,不再进行一一说明。的冯诺依曼型元胞自动机(下文简称T 型元胞自动机)。同时,根据Wolfram 提出的编码规则,我们也可以对其进行相应的编码t5·25+t4·24+…+t0·20,所得的编码数也称为Wolfram 数。因此,我们共有26个T 型元胞自动机,用“Rn”(或“规则n”)来表示一个Wolfram 数为n的自动机。
为了更好地对T 型元胞自动机进行研究,我们需要将其演化规则进行形式化表达,代数表达式是其迭代函数最简单的表现形式之一。例,R31 元胞自动机的代数表达式为:


图3-1:冯诺依曼型元胞自动机的迭代规则
显然,用代数表达式可以直接表示T 型元胞自动机的迭代函数,但在逻辑语言中不使用加法,因此这种形式化表达方式不能直接地与逻辑自指语句联系起来。所以,需要进一步将其转化为逻辑符号进行表示。由上文我们已经知道对初等元胞自动机演化规则编写对应的布尔函数的值再进行简单的合取(或析取),就可以得到相应的自指语句形式,如ECA 45 的逻辑表达式。因此,我们对每一条T 型元胞自动机的子规则Tn编写相应的布尔函数的值,从而试图将自动机的迭代函数用逻辑表达式进行表达。
由(1)式已知,每个目标元胞的“t+1”状态值是由“t”状态下包括目标元胞在内的周边共五个元胞的值共同决定的。因为本文研究的是状态值为{0,1}布尔值的T 型元胞自动机且f ∈[0,5],因此可得决定元胞状况的子规则的情形由25种情形构成。由图3-1 可知,T1规则下包含5 种情形,而每一个Tn规则将分别有其相对应的情形。对此,我们假设所求迭代函数的逻辑表达式为A(表3-1 中A为R31 对应下的取值,后文中将进一步说明),对决定A所有可能值的情况如表3-1 所列。
如表3-1 所示,我们对满足Totalistic 规则的迭代函数的每种相应可能情形进行编码,从而将其对应到每一条Tn规则下:显然,T0规则只对应着1 情形;T1规则分别对应着2、3、5、9、17 情形;T2规则对应4、6、7、10、11、13、18、19、21、25 情形;T3规则对应8、12、14、15、20、22、23、26、27、29;T4规则对应16、24、28、30、31 情形;T5规则对应32 情形。每个T 型元胞自动机由每条子规则Tn共同决定,而每条Tn规则则能够给上述真值表赋予相对应的真值。因此,我们可以根据元胞自动机的演化规则所知道的A值,反解真值表,从而得到每个Totalistic 规则的逻辑表达式。
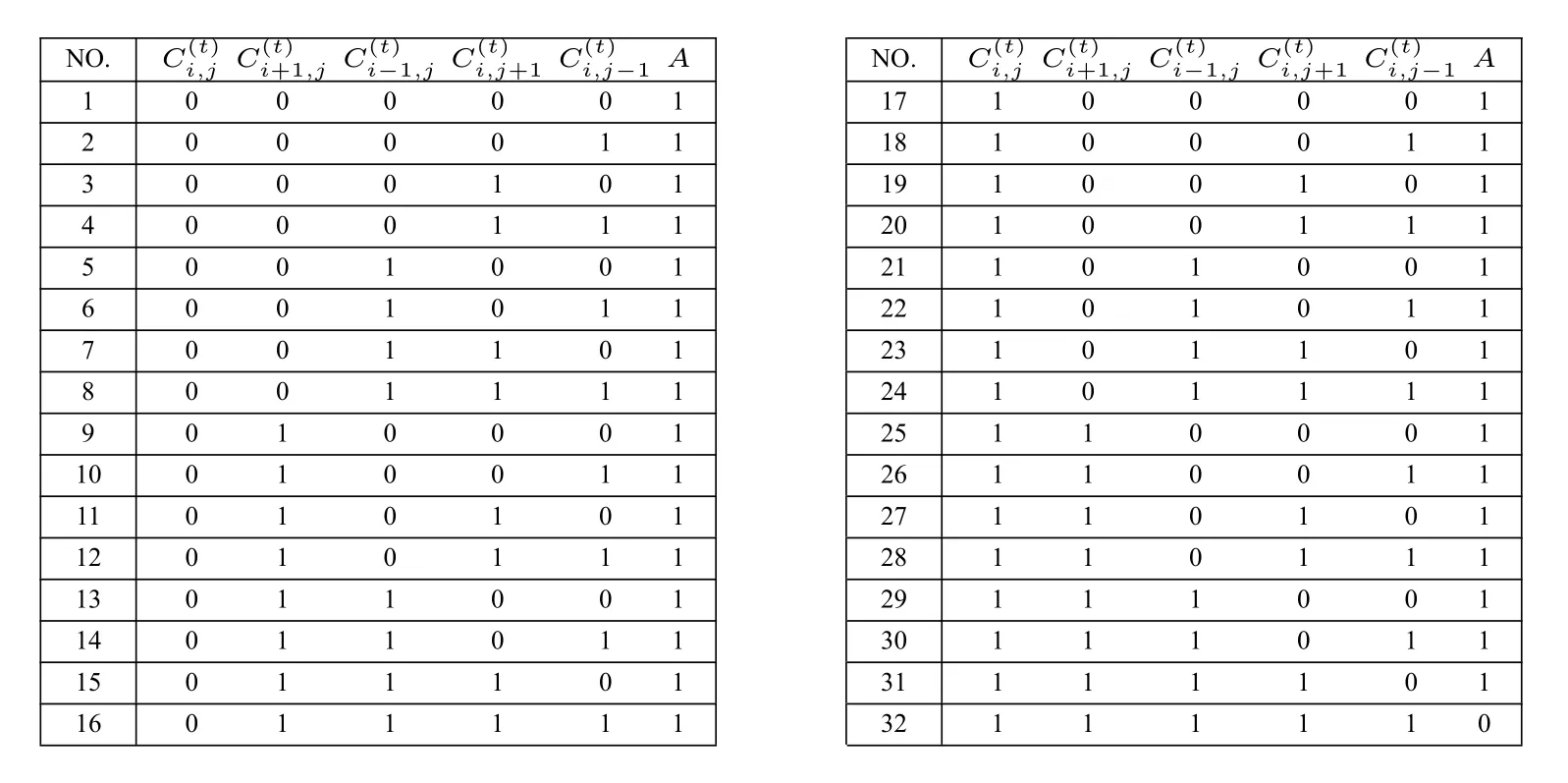
表3-1:决定逻辑表达式A 的所有真值表达形式

图3-2:冯诺依曼型元胞自动机R31 的迭代规则
让我们以R31 元胞自动机为例,说明根据真值表3-1 如何求得其逻辑表达式。R31 的T 型元胞自动机演化规则如图3-2 所示,有且仅有t5=0,因此我们可得A的取值如表3-1 所示。由表可得,仅有在32 情形下,A的值为0,因此根据该真值表求解可得A的逻辑表达式如下:

因为在R32 规则下A的值为0 的情形较少,为了简洁,我们可采取对A值为0 的情形先析取再合取的方式;同理,当A的值为1 的情形较少时,我们可采取先合取再析取的方式。显然,(3)式就是T 型元胞自动机R31 的迭代函数表示式,即:
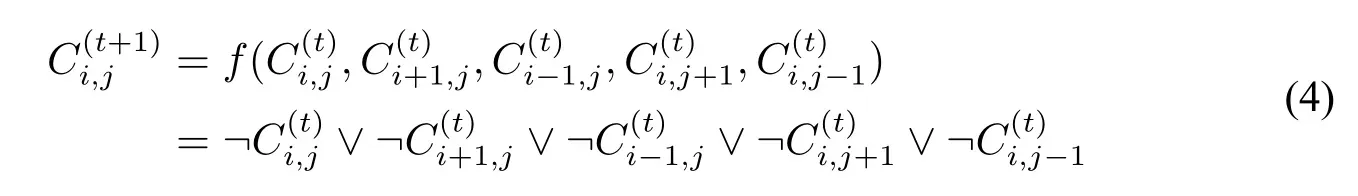
并且,无论是任意一个Rn元胞自动机,我们都可以通过这样的方法求得其逻辑表达式。那么,根据R31 的逻辑表达式,我们可以得到由其导出的自指语句集{Ci,j|i,j ∈Z},Ci,j的定义是由下列语句得到:

4 寻找不动点
我们将[9]已证明的命题([9],命题3.2)进行扩展可得,如果T 型元胞自动机的任意演化序列没有不动点,那么{Cx,y|x ∈Z,y ∈Z}是悖论的。那么,如何判断T 型元胞自动机是否有不动点,如果有的话,它的表现形式又是怎样的?T 型元胞自动机的不动点应该如何确立?文[9]为确定初等元胞自动机的不动点提出了一种树状图方法,下面把这种方法进行推广以便能够处理冯诺依曼型元胞自动机的不动点。在此,我们以R31 为例来介绍这种方法。在上一节,我们已知R31迭代规则的逻辑表达式为:

结合两种情形,为了直观,做T 型元胞自动机R31 不动点规律的树状图,如图4-1 所示。因此,综上所述,我们可以得出在以R31 为例的情况下,发现该自动机没有不动点。同理可证,在剩下的63 个T 型元胞自动机下,R1 元胞自动机也没有不动点,后续也将进一步验证。
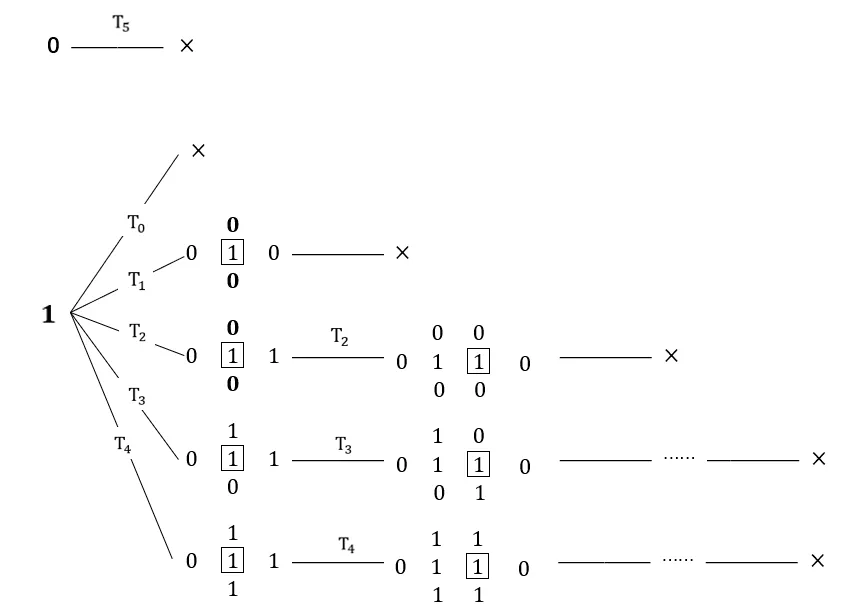
图4-1:冯诺依曼型元胞自动机R31 的不动点规律
上述以R31 为例简单地介绍了对于T 型元胞自动机的不动点,应该通过怎样的一种方法去寻找。对于没有不动点的元胞自动机,我们应用上述的方法,可以很清晰地进行相应的判断。而当对存在不动点的元胞自动机应用上述方法时,我们会发现,因为T 型元胞自动机二维空间的性质,情形复杂多变。通过笔者对T型元胞自动机的研究发现,对于满足出现不动点的情形可以通过相应的子规则进行组合构成形成不动点的全局条件。为了让读者们更加清晰的理解,以R3 元胞自动机为例,并试图通过这种方式得到获得R3 元胞自动机不动点的规律性的元胞状态。
根据图4-2 所示的寻找不动点的树状图,具体的情形分析同R31 相似,我们就不过多笔墨进行一一分析。通过图4-2,当C0,0(k)=1 时,只有T1条件才能满足,即周边元胞状态都为0 的情形,此时我们可以回到当C0,0(k)=0 的情况进行分析。当C0,0(k)=0 时,虽然通过T4、T3和T2条件,我们都能得到该状态,但在进行下一阶段时,T3和T2条件(两种分布下的其中一种情形)下,状态为0 的元胞就找不到能满足当前状态的条件,因为由图4-2 我们知道当状态为1 的元胞出现时,其周边状态必然为0,所以这两个路径下的情况时不成立的。此时在状态为0 的目标元胞下,仅有T2条件和T4条件的路径满足。而当在T4条件下时,目标元胞周边状态都变为1,此时就能全部落回C0,0(k)=1 的情形下,那么就可以得到由条件…T1-T4-T1-T4…的循环路径构成的不动点,即0、1 交替出现的元胞状态;而一旦满足该条件下的不动点,则其出现的情形必然是在全局状态下都满足该条件,也就是说在二维平面空间下都满足这个条件的R3 自动机才能出现不动点。因此,在T1-T4全局条件下,我们可以得到如图4-5(左)所示矩阵分布的不动点。同样的,显然同时满足T1→1,T4→0 的元胞自动机要存在该全局条件下分布的不动点,具体见表4-1。

图4-2:冯诺依曼型元胞自动机R3 的不动点规律

图4-3:满足冯诺依曼型元胞自动机的全局条件
根据上述方法,我们发现当存在能构成从0-1 的状态变化条件循环时,我们就可以获得一个由全局条件决定下的不动点,而满足这样要求的条件除了上面已经说明的,还有T2→1 和T3→0,其循环条件如图4-3 所示。因此,在T2→1和T3→0 组合条件下,有24个冯诺依曼型元胞自动机具有满足该全局条件下的不动点,具体见表4-1。
在前文中,我们已经通过采用确定不动点的方法,发现了在能够构成从1 到0 下的循环状态的情况下,可以得到形成不动点的全局条件。而除此之外,还有一种满足嵌套关系的全局条件能够构造不动点的全局状态,接下来将以R8 为例进行介绍。具体的不动点树状图展开方法同上述相同,如图4-4 所示。

图4-4:冯诺依曼型元胞自动机R8 的不动点规律
在T3→1 和T1→0 条件下,可以发现其元胞状态形式具有重叠部分,我们可以通过相应的嵌套,根据其重叠部分出现的规律排列,即若干个的一列(行)1 和两列(行)0 自由组合,从而形成不动点的全局状态,同样的在T3→1 和T2→0 条件下也能形成该自动机不动点的相应全局状态,即若干个的一列(行)1 和一列(行)0 自由组合。根据这两个全局条件,我们可以构造出R8 自动机的不动点,图4-5(右)为其中一种随机组合情况,根据该条件,R8 自动机有无数个不动点。

图4-5:满足冯诺依曼型元胞自动机R3(左)和R8(右)的不动点分布矩阵
同样的,在T3→1 和T1→0、T3→1 和T2→0,也分别有24个T 型元胞自动机具有满足该全局条件下的不动点,具体由下表3-9 所列。同理所得,T4→1和T1→0 以及T4→1 和T2→0 这两组组合,也能通过嵌套关系,得到相应T型元胞自动机不动点出现的组合规律,分别为若干个的两列(行)1 和两列(行)0 的自由组合及若干个的一列(行)1、一列(行)0 和一列(行)1 的自由组合,满足相对应条件的元胞自动机也由下表4-1 所列。
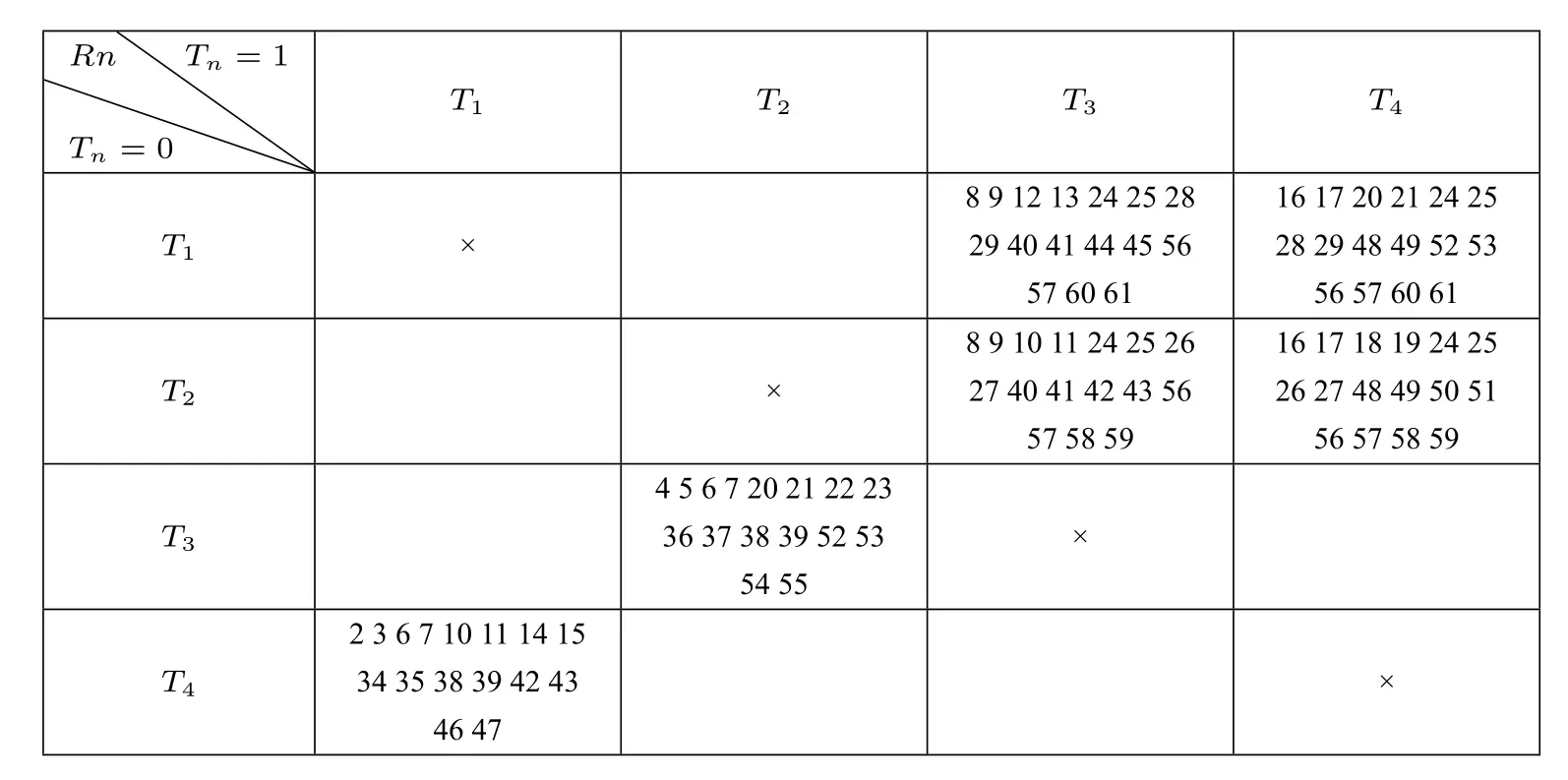
表4-1:出现不动点性质的组合规律
5 冯诺依曼型元胞自动机、说谎者悖论和Curry 悖论
由前文可知,文[9]已经证明没有不动点的元胞自动机演化序列诱导的自指集{Ci|i ∈Z}是悖论的。那么,R1 和R31 冯诺依曼型元胞自动机诱导的自指集肯定也是悖论的。在对这些没有不动点的冯诺依曼型元胞自动机进一步的分析前,我们先来看看最简单的一种语义悖论——说谎者悖论。([7])一般下列形式的语句,通常被称为说谎者悖论:

当我们对语句(7)赋值为真时,那么其表达的内容是假的,而当我们赋值为假时,其表达的内容又是真的;简而言之,无论对语句(7)赋予哪个值,都会造成自身的相互矛盾,因此这样形式的悖论,我们称之为说谎者悖论,也是广为人知的悖论之一。
当我们用γ表示语句(7)时,那么说谎者悖论可形式化为:根据古纳塔和贝尔纳普的修正理论,其修正序列不存在不动点;同时,赫兹伯格证明了这样的悖论性语句虽然不能保证收敛或具有不动点,但在修正过程稳定后会有稳定和被认为是“固定间隔”的无休止重复。([8])所以像包含说谎者悖论这样的悖论性语句,其修正序列虽然不会出现不动点,但它会出现周期型循环的变化规律,从而可以得到说谎者悖论的动态修正过程。

图5-1:冯诺依曼型元胞自动机R1 的不动点规律
同上所述,我们从假设X0开始,来对所有n ≥0 的Xn进行归纳定义:首先,我们以空集X0作为修正序列的起始值,有因此我们可以得到VX0(γ)=1。所以,有γ ∈X1。此时,我们可得显然又有VX1(γ)=0,那么,以此类推,用数学归纳法我们可以证明:当n为偶数时,VXn(γ)=1;当n为奇数时,VXn(γ)=0。将所得的说谎者悖论修正过程如下表5-1 所示:
此时,我们把目光转回没有不动点的冯诺依曼型元胞自动机,试图分析其诱导所得的自指集具备的悖论性质。让我们以R1 冯诺依曼型元胞自动机为例进行分析,获得不动点规律树状图的分析过程与第三节R31 冯诺依曼型元胞自动机相似,就不过多阐述。如图5-1 所示,显然R1 自动机没有不动点。

表5-1:说谎者悖论的修正过程

图5-2:冯诺依曼型元胞自动机R1 演化规则
我们根据R1 元胞自动机的图示化规则(如图5-2 所示),可求得其演化规则的逻辑表达式为:
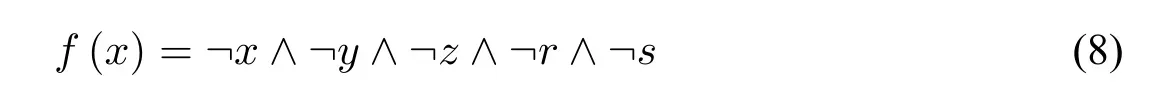
由式(8)可得,当我们对公式右边x赋值为1 时,f(x)的值为0;当我们对公式左边f(x)赋值为1 时,公式左边x的值必然为0。根据元胞自动机不动点的表达式所以有f(x)=x,与上述分析相矛盾。同时,我们可以发现这样的一个矛盾性质的R1 元胞自动机同我们说谎者悖论的性质具有同样迭代周期。无论其初始状态的分布规律如何,在经历有穷步的迭代后,总会落入0-1 的迭代周期中,而这种迭代周期恰恰也是对应着说谎者悖论的一个修正过程。这样的情况下,我们可以说R1 元胞自动机与我们的说谎者悖论的修正序列保持着一致的动态变化过程。因此,我们也可将其称作具有说谎者悖论性质的冯诺依曼型元胞自动机。
在前文中,我们已对不存在不动点的R1 的Totalistic 型冯诺依曼元胞自动机的悖论性质进行了探讨。同时,我们在第4 节中,已经证明了R31 的T 型元胞自动机也是没有不动点的,换句话说,也具有某种悖论的性质。在进行探讨之前,我们先引入Curry 悖论。
Curry 悖论首次出现在H.B.Curry 在“组合逻辑”中的悖论式组合的讨论中([1,2]),随后被Fitch 作为一种集合论悖论在其文章中出现。([3],第107-108 页)随后,Löb 根据Curry 悖论的性质,构建了其勒布定理证明的关键自指语句。([10])
Curry 悖论的语句形式,可被视为如下:
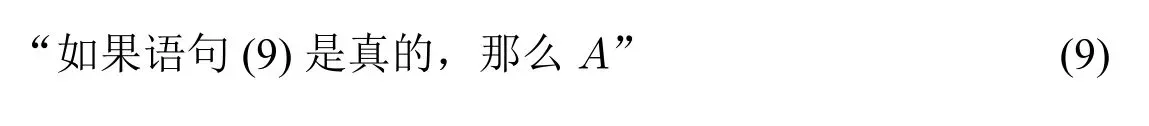
如果将B 视作语句(9),可将其形式化为:

等式左边的B仅在等式右边中B为真,A为假的条件下为假,此时,就产生了矛盾。与此同时,当等式左边为真时,无论A是什么,A都为真,这就是Löb 定理证明的关键,在此我们只关注B语句产生矛盾的情况。因此,语句B形式的悖论被称为Curry 悖论。
对于Curry 悖论,我们由公式(10)可以发现,当A为假命题时,语句B的结构等价于说谎者悖论。因此,同说谎者悖论一样,根据修正理论,我们也可以得到相应的修正序列,如表5-1 所示。

表5-1:Curry 悖论的修正过程
由第3 节,我们可得由其R31 诱导所得的自指语句集{Ci,j|i,j ∈Z},如下所示:
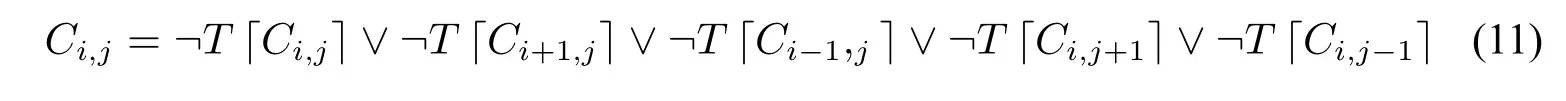
由逻辑等价替换,可得:

由公式(12)可以发现,R31 元胞自动机的自指语句形式和Curry 悖论有着异曲同工之处。即,当我们将Ci,j视为语句当作A,那么可以发现它们有着相同的形式结构。有趣的是,根据我们在第四节中已经证明的,R31 元胞自动机不存在不动点,也就是悖论的。
根据Curry 悖论的修正过程和R31 的迭代规则,我们可以发现R31 元胞自动机也有着与Curry 悖论相同的迭代周期。因此,我们可以把这样子的元胞自动机称作,具有Curry 悖论性质的元胞自动机。
6 结论
现在让我们对26个T 型元胞自动机诱导的自指语句相应的不动点形式进行分析。首先,我们已经证明了R1 和R31 元胞自动机是没有不动点的,那么现在我们就剩下62 个T 型元胞自动机。同时,我们已经知道在具有T1→1 和T4→0、T2→1 和T3→0、T3→1 和T1→0、T3→1 和T2→0、T4→1 和T1→0 以及T4→1 和T2→0 这六种组合情形之一的T 型元胞自动机可以具有无数个不动点,那么在剩下的62 个自动机中排除这六种组合的情形,就只剩下6 个T 型元胞自动机,分别为R0、R30、R32、R33、R62、R63。显然,其中R0 和R63 有且仅有唯一的不动点,且其不动点分别是0 和1。如果迭代函数具有“T5→1”或“T0→0”的元胞自动机,显然至少有一个不动点,那么R30 和R33 至少存在一个不动点;如果迭代函数具有“T5→1”和“T0→0”的元胞自动机,显然R32和R62 至少有两个不动点。通过寻找不动点的树状图方法验证可得,R30 和R33有且仅有一个不动点,而R32 和R62 有且仅有两个不动点。
根据前面对T 型元胞自动机的分析,在这我们可以根据由形式化冯诺依曼型元胞自动机的演化序列得到的不动点的特征,对26个冯诺依曼型元胞自动机进行分类,并列表如下:

表6-1:冯诺依曼型元胞自动机的分类
第一类T 型元胞自动机是没有不动点的,在其任意的初始状态下,这些元胞自动机的演化序列都不会出现不动点,这样子的T 型元胞自动机我们也可以称作悖论性的元胞自动机,其中R1 元胞自动机呈现说谎者悖论性质,而R31 与逻辑上的Curry 悖论有着相类似的结构;第二类T 型元胞自动机是有且仅有一个不动点的,即全局状态值全为0,除此之外的任意状态下该自动机都不能达到不动点的状态,例如,R0 只具有不动点0;同理,第三类T 型元胞自动机是有且仅有一个不动点的,即全局状态值全为1,除此之外的任意状态下该自动机都不能达到不动点的状态;第四类是有且仅有两个不动点的,即全局状态值全为0(或1),除此之外的任意状态下该自动机都不能达到不动点的状态;而最后一类是具有无数个不动点的冯诺依曼型元胞自动机,只要其满足上文所给出的全局条件生成的全局状态,都能形成相应的不动点。
在元胞自动机的研究中,对元胞自动机进行有规律性的分类是元胞自动机领域研究的一个重要方向,长期以来都是各领域学者的在元胞自动机研究中的热门话题。根据不同学者的研究背景,产生了许多基于不同元胞自动机性质的分类方式,其中大部分还是基于计算机科学的分类方式。例如,Wolfram 根据计算机模拟图的演化规律对元胞自动机进行分类,将所有的初等元胞自动机分成了四种类型:稳定型、周期型、混沌型和复杂型。([13])而本文主要承续了文[9]中所提出的理论思想,通过应用修正理论,从逻辑学的角度出发对总和型冯诺依曼型元胞自动机进行了分类。
本文主要从逻辑的视角出发,将Totalistic 规则的冯诺依曼型元胞自动机进行逻辑自指语句形式的表达,从而对其不动点形式以及所存在的悖论特征进行了一个相应的分类。相对于论文[9]中的初等元胞自动机,将初等元胞自动机系统扩展到二维不仅仅是因为这种扩展带来了许多涉及二维模式边界和界面行为的新现象;而更重要的是,二维元胞自动机系统作为一种平面模型,更容易用来比较现实物理系统。通过本文的研究,从逻辑的视角出发对元胞自动机进行分类,希望能够在一个更大的范围建立起元胞自动机与自指语句内在的逻辑联系,使人们能够进一步看到元胞自动机和自指语句所具有的结构相似性,从而进一步推动人们对自指语句、乃至逻辑学领域的相关的跨学科研究。

