二阶修正KROM 逻辑的表达能力与复杂性

冯世光 王克诩 赵希顺

1 引言

有穷模型论以有穷结构为主要研究对象，其发展受到了计算复杂性理论、数据库理论和形式语言的影响。1950 年B.Trakhtenbrot 证明了在有穷模型上一个公式的可满足性问题是不可判定的（[17]），标志着有穷模型论的诞生。描述复杂性理论是有穷模型论的一个分支，它从逻辑的角度对计算复杂性进行研究。计算复杂性理论关心的是解决一个问题所需要的时间和空间资源，而描述复杂性则主要研究定义一个问题所需要的最小逻辑的表达能力。判断一个结构A是否满足公式φ的复杂性有三种：(1)数据复杂性，即公式φ给定，结构A作为问题的输入；(2)表达式复杂性，即结构A给定，公式φ作为问题的输入；(3)混合复杂性，即结构A和公式φ同时作为问题的输入。

本文主要考虑数据复杂性，一般随着表达能力的增强一个逻辑的数据复杂性也会变大。例如一阶逻辑的数据复杂性在L 中，但它不能表达图的三着色问题。存在型二阶逻辑（∃SO）可以表达图的三着色问题，但它的数据复杂性是NP 完全的。在描述复杂性中用“刻画”来定义这种表达能力与数据复杂性之间的关系。称逻辑L刻画复杂性类C，则他们满足：(1)逻辑L的数据复杂性在C中；(2)复杂性类C中的问题在逻辑L中可表达。

有了刻画的概念之后，可以通过比较不同逻辑的表达能力来研究他们所刻画的复杂性类之间的关系，即如果逻辑L1刻画复杂性类C1，逻辑L2刻画复杂性类C2，则C1=C2当且仅当L1≡L2。（[5]）1974 年，R.Fagin 证明了∃SO 能够刻画NP（[6]），这一定理的证明开启了描述复杂性研究的先河。1982 年，N.Immerman 和M.Vardi 分别证明了最小固定点逻辑FO(LFP)可以在有序结构上刻画P。（[13,19]）1987 年，N.Immerman 证明了确定传递闭包逻辑FO(DTC)和传递闭包逻辑FO(TC)可以在有序结构上分别刻画L 和NL。（[14]）1989 年，S.Abiteboul 和V.Vianu 证明了部分固定点逻辑FO(PFP) 可以在有序结构上刻画PSPACE。（[1]）还有一些研究者继续从二阶逻辑的角度对描述复杂性进行了研究。J.Büchi（[2,3]）和B.Trakhtenbrot（[18]）分别独立证明了一个语言是正则的当且仅当它可以被单二阶逻辑（MSO）定义。E.Grädel 证明了二阶HORN 逻辑（SO-HORN）和二阶KROM逻辑（SO-KROM）在有序结构上分别可以刻画P 和NL。（[10,11]）S.Cook 和A.Kolokolova 提出了基于约束算术的V-Krom 逻辑，并研究了其对NL 的刻画关系。（[4]）本文作者提出了二阶修正HORN 逻辑，证明了其与FO(LFP)逻辑的等价性，并研究了对复杂性类P 的刻画关系。（[7,8]）

本文对二阶KROM 逻辑进行扩充，然后提出了二阶修正KROM 逻辑（SOKROMr），二阶扩展KROM 逻辑（SO-EKROM）和二阶扩展修正KROM 逻辑（SO-EKROMr），并对他们的表达能力和复杂性进行了研究。本文结构如下：第二节是预备知识，给出了一些基本概念和定义。第三节研究了SO-KROMr的描述复杂性，证明了在有序结构上SO-KROMr的存在型部分等价，可以刻画NL；而它的全称存在型部分可以刻画co-NP。第四节研究了二阶扩展KROM 逻辑（SO-EKROM）与二阶扩展修正KROM 逻辑（SOEKROMr）的描述复杂性，证明了SO-EKROM 与其全称存在型部分等价，他们可以在有序结构上刻画co-NP；在所有结构上，SO-EKROMr的全称存在型部分等价，也可以刻画co-NP。本文的部分结果见图1。

图1:SO-KROMr、SO-EKROM 与SO-EKROMr 的表达能力与刻画关系

2 预备知识

本文假设读者对数理逻辑和计算复杂性理论有基本的了解，相关内容可以查阅文献[5,12,16]。下面我们简单介绍本文所涉及的概念和定义。

令τ={c1,c2,...,cm,P1,P2,...,Pn}是一个词汇表，其中c1,c2,...,cm是常项符号，P1,P2,...,Pn是关系符号。一个τ-结构A具有如下形式：

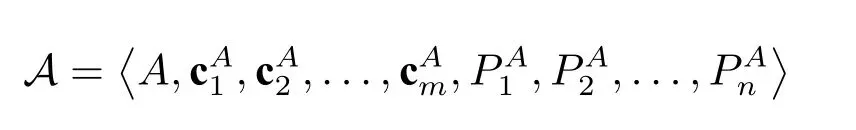
其中A是一个非空集合，是结构A的论域，分别是τ中的常项符和关系符在A上的解释(我们默认每个词汇表都包含等词“=”，并且被解释为论域中元素之间的相等关系)。在不引起歧义的情况下我们通常会省略常项和关系的上标A。我们称A是有穷结构当且仅当它的论域A是一个有限集。如无特别说明，本文中所涉及到的结构均为有穷结构。我们用符号|·|来代表一个集合的基数或者一个元组的维数，例如|A|代表论域A的基数。如果在有穷结构A上添加一个二元关系“≤”并且解释为线序关系，添加二元关系“SUCC”并解释为相对于“≤”的后继关系，添加常项“min”和“max”分别作为对最小元和最大元的解释，则称A为有序结构。

定义2.1.以τ为词汇表的二阶KROM 逻辑，记为SO-KROM(τ)，是具有下列形式的二阶公式的集合

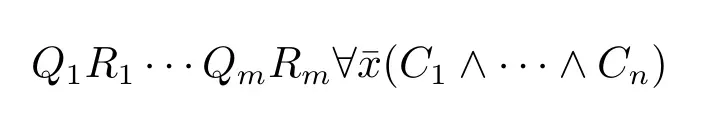
其中Qi ∈{∀,∃}，R1,...,Rm是二阶变元，C1,...,Cn是相对于R1,...,Rm的KROM 子句，即每个Cj都是一个具有如下形式的析取式

则我们称这一逻辑为二阶修正KROM 逻辑，记为SO-KROMr(τ)。

在不引起混淆时我们通常省略记号SO-KROMr(τ)中的τ，简记为SO-KROMr。我们用来分别代表SO-KROMr中型公式和型公式的集合，即公式前缀中的二阶量词分别以全称量词“∀”和存在量词“∃”开始，并且不同类型的量词一共交替k-1 次。

例1.一个有向图是强连通的当且仅当任意两点之间都有一条路径相连。图的强连通问题定义为

输入：一个有向图G=(V,E)，其中V是顶点的集合，E是边的集合。

输出：是，如果G是强连通的；否则为否。

图的强连通问题是NL 完全的，因为NL=co-NL，因此它的补也是NL 完全的。下面的公式定义了图的强连通问题的补：

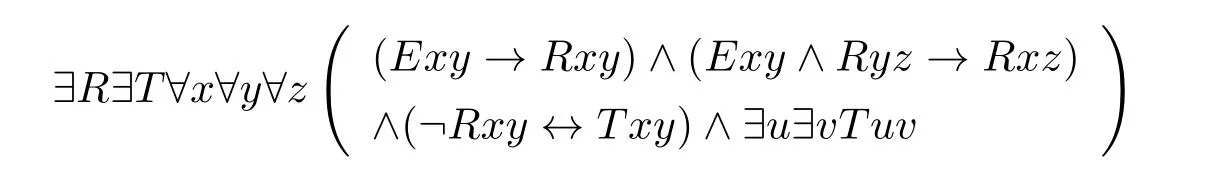
其中二阶变元R定义了图上的连通关系，T定义了R的补。若某个图满足上述公式，则必然存在两个节点a,b使得Tab为真，即a不可通达b，此图为非强连通图。

一个非强连通图的子图可能是强连通的，SO-KROM 在子结构下保持（[11]），因此图的强连通的问题的补在SO-KROM 中无法表达。例1 说明了SO-KROMr的表达能力要严格强于SO-KROM。

例2.集合{φ|φ是一个不可满足的命题CNF 公式}的判定问题是co-NP 完全的。（[16]）令词汇表τ={C,V,P,N}，其中C和V是两个一元关系符，P和N是两个二元关系符。对每个CNF 公式φ，可以用一个τ-结构Aφ=〈A,C,V,P,N〉对其进行编码（[15]），其中A是论域，对任意i,j ∈A有：Ci为真当且仅当i是一个子句；V j为真当且仅当j是一个变元；Pij为真当且仅当变元j在子句i中有正出现；Nij为真当且仅当变元j在子句i中有负出现。例如公式(p1∨p3)∧(p2∨¬p3)∧(p1∨p2)∧(¬p1)可以编码成〈{1,2,3,4},C,V,P,N〉，其中

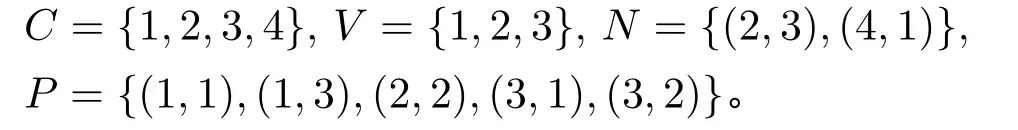
一个CNF 公式不可满足当且仅当对任意的赋值都存在一个子句使得这个子句中的所有文字在这个赋值下都为假。这一事实可以用下面的SO-KROMr公式表达：

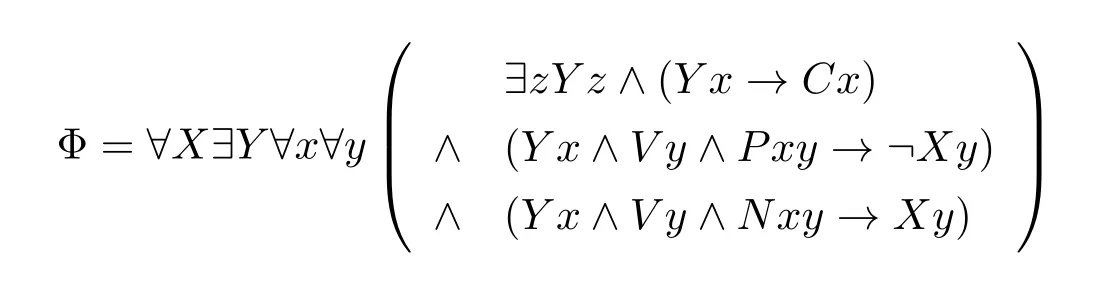
公式Φ 表达了对任意的赋值X（Xj为真当且仅当变元j在这个赋值下为真），都存在一个子句的集合Y使得其中的子句在这一赋值下都为假。容易看出对所有的CNF 公式φ，Aφ |=Φ 当且仅当φ不可满足。上面的公式Φ 是一个公式，由此可知SO-KROMr可以表达co-NP 完全的问题。

3 修正KROM 逻辑的描述复杂性

本节研究SO-KROMr的描述复杂性。由例2 可以知道SO-KROMr的数据复杂性至少是co-NP 难的。本节证明它的存在型部分的数据复杂性在NL 中，并且可以在有序结构上刻画NL；而它的全称存在型部分可以在所有结构上刻画co-NP。

命题3.1.公式都等价于一个全称型的一阶公式∀¯xφ，其中φ是一个不含量词的CNF 公式。

从命题3.1 可知如果一个SO-KROMr公式的前缀中最后的二阶量词是全称型的，则可以把通过变换把它删除，由此可以得出以下推论。

推论1.令k ≥1，如果k为奇数，则；如果k为偶数，则

引理3.1.令∃x1...∃xnφ是一个量化命题布尔公式，则它等价于如下公式

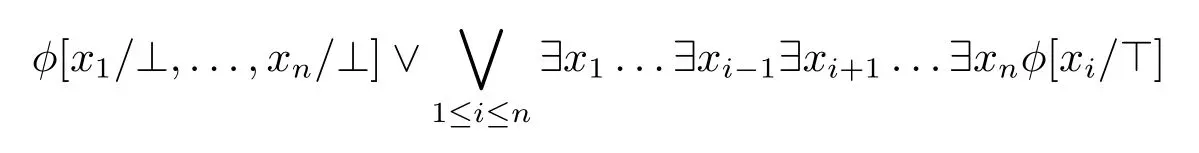
证明.∃x1...∃xnφ为真当且仅当要么所有变元x1,...,xn都为假时φ为真，要么某个xi(1≤i ≤n)为真时∃x1...∃xi-1∃xi+1...∃xnφ为真。

由例2 可以知道每个命题CNF 公式都可以编码成一个τ-结构，并且存在一个公式Φ 定义所有不可满足的CNF 公式编码成的结构。下面我们根据Ψ 构造一个τ在σ中的不含量词的解释（即用σ-结构来编码τ-结构，相关定义可参考文献[5]，第十一章第二节）

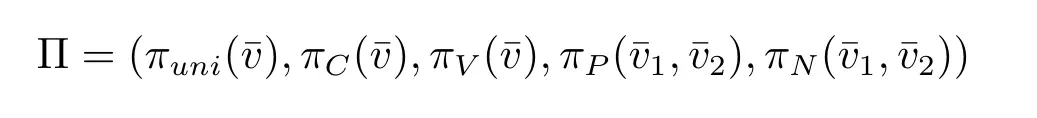
其中Π 中的公式均为不含量词的σ-公式，πuni定义了τ-结构的论域，πC,πV,πP,πN分别定义了τ-结构中的关系C,V,P,N。Π 的宽度即元组的维数且我们根据例2 中的Φ 构造出一个公式Φ-Π使得对任意至少包含两个元素的σ-结构A都有A|=Θ 当且仅当A|=Φ-Π。

公式ψ中包含的子句的数目最多为(n+1)|As|，由于把每个看成是一个命题变元，那么它包含的变元的数目最多为因此可以找到一个固定的数k使得可以用Ak中的元素对所有的子句和变元进行编码。令g=max{arity(R1),...,arity(Rm)}，k=3+max{(n+1+s),(g+m)}。定义解释Π 的宽度为定义对于Ak中的元组=(a1,a2,...,ak)，我们用前两个元素a1,a2来表示这一元组编码的是子句还是变元，即如果a1/=a2则这一元组编码子句，否则编码变元。

对于任意有穷结构A，都有一个不含量词的一阶公式φiso(x1,...,x|A|)刻画它的同构型（[5]），其中A是A的论域。所有单元素（论域中只包含一个元素）σ-结构是有限的，因此对单元素结构组成的集合都可以用一个一阶公式对其进行刻画。由此可知任何二阶公式在单元素σ-结构上都等价于一个全称型的一阶公式。假设Θ 等价于（在单元素结构上），其中φ是一个不含量词的公式。那么对任意的σ-结构A都有A|=Θ当且仅当由于全部是不含量词的公式，因此通过基本的变换操作可以将Φ-Π∨∀w¯φ转化为一个公式。

根据命题3.4 和命题3.5 我们可以得出以下结论。

定理3.3.在所有的结构上，具有相同的表达能力，可以刻画co-NP。

4 扩展修正KROM 逻辑的描述复杂性

在SO-KROM 的定义中如果我们要求每个子句都只相对于存在二阶变元是KROM 的，那么可以得到二阶扩展KROM 逻辑（SO-EKROM）。与此类似，如果在SO-KROMr的定义中要求每个子句都只相对于存在二阶变元是KROM 的，那么可以到二阶扩展修正KROM 逻辑（SO-EKROMr）。本节证明SO-EKROM 可以在有序结构上刻画co-NP，而可以在所有结构上刻画co-NP。

定义4.1.以τ为词汇表的二阶扩展KROM 逻辑，记为SO-EKROM(τ)，是下面一些二阶公式的集合

其中T1,...,Tm,R1,...,Rm是关系符号，C1,...,Cn是相对于R1,...,Rm的扩展KROM 子句，即每个Cj是一个具有如下形式的析取式

则我们称这一逻辑为二阶扩展修正KROM 逻辑，记为SO-EKROMr。

下面我们首先考虑SO-EKROM 和SO-EKROMr的数据复杂性。

命题4.1.SO-EKROM 的数据复杂性在co-NP 中。

与命题3.4 的证明类似，我们还可以得到以下结论。

命题4.2.的数据复杂性在co-NP 中。

定理4.1.在所有的结构上，可以刻画co-NP。

下面我们研究SO-EKROM 在有序结构上的描述复杂性。

根据定理4.2 和命题4.1 容易得出：

定理4.3.在有序结构上，SO-EKROM 等价于它的全称存在型部分，并且可以刻画co-NP。

5 结论