浅析中学数学数列求和的若干方法

李厚华

(重庆市荣昌中学校 402460)

数列的求和是高考、自主招生、数学竞赛的必考考点，历来都受命题者青睐.观察历届高考、自主招生、数学竞赛命题规律发现数列的求和问题，多以考查等差、等比数列的前n项和公式、错位相减法和裂项相消法为主，其次也考查倒序相加法、分组转化法、并项求和法等，且考查频率较高，是命题的热点，其中选择题、填空题、解答题都有可能出现.这就要求我们要掌握一些常用的解题方法、技巧，能根据题目条件，抓住数列的通项公式及递推公式，灵活选择数列求和的方法，做到事半功倍，快速突破.

一、公式法求和

公式法求和就是利用等差数列和等比数列前n项和公式或利用其它常见数列恒等式，直接求和的方法，理解并掌握以下公式.

1.等差数列an的前n项和公式

2.等比数列an的前n项和公式

3.常见数列恒等式

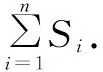
解由题意可设第n个正方形的边长为an，则这n个正方形的边长构成数列an.

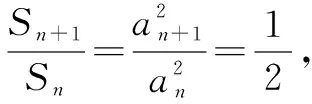
从例1解法看出利用公式法解题时，要读懂题目，挖掘出隐含的条件，并找准首项、公差、公比等基本量.

二、裂项相消法求和

1.分式裂项型

2.乘积裂项型

3.阶乘裂项型

(1)n·n!=(n+1)!-n!;

4.三角函数裂项型

5.根式裂项型

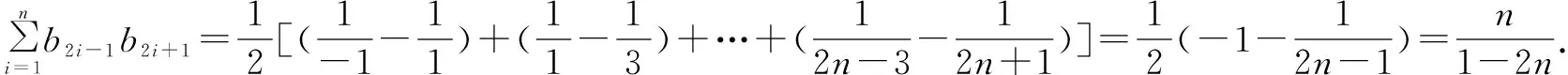
裂项相消法求和,巧在抓数列通项，根据数列通项特点，将通项裂为两项，一分为二，在求和过程中出现绝对值相同而符号相反的项，达到相互抵消的目的.

三、错位相减法求和

错位相减法求和是指数列an是等差数列，数列bn是等比数列且公比为q(q≠1)，求数列{anbn}的前n项和时，常用“乘公比，错位减”的方法，在写出Sn与qSn表达式时，应特别注意将两式“错项对齐”，相减后的未消项及相消项呈现的规律，以便于下一步准确的求出数列{anbn}的前n项和Sn.

解当n=1时，由题意得：2(a1+a2)=12a1，即a2=5a1=5.

∵数列an是等差数列，a1=1，∴d=a2-a1=5-1=4.

∴an=a1+(n-1)d=4n-3,∴bn=anp(an+3)/4=(4n-3)pn.

∴Tn=p+5p2+9p3+…+(4n-7)pn-1+(4n-3)pn,

pTn=p2+5p3+9p4+…+(4n-7)pn+(4n-3)pn+1.

两式相减得(1-p)Tn=p+4(p2+p3+p4+…+pn)-(4n-3)pn+1

=-3p+4(p+p2+p3+…+pn)-(4n-3)pn+1,

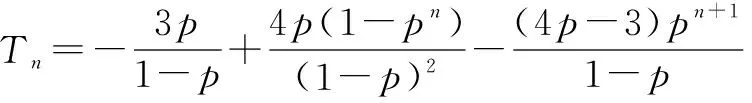
运用错位相减法求和，解题过程有一定的操作程序，容易入手，但运算量较大，要特别注意不要出错.

四、倒序相加法求和

如果一个是数列an满足am+an-m+1=a1+an，即距离首末两项“等距离”的两项之和都相等，那我们将一个数列和式倒过来写，再把它与原数列和式相加，就可以求出数列的前n项和的方法.

例4 若函数f(x)对任意x∈R都有f(2019-x)+f(x)=2成立，数列an满足：an=f(n)，n∈N*，数列an前n项和为Sn，求S2018.

解∵f(2019-x)+f(x)=2，由an=f(n)，n∈N*可得a2019-n+an=2,n∈N*，

∴S2018=a1+a2+a3+…+a2017+a2018，

S2018=a2018+a2017+a2016+…+a2+a1.

两式相加得

2S2018=(a1+a2018)+(a2+a2017)+…+(a2018+a1)=2018(a1+a2018)=2018×2,

∴S2018=2018.

通过对例4观察可发现只要一个和式满足f(a-x)+f(x)=b,均可用倒序相加法求和，倒序相加法是一种重要的思想方法.

五、分组转化求和法

已知一个数列an的通项公式是由若干个等差数列或等比数列或其它可求和的特殊数列组成，则数列an的前n项和可通过分组求和后再相加就得到原数列的和的方法.

例5 已知数列an的前n项和为Sn,且an=3n-1+(-1)n2n,n∈N*，求Sn.

解由题意可分为两组求和

Sn=a1+a2+a3+…+an

=(1+3+32+…+3n-1)+{(-2+4)+(-6+8)+…+[(-1)n-12(n-1)+(-1)n2n]}

当n为奇数时,

本题可看出分组求和法适用于解决数列通项公式可以写成an=bn+cn的形式的数列求和问题，其基本的解题技巧在于准确拆分，分组求和，从而得出原数列的前n项和.

六、并项求和法

针对一些特殊的数列采取将某些项放在一起求和，然后再求数列前n项和的方法.

例6 已知数列an的前n项和为Sn,其中a1=-1,a2=0,an-1+an+1=|an|(n≥2),求S2018.

解由an-1+an+1=|an|(n≥2),

得：an+1=|an|-an-1(n≥2).

∵a1=-1,a2=0，∴a3=1,a4=1,a5=0,a6=-1,a7=1,a8=2,a9=1,a10=-1,a11=0,a12=1,a13=1,a14=0,a15=-1,a16=1,a17=2,a18=1.

观察可知该数列从第10项开始出现循环，即an+9=an，周期T=9.

一个周期各项和为(a1+a2+…+a9)=4,

∴S2018=(a1+a2+…+a9)+(a10+a11+…+a18)+…+(a2008+…+a2016)+a2017+a2018

=224(a1+a2+…+a9)+a224×9+1+a224×9+2

=224×4+a1+a2=895.

数列中相邻两项或几项的和是同一个常数或有规律可循，可采用将这些特殊的项放在一起先求和，然后再求Sn方法.

数列求和不仅仅是数学中的数列知识的演绎，高中数学的重要内容，又是学习高等数学的基础.数列求和中不仅蕴含着丰富的数学思想方法(如方程的思想、分类讨论思想等)，更主要的是蕴含着丰富的数学解题思想方法(如公式法求和、错位相减法法求和、裂项相消法求和、倒序相加法求和、分组转化法求和、并项法求和等).这些思想方法对培养我们的阅读理解能力、运算能力和逻辑思维能力等基本能力有着不可替代的作用，在运用这些方法解决一些实际问题的过程中更多地体会数学的应用价值，同时，在解决问题的过程中也能对我们的价值观和世界观的培养有着积极的影响，不断发挥数学的教育功能，给予我们充分的探索空间.